基于融合免疫优化和遗传算法的多应急物资中心选址与调度

许伦辉，曹宇超，林培群

(华南理工大学 土木与交通学院，广东 广州 510640)

近年来，全球各类自然和社会公共突发性灾害事件频发，给社会和百姓造成了巨大的损失和困扰。社会经济受到影响，人们的生命和安全也受到了巨大的威胁，物资供应也面临着巨大的阻碍。为了降低损失，及时应对受灾区资源短缺，解决物资需求的问题，合理的应急物资中心选址及物资调度就显得尤为重要，它关系到能否及时响应灾区受灾点物资需求，保证援助效率。

应急物资网络的本质是从应急物资中心出发配送物资到受灾点的物流模式，近年来，国内外学者对于物流方面的选址问题研究成果众多。如：Yang等[1]建立了以成本和距离最小为双目标的消防站选址模型，并利用遗传算法求解了模型；王文峰等[2]以最大覆盖模型为目标，建立了多级覆盖质量要求下的设施选址模型，并设计了启发式算法进行求解；Rawls等[3]建立了应急物资储备库选址及救援物资种类决策的两阶段混合整数规划模型；李现美[4]建立了应急物资储备中心多目标多级的最大覆盖选址模型，并设计了遗传-粒子群混合算法对模型进行求解；徐重岐等[5]提出了一种基于混合整数规划模型的应急物流配送中心选址方法；赵仁辉等[6]针对单一指派约束和容量约束，以总成本费用最小为目标建立了一种基于改进蚁群算法与GIS的配送中心选址方法；Ai等[7]建立了海上救援应急物资储备库与应急救援船舶的资源配置模型，并用遗传算法求解了该模型；张敏等[8]建立了基于失效情形的应急设施选址评估指标体系并运用数据包络法对应急设施选址的合理性进行了评价；冯舰锐等[9]基于运筹学中多目标优化理论，并引入了多影响因素权重因子，建立了应急物资中心选址问题的优化模型；宋英华等[10]构建了以最小配送时间和成本为目标函数，考虑了动态环境下的应急物资中心快速选址模型；Wang等[11]基于局部分支和粒子群优化的方法提出了一种随机规划模型，考虑具体受损场景以及引入抗震能力，确定灾难现场应急仓库的选址和规模。文献[1-11]只研究了应急中心的选址，并没有进一步设计后续的物资调配方案。李进等[12]对于多种类物资分类调度建立了对应多受灾点的调度模型；刘长石等[13]考虑了应急物资配送的具体需求量和时间效率问题，建立了物资由多个应急物流中心到多个需求点的应急物流模式并且建立了总运达时间最短与总配送成本最小的多目标模型；朱洪利等[14]针对地震等突发事件发生时应急物资需求存在动态变化的特点，提出了两阶段应急资源调度模型；Wang等[15]提出了以最短时间，最少成本多目标的二维优化模型，应用理想点算法来解决应急物资的调运问题；赵振亚等[16]建立了基于最小风险路径的应急物资调度配送方案；孙欣欣等[17]构建了基于运输时间最短、物资储备库最少的多目标应急物资调度计算模型，利用遗传算法进行调度方案求解；李巧茹等[18]提出一种考虑灾后道路可靠性的多目标优化应急调度模型，以车辆行驶时间最小、行驶路径可靠度最大和系统物资未满足度最小为目标函数，采用改进遗传算法进行求解。虽然文献[12-18]在物资调度和路径规划方面给出了解决方案，但没有给出该情景下如何进行应急物资配送中心选址的方案。少数学者研究了选址-调度一体化问题。Caunhye等[19]建立了物资需求和设施状态不确定性条件下的两阶段的选址路径模型；Liu等[20]结合动态规划的车辆运输路径分配算法和基于蚁群优化的灾区供应序列自学习算法，建立了考虑物资需求和车辆数量不断变化的应急物资调度模型；曲冲冲等[21]基于在灾区实际状况，针对应急环境的动态性，建立了应急物资配送中心选址与运输配送路径优化模型，解决了多目标动态救援问题；许可等[22]建立了考虑物资供应约束以及转运平衡约束的多目标优化选址调度模型，使用带惯性权重的离散二进制粒子群算法对模型进行求解；姚红云等[23]基于模糊层次分析法构建了应急物资中心选址模型，并建立了灾害过程中应急物资配送路径优化模型。

可以看出，应急物资中心的选址与物资调度配置问题是整个应急物流网络的2个重要问题，多数学者是从单一角度将2个问题分开或看成2个阶段研究；少数学者虽然考虑了一体化研究，但解决方案存在改进空间。在求解该类最优问题时常采用动态规划算法、启发式算法或遗传算法等智能优化算法。动态规划算法存在着耗时长、效率低的缺点；启发式算法的精确程度往往较差；标准的遗传算法以及粒子群算法往往存在容易陷于局部最优或收敛速度较慢的缺点[24-25]。

由此，本文针对应急物资中心选址与多目标点调度问题，设计了基于免疫优化算法选址和基于多层编码遗传算法调度的融合算法。免疫优化算法可通过自身调节机制[26]，保证个体多样性，避免陷入局部解；多层编码遗传算法通过改变编码方式，构建双层染色体分别表示供应方和需求方，解决此类多目标问题，融合建立了中心选址-调度一体化解决方案。

1 应急物资中心选址和调度模型

1.1 问题描述

灾害发生后，为了响应物资需求，不仅需要考虑应急物资中心至受灾区域的距离成本，而且还需要结合不同物资种类，物资需求量的运输成本进行综合考虑，选出合理的应急物资中心地址，确定最优的物资调度配送方案，以保证好各物资中心的应急物资能够以最低的成本满足受灾点的需求，保证救援效率，减少资源浪费，获得系统全局的最优方案。问题描述如图1所示。

图1 应急中心选址-调度示意Fig. 1 Emergency center site selection and dispatching diagram

1.2 应急物资中心选址模型

应急物资中心的选址建立在3个假设条件上：

1)外界补充物资足够支持任意配送需求，且应急物资中心的容纳量默认可以满足配送需求。某一物资中心的调度目标需要在其配送辐射范围之内。

2)每个应急中心物资种类齐全，一个需求点只由一个物资中心即可满足相应需求。

3)应急物资中心与需求点间的成本评估考虑综合代价，即综合考虑距离和运输成本[27]。如式(7)所示。

在3个假设的基础上建立选址模型，模型满足建立M个物资中心，以供应满足N个需求点的物资需求。M⊂N，即物资中心以需求库中的点进行建立，选为物资中心的区域可满足供应自己区域的需求，并且可以为其他非物资中心的需求点配送物资。目标函数是使物资中心到其余需求点的综合代价值Fs最小，目标函数为

(1)

约束条件为：

(2)

Zi,j≤hj，i∈N，j∈Mi，

(3)

(4)

Zi,j,hj∈0 或 1，i∈N，j∈Mi，

(5)

di,j≤s。

(6)

式中：N表示所有需求点的集合；i表示第i个目标需求点；Mi表示能辐射到i点的应急物资中心集合；j表示第j个物资中心；Zi,j用0和1表示需求点和物资中心是否存在配送关系，若i点由j中心供应，则Zi,j=1，反之为0；hj采用0和1表示j点是否已被选为配送中心，hj=1表示被选为配送中心，反之为0；di,j表示i点与j中心间的距离；s表示辐射范围。

式(2)表示每个需求点仅由一个物资中心提供物资即可；式(3)表示需求点只能被设为物资中心的点供应；式(4)表示建立的物资中心数目为M；式(6)表示物资配送需在辐射范围内。

下面计算综合代价。综合代价分别考虑了物资配送的距离成本和运输成本，计算公式为

w(d,p,g)=pd+dηg，

(7)

式中：pd表示配送的距离成本；dηg表示运输成本。其中距离成本在配送路径选择中，主要需要考虑道路的通畅度，即拥堵程度会影响距离成本和总体耗时，因此对出行距离d添加了交通拥堵系数p作为距离成本系数。在运输成本中，η表示运输成本中需求物资单位需求量的成本换算系数，g表示物资需求量。

表1 速度-交通拥堵系数对照

(8)

2)运输成本中需求物资单位需求量的成本换算系数η的取值结合具体运送的物资，根据不同种类物资在运输途中的易损程度，通过经验函数及相关统计数据确定。

1.3 多目标物资调度模型

多目标物资中心调度问题的本质就是合理安排配送路线，使得全局总代价最小，基于物资中心选址模型，受灾区中有M个物资中心，总共要给N个需求受灾点配送，设第m个物资中心要向Lm(m=1,2,…,M)个需求点送货，第m个物资中心有Km辆配送车，车辆限载量Qm,k(k=1,2,…,Km)，其配送的最大行驶距离为Dm,k。第m个物资中心服务的第i个需求点的货物需求量为qm，i(i=1,2,…,Lm)，该物资中心到第i个需求点的综合代价为wm，i(m=1,2,…,M;i=1,2,…Lm)，再设nm，k为第m个物资中心中第k辆车配送的需求商数(nm，k=0表示未使用第k辆车)，rm，k，i表示物资中心m使用第k辆车为需求点i运送物资。若以全局综合代价最小为目标函数Ft，则调度模型为：

(9)

(10)

s≤Dm，k，

(11)

(12)

(13)

(14)

式(9)～(14)中：wrm，k，i表示物资中心m使用第k辆车为需求点i运送物资的综合代价值；qm，rm，k，i表示物资中心m使用第k辆车为需求点i运送的物资量。式(10)保证配送量能满足需求量；式(11)保证车辆可送达距离在物资中心辐射范围内；式(12)表明单一物资中心配送需求点数不超过总需求点数；式(13)表明所有需求点均得到供应；式(14)表示车辆状态，当第k辆车参加了配送任务则取fsign(nm，k)=1，反之取fsign(nm，k)=0。

2 融合免疫优化和多层编码遗传算法设计

免疫优化算法和遗传算法的本质都是从群体中选出优质个体。二者的算法步骤相似，由“初始种群产生→评价标准计算→种群间个体信息交换→新种群产生”这一循环过程，最终以较大的概率获得问题的最优解。

2.1 基于免疫优化算法的物资中心选址

免疫优化算法利用免疫系统产生并保持种群的多样性，对于存在多峰值的函数能避免陷入局部循环，最终可求得全局最优解。免疫算法流程如图2所示。

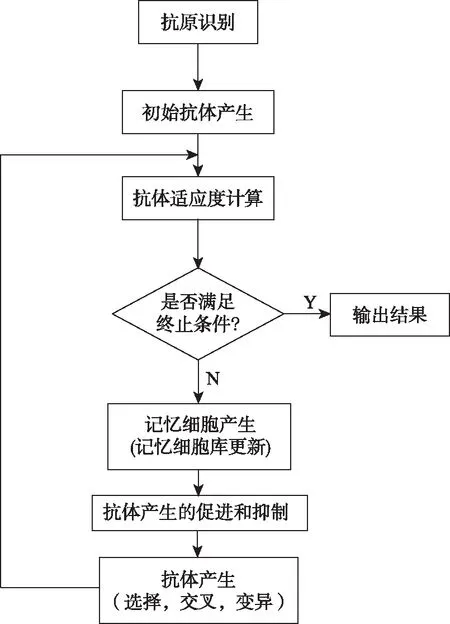
图2 免疫优化算法流程Fig. 2 Immune optimization algorithm flowchart

2.1.1 生成初始抗体群

根据候选可建立应急物资中心的区域点信息，生成初始抗体种群。设需要建立的物资中心数目为M，则选址方案生成一个长度为M的抗体[m1,m2,…,mM]。

2.1.2 解的评价

①抗体与抗原间的亲和度

描述抗体对抗原的识别程度，根据物资中心与需求点之间的关系定义亲和度函数A。

(15)

式中：Fs为选址模型中的目标函数；Ppun是惩罚函数；C是一个趋近于正无穷的数。

②抗体与抗体间的亲和度

描述抗体之间的相似程度。采用R位连续方法来计算抗体间的亲和度。

(16)

式中：ki,j表示抗体i与j中相同的位数；M表示抗体长度。如抗体[1 5 8 21 27]与抗体[2 4 8 19 27]中，有2个位数相同，则抗体间的亲和度为Si,j为0.4。

数据传输层通过与采集层和数据处理层的上下连接，通过通信网络进行信息传输，为系统提供基础设施服务。传输层由无线传感网、有线网、互联网及各种私有网络组成，在数据采集层各传感器和数据处理层之间起到纽带和桥梁作用，负责将获取的传感器感知信息，经过互联网或私有网络，安全可靠地传输到上层进行数据分析，然后根据不同的应用需求进行数据的交互与处理。该系统中主要采用蓝牙、3G/4G 移动网络和局域网络等进行数据的传输与通信。

③抗体浓度

表示满足亲和度阈值T的抗体占抗体总数的比例。

(17)

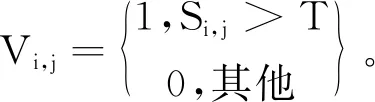
④期望繁殖概率

在一个种群中，个体的期望繁殖概率由抗体间的亲和度A和抗体浓度Cv决定。

(18)

式中α是比例系数。当个体适应度越高时，期望繁殖概率越大；当个体浓度越小时，期望繁殖概率越大。这种方式有利于选择适应度高的个体，同时抑制浓度高的个体，保证了个体多样性。

本文采取精英保留策略进行再优化，在每次更新记忆库时，先将与抗原亲和度最高的个体按比例选取一部分存入记忆库，再按照期望繁殖概率递减，从高到低将剩余个体存入记忆库，避免由于出现高浓度抑制导致最优解的丢失。

2.1.3 免疫操作

①选择：采用轮盘赌法根据式(18)的概率进行选择。即抗体被选中的概率与其期望繁殖概率成正比。

②交叉：采用随机选择交叉位置进行交叉。即随机选取2个抗体，并取出每个抗体的前M/4位，然后随机选择交叉位置进行同等长度序列的交叉。

③变异：采用随机选择变异位进行变异。变异算子首先从种群中随机选取某个抗体作为变异个体，然后选择变异位置pos1和pos2，将个体中pos1和pos2位置序列对换完成变异。

2.2 基于多层编码遗传算法的调度策略

对于应急物资调配中多目标中心对多目标需求点的问题，一般遗传算法一个单层染色体难以准确表达问题的解。本文在传统遗传算法的基础上，结合物资中心-需求点多目标调度的情景，将一般的单个单层染色体编码模式改进为双层编码，通过把个体分为两层，定义每层编码分别表示物资中心和需求点，完整表达了问题的多项参数，可获得最终的最优解。

2.2.1 基于双层编码的模式

基于每个物资中心物资种类齐全的背景，采用双层整数排列的编码方法。对于M个物资中心，N个需求点的多目标问题，染色体的第1层表示单次运送中物资需求点排列；第2层表示对应配送物资的物资中心点排列。例如N为4，M为3的染色体如图3所示。其表示物资中心1→需求点1和3；物资中心2→需求点2；物资中心3→需求点4。

图3 N=4且M=3的染色体

2.2.2 种群初始化

基于已知的需求点信息和免疫优化算法中生成的物资中心点信息，排列组合生成随机的初始种群。

2.2.3 适应度计算

设染色体的适应度值根据综合代价进行评价，计算公式为

ffit(i，j)=wi,jCi,j。

(19)

2.2.4 选择操作

选择操作采用轮盘赌法选择适应度较好的染色体，个体选择概率为：

FFit(i,j)=1/ffit(i,j)。

(20)

2.2.5 交叉操作

采用随机选择交叉位置进行交叉。与一般交叉不同的是，2个双层染色体之间，对应编码层之间的基因才可进行交叉，并计算交叉操作后新染色体的适应度值。

2.2.6 变异操作

采用随机选择变异位进行变异。与一般变异不同的是，双层染色体中，同层编码之间的基因才可进行变异，即每层独立的选择pos1和pos2位置的基因进行对换变异，并计算变异操作后新染色体的适应度值。

3 算例分析

3.1 问题背景

2020年，我国面临严峻的新型冠状病毒疫情的灾害，世界卫生组织(WHO)宣布，将新型冠状病毒疫情列为国际关注的突发公共卫生事件。本文以湖北省新型冠状病毒疫情受灾需求为背景，结合国家卫健委某日公布的地区-病人数据，根据当地病人数量正比于应急物资需求量的假设，模拟当地应急物资需求案例。如表2所示。

表2 受灾地区病人-物资需求量

3.2 应急物资中心选址

根据湖北省的地图，按比例尺构建如图4所示的坐标系，并标记受灾需求点的坐标信息。

图4 湖北省疫情受灾点信息Fig. 4 Information on the affected areas in Hubei Province

假设物资调配均采用陆运，且各地交通可达性一致，物资种类均为应急物资且在运输过程中受损度一致，取η=0.3。湖北省各地坐标-需求物资的运输成本信息如表3所示。选定17个城市的坐标信息，需要从其中选择6个城市设立为应急物资中心，其中选为应急物资中心的地址可直接为当地提供物资，满足当地需求。设定种群规模为50，迭代次数为50，交叉概率为0.5，变异概率为0.4，多样性评价参数为0.95，应用免疫优化算法确定最优的应急物资中心选址。

表3 受灾地区病人-物资需求量

通过免疫优化算法，得到随迭代次数增加而收敛的曲线如图5所示，可以看到在迭代次数10次左右出现收敛；得到物资中心选址方案如图6所示，其中方框表示应急物资中心设立点，圆圈表示其余的受灾物资需求点。

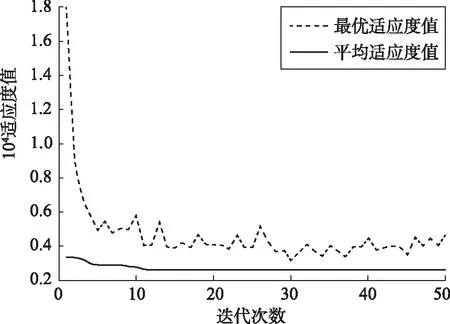
图5 免疫算法收敛曲线Fig. 5 Convergence Curve of Immune Algorithm

图6 免疫优化算法物资中心选址方案Fig. 6 Location plan of material center based on immune optimization algorithm

3.3 应急物资调配方案

根据应急物资中心的选址结果，武汉、孝感、黄冈、鄂州、荆州、襄阳6地作为物资中心，结合物资中心与其余各需求点间的距离信息、需求量信息综合得出每个物资中心配送给其余各受灾需求点物资的综合代价值，如表4所示。第1列是除了选为物资中心点外其余各需求点位置；第1行是6个被选为物资中心的点位置；表中数据是各物资中心分别到余下各需求点的运输综合代价值(选为应急中心地址的需求点默认由当地供应物资可满足需求)。假设各路段疫情期间为物资车辆保持道路畅通，道路拥堵系数p=1。运往各地物资的单位距离运输成本代价ηgj的值见表3。

表4 物资中心-受灾需求点综合运输代价值

以武汉—随州为例，综合代价的计算过程为

w武汉—随州(d武汉—随州,g随州)=d+dηg=2.8d=414.409 5≈414。

(21)

应用多层编码的遗传算法，分类为每个物资中心单次配送车辆数目无上限的情景和每个物资中心单次运输车辆数目有限制且最大值Km=2的情景进行分析。参数设种群数目为60，迭代次数为100，交叉概率为0.8，变异概率为0.6，目标是获得全局综合代价值最小的物资调度配送方案。

情景1每个物资中心单次配送车辆数目无上限。情景1的收敛曲线如图7所示，在迭代10次左右出现收敛，最优调度方案如图8所示。图中102表示由物资中心2(孝感)为需求点1(随州)运送物资，系统运输综合代价为纵坐标值283。该调度方案可以获得全局最优的结果，且目标值物资配送中心的系统运输综合代价最优，为1 908。情境1下最终形成的选址-调度方案如图9所示。

图7 情景1的调度方案迭代次数Fig. 7 Iterations of the scheduling scheme for scenario 1

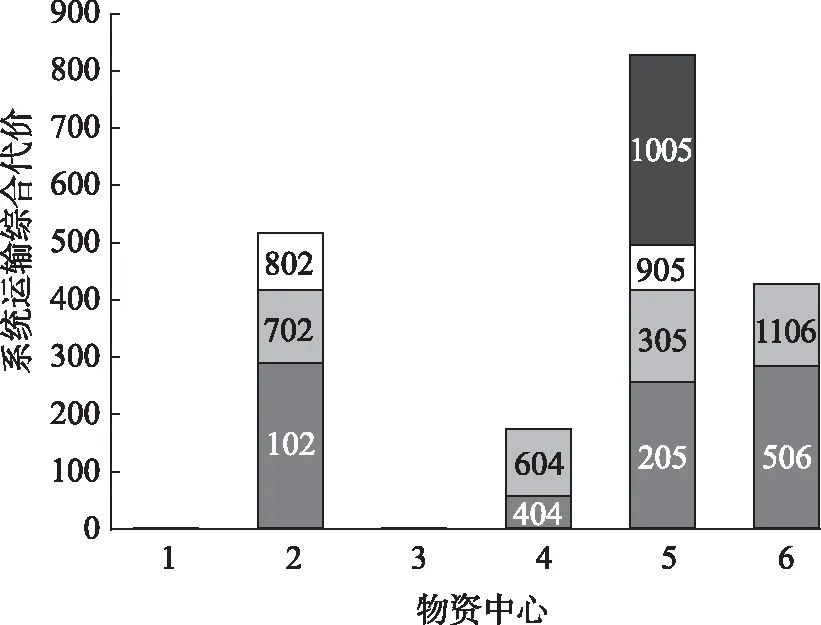
图8 情景1的调度方案甘特示意Fig. 8 Gantt diagram of scheduling scheme for scenario 1

图9 情景1的最终选址调度方案Fig. 9 Final location scheduling scheme diagram for scenario 1

情景2每个物资中心单次运输车辆数目有限制且最大值Km=2。情景2的收敛曲线如图10所示，最优调度方案如图11所示。该调度方案可以获得全局最优的结果，目标值物资配送中心的系统运输综合代价最优，为2 314。情境2下最终形成的选址-调度方案如图12所示。

图10 情景2的调度方案迭代次数Fig. 10 Scheduling scheme iterations graph for scenario 2

图11 情景2的调度方案甘特示意Fig. 11 Gantt diagram of scheduling scheme for scenario 2

图12 情景2的最终选址调度方案Fig. 12 Final location scheduling scheme diagram for scenario 2

结合案例，与其他常用于解决这两类问题的智能算法做比较，得到的对比结果如表5所示。

表5 不同算法实验性能的结果

从结果分析可以看出，本文针对这两类问题采用的免疫优化遗传算法和多层编码的遗传算法均可以获得全局最优解并且具有更高的求解效率。通过二者融合的算法能够得到一套合理的选址-调度方案。

4 结论

本文对于灾害环境下的援助提出了一套应急物资中心选址-调度配送一体化的解决方案，首先论述了中心选址问题和多目标对多目标的调度配送问题，构建了相应的数学模型，并建立了基于综合代价的成本评估模式。然后选择了免疫优化算法和改进的多层编码遗传算法分别解决中心选址和调度配送问题，并论述了算法的优势。免疫优化算法利用其多样性，增强了全局中的搜索能力而不会陷入局部解；遗传算法本身基于启发式搜索，并且具备快速随机搜索能力，针对物资调配问题改进的多层编码遗传算法能更具针对性地解决多目标-多目标的问题。基于以上优势，结合具体问题分别进行了改进算法步骤的设计。最后以湖北省新型冠状病毒疫情下的受灾需求援助作为背景，采用融合免疫优化算法和改进的多层编码遗传算法的方式建立了一套合理且高效的应急物资中心选址-物资调度配送的一体化解决方案，并且与其他常用的智能算法相比，论证了本文的方法能获得全局最优解并且保持较高的搜索效率，为灾害状况下的应急物资处置提供了高效可行的方案。