基于大数据的不确定交通流实时分配研究*

苏 兵，邵艳君，姬 浩，陈金鑫，张 娟，LIN Guohui

(1.西安工业大学 经济管理学院，西安 710021;2.阿尔贝塔大学 计算机科学系，加拿大 埃德蒙顿T6G 2E8;3. 陕西高校军民融合科技创新研究中心，西安 710021)

交通网络的用户均衡指所有出行者在完全理性的情况下独立做出令自身出行费用最小的决策，使得网络流量分布时无人能够通过单方面改变自己的路径降低自身的费用[1]。现有基于用户均衡的交通流实时分配，一类假设实时交通流量确定，构建基于变分不等式的用户均衡模型等方法[2-3]。另一类假设实时交通流量不确定，或为随机化交通流量，将其转化为静态问题进行处理[4-5]；假设实时交通流量变化不具有任何规律，采用在线理论与方法设计基于用户均衡的在线策略[6-9]，证明策略的竞争比[10-11]。在实际中交通流分配是一个由出行者参与且不断变化的能动过程，出行者无法获取确定的或统计意义下的交通流量，通常可以采用大数据分析的方法预判未来交通量从而进行路径选择。“车联网”技术使得所有的交通流量以数据的形式实时记录，“交通大数据”即由这些数据串联融合形成，因此，基于交通大数据预测未来交通流量进行交通流分配，从而减少每个出行者出行费用是研究关注的重点问题。现有基于交通大数据的交通流预测大多以提高交通流预测准确度为目标，建立单一预测模型反应时间长、受外界干扰大[12-13]；最优权重组合预测模型中各模型预测值权重的设定受预测人的主观影响较大[14-15]，未将交通流预测结果贡献于交通流的有效分配上。

本文考虑实际中未来交通流量无法获知的情形，针对城市路网起始节点择路去目的地节点的交通流分配问题，基于出行者均根据费用最小原则选择各自出行路径，采用多元概率比较回归(Probit)模型计算时间段T内到达起始节点的当前交通流量大数据，选取适用于不确定交通流预测的非参数回归模型、卡尔曼(Kalman)滤波模型和神经网络模型建立贝叶斯组合预测模型，预测下一个时间段T内到达出发节点的交通流量，在此基础上，采用在线理论与方法，以达到用户均衡为目标设计贝叶斯在线用户均衡(Bayesian Online User Equilibrium,BOUE)策略，分析策略在该路段通行能力受限时不同形式路阻函数下的竞争比，并分析策略执行效果。

1 问题描述和基本假设

le=le(re)为路阻函数，用来度量e上流量为re时的通行费用，路段的通行费用l(re)与流量成正比。任意交通流量re的总通行费用可以表示为

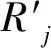
该问题符合不确定性和序贯决策过程的在线问题特征，可以采用在线理论与方法来解决，所设计在线策略下的出行费用与对应离线问题最优费用的比值越接近于1，证明策略的性能越好[7]。

为了便于分析，提出假设为

1) 出行者均选择自己认为出行费用最少的路径出行；

2) 交通流量任意可分配；

3) 出行者选择好路径后不再改变路径；

4) 把以出行者为单位的出行量转化为以用户为单位的交通流量。

2 策略及其竞争分析

出行者通过大数据分析的方法对未来交通量进行预测后主观选择出行费用最小的路径，采用Probit方法计算当前时间段内到达出发节点的交通流量数据，然后根据每个出行者出行时间不同导致交通流量在不同时间段到达节点O波动很大的特征，选取适用于预测不确定交通流量的非参数回归模型、Kalman滤波模型和神经网络模型建立贝叶斯组合预测模型来预测未来时间段内的交通流量，进一步设计策略，并对路段通行能力受限时策略的执行效果进行分析。

2.1 基于大数据的节点O的不确定交通流量计算

根据用户均衡原则，即所有出行者在完全理性情况下独立做出令自身出行费用最小的决策，计算当前到达的交通流量，在此基础上建立贝叶斯组合预测模型计算未来到达路网节点O的交通流量，计算过程如下。

1)当前时间段到达节点O的交通流量计算

给出时间点序列t0,t1,…,ti-1,ti,ti+1,…,[ti-1,ti]为任意一个时间段，T为某个时间段的长度,rPsj(ti)表示时间段[ti-1,ti]内到达节点O的交通流量，如图1所示。

图1 每个时间段到达节点O的流量图(min)Fig.1 Traffic flow at Node O during each time period (min)

用Probit方法计算第i个时间段[ti-1,ti]内到达节点O的交通流量为rPsj(ti)。

假定任一路段的通行费用满足正态分布，则出行者选择通行费用最小路径的概率为

(1)

求解上述模型，可获得每个时间段到达路网节点O的当前交通流量数据。

2)下一时间段到达节点O的交通流量预测

为减小预测误差，克服单项预测模型反应能力差、受外界干扰大的缺陷，基于交通流量大数据并结合贝叶斯组合模型对未来交通流量进行预测，选取适用于预测不确定交通流的非参数回归模型、Kalman滤波模型和神经网络模型。其中，神经网络模型能根据实时交通流量的变化自动调整预测精度；Kalman滤波模型的预测误差与时间段长度T的变化基本无关；非参数回归模型操作方便，可预测每个时间段内不同路段上的交通流量，且预测误差分布均衡。

由于受到路段通行能力的限制，有

pkrPsj(ti)=

(2)

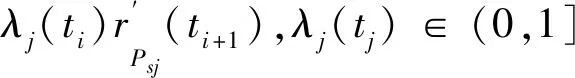
设计在线策略对可分配的交通量进行实时分配如下。

2.2 BOUE策略设计

BOUE策略下的交通流量分配如图2所示。

光伏发电系统通过光热转换，以及热电转换，将太阳能转变为电能，核心组件为太阳能电池、电容器、控制单元等。当半导体电池被太阳光照射之后，由伏特效应产生电能，并且存储至太阳能电池之中，再结合蓄电池控制器、逆变器等装置，光伏发电系统就能够实现对充电放电、交流直流转变的控制[1]。

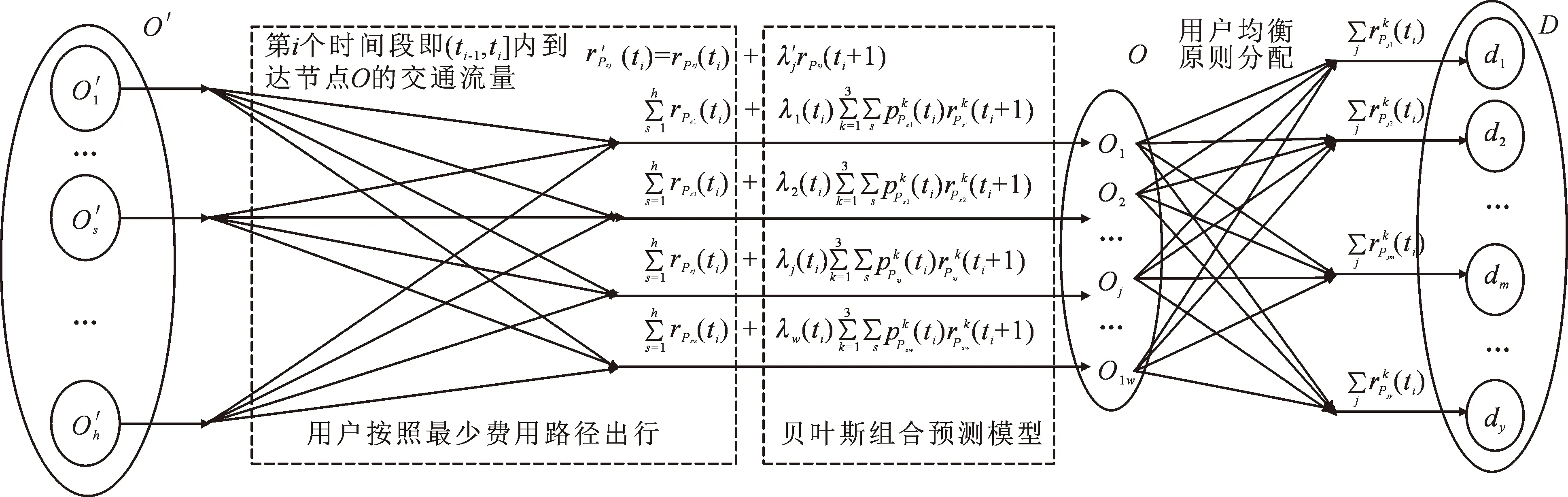
图2 贝叶斯在线用户均衡策略分配交通流量图Fig.2 Traffic flow distribution by Bayesian online user equilibrium strategy

2.3 策略竞争比分析

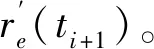
情形1 到达起始节点的当前交通流量均大于路段最大通行能力

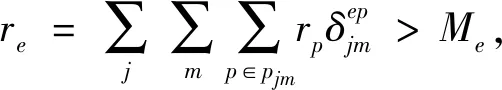
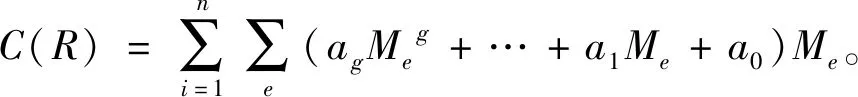
在情形1下，在线策略的竞争比与路阻函数的形式无关，所有出行者的出行费用等于对应离线问题的最优费用。

情形2 起始节点的当前交通流量大于路段最大通行能力的同时，到达路段起始节点的当前交通流量小于等于路段最大通行能力。

按照路阻函数的不同形式将情形2分为情形2.1和情形2.2，并讨论这两个子情形下BOUE策略的竞争比。

情形2.1 路阻函数为非负非递减线性函数。

路阻函数为线性函数时，BOUE策略下出行者的出行费用为

(3)

(4)

令α=maxαi,pjm，β=maxβi,pjm，λ=maxi,pjm，i=1,2,…,n-1，j=1,2,…，w,m=1,2,…,y，结合式(4)可得

整理可得

且γi,δi之间互斥，当第i个时间段的交通流量到达时满足γi+ηi=1。

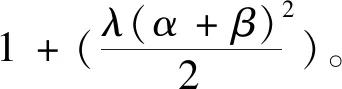
情形2.2 路阻函数是系数非负非递减且为次幂的多项式函数。

路阻函数为g次幂的多项式函数时，出行者的出行费用为

←(agrg+…+a1r+a0)]dr。

(5)

与式(3)的处理方法类似，将式(5)改写为

←(agrg+…+a1r+a0)]dr。

(6)

令α=maxαi,pjm,β=maxβi,pjm,λ=maxλi,pjm,i=1,2,…,n-1,j=1,2,…,w,m=1,2,…,y，结合式(6)可得

←(agrg+…+a1r+a0)]dr。

整理可得

←(agrg+…+a1r+a0)dr]<

因此给出定理1。

定理1 针对一个长度为T的连续时间段内到达路网出发节点的交通流量，在re(ti)>me的情形下，BOUE策略的竞争比为1；存在到达路段起始节点的当前交通流量re(ti)≤me且存在到达路段起始节点的当前到达交通流量re(ti)>me的情形下，当路阻函数le是非负非递减的线性函数时，BOUE策略的竞争比为1+(λ(α+β)/2)2；当路阻函数le是非负非递减且为g次幂的多项式函数时，BOUE策略的竞争比为1+(λ(α+β)/2)g+1，其中α=maxαi,pim，β=maxβi,pim，λ=maxλi,pim，i=1,2,…,n-1，j=1,2,…,w,m=1,2,…,y。

3 结 语

为实现每个出行者的出行费用尽可能少且不能通过单方面改变路径来进一步降低自身出行费用的目标，文中通过大数据分析的方法计算n个长度为T的连续时间段内到达路网节点O择路去路网节点D的交通流量，设计BOUE策略进行实时交通流分配，即将当前时间段到达出发节点的实际交通流量和下一时间段到达出发节点的预测交通流量一起分配到交通网络上，对策略竞争比的分析，结果表明，该策略在路段通行能力受限时不同形式路阻函数下的执行效果较好。其中，在路段通行能力受限、存在到达路段起始节点的当前交通流量re(ti)≤me且存在到达路段起始节点的当前到达交通流量re(ti)>me的情形下，当路阻函数为线性函数时BOUE策略的竞争比为1+(λ(α+β)/2)2，当路阻函数为g次幂的多项式函数时BOUE策略的竞争比为1+(λ(α+β)/2)g+1。研究结果表明，在未来交通流量不确定的基础上，结合大数据分析的方法，采用BOUE策略进行实时交通流分配可为交通管理部门指挥疏导交通流和出行者出行的实时路径选择提供有效理论依据。