虚拟多触角探测的高超声速滑翔飞行器再入机动制导
高杨,蔡光斌,2,*,徐慧,杨小冈,张胜修
1.火箭军工程大学 导弹工程学院,西安 710025 2.西北工业大学 航天学院,西安 710072
近年来,高超声速滑翔飞行器的再入机动制导过程受到各个军工大国的高度关注,其制导性能也是各大科研机构研究的重点[1-8]。高超声速滑翔飞行器一般以一定的弹道为基础在再入阶段进行制导,制导过程中受到多种约束的限制,除去飞行任务限定的始末端点约束外,还有传统路径约束和空间约束。
传统路径约束包括热流率约束、动压约束和过载约束。在离线的状态下,目前已经有很多成熟的算法,其中,以高斯伪谱法为代表的数值优化求解方法已渐趋成熟,可以在满足以上约束条件的情况下,求解出不同优化目标的最优轨迹[9-13]。另一部分学者针对准平衡条件的“软约束”提出了飞行通道的研究思路,能够将多维优化问题简化成一维搜索问题[14-18]。其中Harpold与Graves对Space Shuttle飞行器提出了阻力-速度飞行通道[1],飞行通道上限由3种传统路径约束计算得出,下限由准平衡条件计算得出。Roenneke和Markl针对飞行器能量这一变量,提出了阻力-能量通道[14]。而后,这种制造飞行通道所使用的剖面方法被展开研究,出现了速度-高度剖面、速度-航迹角剖面等剖面方法,用以形成不同性能的飞行通道[15-18]。现阶段的高超声速滑翔飞行器设计再入过程制导律时,多是在标准轨迹的基础上,通过预测反馈的结果,在飞行通道内搜索并调整控制指令,跟踪最优轨迹的动力学剖面。但是,高超声速滑翔飞行器在通道中飞行时,机动性会受限,在面对诸如禁飞区和路航点等多变空间约束环境时,有可能出现任务失败的情况。
为了减少对标准轨迹的依赖,部分学者探索了离线弹道库的方法和在线优化轨迹方法以解决飞行中复杂多变的环境问题与标准轨迹的较大偏移问题[19-21]。其中,离线弹道库的方法虽然能够大幅度减少飞行时的计算量,但是飞行器在空域内遇到的情况复杂多变,离线弹道库的方法本身存在一定的漏洞;而以伪谱法和凸优化方法为代表的最优轨迹求解方法,虽然能够求解出较为精确的优化轨迹,但是随着轨迹精度的提高以及约束复杂性的增加,求解优化轨迹的计算量将变大,而高超声速滑翔飞行器具有飞行速度大、状态变化快等特点,离线的轨迹优化方法很难实现在线的高精度轨迹优化,尤其是优化出的横向剖面控制指令连续多变,不利于高超声速滑翔飞行器这种强非线性系统的控制[22-23]。
考虑路航点约束的轨迹优化研究通常应用于无人机等低速飞行器,但是考虑到实际的位置匹配和导航需求,路航点约束也被应用到了高超声速滑翔飞行器的任务规划中[24]。而随着各国反导系统以及航空识别区的建立,禁飞区(No-Fly Zones,NFZ)约束也成为研究中不容忽视的考虑因素。目前大多数针对禁飞区约束的研究多是在离线状态下用已知的禁飞区信息求解轨迹优化的最优解。当遇到多变的禁飞区时,也有研究人员基于邻域控制的方法略微改变控制变量进行规避[25]。这类研究虽能解决部分禁飞区问题,但是针对的都是禁飞区信息已知的情况,并且要在离线状态下或者在机动制导交接点前计算轨迹,当禁飞区较小且移动速度较快或者禁飞区分布较为复杂时,这类方法的计算时间会变长且计算精度低,可靠性变差[26-29]。
近年来,部分学者应用生物学中的触角方法对高超声速滑翔飞行器的探测反馈再入制导进行了探索与改进[3-4,30]。基于触角的探测反馈方法首先应用在机器人的路径规划中,通过浓密的触角覆盖周围区域并探测周围地形[31-32]。高超声速滑翔飞行器制导策略若采取浓密的触角探测反馈,计算时间过长,无法应用于机动制导中的精细计算。梁子璇等在触角末端威胁评估方法的基础上探索了基于双触角探测的倾侧角逆转制导策略[3-4,30]:在禁飞区信息未知的情况下,仅仅判断触角末端的禁飞区情况,结合航向角约束,通过实时获得触角的剩余地面距离和时间,计算2个方向触角的威胁程度,选择较为安全的方向进行机动制导,并采用不同的禁飞区模型进行了方法的实用性和鲁棒性检验。在这一基础上,文献[3]与文献[4]增加前向飞行的触角探测,并将航向角约束的计算方法进行改进,同时使用倾侧角转换延时滤波器,讨论了多禁飞区约束情况,减少了倾侧角的转换次数,增加了飞行器无横向机动飞行时间在总飞行时间的比例。文献[4]中,增加了基于相邻时刻触角信息的实时识别禁飞区动态的预警区域模型,针对跟踪型禁飞区情况进行了仿真实验。但是,这类触角方法在飞行器再入飞行的初始阶段时用于探测的触角长度比后期触角长度大很多,在计算耗时上远大于后期触角探测过程,影响飞行器再入初期阶段的机动性能。
综上所述,当前的关于高超声速滑翔飞行器的机动制导研究虽然相对全面,但是在禁飞区信息未知情况下进行机动制导的触角方法仍有不足。为此,本文在速度-航向角约束的基础上,改进成为速度-剩余地面距离-航向角约束,并且采取双模式多触角探测反馈的方法进行机动制导策略的设计。一方面通过多触角粗略预测的结果快速获得临时目标点;另一方面,在临时目标点的基础上基于三触角的精细预测进行机动制导,并在多禁飞区模型和禁飞区通道模型情况下进行了仿真实验,仿真结果表明,该方法对于高超声速滑翔飞行器的再入机动制导过程有指导意义。
1 高超声速滑翔飞行器再入过程建模
1.1 高超声速滑翔再入飞行动力学模型
针对高超声速滑翔飞行器的再入过程,忽略地球自转角速度的影响,在地心赤道旋转坐标系内,建立以下动力学模型[33-35]:
(1)

(2)

(3)
(4)
(5)

(6)
式中:r为飞行器的地心距;V为飞行器的地球相对速度;ψ与γ分别为飞行器的航向角与航迹角;飞行器所处的经度θ和纬度φ是判断飞行器路径约束的主要因素;m和g为飞行器的质量和当前地心距的重力加速度;飞行器的倾侧角σ与攻角α分别控制飞行器制导策略中的横向、纵向制导剖面;D=ρV2SrefCD/2与L=ρV2SrefCL/2为飞行器在飞行过程中的气动阻力与升力,其中ρ为飞行器当前高度的空气密度,Sref为飞行器的参考横截面积,CL与CD分别为与飞行器攻角有关的空气动力学参数。
不同的高超声速飞行器可根据飞行试验和参数辨识来获得不同的空气动力学参数,本文选用Common Aero Vehicle-HPMARV(CAV-H)高超声速滑翔飞行器作为研究对象,该飞行器的空气动力学参数来源于文献[33]与文献[35]。
1.2 常规约束与禁飞区约束
高超声速滑翔飞行器在临近空间的飞行过程中,要面临多种约束的限制。本文中CAV-H沿标准轨迹规避禁飞区进行机动制导,主要考虑飞行器飞行任务中的始末两端的端点约束以及多种路径约束。始末两端的端点约束是根据任务条件给出的,其中初始端点约束是任务的初始状态,也是生成的标准轨迹和机动制导的开始状态。令X=[r,θ,φ,V,γ,ψ]T为飞行器状态矩阵,εX为较小的常值矩阵,维数与X相同。终端约束模型为
(7)
式中:上标i表示矩阵第i个元素;下标f代表终端状态;tf表示终端时间。εX越小,飞行器标准轨迹与机动制导的终端状态越接近任务的终止状态,机动制导的结果越精确。
常规路径约束,包括热流率约束、过载约束和动压约束,其数学模型分别为[36]
Q=KQρ0.5V3.15≤Qmax
(8)
(9)
(10)
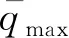

图1 多圆柱形禁飞区模型Fig.1 Multi-cylinder no-fly zone model
本文中的禁飞区均考虑为垂直于地球表面的柱形禁飞区,其横截面可以是不同的形状。假设禁飞区有N个,如图1所示,飞行器距离第i个禁飞区边界的最小距离为di(i=1,2,…,N),当飞行器在禁飞区外,di为正,如果存在di不为正,则飞行器没有成功规避禁飞区。因此,高超声速滑翔飞行器应根据飞行任务及时转弯并规避禁飞区。
1.3 航向角约束
在飞行器机动制导过程中,采用航向角约束可以避免飞行器机动后无法到达任务目标。飞行器要根据其在机动过程中的速度和剩余地面距离来确定这种约束,使得飞行器能够有足够的距离通过对倾侧角和攻角的控制,把飞行器制导到终点或者临时终端位置。在基于触角探测反馈的倾侧角横向瞬变制导策略中,任务目标仅仅是最终位置,只需要速度这一种变量作为航向角约束的参考值。本文考虑加入与飞行器距离较近临时路航点,减少探测反馈时间,因此将距离终点或者临时路航点的剩余地面距离也作为航向角约束的参考变量。
首先,将航向角约束定义为在经纬平面中飞行器当前位置指向目标点的向量与飞行器初始位置指向目标点向量的夹角,如图2所示。然后,求出飞行器在满足初始任务中速度、高度条件下的最大转弯轨迹,在该轨迹上求出各个轨迹点Pj(j=1,2,…,m)的速度、方向、位置与剩余地面距离。令轨迹点到终点连线与速度方向的夹角Ψi(i=1,2,…,m)为当前航向角误差,顺时针为正方向,即
Ψi=|ψi+arctan((θi-θf)/(φi-φf))-π/2|
(11)
式中:θi、φi和ψi为当前轨迹点Pi位置的经纬度坐标和航向角;θf、φf为终点的经纬度坐标。最后,航向角误差与速度、剩余地面距离的关系如图3中所示。其中,航向角误差为飞行器实时位置的航向角与初始航向角之间的偏差。
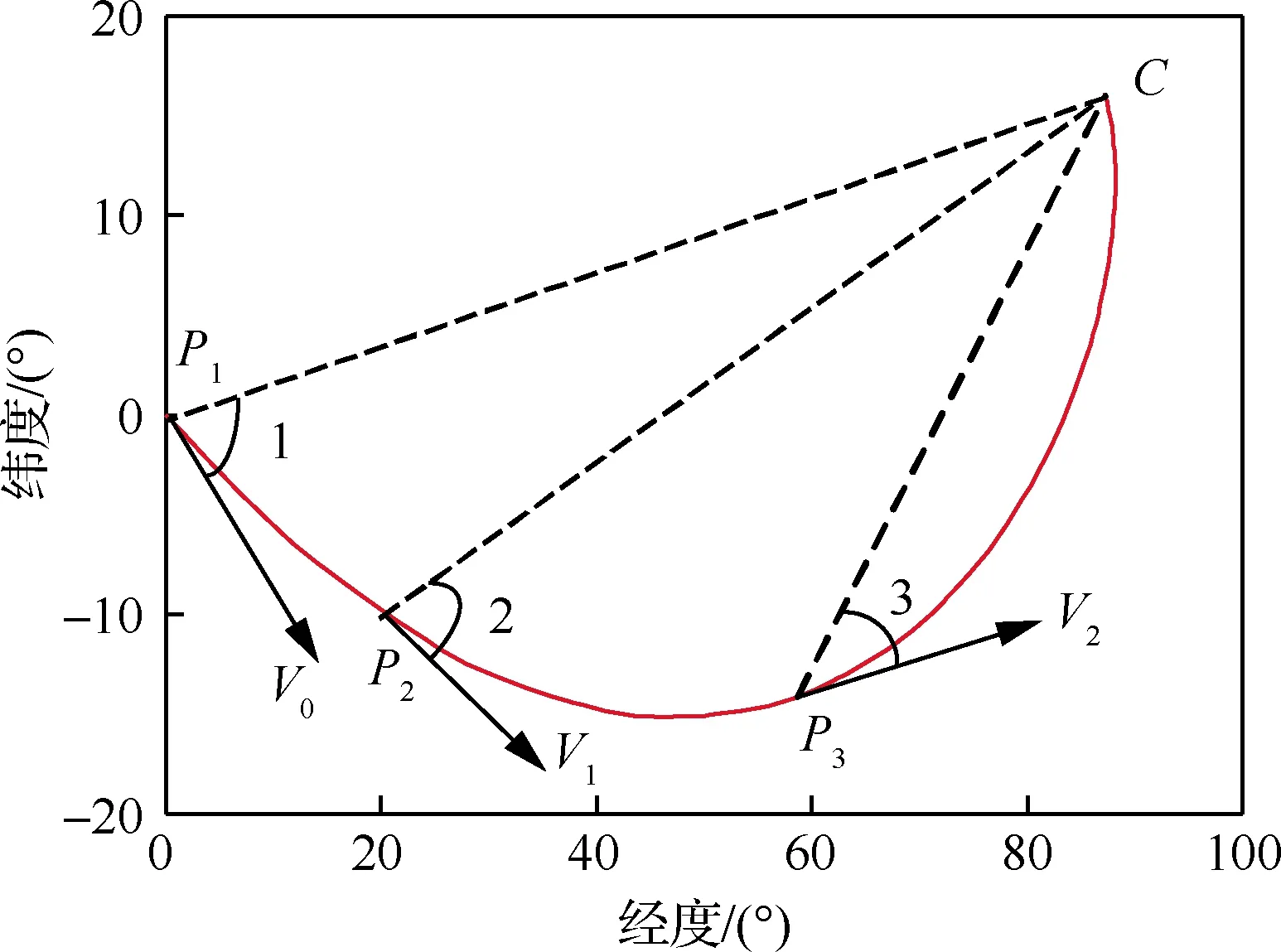
图2 飞行器最大转弯轨迹Fig.2 Maximum turning trajectory of vehicle
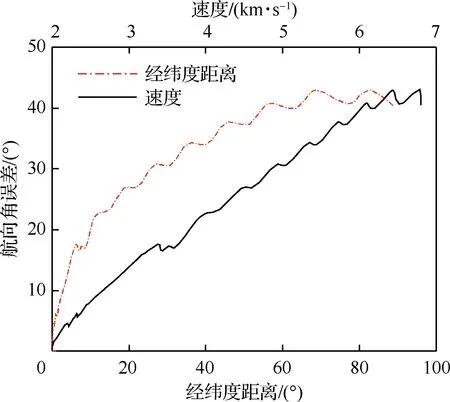
图3 航向角误差约束Fig.3 Heading angle error constraint
2 基于触角的探测反馈模型
本文在研究禁飞区条件下飞行器机动制导前,通过高斯伪谱法在没有禁飞区的条件下获得最优路径[37-38],之后根据最优路径的信息在满足其他路径约束的情况下规避禁飞区,机动制导到终点区域。首先建立基于多触角的分段定点探测反馈机制,之后根据多触角的反馈,实现临时终端点的确定,最后在分段制导的过程中,采取基于三触角的探测反馈机制进行机动制导。在基于触角的探测反馈机制中,按方向划分制导策略,分为纵向制导策略和横向机动制导策略,纵向制导策略通过线性二次调节器(Linear Quadratic Regulator, LQR)方法实现,横向机动制导策略由基于多触角探测的倾侧角瞬变制导方法实现。
2.1 基于LQR方法的纵向跟踪制导策略
由于标准轨迹是由高斯伪谱法等优化方法得到的时间上不等间距的状态点,在实施LQR方法跟踪标准轨迹时,在时间轴上,第i时刻要跟踪的第(i+1)时刻的状态,必须要提前计算出第(i+1)时刻的状态。为此,就要将标准轨迹的状态信息进行线性差值,获得一系列等间距的状态点。令飞行器在标准轨迹中距离出发点的经纬度距离为线性化过程中的自变量,由于标准估计没有进行机动,航向角不变,因而线性化的状态信息只有[>r,V,ψ]T3个变量,最后根据经纬度距离最近的两个标准轨迹点对该经纬度距离的状态进行线性化估计,即
(12)

Δαi=K(s)(Xi-Yi)
(13)
式中:K(s)由LQR算法求得;Δαi为实时求得的第i时刻的攻角变化量。
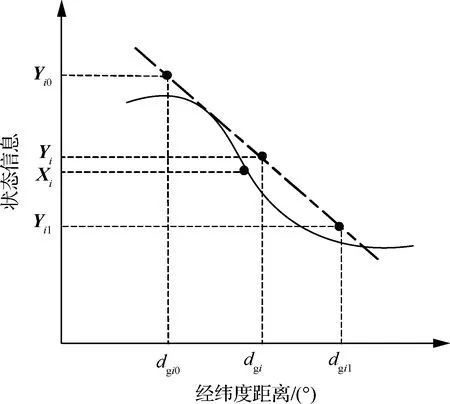
图4 第i时刻状态变量线性化Fig.4 Linearization of state variable at i th moment
2.2 触角的产生与停止
在高超声速滑翔飞行器沿标准轨迹进行机动制导的过程中,前方路径中的禁飞区约束情况是未知的,同时由于机动制导带来的常规路径约束是否超出限值也是未知的,因此需要产生多个触角对前方路径进行探测。而后,飞行器在触角探测反馈后会根据触角终点的信息选择其中一个触角进行跟踪飞行。
所有的探测触角均采用同一方法产生,每一个触角拥有不变的倾侧角,每一个触角的出发点是一致的,假设飞行器处于第i时刻,以当前控制指令仿真积分一个时间步长ΔTLat后,令积分后的第i+1时刻的状态为预测起点,当这一预测周期结束、获得相应的信息并计算出控制指令后,飞行器也刚刚飞至第i+1时刻的状态,由于积分时间步长固定且较小,预测起点与实际状态误差较小,并且在飞行过程中,这一极小的误差可以由2.1节中的跟踪制导模型弥补。每个触角的终止条件如下[4,30]:
C1:触角的积分时间与已飞行时间之和超过任务最大飞行时间,本文最大任务时间设为3 000 s。
C2:存在触角末端在任意禁飞区边缘或者内部。
C3:存在触角上的状态信息经过计算后超出了热流率约束、动压约束和过载约束3个路径约束的最大值。
C4:触角的末端超出了根据速度或剩余地面距离获得的航向角限制。
C5:触角末端到达终端区域。
其中,前4个条件属于禁忌条件,飞行器的机动制导过程都应避免沿着这4种条件的触角飞行,而C5属于容许条件,飞行器在规避禁飞区并且满足其他路径约束条件时要尽量选择这种触角。
3 双模式的触角探测反馈制导策略
在高超声速滑翔飞行器机动制导过程中,如果只有一个距离较远的终点,飞行器若使用2个或者3个触角实时探测前方未知情况,初始阶段计算耗时较大。为了降低初始阶段的触角探测耗时,采用2种触角探测模式:① 多触角大积分步长的粗略探测,进行总任务的分段定点,得到临时路航点;② 三触角小积分步长精细探测,用于分段后指向临时路航点的机动制导,两种方法在飞行器沿标准轨迹制导的过程中同时进行。
3.1 触角探测中的多触角粗略探测定点策略
图5为多触角探测临时路航点的示意图。飞行器在O点发出多条红色的大步长触角进行探测,判断触角状态后,最终选择绿色的触角末端作为临时路航点。
图6为多触角探测临时路航点获取的流程图。首先要使用大步长的多触角进行探测,令飞行器从出发点开始以时间为预测周期,产生p条大步长触角,第k条触角的倾侧角为

图5 多触角临时定点策略Fig.5 Multi-tentacle temporary fixed point strategy

图6 多触角临时路航点获取Fig.6 Multi-tentacle temporary waypoints acquisition
σk=-σmax+2σmax(k-1)/(p-1)
(14)
式中:σmax为倾侧角最大值。当预测的触角停止后,得到所有触角的停止条件集合和停止端点的状态信息。参考优先级计算方法,计算停止优先级矩阵Ka和末端状态优先级矩阵Kb[4]。
令5种停止条件的停止优先级矩阵Ka为[a1,a2,a3,a4,a5],第k(k=1,2,…,m)条触角的停止优先级为Kak。然后,根据各个触角的末端经纬度计算末端状态优先级Kb,假设当前所有触角的出发点经纬度为[φ0,ψ0],第k条触角的末端经纬度为[φk,ψk],终点的经纬度为[φf,ψf],计算距离dgk:
(15)
之后,把所有触角的dgk由小到大排列,按照大小顺序分别赋予末端状态优先级,形成的第k个触角的末端状态优先级Kbk分别为{b1,b2,…,bm}K=1,2,…,m将每一条触角的两种优先级做乘法,即总优先级为Kk=-KakKbk,通过比较所有的总优先级,得到应该选择的机动制导倾侧角,即
σ=σcKc=max(Kk)
(16)
Kmax=max{K1,K2,…,Km}
(17)
(18)
式中:σc为通过比较总优先级获得的倾侧角,c是当前预测周期内被选择的那条触角序号;Dc为被选择的触角的始末距离。
为保证总优先级合理,设置2种优先级矩阵Ka和Kb的关系式为
a2=a3>a4>a1>a5>0
(19)
0 (20) (21) 其中:式(19)与式(20)的下标分别代表禁忌条件编号和末端状态优先级的从小到大赋值编号,并不代表触角编号。式(19)强调的是Ka中禁忌条件与允许条件之间的关系;式(20)强调的是同一种停止条件下根据末端状态的优先级关系,且所有元素小于1是保证Ka中较小的触角不会因为Kb较大而总优先级小于Ka中较大的触角;式(21)是为了优先考虑停止条件优先级,避免Ka中较为禁忌的触角由于Kb较小而总优先级大于Ka中较小的触角,ka代表产生上述可能的临界值。本文选择的Ka和Kb矩阵分别为[0.1,1,1,0.4,0.05]和bi=0.75+0.01i,其中i是Kb矩阵根据末端状态优先级从小到大排列后的序号,满足式(19)~式(21)的限制条件。 最后,设定分段定点模式中的地面距离固定为Dg。令Dg与Dc比较,如果Dg大于Dc,则选择Dc所代表的位置为临时路航点,即分段点;如果Dg小于等于Dc,选择第c条触角距离触角出发点距离Dg的点为临时路航点。由于触角生成终止的规则中已经考虑到了多种典型的再入约束,如果生成的触角不满足再入约束,是不会引入到触角探测候选的,因此得到的临时航路点也能满足再入约束。临时路航点选择后,将作为分段制导模式下的三触角横向探测反馈机动制导的临时终点,即更换了2.2节中的触角终止条件C5的终点,同时也改变了条件C4中参考剩余地面距离的航向角约束。 将3.1节中产生的临时终点作为三触角探测反馈的“终点”进行机动制导,当飞行器的经纬度位置与临时终点的距离小于与任务终点的距离,则将任务终点作为机动制导终点直到最后,可以达到节省制导计算时间的目的。 首先,确定三触角模式的预测周期T2,该模式下,预测时的积分周期远小于多触角探测定点模式,即三触角模式下每一个预测周期只取3个触角,并令p=3,他们的倾侧角分别为[-σmax,0,σmax]。Ka和Kb矩阵分别为[0.1,1,1,0.4,0.05]和[0.75,0.76,0.77],满足3.1节的优先级规则。 然后,在初步确定了第i个预测周期的倾侧角σi后,为了避免经过此过程产生的倾侧角在一段时间内产生高频率的震荡或者不必要的左右摇摆,引入延时滤波器如下[4]: σr= (22) 式中:T为延时滤波器的时间常数;σr为第i时刻最终输出的倾侧角值,滤波器从第(T+1)时刻开始工作,因此T选取的值过大会导致飞行器无法及时机动制导并规避约束,式(22)中的kσ为T的三分之一。 本文研究的飞行器是CAV-H,其质量为907.2 kg,气动力横截面积为0.484 m2,最大热流率为4 MW/m2,最大动压为60 kPa,最大过载为2.5g,其飞行任务数据如表1所示[4,30,40]: 为了验证本文算法的适用性,首先在没有禁飞区约束的情况下根据始末状态设计标准轨迹,设计标准轨迹的过程中,控制飞行器横向机动的倾侧角为0,如图7所示。同时,令飞行器以标准轨迹为基准在4种具有代表性的禁飞区情况下完成机动制导仿真实验。 1) 由左右2个半圆分布的圆柱形禁飞区形成的包围分布禁飞区。 表1 CAV-H飞行始末状态条件Table 1 Initial and terminal conditions of CAV-H 图7 标准轨迹高度、速度时间变化Fig.7 Altitude and velocity of standard trajectory 2) 均匀分布在始末两端中间的三列圆柱形禁飞区。 3) 由两个矩形禁飞区构成的飞行走廊。 4) 正弦曲线形状的禁飞区构成的通道。 仿真实验中,在没有禁飞区的情况下获得标准轨迹后,飞行器是在提前不知道禁飞区具体形状的情况下,仅通过触角的探测反馈得出某一点有禁飞区并且不能通过。 根据表1中的飞行数据以及4种禁飞区约束条件,使用基于触角探测的双模机动制导策略,获得了地面制导轨迹路线与控制指令,如图8和图9 所示。其中图8为4种禁飞区情况下的经纬度轨迹路线图,图8(a)与图8(b)中的黑色圆圈代表的是半径为0.5°(3 198 km)和0.6°(3 826.8 km)的圆柱形禁飞区,红色圆圈表示的是在每一个分段定点周期内,选择的临时终端点。仿真实验中,多触角探测定点模式的积分周期设置为10 s,而三触角机动制导模式的积分周期设置为1 s,每100 s执行一次多触角探测定点模式,每1 s执行三触角机动制导模式,各个任务中的定点参考距离设置为18°(115 128 km)。 由图8看出,针对每一个禁飞区任务,算法一方面由多触角探测定点模式产生临时终端点,另一方面通过蓝色的触角在临时终端点的基础上进行机动制导。在每一个任务的初始阶段,临时终端根据分段定点模式7条触角的末端位置进行不断地更新,产生了较为连贯的临时终端点;当飞行器距离真实终点的距离即将达到分段距离Dg时,临时终点基本都聚集在终点位置[100,0]。 图9为4种禁飞区任务中的控制指令随时间的变化图,其中蓝色的虚线代表的是由纵向跟踪制导策略产生的攻角指令,攻角指令变化次数较多,实现对标准轨迹的跟踪,红色实线代表的是经过延时滤波器滤波后的倾侧角。可以明显看到,飞行器在规避各种复杂的禁飞区任务时,采取的倾侧角瞬变次数较少,能够有效规避禁飞区和航向角限制。并且,4种任务中,当飞行器需要由一个带有倾侧角的机动方向转到反方向机动时,即飞行器在经历倾侧角正负逆转时,延时滤波器会令倾侧角在这期间经历一段归零的过程,防止倾侧角的变化过大、切换频率过快造成飞行器失稳。 图10为3种路径约束在机动过程中随时间的变化图,其中每张路径约束变化图从上到下分别为动压、过载、热流率约束变化。在触角停止条件中加入的三大路径约束停止条件,有效地避免了飞行器在加入倾侧角机动后产生路径约束上可能超出的情况。在图10中,红色虚线代表3种约束的上限值,蓝色实线代表实际的约束变化。由图10可见飞行器在4种禁飞区任务下的机动制导过程,完全满足热流率、动压和过载约束。 图9 4种禁飞区情况下的控制指令Fig.9 Control commands in four NFZs 图10 4种禁飞区情况下的路径约束Fig.10 Path constraints in four NFZs 为了验证算法在初始状态离散的情况下的鲁棒性,将以上4种任务中的初始状态和飞行器本身参数采用蒙特卡洛方法进行随机离散。其中,对于状态矩阵中的变量采取表1中的3σ原则进行离散,飞行器的质量、空气动力学系数分别按照10%和5%的比例进行离散。随后将离散后的初始条件代入模型进行验证实验,每一个任务分别进行1 000次实验,各禁飞区任务的轨迹簇如图11 所示,每一个任务中的高超声速滑翔飞行器机动制导过程均获得成功。 图11(a)中,有2次实验的机动制导轨迹略微偏离大部分轨迹,是因为在多触角定点策略中采用的是7条粗略预测触角,如果在定点模式中增加探测触角的数量,轨迹簇会更为集中。 如图12所示,在蒙特卡洛仿真实验中,将4个任务的1 000次蒙特卡洛实验中热流率、动压和过载3种约束的最大值数值和出现的时间点分别进行记录。图12中,每一个任务的热流率、动压和过载约束都符合飞行器的设计要求,并且在动压约束方面,各个任务的动压最大值分布较为集中,体现了模型的鲁棒性。图13中展示的是蒙特卡洛实验中,4种任务共4 000次仿真实验的飞行器速度跟踪情况,可见模型的LQR算法使得飞行器在机动制导过程中的速度参考经度这一变量基本上跟踪上了标准轨迹的飞行器速度。因此,本文提出的多触角探测下高超声速滑翔飞行器再入机动制导方法具有很好的鲁棒性和稳定性。 图11 4种禁飞区情况下轨迹簇Fig.11 Trajectories in four NFZs 为了检验算法用于高超声速滑翔飞行器机动制导时在计算时间上的有效性和可靠性,在飞行器进行4种禁飞区任务双模式的机动制导过程中,记录每一次多触角探测定点的计算时间以及三触角探测机动制导的计算时间,研究中采用的电脑和软件分别是CPU:3.2 GHz的台式机和MATLAB 2018a。获得整个任务的计算时间集合后,分别作两种计算时间随飞行时间的变化图。 图13 鲁棒性实验速度跟踪情况Fig.13 Robustness experiment speed tracking 如图14所示,实线的4条曲线是多触角分段定点模式的计算时间,其中每一次飞行任务中的多触角探测定点次数由定点时间间隔决定。图14中,多触角探测定点策略的计算时间符合由大到小的趋势,因为在任务初始阶段,飞行器飞行任务的剩余地面距离较大,触角的探测距离较长。 任务一中在400 s左右和1 300 s左右各出现一次大的计算时间的反弹,是由任务一中禁飞区的特征决定的,飞行器在这两个时间段应恰好经过由圆柱形禁飞区构成的两道包围圈,这两个阶段是触角探测长度的临界变化阶段。在任务二中,由于飞行器经过均匀分布的禁飞区时,左右的禁飞区时有时无,多触角探测的距离也是相应的时长时短,直接造成了任务二中多触角探测定点时间的常态波动。相反,任务三和任务四的禁飞区形状较为整齐,所得到的多触角探测定点计算时间随飞行时间的增大,下降趋势明显。另外,图14 中的4条点划线代表4种任务中三触角机动制导模式的计算时间,可见机动制导模式的耗时远小于分段定点模式的耗时。 图14 双模式计算时间变化Fig.14 Dual mode computing time variation 图15和图16为蒙特卡洛实验中4 000次实验2种触角探测反馈模式的计算时间特性,在每一次蒙特卡洛实验中,分别记录该实验中2种模式的计算时间最大值、最小值以及出现这些值的飞行时刻。再计算每一次实验中2个模式的计算时间平均值,找出与平均值相类似的计算时间时刻点并进行记录。由图15与图16可见,2种模式的计算时间均很短,基于多触角探测反馈的机动制导策略能够在时间上满足高超声速滑翔飞行器机动制导的要求。 图15 分段定点模式耗时特点Fig.15 Time-consuming characteristics of segmented fixed point mode 图16 机动制导模式计算时间变化Fig.16 Time-consuming characteristics of maneuvering guidance mode 在分段定点模式中,临时路航点的选取不仅由禁飞区信息决定,也受到定点参考距离和定点时间的影响。为验证不同定点参考距离和不同定点时间对于分段定点模式路航点选取和对本文模型稳定性的影响,在任务一的禁飞区条件下,采取控制变量方法分别测试2种因素的作用。 一是采取6种不同的定点参考距离Δdr,分别取5°,15°,20°,30°,50°,70°,定点时间间隔固定为40 s,从图17中可以发现,Δdr越小,得到临时路航点越密集。虽然6种情况下的机动制导实验都能顺利完成,但当定点参考距过小或者过大时,轨迹不易收敛至中心轴线。图18中展示了不同定点参考距离对于计算时间的影响,其中,计算时间最大值和最小值未受太大影响,而机动制导的平均预测时间随着定点参考距离变大而变大。需要说明的是,在图18和图19中,为了使得时间大小的差别在作图时表现的更为明显,纵坐标的刻度采用了Matlab中log为底的对数形式进行尺度刻画,但是每个小刻度对应的数值对于时间间隔仍是均匀的。 图17 不同参考间隔的飞行轨迹Fig.17 Flight trajectories with different reference intervals 二是采取6种不同的定点预测时间间隔Δtr,分别是10 s,30 s,50 s,100 s,200 s,500 s,定点参考距离是18°,从图20中可见,Δtr越小,得到临时路航点越密集,当定点时间为500 s时,由于第一次定的临时终端点在中轴线上,在下1次预测定点前,飞行器发出的触角已经全部打在位于飞行器正前方的小禁飞区上。对比前面5种定点预测时间间隔的机动制导结果,飞行器的第1次临时终端点虽然都相同,但是前5次实验都因为分段定点的预测时间间隔较短,使得飞行器在未飞至第1次临时终端点的时候就已经重新定点,而这5次实验中更新后的临时路航点均是在第一包围圈外,使得飞行器能够机动制导出去。由于预测时间间隔变化并不影响每次临时路航点与飞行器之间的距离,因此不同定点预测时间间隔对于图19中的计算时间影响较小。 图18 不同参考间隔的耗时特性Fig.18 Time-consuming characteristics of different reference interval 图19 不同定点预测时间的耗时特性Fig.19 Time-consuming characteristics of different fixed-point forecast time 本文通过对基于触角的预测校正制导方法的改进,采取2种多触角探测模式相结合的方法,提出了基于多触角的高超声速滑翔器再入机动制导策略。 1) 该制导策略极大地降低了预测反馈的计算时间,仿真中双模式的计算时间特性体现了该方法满足机动制导的要求。 2) 通过控制变量方法验证不同定点参考距离和定点预测时间间隔对机动制导效果影响,从而得知,定点预测时间间隔对机动制导的影响较大。 3) 通过4种禁飞区任务的蒙特卡洛仿真实验验证了该方法的鲁棒性。 综上,本文提出的基于多触角探测的再入机动制导策略能够较好地应用在高超声速滑翔飞行器的研究中。3.2 分段制导模式下的三触角探测反馈制导策略
4 仿真算例与分析

4.1 不同禁飞区条件的飞行仿真

4.2 蒙特卡洛仿真与分析

4.3 算法消耗时间分析


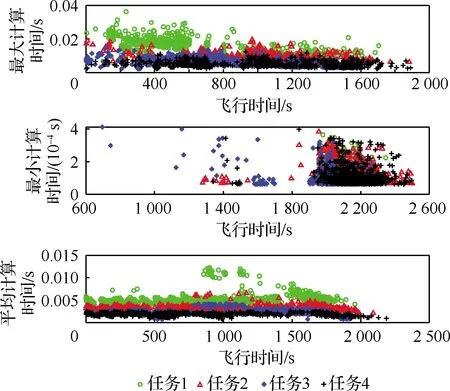
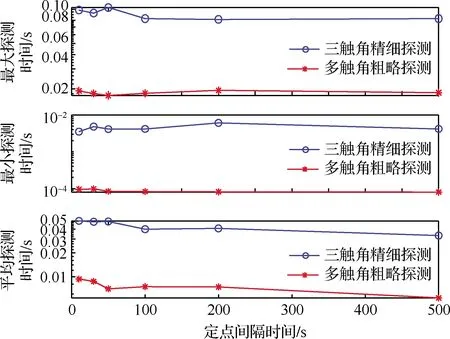
4.4 不同定点参考距离和定点时间影响分析


5 结 论

