某退役油罐氮气惰化数值模拟

刘瑞 王冬 张培理 梁建军 郭子航 党金鹏 赵亚东

摘      要：目前我国很多油库油罐是20世纪60—70年代修建，已达到退役年限，随之而来这些退役油罐面临封存停用问题。基于湍流k-ε标准模型，对某退役覆土1 000 m3立式拱顶油罐进行氮气惰化数值模拟研究。重点研究了油罐氮气惰化过程中随氮气进口流量变化时，氧气体积分数分布和油罐拱顶压力变化规律。研究结果表明：相同氮气进口流量时，油罐内氧气体积分数随时间不断降低，且开始阶段降低速度较快，之后较为平缓;氮气进口流量越大惰化时间越短，同时为保护油罐拱顶对流量有相应限制;工程实践中油罐惰化对氧气体积分数提出了安全临界值。为大量退役油罐安全处置提供参考方案。

关  键  词：退役油罐;氮气;进口速度;惰化;油罐拱顶;压力;数值模拟

中图分类号：TE 88        文献标识码： A       文章编号： 1671-0460（2020）09-2050-05

Abstract： Many of the oil tanks in our country have been built in1960s-1970s，now they have been decommissioned， and these decommissioned tanks are facing the mothballing problem. Based on the turbulent k-ε standard model， the numerical simulation of nitrogen inerting method was carried out for a 1 000 m3 decommissioned vertical arch tank. The distribution of oxygen volume fraction and the change law of pressure of oil tank dome were studied when nitrogen inlet flow changed in the process of nitrogen inerting in oil tank. The results showed that， with the same nitrogen inlet flow rate， the volume fraction of oxygen in the tank decreased continuously with time， and the decrease rate was faster in the initial stage， and then was relatively stable; The larger the nitrogen inlet flow rate， the shorter the inerting time. At the same time， the flow was limited to protect the oil tank dome; In engineering practice， the safety critical value of oxygen volume fraction in nitrogen inerting was proposed.It provides a reference scheme for the safe disposal of large number of decommissioned oil tanks.

Key words： Decommissioned oil tank; Nitrogen; Inlet speed; Inerting; Tank dome; Pressure; Numerical simulation

目前我国很多油库油罐是20世纪60-70年代修建，这些油罐已达到退役年限。这些退役油库隐藏着大量的油气危险源，面临管理人员少，周围情况复杂，部分油库退役油罐位于闹市区，如果不能妥善处置随时可能引发燃烧爆炸，造成大量的人员伤亡、财产损失以及环境污染等危害。因此对退役油罐的安全处置研究，具有重大意义[1]。

目前直接研究退役油罐安全处置文献资料较少，但是对一些油气危险源安全处置方法可以借鉴。国内外学者采用模拟实验和数值模拟研究油气危险源处置较多，大量研究表明惰性气体对爆炸具有较好抑制作用[2-6]。有文献[2]指出，随着初始混合气体中惰性气体氮气或二氧化碳含量的升高，瓦斯爆炸超压均明显降低;氮气和二氧化碳对较高浓度瓦斯气的抑爆效果更为显著。李恩田[3]等对浮顶油罐的油气空间进行惰化，根据氮气对油罐气体空间的惰化原理，针对大型双重密封型浮顶油罐的油气空间进行氮气惰化研究。张培理[4]等以燃惰气为介质，实验研究进气口位置和进气体积流量对燃惰气惰化置换油罐油气的影响。

本文主要通过数值模拟研究某退役覆土立式油罐氮气惰化过程[7-8]，建立了适合惰化的湍流k-ε标准模型[9-10]，采用PISO [11]算法对离散后的控制方程进行求解。本文重点研究了油罐氮气惰化过程中随氮气进口流量变化，氧气体积分数分布和油罐顶部压力变化规律。

1  构建退役油罐惰化模型

1.1  几何模型与网格划分

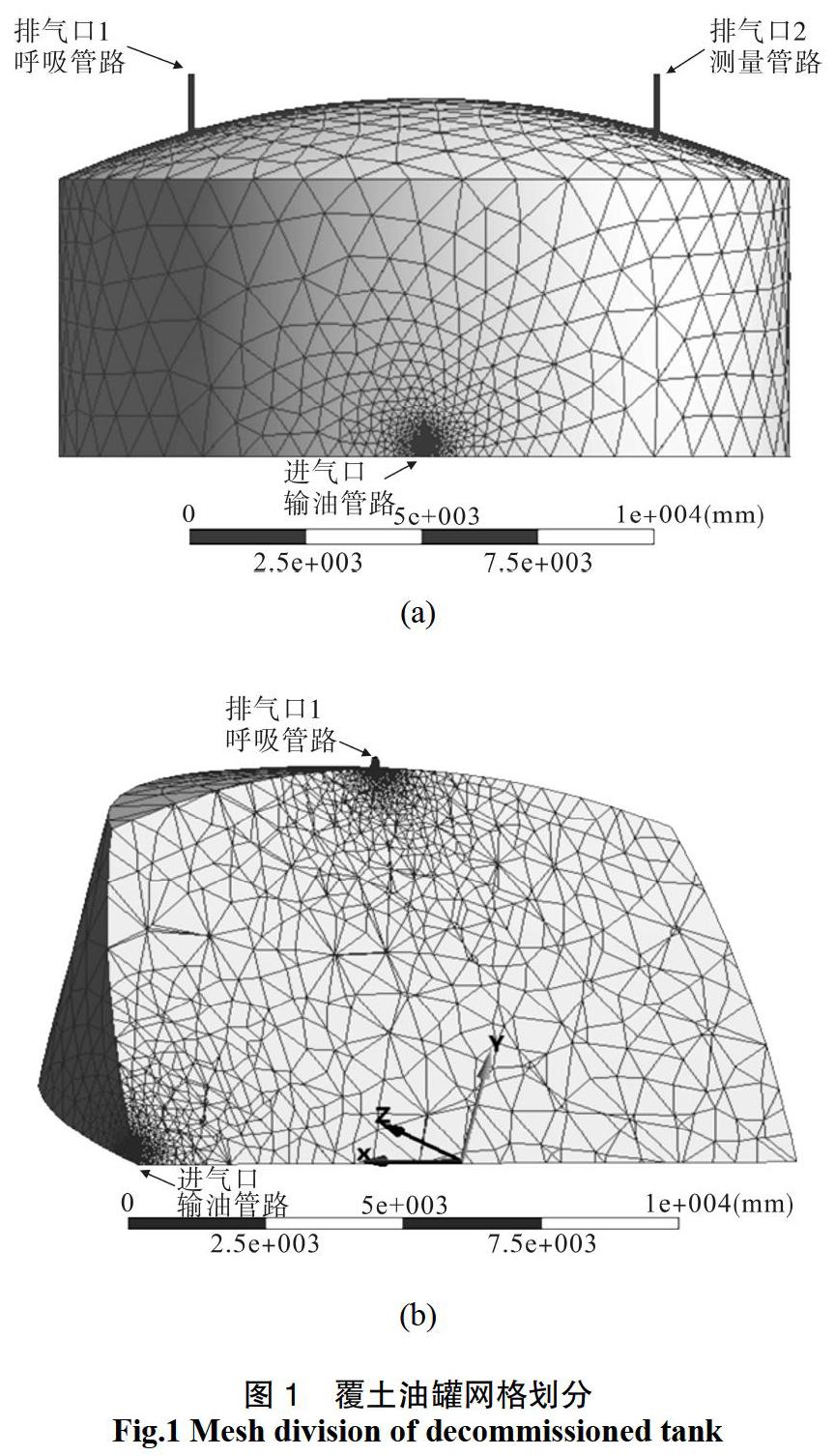
以华北某油库为例，该油库有4座1 000 m3退役覆土油罐，且油罐罐底超過50年未更换。通过调查发现罐内油气味较大，且超过油气浓度爆炸下限，危险性较大。现利用覆土油罐原形尺寸构建模型，直径为15 725 mm，壁高5 900 mm，顶高7 600 mm，在固定顶对称布置测量管路、呼吸管路各1个，直径均为150 mm，测量管路和呼吸管路中心距油罐中心5 000 mm，输油管道中心轴线距罐底300 mm处有管道，直径150 mm。划分网格（图1），生成网格数75 585个，节点数15 317个。图中展示了呼吸管路、测量管路、输油管路位置以及坐标位置。排气口1和2中心坐标为（0 m，8 m，5 m），（0 m，8 m，5 m）及罐顶点（0 m，7.6 m，0 m）。

1.2  基本假设和控制方程

覆土罐罐室内油气惰化过程是一个典型的瞬态传质扩散过程，通过氮气置换出油气混合物中氧气，使氧气浓度置换到爆炸下限即可达到不燃不爆本质安全型油罐[12]。采用计算流体力学模型对瞬态组分输运过程进行模拟。本论文做了以下假设和简化：

1）覆土罐内为油气混合物，无液态汽油，不予考虑汽油相变[13]过程，初始气体分布均匀，无流动，气压为标准大气压，遵循理想气体状态方程;

2）气体的整个运动过程维持热平衡，忽略其温度差异和热量传递;

3）油罐内仅考虑氧气、氮气与油气（用C8H18代替），不考虑其他组分的混合气体，该混合气体视为理想气体，遵循理想气体状态方程，在流动过程中不发生化学变化。

基于以上的简化和假设，认为覆土油罐内油气惰化过程是无化学反应的瞬态单相多组分扩散问题。因此，需要根据连续性方程、NS动量方程、组分方程建立基本控制方程组。

1.3  湍流模型

该油罐惰化过程适用于的湍流模型k-ε标准模型[14]，该模型是求解紊流动能方程k和紊流耗散方程ε，模型系数通过试验拟合得到，适合完全湍流，可以处理浮力和压缩性等物理现象。对于退役油罐氮气惰化情况完全湍流，因此宜采用 k-ε标准模型。

1.4  初始条件与边界条件

考虑工程实际，利用油罐进出油管作为惰化进气口，油罐呼吸管路及测量管路作为排出口。在相应管路上装上阀门或盲板方便在油罐惰化完成后及时对油罐快速密封，避免拆去和安装笨重的上下人孔盖。以汽油蒸气、氧气、氮气的混合物为研究对象，进行数值模拟，取惰化前混合物中油气用C8H18代替，不考虑其他组分，油气占体积分数为5%，氧气体积分数占19.95%，氮气体积分数占75.05%，由于在本数值模拟中以质量浓度进行计算，故转换为相应质量浓度为汽油蒸气占质量分数为17.22%，氧气质量分数占19.29%，氮气质量分数占63.49%。通入置换氮气为纯度为100%，设置环境为常温（293.15 K）、常压，进口速度分别为5、10、15 m·s-1，对应进口流量为318、 636、954 m3·h-1，油罐两个出口设为压力出口，因与大气相通，故相对压力设为0，排气口气体组分为空气。

1.5  求解算法

PISO 算法不需要迭代既可以具有与迭代的全隐式算法相同的精度，又可以取较大的时间步长，用于可压缩及不可压缩流动均适合。本文退役油罐氮气惰化的数值模拟是典型的瞬态扩散问题，因此采用了PISO 算法对离散后的控制方程进行求解更具优势。

2  计算结果分析

2.1  相同进气流量时氧气浓度分布规律

在常温常压下油气爆炸的临界氧气体积分数为11.4%，对应的爆炸极限临界点为1.22%[15]。由于本文退役油罐中底部仍然底油和油泥等未处理完油料，即使惰化后，在后期油气挥发仍然会出现油气浓度升高现象，因此本文不宜采用油气浓度爆炸临界点作为惰化标准，而应以氧气浓度作为标准。为了确保惰化以后退役油罐绝对安全，把氧气体积分数控制到临界值的40%，氧气体积分数为4.56%。为了紧密结合工程实际，将质量分数转化为相应体积分数，便于观察使用。

以氮气进口速度为10 m·s-1为例，进行氧气体积分数变化分析。氮气通入时间20 000 s，时间步长10 s，每10步保存一次。为了便于观察，将油罐整体向上倾斜一定角度。图2为对退役油罐在7 000 s内氮气惰化过程中氧气体积分数分布。通过500 s及 1 000 s氧气体积分数分布图，很容易发现整个油罐惰化死角出现在油罐进气口两侧中部偏下位置。在惰化过程中油罐内氧气未均匀分布，有惰化死角出现，为了说明问题，單独将6 200 s氧气体积分数分布图（图3）用单独体积分数颜色标尺，显示氧气体积分数最高处仅为5.039%，也是远远低于临界氧气体积分数11.4%。因此，在工程实践中，为便于测量氧气浓度，一般情况下仅测量在排出口处氧气体积分数低于4.56%即可。

结合图2、图3和图4分析得出：①通过曲线分析，随着氮气不断进入油罐，油罐内氧气体积分数不断降低，且刚开始降低速度较快，之后较为平缓;②当氮气进口流量为636 m3·h-1（进口速度为10 m·s-1），在6 200 s时，排气口处氧气体积分数低于4.56%，油罐内为本质安全状态。

2.2  不同进气流量时氧气体积分数对比变化规律

根据2.1可知，采用排气口氧气体积分数作为鉴定油罐惰化情况完全符合要求。通过对比分析不同氮气进口速度，数值分析得到不同进口速度排出口氧气体积分数（表1），再结合不同时刻排出口氧气体积分数变化，绘出曲线（图5）。

综上所述得出如下结论：①氮气进口流量分别为318、636、954 m3·h-1 （对应进口速度分别为5、10、15 m·s-1）时达到氧气体积分数4.56%所需时间分别12 500 s、6 200 s和4 100 s;②在16 000 s时，氮气进口流量954 m3·h-1（进口速度为15 m·s-1），此时油罐内几乎没有氧气，排出口氧气体积分数低于1%;③观察曲线（图5），氮气进口流量954 m3·h-1时，在16 000 s后曲线几乎与水平轴重合，氧气体积分数几乎不变。

2.3  进口流量对油罐拱顶安全影响

退役油罐氮气惰化过程中，整个油罐承受正压力，最薄弱部位以及最容易失稳部位是油罐拱顶[16]，本油罐拱顶承受最大正压力为2 000 Pa。由于惰化完成后还需要对退役油罐进行密封处置，因此必须确保退役油罐在惰化过程中的不受任何损坏。

下面以进口流量636 m3·h-1（进口速度10 m·s-1）为例进行分析。从油罐拱顶点（0 m，7.6 m，0 m）压力变化曲线（图6）可以看出，在15 000 s之前该点压力波动较大，在15 000 s之后该点压力相对稳定在某一很小的区域内。因此，取在15 000 s之后进口速度10 m·s-1时油罐顶部压力分布云图（图7）进行分析，发现除了两个排气口以外，拱顶压力基本在79～93 Pa波动。

结合图6和图7分析得到，油罐拱顶压力达到稳定后，从工程实践角度考虑，留有一定安全余量，取稳定后波动较大值93 Pa作为计算标准。同理得到其他进口速度时拱顶稳定压力（表2），绘出不同氮气进口速度时油罐拱顶稳定压力变化曲线（图8）。根据该油罐拱顶设计压力，再结合图8，可以得到油罐拱顶限制进口速度为46.6 m·s-1（流量为2 963 m3·h-1）。综合以上分析可得出以下结论：①在同一进口流量下，开始阶段油罐拱顶压力波动较大，之后趋于稳定;②随着氮气进口流量不断增加，油罐拱顶稳定压力随之增大，且增大速率越来越大;③油罐拱顶设计最大压力为2 000 Pa，考虑工程实际确定氮气最大进气速度 46.6 m·s-1，即进口流量为2 963 m3·h-1。

3  结 论

本文通过数值模拟的方式，采用湍流k-ε标准模型和PISO算法，研究了油罐氮气惰化过程中随氮气进口流量变化时，氧气体积分数分布和油罐拱顶压力变化规律，得出以下结论：

1）相同氮气进口流量下，油罐内氧气体积分数随时间不断降低，且刚开始降低速度较快，之后较为平缓。

2）工程实践中退役油罐惰化需要控制氧气体积分数安全临界值为4.56%。

3）氮气进口流量越大惰化所需时间越短。

4）为了保护退役油罐拱顶免受破坏，应限制氮气最大进口流量。

参考文献：

[1]DING X D，SONG W H，CHEN Z.The Causes and Consequ- ences Analysis of Fire and Explosion Accident Happened in Buried Oil Tank of Gas Station[C].2012 IEEE 19th International Conference on Industrial Engineering and Engineering Management， 2012.

[2]张迎新，吴强，刘传海，等. 惰性气体N2/CO2抑制瓦斯爆炸实验研究[J]. 爆炸与冲击，2017，37（5）：906-912.

[3]李恩田，谢磊，王树立.浮顶油罐罐顶油气惰化数值模拟[J].油气储运，2011，30（9）：671-673.

[4]张培理，杜扬，单锐，等. 进气口位置和进气体积流量对油罐油气惰化置换效率的影响[J].后勤工程学院学报，2012，28（3）：35-39.

[5]ANDRés Z， MENDIBURU J A D C. Method for determination of flammability limits of gaseous compounds diluted with N2 and CO2 in air[J]. Fuel，2018，226：65-80.

[6]胡文超，杜扬，张培理. 油气惰化抑爆研究进展[J]. 辽宁化工， 2019，48（8）：808-810.

[7]刘俊杰，邸振春，康健.惰性气体置换装置空间数学计算模型研究[J].广州化工，2017，45（11）：28-29.

[8]宋博，王卫强，孟凡力，等.CFD软件在油气储运工程领域的应用[J].当代化工，2015，44（2）：310-312.

[9] KING A T. A k–ε turbulence model based on the scales of vertical shear and stem wakes valid for emergent and submerged vegetated flows[J]. Journal of Fluid Mechanics，2012，701：1-39.

[10] 张宏飞，曹红松，赵捍东，等. 数值仿真中湍流模型的选择[J].弹箭与制导学报，2006（4）：242-244.

[11] JOHN D. ANDERSON J. Computational Fluid Dynamics The Basics with Applications[M].Beijing：Tsinghua University Press，2010.

[12]张培理，杜揚，欧益宏，等. 油罐油气惰化置换过程数值模拟研究[J].后勤工程学院学报，2010，26（3）：25-31.

[13]HE B， JIANG X， YANG G， et al. A numerical simulation study on the formation and dispersion of flammable vapor cloud in underground confined space[J].Transactions of the Institution of Chemical Engineers. Process Safety and Environmental Protection， Part B， 2017，107（12）：1-11.

[14]刘斌，丁欣硕. Fluent 17.0 流体仿真从入门到精通[M]. 北京： 清华大学，2018.

[15]刘文辉，蒋新生，何标，等. 氧气体积分数对油气爆炸特性的影响[J]. 后勤工程学院学报，2014，30（5）：47-52.

[16]李健铭.大型立式拱顶储罐结构应力分析与部件结构尺寸优化[D]. 新疆大学，2017.