竞争环境下红松单木树高与胸径的相对生长关系*
段光爽 王秋燕 宋新宇 张会儒 符利勇
(1.信阳师范学院数学与统计学院 信阳 464000;2.中国林业科学研究院资源信息研究所 国家林业和草原局森林经营与生长模拟重点实验室 北京 100091;3.河南农业大学信息与管理科学学院 郑州 450002)
木质生物质的形成是一个动态过程,源于顶端和径向生长的相互作用,其中,由顶端分生组织促进的顶端生长占主体,而维管形成层刺激次要的径向生长(Barton,2010;Groover,2010),这种相互作用从生态和进化论角度可解释树木如何适应自身环境(Bartholoméetal.,2013)。研究表明,顶端生长形成的树高与光照捕获高度相关(Molesetal.,2009),径向生长形成的树干粗细决定物质支持力度和水分运输效率(Niklas,1993;Bullock,2010;Mcmahon,1973),在特定环境下,单木树高随胸径生长的变化模式反映了该单木追求生长和遭遇生存中的一种权衡和妥协(Hulshofetal.,2015;Kingetal.,2006)。迄今为止,已有许多数学方程用于描述单木树高和胸径生长模式,常用来研究森林在不同环境条件下的结构特征,进而精准预测林分的生长收获量和碳储量(Feldpauschetal.,2011;Priceetal.,2007;Huangetal.,1992;Niklasetal.,2004;Henryetal.,2010)。
传统异速生长方程仅刻划了单木树高与胸径之间的函数关系,并未揭示其相互影响的内在机制,如树高生长如何影响胸径生长以及胸径生长如何影响树高生长。从遗传学理论出发,单木树高与胸径之间的关系主要由自身遗传因素决定,但树干顶端和侧生分生组织的资源分配也强烈依赖于单木生长条件,如自身各器官的相互影响、营养空间大小、相邻木竞争关系、立地质量和林分年龄等(Niklas,1995;Feldpauschetal.,2011;Ilomäkietal.,2003;Xuetal.,2016)。Sumida等(1997)基于阔叶混交林中青冈栎(Quercusglauca)生长数据研究发现,早期树高生长较快,而后期胸径生长相对较快。Trouvé等(2015)从林分密度、林木所处环境和水分胁迫角度阐明了岩生栎(Quercuspetraea)树高和胸径生长的分配规律。Hulshof等(2015)利用单木数据分析树高和胸径异速生长关系,发现影响单木树高和胸径异速生长关系的因子繁多,也较为复杂,传统异速生长方程很难准确揭示单木树高和胸径的生长规律。
博弈论(game theory)又称对策论,是研究相互依赖、相互影响的决策主体的理性决策行为以及这些决策的均衡结果的理论(Nash,1950;Fuetal.,2017)。在林分中,单木树高和胸径除受自身遗传因素影响外,还与相邻木存在互助或竞争关系,基于博弈论构建树高和胸径在外界环境影响下的相互竞争生长模型不仅可以量化单木树高与胸径生长之间的交互和协调作用,而且能够有效揭示树干木质生长动态的生态学机制(Fuetal.,2017)。尽管这有悖于潜在的生理机制,但单木树高与胸径生长的协同合作关系有助于树木更好地生存、发育生长和繁衍(Niklas,1995)。随着生长环境资源匮乏,单木会牺牲胸径生长而加快树高生长,或放缓树高生长而加强胸径生长,或牺牲树高生长而加强相邻木树高生长,或加强胸径生长而抑制相邻木树高生长等。在不同发育阶段,由于资源竞争,单木这种生长关系会达成不同的平衡(Sumidaetal.,1997))。按照达尔文进化论,在给定的环境下,单木会决定采用何种策略(竞争还是合作)实现生长最优化(Falsteretal.,2003),而博弈论构建的树高与胸径生长竞争模型能有效回答单木自身以及与邻近竞争木之间的树高和胸径相对生长关系。
红松(Pinuskoraiensis)为常绿针叶乔木,主要分布在我国长白山和小兴安岭一带。作为地带性顶极群落阔叶红松林的优势树种,红松具有重大的生态价值和经济价值,为促进阔叶林中红松人工更新,加速向阔叶红松林演替,有必要开展阔叶林中红松生长规律研究。因此,本研究在吉林省汪清林业局选择11块面积1 hm2的蒙古栎(Quercusmongolica)阔叶混交林样地共12 822株单木,基于博弈论并结合线性联立方程组构建以红松为对象木的不同树种树高与胸径生长竞争模型,探索红松单木生长受自身遗传和外部环境影响的资源分配规律,以期为阔叶混交林下红松更新和培育提供技术支撑。
1 研究区概况与研究方法
1.1 研究区概况
研究区位于吉林省汪清林业局塔子沟林场,130°05′—130°20′E,43°17′—43°25′N,属长白山系老爷岭山脉雪岭支脉,低山丘陵地貌,海拔300~1 200 m,坡度5°~ 25°。属季风性气候,年均气温3.9 ℃左右,年均降水量600~700 mm,且集中在夏季,占全年总降水量的80%。土壤以暗棕壤为主,平均厚度40 cm左右。植被属长白山植物区系,群落结构复杂,植物种类较多,主要树种有蒙古栎、白桦(Betulaplatyphylla)、红松、山杨(Populusdavidiana)、榆树(Ulmuspumila)、椴树(Tiliatuan)、黑桦(Betuladahurica)、长白落叶松(Larixolgensis)、色木槭(Acermono)、红皮云杉(Piceakoraiensis)、冷杉(Abiesfabri)、水曲柳(Fraxinusmandshurica)、黄檗(Phellodendronamurense)等。
1.2 数据收集
数据采集自2013年布设于汪清林业局塔子沟林场的11块蒙古栎阔叶混交林样地,每块固定样地面积均为100 m × 100 m。利用罗盘仪,将样地划分为100 个10 m ×10 m 的网格单元,在每个网格单元内对胸径1 cm以上的树木进行每木检尺,记录树种,测量胸径(D)、树高(H)、枝下高、冠幅(东西南北4个方向)等因子,并用激光测距仪测定单木坐标(X,Y)。为了人工促进更新,汪清林业局于2003年在11块阔叶混交林中补植了大量红松幼苗。本研究共调查单木12 822株,根据研究目的,将其分为红松(3 927株)、蒙古栎(2 890株)、其他阔叶树种(4 188株)和其他针叶树种(1 817株)4种类型。本研究对象是红松单木(处于幼龄林阶段),共计3 661株。样木统计量见表1,4种类型竞争木以及各样地树高(H)与胸径(D)散点关系见图1。

图1 树高与胸径的散点分布Fig.1 The scatter distributions of tree height and DBH
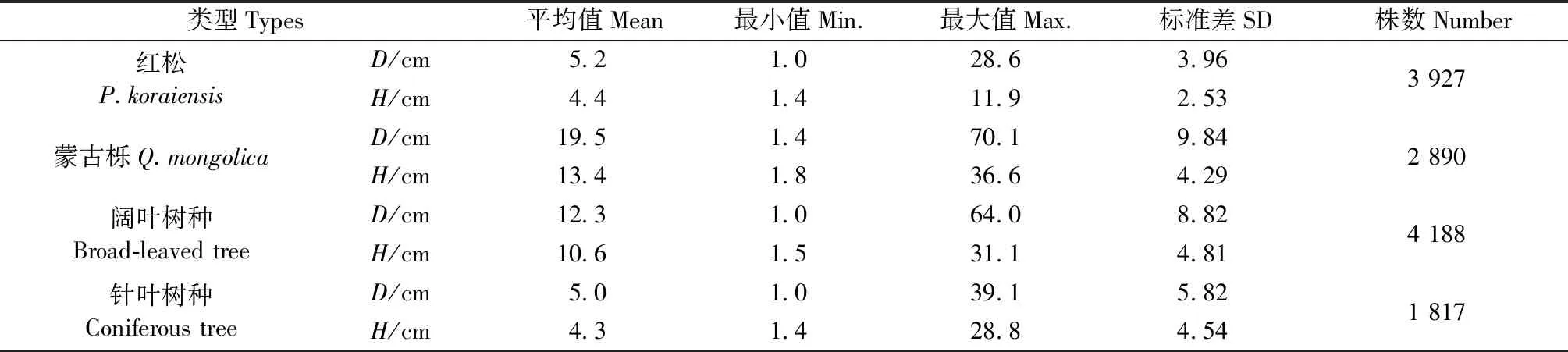
表1 4种类型竞争木的单木数据统计Tab.1 Summary statistics of individual stand for 4 species types
1.3 树高与胸径生长竞争模型

(1)
式中:H和D分别表示红松单木树高和胸径;Li(i=1,…,4)表示第i类树种与对象木红松单木的加权平均距离;Di(i=1,…,4)表示第i类树种的加权平均胸径;Hi(i=1,…,4)表示第i类树种的加权平均树高;i=1表示竞争木为红松,i=2表示竞争木为蒙古栎,i=3表示竞争木为其他阔叶树种,i=4表示竞争木为其他针叶树种;aH和λD分别表示树高和胸径的截距项;bH、βD、ai、λi、bi、γi、ci和βi(i=1,2,3,4)为回归系数,分别表示对象木红松单木和4种类型竞争木的加权距离、胸径和树高对红杉单木树高和胸径的影响速率;ε=(εH,εD)T表示联立方程组中树高和胸径方程的随机误差,服从ε~N(0,Φ),其中Φ=σ2ψ,ψ为偏差ei的误差结构矩阵,σ2为随机误差的方差。
模型(1)可分解为2部分:
(2)
式中:Ha和Da表示独立环境下红松单木树高与胸径的相对生长状况;Hb和Db表示竞争环境中竞争木影响下红松单木的生长状况:
(3)
(4)
其中,
(5)
1.4 模型参数含义
模型(1)中参数符号和量级决定单木树高(H)与胸径(D)生长状态的作用方式和强度(Fuetal.,2017),用策略矩阵表示,见表2。

表2 树高与胸径间的6类相互作用Tab.2 The six types of interactions between tree height and DBH
由表2可知,根据树高(H)与胸径(D)的不同策略选择,共构成6类相互作用(Kimmins,2005),其中,3类正相互作用为:1) 互利共生,树高(H)与胸径(D)相互受惠;2) 原始协作,树高(H)与胸径(D)没有明显的互惠互利;3) 偏利共生,树高(H)与胸径(D)其中有一受惠,另一无影响;3种负相互作用为:4) 竞争关系,树高(H)与胸径(D)均受阻;5) 寄生关系,树高(H)与胸径(D)其中有一受惠,另一受阻;6) 偏害共生,树高(H)与胸径(D)其中有一受阻,另一无影响。
根据模型(1)参数估计值可量化每一交互作用的程度,进而衡量红松受自身遗传因素或外界环境影响的生长状况。参数取值正负符号暗示这种相互作用是加强或减弱红松D或H的生长能力,如果参数值不显著,表明该交互作用不影响红松D或H的生长。因此,模型(1)能有效反映红松在自身内部机制和外界环境干扰下树高(H)或胸径(D)的生长分配策略。
1.5 参数估计
选用最小二乘法(OLS)和似乎不相关回归法(SUR)估计模型(1)参数。最小二乘法计算速度较快,但收敛性较差,似乎不相关回归法方法计算速度较慢,但收敛性较好。
对于似乎不相关回归法,其基本思想为:首先令误差结构矩阵ψ=I,通过最小化函数
(6)
(7)

(8)
估计模型参数。

对于最小二乘法,采用最小化目标函数式(6)得到模型参数估计值。
1.6 模型评价
(9)
(10)
(11)
(12)
(13)
胸径对应的评价指标计算方法与树高相似。
为了准确反映模型预测精度,采用1阶交叉检验法,即每次先用10块样地数据估计模型参数,然后对剩余1块样地数据进行预测,共重复11次,最终预测出来的树高(H)和胸径(D)用于计算各评价指标。
本研究所有计算均在R中实现,其中线性联立方程组采用systemfit包进行计算。
2 结果与分析
2.1 模型拟合
基于11块蒙古栎阔叶混交林最终提取的3 176株红松(横坐标和纵坐标均介于5 ~95 m之间)以及相应的竞争木数据,利用最小二乘法和似乎不相关回归法对模型(1)进行拟合,模型参数估计值及检验结果见表3。比较发现,2种参数估计方法得到的估计值差别不大,就显著性程度来说,仅L1、H42项的系数λ1、β4不同。通过表3各参数估计值可以得到:

表3 模型(1)参数估计及其显著性检验①Tab.3 The parameter estimates and significance testing of model(1)
1) 截距项aH为正、λD为负,显著性均很强,表明现实林分整体环境是优先分配红松树高(H)生长,抑制胸径(D)生长;
2) 斜率项bH、βD均为正,表明在独立环境下红松自身树高(H)与胸径(D)是相互促进的;
3) 变量L、D、H的系数对应4种类型竞争木的符号相同(仅λ4发生改变,但并不显著),反映不同类型竞争木的L、D、H对红松影响一致;
4)ai(i=1,…,4)为负、λi(i=1,…,4)为正,表明周围竞争木的距离(L)抑制红松树高(H)生长,但促进其胸径(D)生长,原因在于红松早期生长需要一定的蔽荫性;
5)bi(i=1,…,4)为负、γi(i=1,…,4)为正,表明周围竞争木的胸径(D)抑制红松树高(H)生长,但促进胸径(D)生长;
6)ci(i=1,…,4)为正、βi(i=1,…,4)为负,表明周围竞争木树高(H)的作用正好与胸径(D)相反,原因在于竞争,优先获取同质资源。
从红松单木周围竞争木树种类型上看,参数估计值显著程度可得出:1) 针叶树种L、D、H的系数均不显著,仅最小二乘法下的β4显著,且似乎不相关回归法下均不显著,反映针叶树种对红松胸径(D)和树高(H)影响不大,可能是邻近木较少,大多数样地针叶树偏少甚至没有;2) 蒙古栎L的系数均不显著;3) 阔叶树种D的系数均不显著。
2.2 模型检验
为衡量参数的稳定性并比较最小二乘法和似乎不相关回归法的有效性,采用交叉检验,结果见表4。由表4可知,总体而言,模型(1)拟合效果整体良好。最小二乘法(OLS)拟合结果略优于似乎不相关回归法(SUR),单从RMSE来说,树高(H)和胸径(D)后者仅比前者多0.035 9和0.021 6,相应百分比仅为3.51%和1.30%,这种差异可忽略不计。

表4 模型(1)的评价指标Tab.4 Evaluation indices for model(1)
2.3 基于博弈论的红松单木树高与胸径竞争关系
基于博弈论,并结合模型(1)中各变量线性参数的显著程度,得到红松单木树高与胸径生长的相互作用关系,见表5。

表5 红松单木树高与胸径竞争关系Tab.5 The competitive relationships between tree height and DBH of young aged P.koraiensis
由表5可知:1) 内在因素方面,截距项体现寄生关系,而斜率项表明互利共生关系,进一步反映红松单木为适应蒙古栎阔叶混交林环境选择优先分配树高(H)生长的策略,而自身2个特征树高(H)和胸径(D)又是相互促进的;2) 外在因素方面,分4种类型:其一,红松属于种内竞争,3个因素距离(L)、胸径(D)和树高(H)均体现出寄生关系,即牺牲某一特征生长而促进另一特征生长,说明种间竞争是比较强烈的;其二,蒙古栎的距离(L)暗示偏利共生或原始协作关系,反映红松生长资源分配依赖于距离,而树高(H)与胸径(D)体现寄生关系,这正是红松对同质资源竞争的一种正常策略;其三,阔叶树种的距离(L)和树高(H)体现寄生关系,而胸径(D)表明原始协作关系;其四,针叶树种的距离(L)和树高(H)表明偏害共生或原始协作关系,而胸径(D)表明原始协作关系。
3 讨论
单木树高(H)与胸径(D)的异速生长关系反映该单木生长过程中的一种权衡和妥协,而将单木生长过程看成一个具有树高和胸径2种成分的生态系统可以更好地阐述这种权衡,其根据内在遗传和外在环境进行互动和协作(Sumidaetal.,1997),单木异速生长反映单木在树高(H)和胸径(D)上的资源分配策略(Priceetal.,2007)。红松单木在蒙古栎阔叶混交林中的生长状况,不仅体现了自身内部遗传因素的生理机制,而且响应了周围环境变化的影响。本研究通过构建树高(H)与胸径(D)生长竞争模型来揭示蒙古栎阔叶混交林下红松幼龄阶段资源分配在树高(H)和胸径(D)生长的交互作用规律,将这种相对生长关系分解为2部分:自身内部生理机制决定的独立生长和源于生长环境种间或种内树种的干扰(Henryetal.,2010)。基于3 176株红松及其竞争木相关数据,模型(1)的决定系数(R2)高达0.847 3和0.845 6(似乎不相关回归法为0.839 7和0.838 0),模型(2)的决定系数(R2)为0.825 2和0.825 2(似乎不相关回归法为0.817 7和0.817 7),模型(3)的决定系数(R2)为0.126 9和0.162 3。从2个模型的贡献率对比来看,遗传的生理机制发挥主要作用,而外界环境的干扰影响较小,表明蒙古栎阔叶混交林适合红松生长。
基于博弈论的红松单木生长竞争关系表明:11块蒙古栎阔叶混交林整体环境适合红松单木资源优先分配树高(H)生长,与幼树生长规律一致(卢军等,2015),而自身树高(H)与胸径(D)呈现互利共生关系,表明红松自身遗传生理机制得到充分发挥。外界环境中竞争木的距离对树高(H)具有抑制作用,进一步验证红松早期生长需要一定的庇荫;竞争木的胸径(D)和树高(H)大多体现寄生关系,即竞争木胸径促进对象木胸径生长,竞争木树高促进对象木树高生长,反映了单木对同质资源的一种普遍竞争规律(Kimmins,2005)。内外因素共同反映了蒙古栎阔叶林适合红松幼苗更新与发育。
红松内部之间单木相互影响较大,即L1、D1、H1的系数均非常显著,而其他针叶树种对红松对象木的影响微乎其微,即L4、D4、H4的系数不显著。3 176株对象木红松的竞争木株树分布见表6,对象木红松周围红松较多而针叶树种较少,且二者平均胸径均很小(红松5.2 cm,针叶树种5.0 cm,见表1),说明红松单木呈现聚集情况,彼此之间已经存在对资源的竞争,为了捕获更多光照红松单木选择优先分配树高生长的策略。红松与其他针叶树种之间还未构成竞争。

表6 红松的竞争木分布Tab.6 The distribution of competitive tree of P.koraiensis
为了探索竞争半径对蒙古栎阔叶混交林下红松相对生长关系的影响,本研究分别以对象木红松半径3 m和8 m选取竞争木,相应树高(H)与胸径(D)生长竞争模型的计算结果及其对应的红松相对生长竞争关系表明,与对象木红松半径5 m相比,红松树高(H)与胸径(D)生长资源分配所反映的内部生理机制一致,而外部环境影响整体上相似,差异体现在其他针叶树种的树高,随着竞争半径扩大,其他针叶树种干扰红松生长,其竞争关系由原始协作转为寄生关系。
4 结论
基于博弈论,本研究提出一个概念框架描述单木胸径(D)和树高(H)如何通过相互联系来调节其功能,从而实现竞争与合作。所构建的树高(H)与胸径(D)生长竞争模型不仅可有效描述单木异速生长情况,而且将这种生长细分为独立不受影响的作用和周围环境交互式干扰作用,从而量化了竞争与合作对单木生长的影响。这种结合博弈论思想的单木树高与胸径相对生长方式,再一次揭示了竞争与合作的生物学上的协调性(Scarano,2002)。
单木生长对资源供应的敏感性不仅体现在生长数量上,还表现在异速生长模式上(Fuetal.,2017)。本研究构建蒙古栎阔叶混交林下红松单木树高(H)与胸径(D)生长竞争模型,利用博弈论解释了其相对生长模式,从内部遗传上得出红松树高(H)与胸径(D)是互利共生的,而外部环境上,红松、蒙古栎和其他阔叶树种的影响体现出寄生关系,针叶树种无影响,呈现原始协作关系。通过模型检验和红松竞争木的不同选择方式,进一步说明树高(H)与胸径(D)生长竞争模型在处理红松相对生长关系上的稳健性。综上所述,蒙古栎阔叶混交林适合红松生长。
——低维护的小型观赏草阔叶山麦冬

