浅谈定积分、二重积分与三重积分求体积
刘余娇
(绵阳师范学院数理学院,四川绵阳 621000)
0 引言
定积分是定义积分区间上的积分,其应用很广泛,可以求面积、平面曲线弧长及几何体的体积[1].而二重积分是定义在平面区域上积分,其几何意义是以定义域区域D为底面及定义域上的函数z=f(x,y) 对应的曲面为顶的曲顶柱体的体积的代数值,对于多个曲面所转成的立体的体积即为多个曲顶柱体体积的代数和.而三重积分是三元函数定义在空间几何体Ω上的积分.几何意义上是定义在几何体上的密度函数与该几何体体积的积所得该立体的质量,即三重积分就是质量,其实这个密度就是体密度,密度×体积=质量,在特殊情况下如果密度函数总为1,那么体积=质量[2].
1 预备知识
为了更好地理解重积分的应用,首先给出二重积分的几何意义及三重积分的相关性质.
1.1 定积分求体积

1.2 二重积分的几何意义及性质
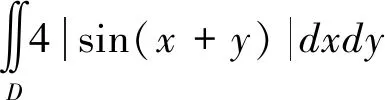
若f(x,y)0则二重积分的几何意义就是以f(x,y) ) 为顶,以D为底且在xoy下方的曲顶柱体体积的负值.
若f(x,y)在D的若干部分区域为正,而在其他区域为负,那么二重积分等于上方体积减下方曲顶柱体的体积.
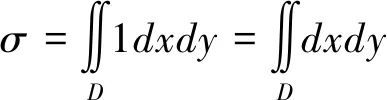
1.3 三重积分的几何意义与性质
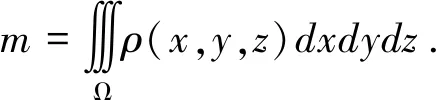

2 如何利用重积分求体积
2.1 二重积分求体积
二重积分的本质:曲顶柱体体积.二重积分是二元函数z=f(x,y),(x,y)∈D.在平面区域D上的积分,同定积分类似,是某种特定形式的和的极限.曲顶柱体的顶为连续曲面z=f(x,y),(x,y)∈D.则其体积为

而对于任意其他不规则的立方体几何体,在求其体积时,总可以分割成若干个曲顶柱体体积的代数和[6].例如,由两曲面z1=f1(x,y),(x,y)∈D及曲面z2=f2(x,y),(x,y)∈D(其中D
该几何体在在xoy平面上的投影,设z1≥z2)所围成的几何体的体积为[8]27
上例中,由两个曲面所围成的空间几何体的体积,即可视为两个曲顶柱体的体积相减.因此,只要会求曲顶柱体的体积,即能求任意空间立体几何体的体积.
2.2 三重积分求体积
三重积分的本质:三重积分就是立体的质量.当积分函数为1时,就是其密度分布均匀且为1,质量就等于其体积值.当积分函数不为1时,说明密度分布不均匀.


在上例中,如利用三重积分计算由两曲面z1=f1(x,y)及曲面z2=f2(x,y)所围成的几何体的体积,因z1zz2,故有
由上式可以看出,对于同一个空间立体几何体求体积,不管是二重积分还是三重积分求体积,其实质的意义及最终的结果都一样,只是所采用的方式不同.
例分别利用定积分、二重积分与三重积分求由下面两曲面

方法一:利用定积分已知截面面积求体积.
如右图所示,对于固定的z,当0 Dz={(x,y)|x2+y26-z}; 方法二:利用二重积分求体积. 方法三:利用三重积分求体积 对于一个由光滑曲面所转成空间立体几何体,特别是对于垂直于一定轴的截面的几何体,其体积可以分别采用定积分、二重积分及三重积分来求解,只是思考问题的途径不同.但采用三重积分计算时,须适当地选取坐标系,最后又能转换成与二重积分相同的二重积分计算式,即在计算三重积分时,由三重积分转换成二重积分的形式和之前直接利用二重积分列的式子是完全相同的.因为在解三重积分时,都是先转换成二重积分的,再转换成定积分进行计算的.虽然二者的几何意义不同,但从某一个角度上来说,两者是相通的.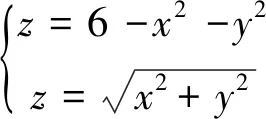
3 结论

