节点属性和拓扑信息相结合的脑网络聚类模型 *

肖继海，崔晓红，陈俊杰

(太原理工大学信息与计算机学院，山西 晋中 030600)

1 引言

近年来，图挖掘已经成为一个热门的研究领域并应用到社交网络、计算生物学及计算机网络的分析中。此外，许多新的数据也可以表示为图，如功能性磁共振大脑影像数据fMRI(functional Magnetic Resonance Imaging)。本文利用受试者的fMRI数据，构建脑网络，其中每个节点代表一个脑区，每条边代表2个脑区之间的功能连通性[1]。这些脑网络为探索人脑的内部结构和活动提供了一个新的视角,同时也可为脑疾病临床诊断提供有价值的辅助信息。

目前的研究大都集中于脑疾病的分类，例如，Huang等人[2]提出了一种基于树引导的组稀疏学习多频带脑网络分类模型，首先在多频带中获取低频振幅比率数据，使用基于树的稀疏学习方法进行特征选择，最后结合多频段特征进行分类。Liu等人[3]从T1加权MRI(Magnetic Resonance Imaging)图像和DTI(Diffusion Tensor Imaging)图像中提取8个特征集，并采用两步特征选择方法得到最具鉴别性的特征，最后采用基于多特征集的多核SVM学习方法对精神分裂症SZ(SchiZophrenia)患者和正常人NC(Normal Control)进行分类。杨勇哲等人[4]提取结构和静息态功能磁共振图像的90个感兴趣区域的灰质体积、局部一致性、低频振荡振幅和度中心性作为特征，使用基于递归特征消除的支持向量机对脑疾病患者和正常人进行分类。

以上研究旨在选择特征来训练分类器，以实现对数据的自动分类。当训练数据样本量足够大并且选择了最优特征时，分类性能通常很好。但是，从大量的数据中提取和选择最优的特征很费时。此外，在许多实际情况下，只能获取到较少的标记数据样本。因此，在有限的标记数据样本上找到有显著差异的特征是不可靠的。

针对以上问题，本文提出了一种节点属性和拓扑信息相结合的脑网络聚类模型。与分类相反，聚类的不同之处在于不需要数据的类型标签[5]。脑网络聚类的目的是根据脑网络之间的相似程度自动聚类，类内脑网络之间具有较高的相似性[6]。

该方法主要的挑战是如何准确计算脑网络之间的相似度。目前，文献[7]调查了48名SZ患者和24名健康对照者的全局和节点网络特性，发现精神分裂症患者的大脑网络特性与健康人的相比有显著差异，比如SZ患者的平均介数中心性较高。另外，文献[8]发现SZ患者功能性磁共振网络的拓扑和空间结构被显著破坏。以上文献表明，SZ患者的脑网络在节点属性和拓扑结构上都存在显著差异。因此，为了更全面地捕获脑网络的差异，本文从节点属性和拓扑结构两方面测量脑网络的相似度。首先，选择目前研究公认的SZ患者存在异常功能连接的默认模式网络DMN(Default Mode Network)[9,10]作为感兴趣区域构建脑网络，然后分别使用余弦相似度和子网络核来度量脑网络的属性相似度和结构相似度，接着将结构相似度和属性相似度集成为一个相似度矩阵，最后利用谱聚类实现脑网络聚类。

2 脑网络聚类模型

脑网络聚类模型如图1所示，包含fMRI数据的预处理、标记DMN、构建相应脑网络、计算脑网络的相似度以及聚类。也就是，逐一对每个脑网络的fMRI数据先实施预处理，找到DMN对应的脑区并构造脑网络，随后计算其属性相似度和结构相似度，最后整合2种不同类型的相似度，并使用谱聚类方法对脑网络进行聚类。

Figure 1 Brain network clustering model图1 脑网络聚类模型

2.1 预处理数据

使用DPARSF(Data Processing Assistant for Resting-State fMRI)工具包对fMRI图像数据进行预处理，包括删除前10个时间点数据、时间片的校正和头动的校正。本文使用DARTEL(Diffeomorphic Anatomical Registration Through Exponentiated Lie algebra)配准方法将数据配准到标准空间，期间将数据重新采样为3×3×3 mm3体素，再进行平滑处理以去除协变量的影响，最后，进行滤波去噪，频率范围为[0.01,0.08] Hz，以减少高频和极低频生理噪声的影响，这样能较好地反映神经元自发活动。

2.2 标记DMN并构建功能脑网络

研究已证实，在静息态功能脑网络中默认模式网络(DMN)能保持相对稳定的状态，通过它可以研究功能脑网络连接的异常[10 - 12]。本文使用自动化解剖标记AAL(Automated Anatomical Labeling)图谱[13]，从中找到DMN所包含的32个脑区(左右脑)，脑区名称如表1所示。

Table 1 Brain regions included in the DMN

脑网络的节点由表1中的32个脑区定义，节点的时间序列取脑区内所有体素时间序列的平均值，节点之间的连接权值由节点时间序列间的皮尔逊相关系数定义，加权全连接网络由此形成。为了避免传统二值网络构建过程中产生的偏差，使用Kruskal算法[14]将加权全连接网络转换成无偏差的脑网络，最终形成最小生成树无偏DMN脑网络。

2.3 测量脑网络相似度

脑网络不仅具有全局拓扑结构特征而且还具有局部属性特征。为了综合评价脑网络的相似度，本文将上述2方面特征结合起来测量脑网络相似度，流程图如图2所示。图2中，G和H为脑网络，S(G,H)为脑网络G和H的相似度，Satt(G,H)为G和H的属性相似度，Sstr(G,H)为G和H的结构相似度，δ为权重。

Figure 2 Flow chart of similarity measurement in brain network图2 脑网络相似度测量流程图

(1)节点属性相似度的测量。

介数属性是复杂网络的一个重要特征。节点介数越大，表示该节点是中枢节点，对整个网络的信息传输起到很大的作用。研究表明[15]，SZ患者的大脑中枢受到破坏，在临床应用中，介数常用于健康人和SZ患者脑网络的比较。因此，本文使用节点的介数来表征脑网络的局部属性，脑网络间属性相似度由脑网络中所有节点介数之间的相似度来评价。通过节点i的所有最短路径的数量定义为节点i的介数bci，计算如式(1)所示：

(1)

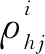
属性相似度Satt(G,H)使用余弦相似度计算，如式(2)所示：

(2)

其中,bcm(H)表示脑网络H中第m个节点的介数，bcm(G)表示脑网络G中第m个节点的介数，n表示脑网络中节点总数。

(2)拓扑结构相似度测量。

一组对象之间的相似性可以用核函数来度量。当用核函数处理图数据时，该核称为图核，图核是把图数据从原始的图空间映射到特征空间，使得2幅图像的相似性就是它们在特征空间中的点积。因此，2幅图之间的相似性可通过图核来度量[16]。

大脑网络与图的主要区别是大脑网络中每个节点的唯一性，也就是说，大脑网络中的每个节点都表示特定的大脑区域，是大脑网络的一个特定特征。因此，本文采用子网络核(Sub-network Kernel)[17]测量脑网络间的拓扑结构相似度。与传统意义上的图核相比，子网络核的一个重要特性就是能捕获网络节点上的多层次拓扑性质，而且还兼顾了网络中各个节点的唯一性。子网络核的构建过程简要描述如下：

①在每个网络节点上构建一组子网络，以便反映脑网络在多层次上的连通性。

G=(V,E)和与H=(V,E′)表示一对脑网络，其中V代表脑网络的节点集，E和E′分别表示G与H的边集。各个脑网络拥有相同的大脑区域，即它们有相同的节点。为了表达脑网络的多级拓扑特性，需要在网络G与网络H的每个节点vi上分别定义2组子网络：

(3)

(4)

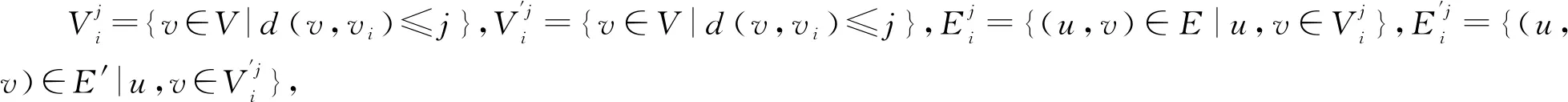
由式(3)和式(4)可知，对于由n个节点组成的脑网络，可以得到n组子网络：

(5)

(6)

②网络G与H中同一节点的相似度就是2个网络中同一节点的所有子网络的相似度，如式(7)所示：

(7)

(8)

(9)

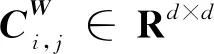
(10)

③因此，脑网络G与H的图核就是脑网络中所有节点对应子网络对的相似度，n表示脑网络中的节点数目，G和H的图核如式(11)所示：

(11)

④最后得到2个脑网络G与H的图核即为2个脑网络G与H之间的拓扑结构相似度，如式(12)所示：

Sstr(G,H)=k(G,H)

(12)

(3)脑网络的相似度。

为了全面评价脑网络之间的相似度，本文将脑网络之间属性方面的相似度与结构方面的相似度进行优化组合。

首先，因为属性相似度与结构相似度的类型不同，故在组合二者之前必须归一化，如式(13)所示：

(13)

其中，Snorm(G,H)是脑网络G与H归一化之后的相似度，S(G,H)是脑网络G与H的相似度。

然后，通过权重δ来调整2种相似度的贡献程度，使组合最优。

脑网络G与H的相似度定义如公式(14)所示：

SG,H=δSatt_norm(G,H)+

(1-δ)Sstr_norm(G,H)

(14)

其中，Satt_norm(G,H)是功能脑网络G与H归一化后的属性相似度，Sstr_norm(G,H)是功能脑网络G与H归一化后的结构相似度，δ是权重参数。

第三步，脑网络之间的相似矩阵S定义如下：

(15)

其中,SG,H是脑网络G与H之间的相似度，N是脑网络数量。

2.4 脑网络聚类模型描述

前文已经构造出脑网络的相似矩阵S，这样可以方便地将脑网络的聚类问题转化成谱聚类[19]问题，将相似度高的脑网络自动归为一类。聚类模型的基本过程描述如下：

输入：N个脑网络。

输出：向量Y，若向量Y的第i个元素为cj，则表示第i个被试对应的脑网络归属到类cj中。

步骤1将脑网络的相似矩阵S置为N×N零元矩阵，N表示脑网络数目；

步骤2对N个脑网络依次计算每个节点的介数；

步骤3由式(2)得到N个脑网络之间的属性相似度；

步骤4对N个脑网络执行子网络核算法，得到N个脑网络之间的结构相似度；

步骤5将属性相似度和结构相似度归一化，由式(14)与式(15)得到相似矩阵S；

步骤6定义对角阵D，其元素D(i,i)为相似矩阵S的第i行元素之和；

步骤7定义矩阵L=D-1/2SD-1/2;

步骤8求矩阵L的m个最大特征向量x1,x2,…,xm，按列存放m个特征向量产生矩阵X=[x1,x2,…,xm]∈Rn×m；

步骤9将矩阵X的每一行标准化，得到矩阵Y；

步骤10将矩阵Y的每一行作为Rm中的一个点，执行K-means算法将这些点聚成m个类。

3 实验数据与结果

3.1 实验数据

本文实验的数据来自于openfMRI数据库(https://www.openfmri.org/)，经筛选，满足数据收集条件的有99名，其中包含50名SZ患者与49名正常对照组。扫描参数：TR(Repetition Time)重复时间为2 000 ms；TE(Echo Time)回波时间为30 ms；翻转角度为90°；切片厚度为4 mm；切片数量为34；时间点数为152个。被试的基本信息统计情况如表2所示。

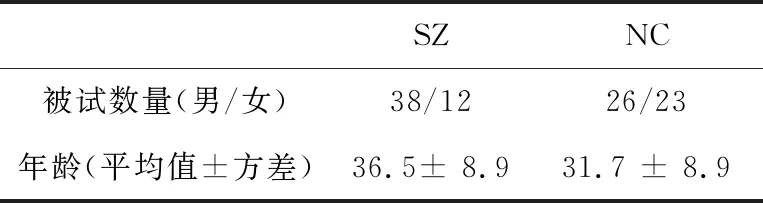
Table 2 Statistical table of basic information of subjects

3.2 实验参数设置

实验中，因为仅有2个可能的标签(SZ，NC)，故将类别数m设置为2。在子网络核算法中，参数t与d分别设置为3与3。权重δ通过网格搜索法来优化，δ初始值是0.1，步长是0.1，最大值是0.9。

3.3 无偏脑网络

为了构建合理的脑网络，本文脑网络的节点由DMN包含的32个脑区定义，节点之间的连接权值由节点时间序列间的皮尔逊相关系数定义。使用Kruskal算法得到SZ与NC所有被试的无偏脑网络。SZ(No.01)与NC(No.01)的无偏脑网络如图3所示。从图3中看出，SZ患者和正常人的大脑在额叶、颞叶和顶下小叶之间的功能连接存在明显的差异。

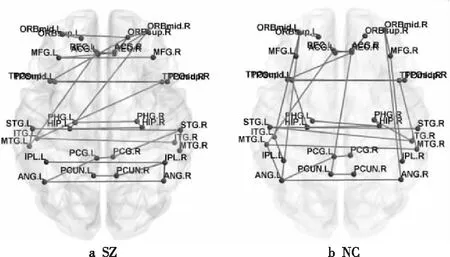
Figure 3 Unbiased brain network of SZ and NC图3 SZ与NC的无偏脑网络

3.4 相似矩阵

谱聚类的关键在于相似性度量。脑网络构建后，脑网络之间的相似度通过整合脑网络在属性与结构2方面的相似度来综合评价。本文首先使用余弦相似度来计算脑网络间的介数属性相似度，脑网络的属性相似度矩阵如图4所示；其次，使用子网络核来度量脑网络间的结构相似性，其相似度矩阵如图5所示；最后，选择最优权重参数δ，将属性相似度与结构相似度进行优化组合，得到最终相似度矩阵，如图6所示。

Figure 4 Attribute similarity matrix图4 属性相似度矩阵

3.5 聚类性能

将属性相似度矩阵与结构相似度矩阵按一定比例优化组合，形成最终相似度矩阵。然后通过谱聚类[20]完成上述脑网络的聚类。通过以下指标来评估聚类方法的性能： Rand指数、召回率、精确率和F-measure[21]。为准确评价上述指标，实验中要求重复运行程序50次，将其平均值作为最终的性能评价结果。

Figure 5 Structural similarity matrix图5 结构相似度矩阵

Figure 6 Final similarity matrix图6 最终相似度矩阵

(1)Rand指数表示正确聚类的百分比，Rand指数越大，意味着聚类结果与真实情况越吻合。

Rand指数由式(16)计算：

(16)

其中,TP是真正类的个数，TN是真负类的个数，FP是假正类的个数，FN是假负类的个数。

(2)召回率(Recall)表示在被识别为正类别的样本中，真实情况是正类别的比例，即查全率，由式(17)计算：

(17)

(3)精确率(Precision)表示在所有正类别样本中，被正确识别为正类别的比例，即查准率,由式(18)计算：

(18)

(4)F-measure综合了精确率和召回率的结果，是精确率与召回率加权调和平均值。F-measure由式(19)定义：

(19)

其中,P表示精确率，R表示召回率。在本文中，使用F1(β=1)评价聚类的性能。当F1的值较高时，则说明聚类模型的效果比较理想。

为评估本文所提方法SA-cluster(Structure Attribute-cluster)的聚类性能，在相同数据集上设计实验,将本文的方法与2种方法进行比较：

(1)基于介数属性的谱聚类算法(A-cluster)：构造基于介数属性的相似矩阵，将相似矩阵输入谱聚类模型，对脑网络进行聚类。

(2)基于结构的谱聚类方法(S-cluster)：构造基于拓扑结构的相似矩阵，将相似矩阵输入谱聚类模型，对脑网络进行聚类。

相同数据集上3种方法的聚类性能如表3所示。结果表明，本文方法(SA-cluster)的聚类性能最好，其Rand指数是0.91，精确率是0.86，召回率是0.98，F1是0.92。

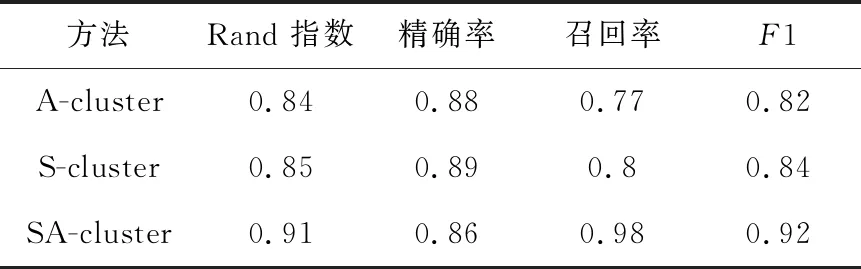
Table 3 Clustering performance of three methods

4 实验结果讨论

4.1 聚类性能的比较

如表3所示，本文方法在Rand指数、精确率、召回率和F1方面表现最出色。3种方法中，A-cluster方法使用脑网络的介数属性计算每对脑网络之间的相似性，并用于聚类。A-cluster方法的Rand指数与召回率比较低，这说明该方法不能较准确地识别出SZ患者，存在漏诊。结果表明，仅仅从局部属性角度不能准确反映脑网络之间的相似性。

S-cluster通过在脑网络上执行子网络核算法来得到相似矩阵。从表3可以看出，与A-cluster方法相比，该方法的聚类结果有所改善，查准率和查全率提高了，漏诊率下降，能较准确地识别出患者。结果说明，当网络的局部属性发生变化时，网络的全局连接结构也受到影响。因此，全局结构的相似性描述方法对聚类有很大贡献。

与前2种方法相比，本文方法(SA-cluster)的Rand指数是0.91，精确率是0.86，召回率是0.98，F1是0.92，准确率和查全率最高，漏诊率最低，更能准确地识别出患者，聚类的效果比较理想。这主要是因为节点属性和拓扑结构从不同的角度描述脑网络的相似度，将两者有效地结合可以更好地表达脑网络之间的相似度。这一结论正好与文献[7,8]的研究结果一致，进一步证实了SZ患者的大脑网络在节点属性和拓扑结构上与正常人的脑网络存在差异。

基于上述分析，本文方法巧妙地整合了属性相似度与结构相似度，其中以介数属性相似度来刻画脑网络的局部特征，以结构相似度来刻画脑网络的全局拓扑结构特征。特别地，本文使用子网络核算法来度量脑网络的拓扑结构相似性，该算法不仅考虑到脑网络中每个脑区节点的唯一性，而且还能够捕获到脑区节点的多级拓扑特征，这一点对于脑网络的相似性度量非常重要。可以看出，属性特征与内部节点拓扑结构对图聚类具有重要意义。因此，基于属性与结构相结合的相似性度量方法可以更准确地刻画脑网络的相似性，从而有效提高聚类性能。

4.2 参数δ对聚类性能的影响

权重参数δ用于调整属性相似度与结构相似度的贡献程度。为分析权重参数δ对本文方法聚类性能的影响，本文为参数δ设置了不同的值，δ初始值是0.1，递增步长是0.1，终值是0.9。参数δ取不同值的聚类结果如图7所示。

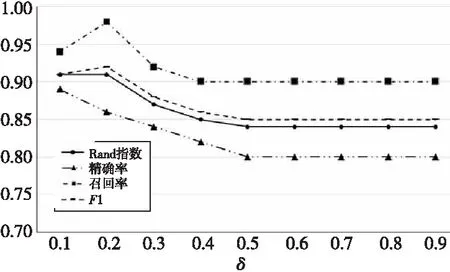
Figure 7 Influence of different δ values on clustering performance图7 参数δ不同取值对聚类性能的影响

图7表明，无论δ取何值，Rand指数、精确率、召回率和F1值都在0.8以上，说明从属性和结构2方面能较准确地衡量脑网络相似度，脑网络的拓扑结构和属性特征对脑网络的聚类起着重要作用。当δ取值为0.2时，聚类性能最好，其Rand指数为0.91,精确率为0.86,召回率为0.98,F1值为0.92，这说明在相似度的计算中，结构相似度贡献较大。

5 结束语

本文提出一种节点属性和拓扑信息相结合的脑网络聚类模型。首先，使用余弦相似度来计算脑网络之间的属性相似度，然后，使用子网络核来度量脑网络之间的结构相似度，最后，将属性相似度与结构相似度相结合，得到相似度矩阵，并用谱聚类算法聚类。实验结果表明，本文提出的聚类模型在Rand指数、召回率、精确率和F1值方面都表现较优。