基于SCILAB的多精度算法研究与实现 *

兰 静，刘文超，姜 浩,林文强

(1.重庆工商大学融智学院，重庆 404100；2.国防科技大学计算机学院，湖南 长沙 410073)

1 引言

高性能处理器被广泛应用于信息化联合作战、航空航天、模拟核试验、气象预报和抢险救灾等领域。近年来，我国自主研发的处理器发展迅速，这对于我国的国家安全具有重要意义，有利于完善我国经济信息系统以及国防领域的安全和保密问题。随着计算机技术的不断发展，高端计算已经开始从单一追求高性能转变为致力于综合高效能的提升，以解决当前高性能计算领域所面临的实用性能和可编程性问题。浮点数运算对于计算机性能影响显著，在浮点运算过程中存在舍入误差，计算规模较小时，这些误差不会造成明显影响。现代科学工程计算一般涉及到大规模计算，在这种大规模、长时程的数值计算中，由于舍入误差的累积效应存在，可能导致数值计算结果不准确、不可靠，甚至得到完全错误的结果。高精度算法库的设计和实现，是解决大规模数值计算的可靠性和稳定性，以及提升国产处理器性能的有效途径之一。

设计和实现高精度的处理器，可以从硬件和软件2个方面进行。在20世纪60年代到80年代，IBM公司研发出一系列处理器，最大特点是开发出了十六进制的四精度浮点运算硬件逻辑，但是采用的并不是IEEE-754 浮点算术标准，而是IBM独立的标准，其兼容性和推广性有待提高。到了1998年，IBM公司研制的S/390G5处理器[1]正式采用了IEEE-754标准。随后，IBM的z结构处理器得到了硬件支持[2]。软件实现高精度运算主要分为2大类：多部分(Multiple-Component)模式和多数字(Multiple-Digit)模式。多部分模式把一个高精度数据分为若干个标准的浮点数，其数值由这若干个浮点数的数值求和得到。每个浮点数拥有自己独立的指数和尾数。多部分模式数据的精度是工作精度的整数倍，数据之间的运算可以通过浮点操作模拟实现。因此，多部分模式高精度运算具有良好的可移植性，而且可以充分利用高性能处理器所提供的浮点性能，计算速度相对于多数字模式高精度运算有明显提高。本文主要应用多部分模式设计和实现高精度算法库。

自主可控是国家信息化建设的关键环节，是保护信息安全、国防安全的重要目标之一。面向自主可控处理器平台的软件开发是急需解决的问题。Matlab是应用较为广泛的数值分析和图形图像处理商用软件，为广大的科研工作者所熟知和使用。一方面，在某些涉及国家安全的核心科研领域，如核武器模拟、大型航天器设计等，自主可控软件是首要要求；另一方面，Matlab的内部核心代码不公开，在国产自主处理器上的移植也需要授权并由该公司主导开发。考虑到SCILAB是非常接近于Matlab的开源软件，在面向自主可控国产处理器平台上，基于SCILAB进行开发是首要选择。SCILAB是法国国立信息与自动化研究院的科学家开发的开源科学计算软件。此软件的使用、修改和分发不受许可证的限制，自主可控。这样就可以依靠自身研发设计，全面掌握产品核心技术，实现信息系统从硬件到软件的自主研发、生产、升级、维护的全程可控。

基于此，本文利用无误差变换技术，采用double-double数据格式，以SCILAB运算符重载和函数重载为手段，设计和实现面向SCILAB开源软件的多精度的数值算法库。应用本文设计的多精度算法库，科研工作者可以进行更高精度的数值计算和模拟，对数值计算的舍入误差进行有效控制，从而使得计算结果的可靠性和稳定性得到进一步的保障。该算法库主要面向国产自主设计的处理器，具有较好的可移植性，可以方便地将Matlab的数值模拟程序移植到国产处理器平台。本文是文献[3]的扩展版本。

2 多精度算法研究与实现

2.1 无误差变换

2005年，日本学者Ogita和Oishi以及德国学者Rump[4]在前人工作的基础上提出了无误差变换这一概念。设∘∈{+,-,×}，2个浮点数(a,b)∈F且有x=fl(a∘b)∈F，其中F为浮点数集合。在没有上下溢出,舍入模式为就近舍入时，存在：

(a∘b)=x+y

(1)

其中,x表示浮点计算结果，y∈F表示精确的舍入误差结果。将浮点数对(a,b)转化为浮点数对(x,y)，且满足式(1)的过程即为浮点数加、减和乘法运算的无误差变换。

(1)2个浮点数加法的无误差变换[5]如算法1所示。

算法1FastTwoSum

输入：a,b。

输出：x,y。

步骤1x=a⊕b；

步骤2y=b⊖(x⊖a)。

(2)两个浮点数乘法的无误差变换[6]如算法2所示。

算法2TwoProd

输入：a,b。

输出：x,y。

步骤1x=a⊗b；

步骤2[a1,a2]=Split(a)；

步骤3[b1,b2]=Split(b)；

步骤4y=a2⊗b2-(((x-a1⊗b1)-a2⊗b1)-a1⊗b2)。

其中，Split表示把1个浮点数拆成1对浮点数。

2.2 double-double算术

由美国劳伦斯伯克利国家重点实验室的Hida等人[7]开发的软件库 QD(Quotient-Difference algorithm)应用非常广泛，该软件首次提出了双倍双精度(double-double)和四倍双精度(quad-double)格式。日本理化研究院的Nakata[8]开发的软件Mpack针对LAPACK(Linear Algebra PACKag)和BLAS(Basica Liner Algebra Subprograms)实现了高精度的MLAPACK(Multiple precision arithmetic of LAPACK)和MBLAS(Multiple Precision arithmetic of BLAS)，其部分代码是基于QD高精度软件库设计的。2010年，香港科技大学的Lu等人[9]在GPU硬件加速平台上基于QD设计了GQD(GPU QD)高精度函数库。同年，日本筑波大学的Mukunoki等人[10]在GPU上实现了BLAS函数库四倍精度版本。国防科技大学的姜浩等研究人员[11-14]设计实现了多项式求根的高精度补偿数值迭代法。double-double算法设计简单，易于改进当前的数值算法，算法运行较快，适用于本课题的研究。

假定xh和xl是2个浮点数(xh,xl∈F)，x表示xh和xl的没有舍入操作的精确和，即:

x=xh+xl

其中，xh和xl没有交叠，且xh和xl是符合IEEE-754标准的双精度double格式数，那么x就是double-double格式数。

2.3 运算符重载

运算符重载，就是对已有的运算符进行重新定义，赋予其另外一种功能，以满足不同的数据类型。重新定义的运算符重载函数的作用与内置运算符的作用类似，下面重点介绍SCILAB中的重载实现规则。

二元操作数变换规则：

%〈first_operand_type〉_〈op_code〉_〈second_operand_type〉

一元操作数变换规则：

%〈operand_type〉_〈op_code〉

其中，operand_type表示操作数的数据类型,op_code表示操作符(如+，-)的类型。表1和表2列出了部分对应规则。

本文将对表3中所列出的运算符进行重载。

根据运算符重载的规则，以加法重载的实现为

Table 1 Cross reference list to operand_type

Table 2 Cross reference list to op_code

Table 3 Overloading operational character

例，对运算符重载的过程进行展示。把浮点数a，b分割成高位H和低位L，分别记为ah，al，bh，bl，然后实现double-double的加法。在此基础上使用重载命令对加法进行重载。基于double-double数据格式的加法重载过程为：

functionx=add_dd_dd(ah,al,bh,bl)

[s1,s2]=TwoSum(ah,bh);

[t1,t2]=TwoSum(al,bl);

s2=s2+t1;

t1=s1+s2;

s2=s2-(t1-s1);

t2=t2+s2;

[rh,rl]=FastTwoSum(t1,t2);

x=list(rh,rl);

endfunction

deff(′x=%l_a_l(a,b)′,′x=add_dd_dd(a(1),a(2),b(1),b(2))′)

其中，deff表示重载操作。

2.4 函数重载与构建

SCILAB中已经定义了如求绝对值(abs)、求平方根(sqrt)等函数，但是这些函数只适用于普通的浮点数运算。本文将重新定义这些函数，使其适用于双倍浮点数精度的运算。基于double-double数据格式，对表4中的函数实现了重载。

Table 4 Overloading functions

以equal函数为例，本文基于double-double格式对其进行重载，重载具体实现过程为：

functiony=equal_dd(a,b)

y=(a(1)==b(1))&(a(2)==b(2));

endfunction

deff(′y=equal(a,b)′,′y=equal_dd(a,b′));

其中,equal_dd是基于double-double格式重新定义的函数，使用deff进行重载操作。

3 数值实验与分析

本节中，所有的数值实验都是在 IEEE-754 标准[15]双精度下进行的，用在数值实验中的多项式的系数和估值点都是浮点数的形式。精度评估数值实验和时间数值实验的所有程序都是以SCILAB代码撰写的。数值实验的硬件平台是Intel(R) Core(TM) i5-2450M,CPU主频为2.50 GHz，内存为4.00 GB和飞腾处理器FT1500A，主频为1.5 GHz，内存为32 GB；所用的操作系统是UbantuKylin 14.04；开源软件版本为SCILABv 5.5.2。

3.1 幂指数基多项式函数值的高精度可靠试验

多项式的标准格式为：

p(x)=a0+a1x+…+anxn

工程和数学的许多领域需要求多项式在某一点的函数值或导数值，最常用的是Horner算法[16]。Horner 算法能够同时计算多项式函数的任意阶导数，Müller[17]、Olver[18]等学者对Horner 算法进行了深入研究，并给出了数值误差的理论分析。经过研究发现，Horner算法具有较好的稳定性，并且在长时程、大规模甚至是病态的数据运算中，Horner算法都具有比较明显的优势。

Horner算法解多项式的过程如算法3所示。

算法3Horner

输入：p,x。

输出：q0。

步骤1qn=an；

步骤2 fori=n-1:-1:0then

步骤3qi(x) =xqi+1(x)+ai；

步骤4q0=q0(x)。

基于无误差变换，同样写出double-double格式下的Horner算法，即Horner_DD(p,x),如算法4所示。

算法4Horner_DD

输入：p,x。

输出：res。

步骤1x=DD(x)；

步骤2y=DD(0)；

步骤3 fori=n:-1:1then

步骤4y=x*y+a(i);

步骤5res=hi(y)。

实验使用Horner算法对多项式p(x)=(x-2)9进行展开，并计算在其重根x=2附近区域的值。在区间[1.92,2.08]中均匀取样8 000个点，计算得到的结果如图1所示，分别使用double和double-double数据格式计算得出。从图1中可以看到，Horner_DD算法与Horner算法相比，绘出的曲线更加光滑，得到了更好的计算结果。

Figure 1 Horner rules in double and double-double format图1 应用double和double-double数据格式的Horner算法绘制的多项式展开式的图形

经统计，Horner算法的运行时间time_d=0.2160，Horner_DD算法的运行时间time_dd=10.78939，两者运行时间比为time_dd/time_d=34.87。Horner算法共执行2n次浮点运算，Horner_DD算法共执行34n次浮点运算。后者运算量是前者的17倍，计算时间是前者的34.87倍。效率变慢的原因是更多的函数调用和加载。

3.2 Bernstein基多项式函数的高精度可靠实验

计算机辅助几何设计中，单变量多项式一般表示为Bernstein基形式,曲线p(t)的定义为：

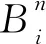
求解曲线p(t)的算法为De Casteljau算法，简称DC算法,如算法5所示。

算法5DC

输入：p,t。

输出：res。

步骤1b(i,1)=b(i),i=1,…,n；

步骤2 forj=1:1:nthen

步骤3fori=0:1:n-jthen

步骤4b(i+1,j+1)=(1-t)*b(i+1,j)+t*b(i+2,j)；

步骤5res=b(1,n+1)。

基于无误差变换，同样写出double-double格式下的DC算法，表示为DC_DD(p,t),如算法6所示。

算法6DC_DD

输入：p,t。

输出：res。

步骤1t=DD(t)；

步骤2b(i)(1)=list(p(i),0),i=1,…,n；

步骤3 forj=1:1:n-1then

步骤4fori=0:1:n-1-jthen

步骤5b(i+1)(j+1)=(1-t)*b(i+1)(j)+t*b(i+2)(j)；

步骤6temp=b(1)(n)；

步骤7res=hi(temp)。

Figure 2 DC rules in double and double-double format图2 应用double和double-double数据格式的DC算法绘制多项式展开式的图形

经统计，DC算法的运行时间time_d=1.460，DC_DD算法的运行时间time_dd=54.76,两者运行时间比为time_dd/time_d=44.73。DC算法的浮点计算量为1.5n2+1.5n+1，DC_DD算法的浮点计算量为33n2+33n+2，后者的运行时间是前者的44.73倍，浮点计算量是前者22倍。效率变慢的原因同样是更多函数加载和调用。

3.3 Chebyshev基多项式函数的高精度可靠实验

Chebyshev多项式是正交多项式的一种，由于其在逼近论中的优异特性而得到广泛应用。计算Chebyshev多项式在某一点的函数值采用迭代的Clenshaw算法[19]。Chebyshev多项式为定义在[-1,1]上的经典正交多项式。使用Chebyshev基对多项式r(x)展开为：

其中，bi为展开系数，Ai(x)为Chebyshev多项式：

A0(x)=1

A1(x)=x

An+1(x)=2xAn(x)-An-1(x)

Clenshaw算法描述如算法7所示。

算法7Clenshaw

输入：r,x。

输出：res。

步骤1an+2=an+1=0；

步骤2 forj=n:-1:1then

步骤3aj=2xaj+1-aj+2+Chebj；

步骤4res=xa1-a2+b0。

基于无误差变换，同样写出double-double格式下的Clenshaw算法，表示为Clenshaw_DD(r,x),如算法8所示。

算法8Clenshaw_DD

输入：r,x。

输出：res。

步骤1x=DD(x)；

步骤2DD(a(i))；

步骤3 forj=n:-1:2then

步骤4a(j)=2*x*a(j+1)-a(j+2)+Cheb(j);

步骤5temp=x*a(2)-a(3)+Cheb(1)；

步骤6res=hi(temp)。

实验计算多项式r(x)=(x-0.75)7(x-1)10的Chebyshev基展开。本文选取一组17项展开的病态数据bi，然后在[0.68,1.15]上取样8 000个均匀点，分别用Clenshaw算法和Clenshaw_DD算法绘出曲线，结果如图3所示。

从图3可以看出，同Clenshaw算法相比，Clenshaw_DD算法给出了较为光滑的曲线，有更好的计算结果。

Figure 3 Clenshaw rules in double and double-double format图3 应用double和double-double数据格式Clenshaw算法绘制多项式展开式的图形

经统计，Clenshaw算法所用平均时间time_d=0.876，Clenshaw_DD算法所用平均时间time_dd=30.28。两者运行平均时间之比time_dd/time_d=43.69。Clenshaw算法的浮点计算量为3n+4，Clenshaw_DD算法的浮点计算量为52n+53。采用double-double格式，在计算量提高14倍的情况下，运行时间增加了43.49倍，造成效率低效的原因是更多的函数加载和调用。

从前面的实验结果可以看到，使用double-double数据格式设计多精度算法库，虽然增加了浮点运算量，但实现了对舍入误差的有效控制，数值计算结果的可靠性得到了保障。

3.4 比较与分析

首先验证3个数值验证实验成果的正确性和有效性。在CPU主频为2.50 GH、内存为4.00 GB、操作系统为Ubuntu Kylin 14.04的Intel处理器上统计CPU的运行时间，得到表5。

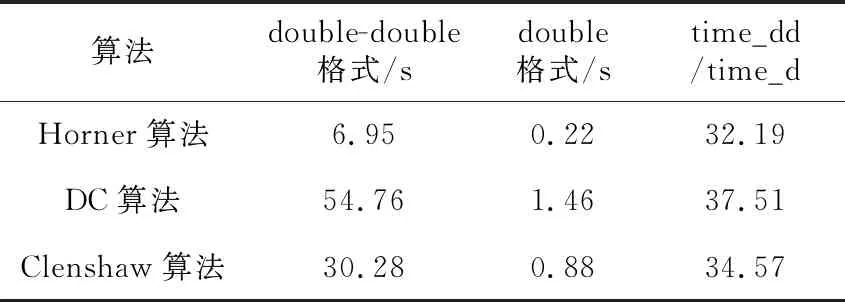
Table 5 Run time of algorithms on Intel processor

从表5可以看出，时间比time_dd/time_d约为30多倍。double-double格式更多地记录了浮点数的舍入误差，计算量更大，调用函数更多，所以花费的时间也比double格式的多。

在Intel处理器上构建好函数库后，将其移植到飞腾处理器平台上，统计CPU运行时间，得到表6。

Table 6 Run time of algorithms on FT processor

从表6可以看出，时间比time_dd/time_d约为30多倍。与在Intel处理器上的结果相近，double-double格式更多地记录了浮点数的舍入误差，计算量更大，调用函数更多，所以花费的时间也比double格式的多。

计算出飞腾处理器上double-double与double时间的比值，与Intel处理器的数据进行比较，得到图4。

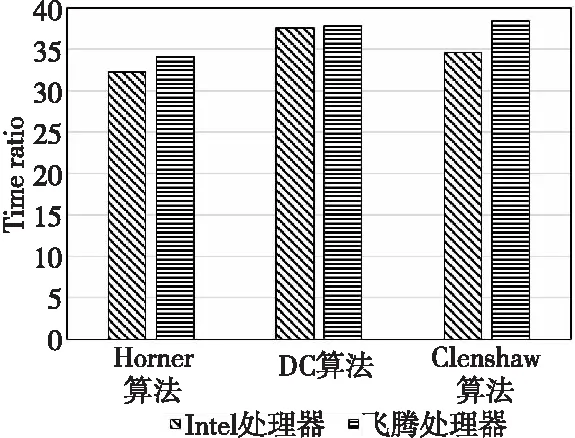
Figure 4 Run time ratio of algorithmsin Intel processor and FT processor图4 算法在Intel处理器和飞腾处理器上运行的时间比time_dd/time_d

2种处理器上，比值time_dd/time_d大致相同，这表明double-double格式下构建的高精度算法库具有较好的可移植性。

4 结束语

随着科学工程计算规模的增加、计算时程的增长，数值结果的精度可靠性越来越受到研究者的重视。对于国防安全等需求，如何在国产处理器上实现自主可控的软件至关重要。本文面向开源软件平台SCILAB，设计了多精度数值算法库。数值实验结果表明，虽然多精度算法增加了一定的浮点运算量，但计算结果的可靠性得到了进一步的保证，有效控制了计算机舍入误差的累积。与此同时，通过对国产自主可控处理器上的结果和Intel处理器上的结果对比，表明本文设计的多精度算法库具有较好的可移植性。本文的工作可以用于提升大规模科学工程计算的稳定性和可靠性，以及为在国产自主可控处理器上实现自主可控软件提供了支持。未来准备在前期工作的基础上，继续丰富该算法库的功能，为应用提供更多支持。