基于改进遗传算法的连锁便利店配送路径优化 *
李丹莲,曹 倩,徐 菲
(北京工商大学电商与物流学院,北京 100048)
1 引言
便利店的兴起缘于超市的大型化与郊外化,是一种能满足人们需求的便利小超市[1]。学者将便利店描述为面积100平方左右,主要经营非个性化商品,营业时间长,多为连锁方式存在[2,3]的商店。连锁便利店经营食品、生活用具等,其中食品还包括了保质期短的生鲜水果、便当、酸奶等,此外,商店的规模很小,因此有必要实施有效且低成本的补货策略[4]。在实地调查后发现,现北京市的大多数连锁便利店(连锁水果店和一般连锁店)都为每日补货一次[5,6]。学者们对7-11便利店的研究表明,连锁便利店是基于市场支配战略进行扩张,体现形式是在重点区域内集中开店,利用快速密集的布局达到规模效益[7,8]。其配送特点为:(1)时间窗口较为集中且十分密集[9,10];(2)具有一个配送中心[11];(3)各便利店需求量不同[12];(4)成本构成多样性[13]。以上几点决定了这种情况下的连锁便利店的物流供货问题属于单车场多车型带密集半软时间窗问题SHVRPDSTW(Single depot Heterogeneous fleet Vehicle Routing Problem with Dense Semi-soft Time Windows)。为了求解此问题, 本文提出了多染色体遗传算法。
2 SHVRPDSTW数学模型构建
传统的连锁便利店的物流配送是由单车型和单配送中心组成,但每个分店(客户点)的需求量是不同的,单车型在实际场景中并不灵活,多车型在物流配送中的应用会越来越广泛。因此,为了车辆调度的灵活性,SHVRPDSTW模型假设配送车队由多种车型组成。并且,每个分店(客户点)都具有半软时间窗,晚于时间窗口到达的车辆需支付晚到惩罚成本,早于时间窗口到达的车辆需等待至时间窗起始时间。SHVRPDSTW可视为VRP(Vehicle Routing Problem)问题的分支,假设已知各客户点的需求量以及配送路径序列和车辆序列,建立数学模型,其约束如下所示:
(1)只有一个配送中心,其具有多种车型的配送车辆。
(2)每种车型具有不同的额定载重量、固定成本和行驶成本。
(3)车辆驾驶员的工资将计入车辆的固定成本。
(4)所有车辆从配送中心出发并最终返回配送中心。
(5)待配送客户点有各自的需求量、时间窗和卸货服务时间。
(6)配送车辆应在客户规定的时间窗内到达客户点,若在时间窗后到达,需支付超时惩罚成本;若在时间窗前到达,需等待至客户点的时间窗起始时间。
(7)所有车辆不可超载。
(8)一辆配送车辆可以服务多个客户点,每个客户点只能被一辆车服务一次。
(9)所有配送车辆均匀速行驶。
2.1 符号表示
设V为配送点集合,其中0为配送中心,V={0}∪D={0,1,2,…,n};D为n个客户点集合;设M为车型集合,M={0,1,…,h},共计h+1类。模型的相关变量和参数表示如下:
β:迟到惩罚成本;
Cm:车型m的额定载重量,m∈M;
Km:车型m可用数量,m∈M;
ρm:车型m固定成本,m∈M;
εm:车型m运输单位距离成本,m∈M;
ti,j:从点i行驶到点j的行驶时间,i∈V,j∈D;
di,j:从点i行驶到点j的行驶距离,i∈V,j∈D;
ci,j:从点i到点j的配送成本,i∈V,j∈D;
gi:客户点i的需求量,i∈D;
ai:客户点i的服务时间,i∈D;
wi:客户点i开始服务时刻,i∈D;
[ei,li]:表示客户点i的服务时间窗;
2.2 模型公式
本文优化目标为总配送成本Z最小化,包括配送距离成本、惩罚成本和固定成本,可描述为式(1)所示:
(1)
(2)
wj=wi+max(ei-wi,0)+ai+ti,j,
w0=0,i≠j,i,j∈V
(3)
(4)
(5)
(6)
(7)
(8)
式(2)代表了目标函数中的配送成本计算方法;式(3)表示客户点j的开始服务时间wj的更新方法;约束(4)表示配送中心每种类型的车辆的使用数量不应超过此类型车辆的可用数量;约束式(5)表示所有车辆均从配送中心出发并且返回配送中心;约束式(6)表示每个客户点只被服务一次;约束式(7)表示车辆在服务客户点i后,到达下一客户点或回到配送中心;约束式(8)表示每条路线的总需求量不高于此路线的配送车辆容量。
3 多染色体遗传算法设计
传统的遗传算法求解单车场单车型车辆路径问题效果较好,但是求解SHVRPDSTW时,由于同时考虑“多车型”和“时间窗”2个约束,解的质量将受到影响,甚至存在无解的情况。以下设计参考陈呈频等[14]对于多车场多染色体遗传算法的研究,并在此基础上加入“时间窗”约束,每个个体被设定包含2条染色体——配送路径序列与车辆序列,表示所有可调用的车辆和其配送路线,有效避免无效解甚至非法解的产生[14]。
3.1 染色体的编码与初始化
每辆车的配送路线只有一条,并且每个客户点每次只能被一辆车服务。将客户点和车辆进行编码:
(9)
式(9)表示各车型数量总和,车辆序列染色体顺序编码为:Seqv={1,2,3,…,Vehiclesum}。配送路径序列染色体顺序编码为:Seqc={0,1,2,3,…,n},共计n个客户点,0代表配送中心。
编码完成后,配送路径序列染色体随机初始化,然后与其对应的车辆序列染色体随机初始化,如图1所示。车辆序列染色体代表可使用的车辆及其使用顺序;配送路径序列染色体代表待配送的客户点的服务顺序。

Figure 1 Chromosome initialization图1 染色体初始化
3.2 任务分配与适应度计算
个体的适应度决定了个体的优劣性,决定一个个体在迭代过程中是否可以被保留。根据个体的配送路径序列染色体与车辆序列染色体,安排配送任务并求出适应度,流程如下所示:
(1)对于种群中第i个个体,按照其车辆序列染色体选择一辆可用的车辆,再在其配送路径序列染色体中顺序选择尽可能多的待配送的客户点,客户点总需求量不应超过该车辆的额定载重量。
(2)判断配送路径序列染色体中的所有客户点是否已被配送,若存在待配送的客户点,则返回(1),若无则转至(3)。
(3)完成任务分配后,生成种群中第i个个体的配送方案Ji,根据式(1)计算其总成本Zi。
(4)取第i个个体对应的成本Zi,令fi=1/Zi,fi即为第i个个体的适应度。
例:设种群中第t个个体的配送路径序列染色体为[4,5,6,3,1,2],其对应的客户点需求量为[300,200,200,400,100,300];车辆序列染色体为[2,3,1,4,5],其对应的车型为[1,2,2,3,3],车型对应的额定载重量为[300,500,500,400,400];根据上述任务分配方式则可知分配的任务为:
①安排序号为2车型为1的车辆,服务路线为:0-4-0;
②安排序号为3车型为2的车辆,服务路线为:0-5-6-0;
③安排序号为1车型为2的车辆,服务路线为:0-3-1-0;
④安排序号为4车型为3的车辆,服务路线为:0-2-0;
⑤其他车辆不分配配送任务。
之后根据此分配的任务结合式(1)求出总成本Zt和适应度ft=1/Zt。
3.3 选择、交叉、变异、逆转操作
在本文算法中,种群内每个个体包含2条染色体——配送路径序列染色体和车辆序列染色体。染色体的交叉方法为部分映射交叉方法PMX(Partially Mapped Crossover)[15],如图2所示。
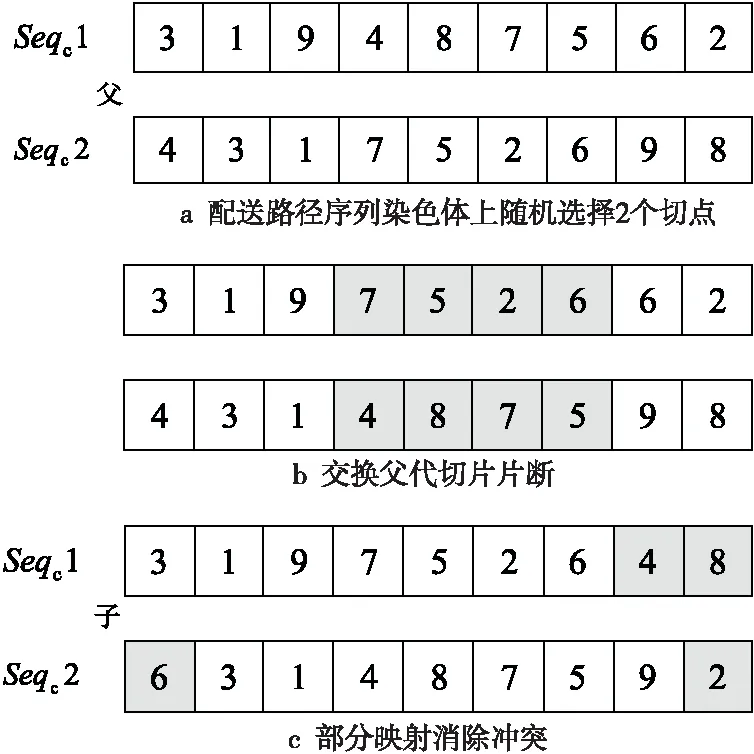
Figure 2 Chromosome crossing图2 染色体交叉
根据变异概率分别变异配送路径序列染色体和车辆序列染色体。方法是在个体的染色体中使用2-opt算法进行变异操作[16],如图3所示。
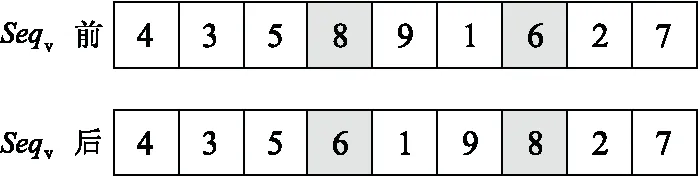
Figure 3 Chromosome mutation图3 染色体变异
逆转操作是随机选取染色体中的2个位点,颠倒两位点间的基因序列前后顺序,并且根据逆转后的个体的适应度决定是否保留逆转结果。若其适应度增大则保留逆转结果,反之撤销该操作。如图4所示。

Figure 4 Chromosome reversion图4 染色体逆转操作
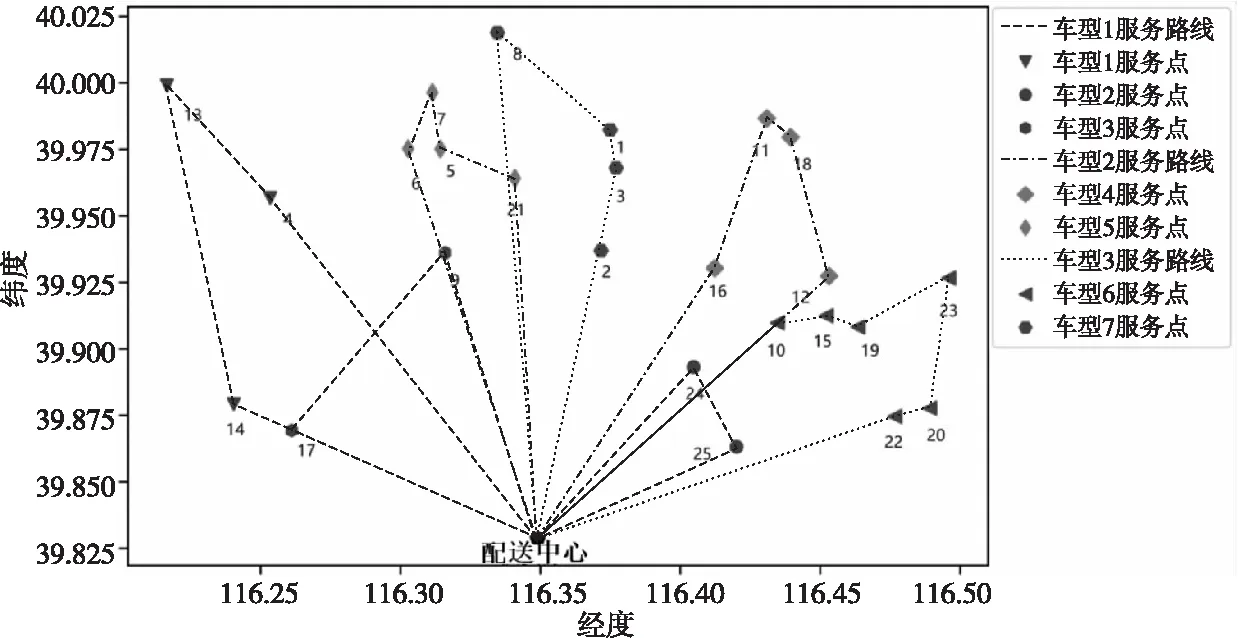
种群规模为S,选择操作通过轮盘赌规则和代沟选择参数PGap(0 步骤1设置本文算法的参数:交叉概率Pc、变异概率Pm、种群规模S和遗传迭代轮数R。 步骤2初始化种群:种群中的个体包含的配送路径序列染色体和车辆序列染色体。 步骤3选择操作:根据适应度和代沟选择参数PGap,选择S×PGap个个体继续交叉、变异、逆转操作后进入子代种群,其余S×(1-PGap)个未被选择的个体直接保留至子代种群。 步骤4交叉操作:根据交叉概率Pc对被选择个体的配送路径序列染色体和车辆序列染色体,分别通过PMX方法进行交叉操作生成交叉后的新个体。 步骤5变异操作:根据变异概率Pm对步骤4生成的新个体,通过2-opt算法变异生成变异后的新个体。 步骤6逆转操作:对每个个体的2条染色体分别进行逆转操作,并根据逆转后适应度大小决定是否保留逆转结果。 步骤7子代种群的生成:经过步骤4~步骤6操作后生成的S×PGap个个体,与选择操作中的S×(1-PGap)个个体组成子代种群。 步骤8对种群重复步骤3~步骤7的操作,直到达到规定迭代轮数R,若达到规定的迭代轮数R,输出最后一代种群中适应度最高的个体、总成本和其对应的配送任务作为最终结果。 本文实验中的连锁便利店的配送中心和25个客户点均位于北京市城区,间接模拟真实配送路径业务场景,通过导航类程序测量客户点与供货中心间运输时间和距离,并在Matlab R2016a上与传统遗传算法进行对比实验,用于验证所提出的多染色体遗传算法对SHVRPDSTW的有效性和可行性。实验的运行环境为Intel Core i5-7200 HQ 2.5 GHz CPU,8 GB内存,Windows 10操作系统。 实验中车辆分1,2,3类车型共计13辆车,分别对应的可用辆数为5,4,4;容量(千克)为600,800,1 000;单位距离运输成本(元)为5,7,8;固定费用(元)为30,40,60。车辆匀速行驶速度(km/h)为40,晚到惩罚(元/分钟)为5。配送点详细信息如表1所示。 Table 1 Distribution node set 表1 配送点集合 本文算法使用多染色体进行遗传优化,为了验证其有效性,将其结果与传统的单染色体(单序列)的遗传算法的测试结果进行对比。参考熊浩等[18]的算法设计,构建了仅包含配送路径序列染色体的并没有逆转操作的单染色体遗传算法。在同样实验条件和算例中,各算法分别测试10次:迭代轮数R=1000,种群大小S=100,交叉概率Pc=0.8,变异概率Pm=0.2。 算法运行结果如表2所示,在密集半软时间窗约束下传统遗传算法的平均总成本为2 434.91元,而改进遗传算法求解得到的平均总成本为2 258.83元,改进后平均总成本节约了7.25%。同时也明显降低了最低和最高总成本约7.23%,9.35%。结果表明,多染色体遗传算法能有效提高求解质量。 Table 2 Comparison of the results of two algorithms 实验的平均进化曲线如图5所示,改进后的多染色体的遗传算法与传统的单染色体的遗传算法相比,收敛速度快,且得到的最优成本低,能够有效地防止算法陷入局部最优解。由此可得,将车辆序列作为第2条染色体参与遗传的算法,在求解SHVRPDSTW时,具有更快的收敛速度和更强的全局搜索能力。 Figure 5 Average evolution curves of two algorithms图5 2种算法平均进化曲线 如图6所示,客户点配送总共使用7辆车,车型分别为2,2,2,3,2,1,1,与传统遗传算法相比,改进遗传算法节约了一辆车的购置成本。利用多染色体遗传算法求解算例的最优配送路径为:0→4→13→14→0→22→20→23→19→15→10→0→24→25→0→16→11→18→12→0→17→9→0→2→3→1→8→0→6→7→5→21→0。例如序列为1型号为1的车辆,配送路径为0→4→13→14→0,表示其从配送中心出发沿经客户点4,13,14配送货物,完成任务后返回配送中心。 Figure 6 Delivery route optimization graph based on improved multi-chromosome genetic algorithm图6 改进多染色体遗传算法下最优路径规划图 本文中建立的SHVRPDSTW数学模型,属于具有单一配送中心、供货时间较为密集、车型选择多样的物流供货场景,可运用于连锁便利店、小型超市、农产品超市、中央厨房等的车辆配送路径规划中。针对SHVRPDSTW的复杂性,提出了改进多染色体遗传算法——建立了车辆序列与配送路径序列2条染色体。然后与传统单染色体遗传算法在Matlab R2016a上实验比较,结果表明,多染色体遗传算法的配送总成本明显减少,可求出全局最优解,明显提升了解的质量,验证了改进算法的有效性。最后利用改进遗传算法对SHVRPDSTW场景进行算例求解,得到优化后的配送路径规划,为类似问题提供了可行方案。因此,本文提出的多染色体遗传算法,可填补在时间窗约束下单一车场多车型密集半软时间窗车辆路径规划问题空缺,具有一定现实意义。3.4 算法的整体流程
4 实验分析
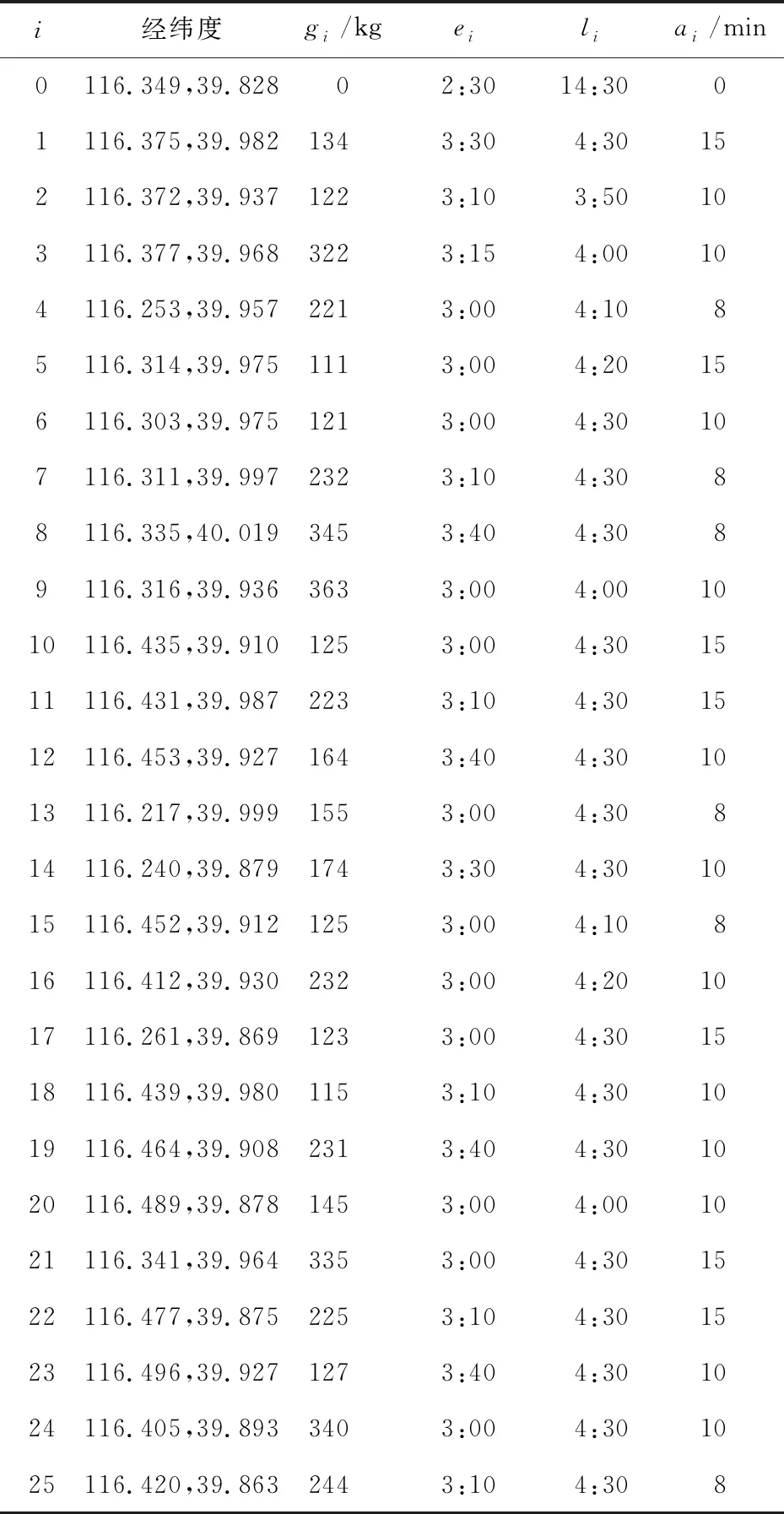
4.1 算例设计
4.2 实验结果及分析
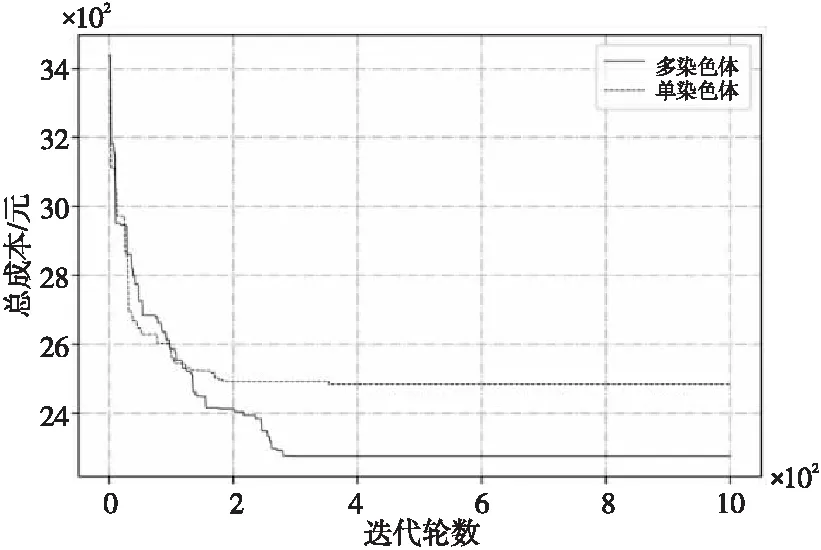
4.3 算法实现效果与可视化

5 结束语

