机制砂高强混凝土强度和弹性模量试验研究

刘晓龙

（中铁十六局集团第一工程有限公司， 北京 101300）

0 引言

随着我国建设事业的迅速发展，基于混凝土设计的主要趋势，越来越多的大型土木工程项目要求河砂作为普通细集料。河沙枯竭可能发生在许多地方，特别是远离任何河流的地方。在这种情况下，使用机制砂可能是一个简单可行的选择。与河砂相比，机制砂具有一些优点，如可以存在聚晶微粉(AMF)。关于 AMF 在机制砂混凝土(MSC)性能方面的作用，有相互矛盾的报道。一些研究人员报告了在 MSC 中随着 AMF 含量的增加，坍落度减少和需水量增加。另一些文献认为，对于 MSC 的性能而言，AMF 存在一个最佳含量，AMF 的存在可能有助于获得更高的抗压强度。据报道，抗压强度受到许多不同因素的影响，这可能导致不同的报道结果。研究发现，AMF 对水泥浆体流变性能的影响受到表面性质、粒径和矿物类型的影响。

1 机制砂混凝土性质概述

机制砂是用碎石或碎石经机械破碎分离而成的粒径小于5mm 的人造砂，近年来已成为河道防护用天然砂的替代品。与天然砂相比，机制砂具有表面粗糙、棱角多、石粉含量大等特点。在传统的生产工艺中，碎石或砾石直接放入破碎机中，粒度小于75 μm 的石粉易与泥块或风化层中形成的泥粉混合。因此，对于机制砂中石粉对混凝土性能的影响有不同的看法。为了避免石粉的不利影响，现行《建筑用砂标准》(GB/T14684-2001)对 C30-C60级浇注混凝土的机制砂石粉含量相对严格的限值低于5.0% ，极大地限制了机制砂在结构混凝土中的应用。

2 机制砂混凝土试验探究方法概述

机制砂由机械按照一定的破碎和筛分工序用碎石制成，具有不同于天然砂的许多特性，如不规则多边形颗粒尖锐、表面粗糙新颖、充满石粉等，使混凝土在新鲜和硬化状态下具有不同的性能。因此，近年来我国对机制砂混凝土进行了大量的研究。作为结构设计的基础，在混凝土与机制砂混合时，应清楚地了解混凝土的基本性能，包括抗压强度、抗拉强度、断裂模数和弹性模量之间的关系。然而，以往对机制砂混凝土的研究很少涉及这一方面。关于这些属性的部分测试数据在已发布的参考文献中被分离。在这种情况下，我国现行的混凝土结构设计规范没有对机制砂混凝土与普通天然砂混凝土进行区分，也没有对其适应性进行综合评价。本文在总结已发表文献的试验数据的基础上，通过统计分析，探讨了机制砂混凝土的上述性能之间的关系，并与普通混凝土进行了比较。对机制砂混凝土这些性能的设计应用提出了一些建议。

然而，为了确保石粉的极限含量，尽可能地消除粉末泥浆，传统的机制砂方法往往将水洗作为最终的测定方法。由此产生了两个问题: 一是机制砂中大量石粉被冲刷出来排入河道造成的二次环境污染，二是混凝土综合利用中自然资源的浪费。针对这一情况，提出了将传统的水洗工艺改为第一步工艺的技术改进方案，使石材在破碎前进行清洗，避免将泥浆混入原料中，最后保留完整的石材粉末。与传统的机制砂不同，全石粉砂被称为原机制砂。原机制砂中石粉的含量一般都超过规定的限量。

3 机制砂混凝土强度和弹性模量试验

3.1 机制砂混凝土轴向压缩强度与立方压缩强度的理论关系研究

首先本文从已有的文献中收集了55 组试验数据，混凝土的立方抗压强度范围为28.8 MPa 至102.5 MPa。通过统计分析，轴向压缩强度与立方体压缩强度之间的关系符合0.947 的关系系数和0.081 的标准差，GB50010 中规定的普通混凝土的关系式和机制砂的试验结果进行对比能够得出，普通混凝土的试验结果在混凝土立方抗压强度测试值小于60MPa 时接近试验值的下限，而混凝土立方抗压强度大于60MPa 时接近于标准中提出的公式关系。因此，GB50010 中规定的普通混凝土的关系式可用于结构设计机制砂预测混凝土的轴向抗压强度。在已有试验研究的基础上，原机制砂性能和石粉掺量对新拌混凝土工作性能和硬化混凝土性能有不同的影响。为此，进行了原机制砂、石粉固有特性的系列试验，研究了石粉含量对砂性能和水泥砂浆强度的影响，并介绍了主要试验结果。

3.2 原机制砂石粉含量对强度发展的影响试验探究

在实验的过程中选择具有合格稳定性的42.5 级普通硅酸盐水泥和具有已知的物理力学性能的原机制砂进行试验。对原机制砂进行分选和测定后，重新调整了具有砂质的石粉含量。5 毫米-10 毫米和10 毫米-25 毫米系列的石灰石粉按1:1 的比例混合，并且对其物理和机械性能进行检测和记录。在混凝土配比的控制方面将混凝土的设计等级为 C50，只需改变石粉含量分别为3% 、7% 和13% ，减水剂含量为水泥质量的0.75% 。试验方法符合《普通混凝土力学性能试验方法标准》(GB/T50081-2002)的规定。对150mm 的立方体进行了3 d、4 d、7 d、14 d、28 d、56 d、90 d、120 d、150 d 和180 d 的立方体抗压强度测试，共测试了27 个周期。

首先对砂砾的特征进行研究和分析，图1 示出了天然砂和原机制砂的图片，可以看出天然砂呈淡黄色，颗粒较大的圆形平原表面，粉砂含量较高，原机制砂呈凹凸灰色，颗粒呈不规则多边形颗粒状，表面粗糙，边缘尖锐，石粉含量较高。粒度特征通常用点状、长宽比和丰满度三个指标来描述。指向性反映了籽粒边缘和角点的相对敏锐度，长宽比用于评价籽粒是否呈针状，丰满度是与籽粒表面光滑程度有关的籽粒凸度的度量。与天然砂相比，原机制砂的点状和长宽比较大，含有更多的针状颗粒。然而，天然砂由于长期磨损而表面光滑，所以充满率较大。

图1 天然砂(左)和原机制砂(右)的外观示意图

原机制砂的颗粒特性一般会导致颗粒之间产生较大的机械啮合力，有利于砂与水泥的粘结，但不利于新拌混凝土的流动性，在拌制混凝土时应予以注意。

之后对于砂砾的级配进行统计和分析，根据颗粒组成的统计分析，天然砂属于 II 级配上下限中间具有理想级配曲线的中型砂，原机制砂属于末端过粗级配、中间极少级配的粗砂，颗粒大于2.36 mm 或小于0.15 mm，但小于0.6 mm ー1.18 mm，符合 I 级配砂的技术要求。砂的级配对于控制新拌混凝土的含水量具有重要意义。4.75 mm 至0.15 mm 的颗粒效果更好，特别是4.75 mm 至2.36 mm 的颗粒效果更好。因此，应采取相应的措施来满足新拌混凝土的工作性能。

在此基础上对机制砂的细度分布进行分析和研究，图2 示出原机制砂中石粉的细度分布和各粒度级的合格率。原石粉的平均粒径为29.99 μm，小于75 μm 的颗粒含量为90.2% ，小于10 μm 的颗粒含量为24.6% ，小于10 μm 的颗粒含量为25.5% ，小于30 μm 的颗粒含量为40.2% 。由于水泥浆体系中石粉微细颗粒的填充作用以及集料孔隙等因素的影响，石粉细度呈均匀连续分布，有助于提高混凝土的密实度。根据相关研究，石粉的微细晶粒，尤其是小于10μm 的微细晶粒，有促进水泥水化的晶核效应。

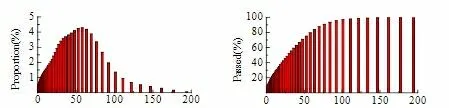
图2 细度分布(左)及各粒度级石粉的通过率

通过试验能够得出不同石粉含量、不同时间的混凝土抗压强度的发展情况。石粉含量对砂性能的影响从图3 可以看出，在0.15ー2.36 mm 的水平范围内，石粉含量对筛子累积剩余量(ATR)的影响为负相关，相关系数大于0.99。根据试验数据，可将分级范围划分为0.6 mm 水平筛余物的累计剩余量。当石粉含量低于6% 时，砂的级配属于 I 级。当含量在6% ー14% 之间时，属于范围 II。当含量在14% ー20% 之间时，属于范围 III。

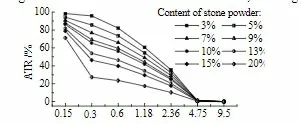
图3 石粉含量对砂级配的影响示意图

综合来看，原机制砂的石粉含量在试验范围内是合适的。通过试验研究了原机制砂、石粉的性能，以及石粉掺量对砂性能和水泥砂浆强度的影响。研究结果有助于解释原机制砂在不同石粉掺量下混凝土的一些特性。与普通混凝土相比，混凝土的增量更为理想。并且根据得到的混凝土配比对机制砂强度的影响机制关系能够对混凝土的强度进行有效准确的预测，原机制砂中的石粉对混凝土强度的影响与普通机制砂中掺入石粉的混凝土强度的影响差别很大，原机制砂中石粉含量低于5% 的极限值不适合用于 C50 级混凝土。

3.3 石粉掺杂量对机制砂的弹性模量的影响试验探究

在进行石灰石弹性模量检测的过程中利用高掺量石粉制备高强高性能混凝土，以扩大石灰石粉碎废料的应用范围，实现石灰石粉碎废料的利用。采用52.5 级普通硅酸盐水泥，3 天抗压强度为30.3 MPa，28 天为62.4 MPa。矿物掺合料为I 级粉煤灰(FA)和磨细高炉矿渣（GFBS）。粗集料为5ー25mm 连续级配的石灰石碎料。采用两种不同的砂作为细集料。第一种是细度模数为3.4 的石灰石砂，原始粉尘含量(＜ 75μm)为3.5% 。用河砂与质谱进行比较，其细度模数为2.7。采用湿筛法从剩余石灰石砂中分离出目数小于75μm 的石灰石粉尘。采用105 ° c 干燥24h，研磨至75μm 的方法制备粘土粉。掺合料为 JG-2 高效减水剂和 JG-3 缓凝超级塑化剂，按重量1:1 混合。

人们普遍认为，混凝土的弹性模量取决于其抗压强度、体积密度、骨料的相对体积和刚度(刚度与骨料来源密切相关)。本文的结果表明，MS 混凝土与 RS 混凝土的弹性模量没有明显差别，微细粒含量最高的 MS 混凝土的弹性模量为14% ，而 MS 混凝土的弹性模量随微细粒含量的增加而降低。微细粉含量的增加，一方面改善了混凝土的抗压强度，使弹性模量趋于增加，但另一方面增加了浆体体积，然后降低了混凝土的弹性模量。用 FA 或 GBFS 替代水泥后，材料的弹性模量降低。

4 结束语

综上所述，机制砂具有不规则多边形颗粒尖边、表面粗糙、石粉含量大等特点，对混凝土的性能影响不大。作为混凝土结构设计的基础，必须清楚地了解混凝土的基本力学性能，如抗压强度、抗拉强度、断裂模数和弹性模量之间的关系。本文总结了已发表文献中的试验数据，并通过与普通混凝土的统计分析比较，讨论了这些性能之间的关系。结果表明，按照我国现行规范中规定的普通混凝土的抗拉强度计算公式，可以预测混凝土的轴压抗压强度和抗拉强度，但当混凝土强度等级低于 C30 时，预测抗拉强度应乘以减小系数。机制砂混凝土的弹性模量大于普通混凝土的弹性模量，本文应用公式进行展望。同时，提出了断裂模数的计算公式。