球形燃料孔隙内汽泡生长与脱离

张晓杰，白博峰

(1.华龙国际核电技术有限公司，北京 100036；2.西安交通大学动力工程多相流国家重点实验室，陕西 西安 710049)

球形燃料核反应堆因安全性高、燃料利用率高、体积小、经济性等优点，具有广阔的发展前景。反应堆中球形燃料构成的多孔结构内的沸腾核化过程——汽泡的生长、脱离及运动等问题是对球床核反应堆进行研究的基础，同时燃料间隙内的沸腾对核反应堆的运行效率、运行安全等都有很大的影响。

对于加热面上的汽泡生长，主要有两种观点，一种观点认为汽泡生长是汽泡周围所有界面蒸发的结果，蒸发所需的热量由汽泡周围的过热流体层提供。进一步研究表明，供给汽泡长大的热量不仅来自过热液体层(壁面间接供热)，而且来自与汽泡根部直接接触的加热壁面(壁面直接供热)[1]。另外一种比较普遍的观点认为在汽泡底部形成一层微液膜，液膜吸热蒸发促进汽泡生长[2]。当使汽泡附着在表面的作用小于促使其上升的作用时，汽泡便脱离加热表面，脱离半径受流体和蒸汽的惯性、流体对汽泡的阻力、汽泡所受浮力、表面张力等作用之间平衡关系的影响。不少学者在考虑多种影响汽泡的作用的基础上，对汽泡脱离半径提出了若干经验或理论分析表达式，然而这些表达式并不能取得一致。

由于结构的复杂性，球形燃料多孔结构内的汽泡生长、脱离、运动及传热都与大空间内不同。Chu[3]通过实验观察得到了大直径(≥6 mm)球形颗粒堆积的多孔结构内的气泡运动特点，并将其模型化，根据浮力与表面张力的平衡得到泡状流气泡直径表达式。Jamialahmadi[4]对球形颗粒堆积的多孔结构进行可视化实验，低气速下，小气泡不需明显的变形和合并就可通过球床，气泡的直径主要与孔隙大小、表面张力及浮力有关，并根据实验结果给出了气泡直径表达式。张晓杰等[5]通过实验，得到了常压底部加热条件下直径4 mm、6 mm、8 mm玻璃球构建的多孔结构内池沸腾沸腾汽泡的生长及脱离过程。Wang[6]根据实验现象及表面张力与浮力平衡提出了汽泡生长模型，通过计算得到了汽泡脱离时的几何形状随颗粒直径的变化。

1 多孔结构内的汽泡生长和脱离分类

根据球形颗粒堆积多孔结构内的流动沸腾可视化试验，可以把汽泡生长脱离分为两类。第一类，汽泡长到一定体积后作为一个整体向上滑移，如图1所示。第二类，汽泡在生长过程中由于流道结构影响，在孔隙处形成一个较细的颈部，汽泡体积足够大时，便从该颈部断裂，脱离孔隙内部汽泡，向上运动，如图2所示。

图1 汽泡滑移Fig.1 Bubble sliding

图2 汽泡脱离Fig.2 Bubble departure

2 汽泡滑移模型

根据汽泡动力学基本原理，结合多孔结构内流动沸腾可视化试验结果，可构建球形燃料颗粒堆积的多孔结构内的汽泡滑移模型。四个球体构成图3所示的正四面体结构，该结构为汽泡在多孔结构中生长的基本孔隙之一。一定的壁面过热度下，在两球体接触点附近的角缝区域形成汽泡，并缓慢变大，占据正四面体结构中心孔隙。汽泡充满孔隙后，便向孔隙外部区域扩展，如图4所示。假设汽泡在侧面三个方向以及底部方向的生长变形量是相等的，可建立图4、图5所示的汽泡模型。汽泡界面分为两部分，一部分是与球体接触的凹面，另外一部分是与液体接触的凸面。汽泡凸面随着热流密度增大向外扩张，曲率半径r增大，凹面面积相应增加，汽泡体积变大。图5中Rp为燃料球半径，r为汽泡曲率半径。

图3 基本球形燃料孔隙之一Fig.3 The basic pore Structure

图4 球形燃料孔隙的汽泡Fig.4 The bubble in porous media composed of spherical fuel elements

图5 汽泡模型Fig.5 Bubble Module

2.1 受力分析

沸腾汽泡在多孔结构内受浮力、表面张力、接触力、升力、不稳定生长力、拖曳力和惯性力等作用。汽泡受到的合力∑F≥0时，开始向上滑移，如图1所示。∑F=0时汽泡处于临界状态。

∑F=FB+FS+Fcp+FL+Fdu+Fqs+Fbi

(1)

2.1.1 浮力

汽泡受到的浮力为，

FB=(ρL-ρV)gVb

(2)

式中:

(3)

(4)

(5)

(6)

(7)

2.1.2 表面张力

汽泡受到的表面张力为汽泡与上部颗粒接触所受的表面张力及与侧面颗粒接触的表面张力之和，即:

FS=-σLcosα-3σLcosαsinβ

(8)

式中:β——侧面与中心线的夹角。

即图5中侧面1与中心线的夹角:

(9)

(10)

(11)

2.1.3 接触力

接触力是由于汽泡直接与固体接触，汽泡与固体壁面接触处内外压力不同而受到的力，可表示为[7]:

(12)

2.1.4 升力

汽泡或颗粒在剪切流场中运动时，会受到垂直于相对运动方向的升力作用。类似于Kolev升力模型[8]，汽泡的升力可表示为:

(13)

式中:ud——汽泡上升速度，近似为2drb/dt。

因此，升力FL可以表示为:

(14)

2.1.5 不稳定生长力

不稳定生长力是由于汽泡生长不均匀而引起的，其表达式为[9]:

(15)

2.1.6 拖曳力

把汽泡简化为球形，则受到的拖曳力为:

(16)

式中:CD——拖曳力系数[10];

(17)

2.1.7 惯性力

汽泡惯性力表达式为:

(18)

式中:

(19)

(20)

则，汽泡惯性力可表示为:

(21)

2.2 传热分析

假设汽泡生长前壁面附近的过热液体层的温度均匀，且等于壁面温度TW。汽泡开始生长后，过热液体层中将发生瞬态导热现象。忽略汽泡周围液体的运动，近似地将汽泡周围的热边界层当作一维半无限大平板，x轴以汽液分界面为起点，由导热微分方程可以得到汽液分界面的温度梯度为:

(22)

根据Han和Griffith的汽泡生长模型[53]，汽泡生长过程的热平衡方程为：

Qg=QL,V+QW,V

(23)

式中：Qg——供汽泡生长的热量；

QL,V、QW,V——通过过热液体层、壁面传递给汽泡的热量，即：

(24)

则，汽泡的生长速率可表示为：

(25)

式中：φc——过热液体层的形状因子；

(26)

汽泡生长速率表达式中涉及时间变量，形式复杂，同时该表达式还涉及汽泡生长的等待时间，在计算过程中处理起来极其复杂。为了简化，在计算过程中假设汽泡生长呈线性[10]，汽泡生长速度按下式计算：

(27)

式中：Ctg=0.029 6。

与汽泡生长速率有关的力包括汽泡生长力Fdu和汽泡惯性力Fbi，相对于汽泡受到的浮力FB、表面张力FS等Fdu和Fbi较小，故此简化对汽泡所受合力影响不大，可以采用。

2.3 汽泡滑移临界曲率半径的影响因素

2.3.1 颗粒半径

不同颗粒半径下，汽泡体积、汽泡与颗粒的接触面积不同，汽泡受力发生变化，所以汽泡开始滑移的临界曲率半径随颗粒大小变化。以纯水为工质进行计算。图6为液体流速为0.02 m/s不同压力下汽泡临界曲率半径(rcr/Rp)随颗粒半径(RP)的变化，rcr/Rp随RP的增大而减小。颗粒半径增加，孔隙增大，汽泡体积增大，汽泡受到的浮力、表面张力等增加，而浮力的增加速度大于表面张力等其他力，故rcr/Rp随着颗粒的增加而减小。在颗粒半径较小时，rcr/Rp的变化速率缓慢，随着颗粒半径的增加，其变化速率逐渐增大。

图6 不同压力下rcr/RP随RP的变化Fig.6 Curve ofrcr/RP under different fluid pressure

2.3.2 压力

不同压力下，汽泡临界曲率半径有一定差异。如图6所示，颗粒半径相同时，压力越高，rcr/RP越小；颗粒半径越大，压力对汽泡临界曲率的影响越大。压力升高，液体密度降低，浮力减小，同时表面张力系数降低，表面张力减小，但是表面张力系数的变化率大于密度的变化率，故随着压力升高表面张力比浮力降低的更多，汽泡体积较小时就能达到受力平衡。

2.3.3 液体流速

液体流速不同，流体对汽泡的拖曳力不同，故液体流速对汽泡临界曲率半径也有一定的影响。图7为压力0.1 MPa，液体流速分别为0.01 m/s和0.05 m/s时的Rp-rcr/Rp曲线，压力和颗粒半径相同时，流速越高，汽泡临界半径(rcr)越小。流速增大，汽泡受到的拖曳力便增加，从而导致汽泡临界半径减小。

图7 不同流速下rcr/RP随RP的变化Fig.7 Curve of rcr/RP under different fluid velocity

3 汽泡脱离

3.1 物理模型及受力分析

部分汽泡在孔隙内长大并从颈部断裂后脱离，进入上部孔隙，由此建立图8、图9所示的汽泡脱离模型。图8为汽泡脱离前与燃料颗粒的相对位置，图9为汽泡的几何结构。汽泡受到浮力FB、表面张力FS、不稳定生长力Fdu、升力FL、拖曳力Fqs和惯性力Fbi等作用。汽泡所受合力∑F≥0时从颈部断裂，脱离孔隙。

ΣF=FB+FS+Fdu+FL+Fqs+Fbi

(28)

图8 汽泡与燃料颗粒间的相对位置Fig.8 The relative position of bubble and spherical fuel elements

图9 汽泡的结构Fig.9 The structure of bubble

(29)

(30)

(31)

(32)

(33)

(34)

其中，

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

3.2 汽泡脱离半径及其影响因素

颗粒大小、流速、壁温、压力等对汽泡的受力都有一定的影响，从而影响汽泡脱离半径。

3.2.1 颗粒半径

如图10所示，颗粒变大，汽泡脱离半径与颗粒半径之比(rd/Rp)减小。颗粒增大，孔隙增大，从而汽泡的体积增大，汽泡受到的浮力、表面张力等都增大。浮力与汽泡半径的三次方成正比，而表面张力与汽泡半径成正比，浮力增加的速度比表面张力快，所以rd/Rp随着颗粒增大而减小。

图10 不同流速下的汽泡脱离半径Fig.10 Bubble departure radius under different fluid velocity

3.2.2 液体流速

液体流速影响拖曳力，从而影响汽泡的脱离。在计算过程中流速很小，对汽泡受力的影响较小，故流速对汽泡脱离的影响不是很显著。如图10所示，在相同条件下，流速越大，汽泡脱离半径越小。流速增大，汽泡受到的液体拖曳力增大，从而加速汽泡的脱离，故流速越大，汽泡脱离半径变小。

3.2.3 压力

图11为相同流速及壁面过热度时，不同压力下的汽泡脱离半径曲线。其他条件相同时，压力越大，汽泡脱离半径越大。压力增加，蒸汽密度显著增加，汽泡惯性力增加，汽泡脱离半径增大。

图11 不同压力下的汽泡脱离半径Fig.11 Bubble departure radius under different fluid pressure

3.2.4 壁温

图12为不同壁面过热度时的汽泡脱离半径。壁面过热度越大，汽泡生长速度越快，汽泡生长力以及惯性力都增加，而汽泡生长力增加的更快，所以在其他条件相同时，壁面过热度越大，汽泡脱离半径越大。

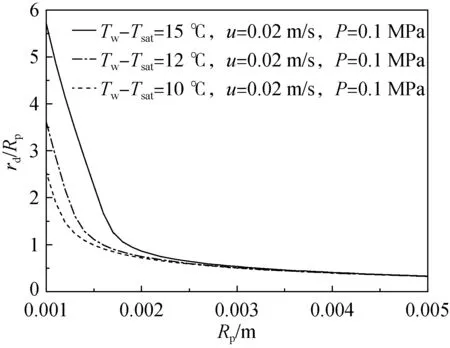
图12 不同壁面过热度下的汽泡脱离半径Fig.12 Bubble departure radius under different heated wall temperature.

4 结论

根据汽泡动力学原理及可视化试验结果，分别构建了球形燃料颗粒堆积的多孔结构内的汽泡滑移和脱离模型，对汽泡受力及传热进行了分析，通过计算得到了汽泡滑移临界曲率半径、汽泡脱离半径的变化规律。汽泡开始滑移时的临界曲率半径主要受颗粒大小影响，颗粒越大，汽泡相对临界曲率半径rcr/Rp越小，压力及流速也对汽泡临界曲率半径也有一定的影响。颗粒半径对汽泡脱离半径的影响最大，颗粒半径越大，汽泡相对脱离半径rd/Rp越小。流速、压力、壁面过热度对汽泡脱离半径也有影响，其他条件相同时，流速越大，汽泡脱离半径越小；压力越大，汽泡脱离半径越大；壁面过热度越大，汽泡脱离半径越大。

符号表

a——热扩散系数，m2·s-1；

CD——拖曳力系数；

CL——CL=1.2升力系数；

F——力，N；

Fdu——不稳定生长力，N；

FS——表面张力，N；

FB——浮力，N；

FL——升力，N；

Fcp——接触力，N；

Fqs——稳态拖曳力，N；

Fbi——汽泡惯性力，N；

g——重力加速度，m·s-2；

hfg——汽化潜热，J·kg；

K——导热系数，W·m-2·K-1；

L——气泡与颗粒接触线长度同，m；

m——质量，kg；

P——压力，Pa；

Qg——汽泡生长所需的热量，J；

QL,V——过热液体层与汽泡间的传热量，J；

QW,V——过热液体层与汽泡间的传热量，J；

r——半径，m；

RP——颗粒半径，m；

Re——Re=2ρLuLrb/μL雷诺数；

t——时间，s；

T——温度，℃；

ΔT——温差，℃；

u——速度，m·s-1；

ud——汽泡上升速度，m·s-1；

Vb——汽泡体积，m3；

hV——加热壁面与蒸汽间的换热系数，W·m-2·K-1；

h、h1、H、H1、H2、x、x1、y、r1、R2、r3、ri——几何参数。

希腊字母:

α——表面张力投影角；

β——侧面与汽泡中心线的夹角；

μ——动力粘性系数，N·S·m-3；

ρ——密度，kg·m-3；

σ——表面张力系数，N·m-1；

τ——时间，s；

τw——等待时间，s。

下标:

b——汽泡；

cr——临界状态；

d——汽泡脱离状态；

G，V——气相；

L，l——液相；

P——颗粒；

s，sat——饱和状态；

sup——过热状态；

w——壁面。