矩形巷道交岔口围岩应力随角度变化规律

罗海燕 谢财进 石 俊

（1、黔东南民族职业技术学院，贵州 凯里556000 2、贵州大学土木工程学院，贵州 贵阳550025）

1 概述

21 世纪以来，我国在地下工程方面的建设取得了很大进步。地下空间工程凭借其特有的优势，有效缓解了用地压力，无论是在空间利用，还是在环境保护等方面均起到了重要作用。在修建地下工程时，时常遇到一条巷道与另一条巷道两两交岔，在巷道交岔口处受力形式复杂，多次施工互干互扰，若未了解巷道交岔布设处围岩应力状态，冒然施工极易出现安全事故，故需对此展开研究。

由于巷道交岔区域的围岩极易发生应力集中，对围岩的稳定极为不利，是导致巷道破坏或坍塌的主要原因之一。因此，对该区域围岩稳定性的研究显得尤为重要。学者们对此也开展了诸多探究，但大多数是对交岔点处的支护、加固、施工等方面进行研究，而两巷道间相交角度变化对围岩应力影响的研究较少。陈珊等[1]结合理论分析、数值模拟和现场实测，研究T 型巷道交岔点围岩特征，并指出巷道断面、岩体强度、交岔角度和埋深等是交岔点失稳的主要影响因素，但并未对交岔角度进行深入探究。柴华彬等研究表明，与可控因素分岔角相比，埋深、平均侧压力系数、围岩强度对深部巷道交岔点的影响是显著的，而岩体强度则是影响深部巷道交岔点稳定性的最主要的因素，但是基于实际工程可知，当巷道用途和选址确定后，围岩力学参数、埋深及巷道尺寸等都是固定的，能够有效改变和控制的恰恰是分岔角度，故而需进行深入研究。张伟等[3]利用ANSYS软件计算分析了不同交岔角度顶底板应力分布情况及位移变化规律，得出巷道交岔点处锐角三角区域和钝角三角区域围岩角度的比值是判定巷道围岩稳定性的一个重要因素；同时，两者的比值还是判定巷道交岔点围岩应力集中程度的一个重要指标。

因此，本文以某地下工事为依托，就两巷道间交岔角度对交岔口围岩应力影响变化规律进行研究，建立巷道交岔口围岩应力的理论算法，再通过数值模拟对所构建的理论模型进行验证。

2 模型建立

巷道交岔口处的围岩应力状态是极为复杂的，为求解其交岔口力学特征，力学模型如图1 所示。

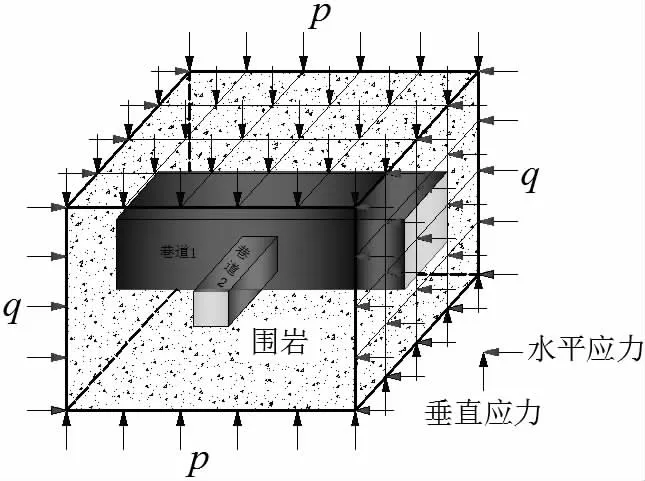
图1 巷道交岔口围岩受力分析图

巷道交岔岔口中心至塑性变形圈边界的距离：

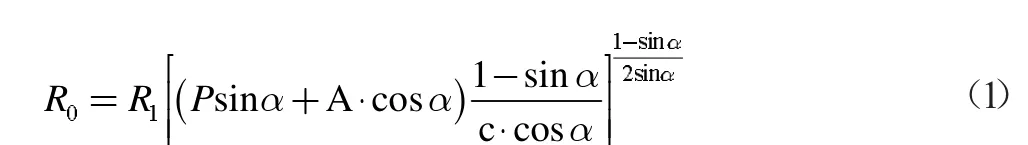
式（1）中：R1为矩形巷道1 外接圆半径；α 为巷道间的交岔角度（锐角）。

巷道交岔口围岩竖向应力σz为：

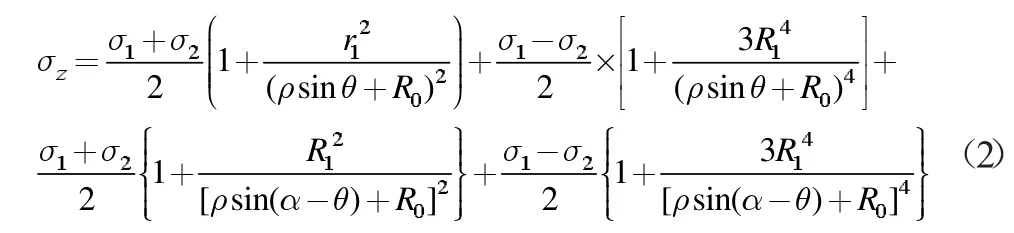
式（2）中：σ1、σ2为原岩竖向应力、水平方向的应力，且σ1=P，σ2=q=λP；ρ、θ 为极坐标参数。

化简可得得：

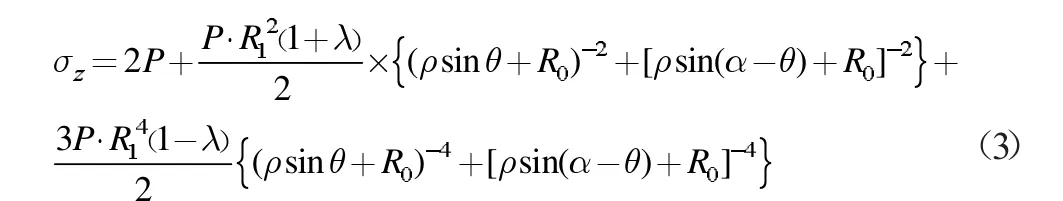
弹塑性极限平衡理论可知，弹性区围岩应力为：

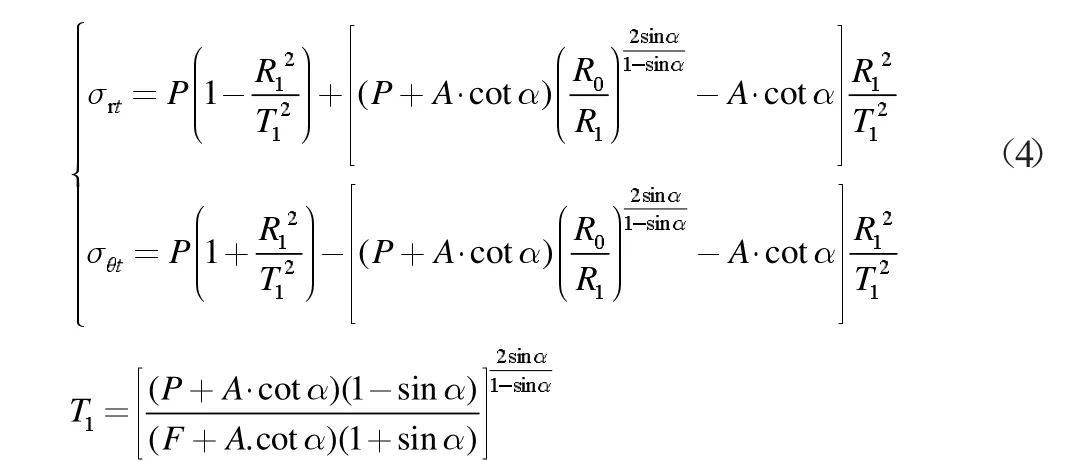
式（5）中：σrt为弹性区径向应力；σθt为弹性区环向应力；R1为松动圈半径; F 为支架反力。

由式（4）可进一步求取巷道交岔口沿水平方向的应力σx和沿巷道纵向的应力σy为：

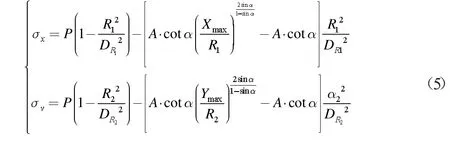
式（5）中，DR1、DR2为巷道1 和巷道2 的掘进距离；r2为巷道2 外接圆半径。

巷道交岔口围岩水平方向和铅垂方向的破坏深度：

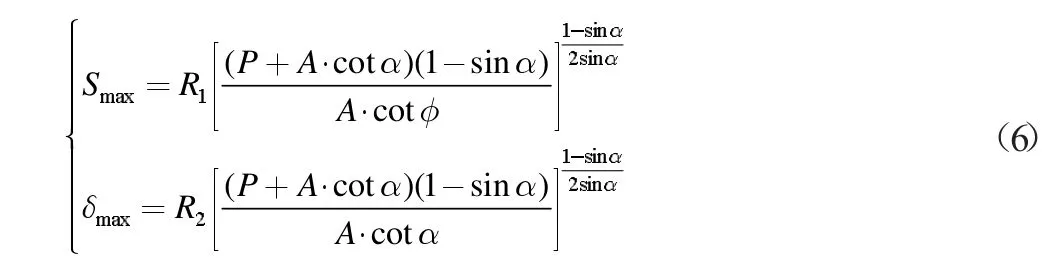
式（7）中：Smax、δmax 为巷道交岔口围岩水平及竖直方向的影响范围。

塑性区围岩应力可为：

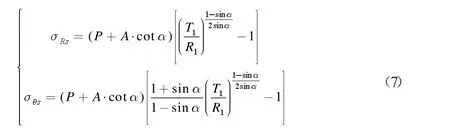
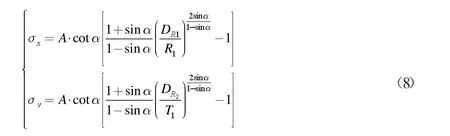
式（8）中：σRs为塑性区径向应力；σθs为塑性区环向应力。

经叠加后，塑性区交岔口围岩压力为：

3 数值分析

3.1 模型建立

现构建五种工况开展研究，两巷道间的交岔角度分别为10°、30°、50°、70°、90°（如图2 所示）。巷道尺寸为：高×宽=3.0m×4.5m，故而所构建的数值模型尺寸为长×宽×高=45m×45m×40m。两巷道间不同的交岔角度下围岩稳定性，仅作为规律性研究，故而为了研究简便，将各岩层做出如下处理，巷道顶部及以上岩层、底部及以下岩层全为砂质泥岩，煤层厚度4m，数值模型建立是将两巷道置于煤层中。

模拟基于有限元软件Madis GTS/NX，建立地下巷道交岔口数值模型，模型网格划分见图3。

3.2 应力分析

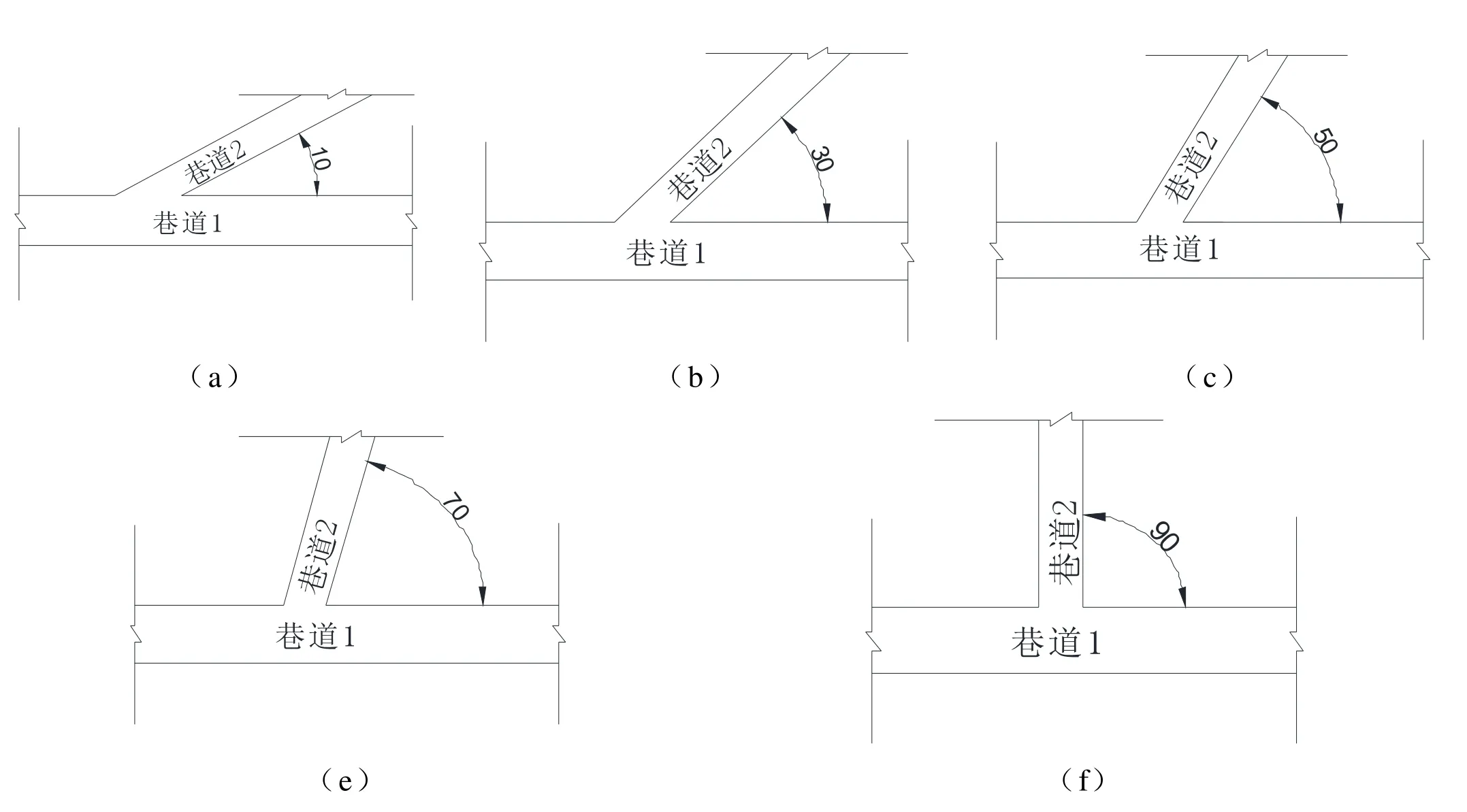
图2 拟建分析工况示意图

图3 巷道交岔口模型网格划分

由计算结果分析发现：

（1）无论两巷道间的交岔角度是多少，竖向应力都要大于水平方向的应力和横向应力，其值的大小为水平方向的应力、横向应力的2-3 倍。

（2）随着两巷道间的交岔角度由20°增加到90°，竖向应力呈现持续下降的趋势，交岔角度在10°-50°间变化时，竖向应力下降幅度较小，降幅为7.81%；交岔角度在50°-70°间变化时，竖向应力下降幅度较大，降幅16.95%；交岔角度在70°-90°间变化时，竖向应力值几乎没有发生变化。

（3）随着两巷道间的交岔角度由10°增加到90°，水平方向的应力呈现先增长后下降的趋势，交岔角度在30°-50°间变化时，横向应力增加，增幅为54.05%；交岔角度在50°-70°间变化时，水平方向的应力出现下降趋势，且下降幅度较大，降幅26.32%；交岔角度在70°-90°间变化时，水平方向的应力值降低，降幅16.67%。

（4）随着两巷道间的交岔角度由30°增加到90°，横向应力呈现先降低后增长再下降的趋势，交岔角度在30°-50°间变化时，横向应力降低，降幅为23.91%；交岔角度在50°-70°间变化时，横向应力出现增长趋势，增幅20%；交岔角度在70°-90°间变化时，横向应力值降低，降幅16.67%。不过从整体应力随交岔角度变化的趋势看，三个方向的应力值都呈现总体下降的趋势，只是竖向应力值总体变化较为明显，水平方向的应力和横向应力值仅是在小范围内波动。

基于数值模拟的五种工况，将相应数据代入弹性法和弹塑性法的理论计算，分析可知：三种计算方法的结果显示随着交岔角度增加，σx和σy的变化不大，特别是解析解结果变化微乎其微，而数值计算是基于实际工况进行模拟，其结果会在小范围内出现波动，这也进一步验证巷道交岔角度的变化对围岩σx和σy的影响较小。关于σx，基于弹性法、弹塑性法理论的解析解与数值计算结果间的最大误差分别为41.57%和14.00%；关于σy，基于弹性法、弹塑性法理论的解析解与数值计算结果间的最大误差分别为38.92%和13.67%。计算结果显示，在巷道交岔口围岩应力计算过程中，虽然弹性法与弹塑性法的计算结果都与数值结果接近，但是从计算精度考虑，弹塑性法更为精确。此外，随着巷道交岔角度的增大，σz的理论解的与数值计算结果变化基本一致，均呈现出逐渐减小的趋势，交岔角度的变化对σz的影响较大，解析法与数值计算间最大计算误差17.85。

4 结论

4.1 基于弹性法、弹塑性法构建巷道交岔口围岩应力计算模型，并与数值计算结果进行对比分析，交岔角度增加对σx和σy的影响较小，特别是解析解结果变化甚微，而数值计算是基于实际工况进行模拟，其结果则在小范围内出现波动。

4.2 关于围岩水平方向的应力σx，基于弹性法、弹塑性法理论的解析解与数值计算结果间的最大误差分别为41.57%和14.00%；关于沿巷道方向的纵向应力σy，基于弹性法、弹塑性法理论的解析解与数值计算结果间的最大误差分别为38.92%和13.67%。

4.3 随着巷道交岔角度的增大，σz的理论解的与数值计算结果变化基本一致，均呈现出逐渐减小的趋势，交岔角度的变化对σz的影响较大，解析法与数值计算间最大计算误差17.85%。

4.4 在巷道交岔口围岩应力计算过程中，虽然弹性法与弹塑性法的计算结果都与数值结果接近，但是从计算精度考虑，弹塑性法更为精确。