矿山深部巷道围岩变形与应力分布数值模拟研究

（河南工业和信息化职业学院，河南 焦作 454000）

在矿山深部工作中，由于矿山深部地形复杂的特点确保矿山深部巷道围岩的安全一直是矿山支护工作中最为薄弱的环节，因此长期以来受到同行学者们的重点关注[1]。在矿山开采过程中由于受到人为因素的影响，改变矿山深部巷道围岩结构，从而使矿山深部巷道围岩很容易发生变形，矿山深部巷道围岩变形容易引发安全事故问题，直接威胁矿山工作人员的生命安全。本文在此基础上，展开矿山深部巷道围岩变形研究，并通过应力分布数值模拟致力于精准掌握矿山深部巷道围岩变形情况，确保矿山深部巷道围岩的安全性。

1 矿山深部巷道围岩变形

在矿山深部开采过程中，原岩应力受开采影响会改变岩体的平衡状态，导致变形。矿山深部巷道围岩变形具体特征，如表1所示。

表1 矿山深部巷道围岩变形具体特征

结合表1所示，本文通过三方面分析矿山深部巷道围岩变形特征，为矿山深部巷道围岩支护工作的顺利开展提供理论依据。

1.1 巷道顶板的变形破坏

在矿山深部巷道顶板开挖过程中，巷道顶板由于受到应力产生瞬时弹性变形，并在变形时引发一系列其他继续变形[2]。在开挖后，巷道顶板的拉应力会集中致使围岩张拉破坏。这样一来，导致巷道顶板很难处于稳定状态，尤其在自重作用的促使下，巷道顶板的水平方向发育极其柔弱，形成数量、大小、形状各不相同的分离体。巷道顶板的变形破坏可以按照载荷方向分为：垂直载荷变形破坏以及水平载荷变形破坏，由于破坏方式的不同，巷道顶板的变形破坏所受载荷也必然不同。因此，在分析矿山深部巷道围岩变形时，必须考虑巷道顶板变形破坏的载荷方向。

1.2 角部破碎

矿山深部巷道围岩变形中，最先发生变形的区域往往在巷道围岩的四个边角处。考虑到矿山深部巷道围岩一般在比较狭窄的区域，因此只要一个角部出现破碎的情况，就会导致整个巷道围岩失稳，产生应力破坏，导致矿山深部巷道围岩变形。

1.3 巷道底膨破坏

巷道底膨指的是矿山深部巷道围岩的最底层，通常情况下为软弱岩层，在砂页岩互层层理的情形下导致巷道底膨破坏。结合冷建民等人提出的三山岛金矿深部巷道围岩破坏机理及支护参数优化中表明，影响巷道底膨破坏的直接因素为巷道底层的泊松比。当泊松比取值为0.5时，矿山深部巷道底板的挤压应力与竖直应力基本处于持平状态，此时压力系数为1。但一旦出现岩体的强度小于挤压应力时，就会造成巷道底膨破坏，进而引发矿山深部巷道围岩变形。

2 矿山深部巷道围岩应力分布数值模拟

考虑到矿山深部巷道围岩变形的各种形式，本文从矿山深部巷道的破坏模式入手，基本假定矿山深部巷道应力分布符合张拉剪切组合的Mohr-Coulomb准则，并且能够充分考虑到模拟围岩与支护结构之间的相互作用关系。在此情况下，分析模拟围岩与支护结构失效的破坏机理与过程，进而总结推导矿山深部巷道应力分布计算公式。最后，对矿山深部巷道应力分布数值模拟结果展开分析。

2.1 确定矿山深部巷道围岩应力应变关系

本文进行基本假定的具体内容包括：矿山深部巷道模拟围岩在应力应变过程中必须保持平面形态；排除由于抗拉强度的不同导致对数值模拟造成的误差值；在发生矿山深部巷道应力应变时，矿山深部巷道围岩变形应力与弯曲应变呈理想弹塑性关系，一旦承载力失效应力即保持不变以及矿山深部巷道围岩应力应变关系。可以将矿山深部巷道围岩应力应变关系视为一种曲线关系，如图1所示。

图1 矿山深部巷道围岩应力应变曲线图

在图1中，ε1指的是矿山深部巷道围岩应力直线部分合力；ε2指的是矿山深部巷道围岩应变直线部分合力；f0指的是应力应变曲线中二次抛物线矿山深部巷道围岩变形部分合力；gt指的是相关流动法则。通过图1可知，当矿山深部巷道围岩变形呈现双向应力状态时，围岩变形承载力必然会随着另一向围岩变形应力的增加而降低，直至围岩变形承载力失效。在得出围岩变形应力应变线性关系的基础上，可以根据计算结果曲线，总结出围岩变形抗压强度的计算公式。可以通过计算双向应力状态时，围岩变形的抗压强度，为下一步理论计算矿山深部巷道围岩应力分布做准备。设围岩变形的抗压强度为σ，则其计算公式，如公式（1）所示。

在公式（1）中，β指的是围岩所能承受的最大拉应力。根据多次计算，设围岩变形的抗拉强度为fc通常情况下为围岩变形抗压强度的10.5%～12.2%。因此，可以将围岩变形的抗拉强度模拟为：

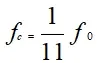
2.2 理论计算矿山深部巷道围岩应力分布

对应图1中，根据二次抛物线终点所对应的应变值，计算二次抛物线的高度即为围岩应力在应变值下的承载力。设围岩应力在应变值下的承载力为y，则其计算公式，如公式（2）所示。

在公式（2）中，x指的是围岩应力截面面积；r1指的是围岩应力的张拉强度。将得出的围岩应力分布在应变值下的承载力代入静力平衡条件可得，矿山深部巷道围岩应力分布计算理论模型M，如公式（3）所示。

在公式（3）中，b指的是矿山深部巷道围岩应力的摩擦角；a指的是粘聚力；n指的是膨胀角度，为实数。通过矿山深部巷道围岩应力分布理论计算模型中的自变量可以得出矿山深部巷道围岩应力分布的主要影响因素为矿山深部巷道围岩应力的摩擦角、粘聚力以及膨胀角度。矿山深部巷道围岩应力分布计算理论模型的整个计算过程均是以围岩应力分布平截面的假定作为基础，也就是说围岩应力分布截面各点应变与中和轴的距离必须为正比例，围岩应力分布应变与外围相应处的应变一致，在纵向受拉围岩应力达到屈服强度之前，截面的平均应变应该达到瞬间的平衡，以符合围岩应力分布平截面的假定。依据此假定，再结合静力平衡条件，建立了正截面围岩应力分布承载力的计算体系。为验证矿山深部巷道围岩应力分布计算理论模型的合理性，选取矿山深部巷道围岩，将得出的矿山深部巷道围岩应力分布数值模拟结果与实测围岩应力分布进行对比。从计算理论上来讲，利用FLAC3D内置的结构单元锚索单元（cable）来模拟巷道围岩支护中的锚杆和锚索，保证了矿山深部巷道围岩应力分布得以充分发挥，导致由于锚杆（索）与围岩的接触粘结性退化，应力逐渐均匀化，缓和了矿山深部巷道围岩应力轴向位移相应有轴向力，在一定程度上对模拟矿山深部巷道围岩应力分布是有利的。在本次模拟中，通过HISTORY命令设置变量来确定某处断面的位移变化和受力状态，也可以判断模型是否达到平衡或者破坏状态。因此，矿山深部巷道围岩应力分布数值模拟结果与实测围岩应力分布基本一致。

3 结束语

考虑到矿山深部巷道围岩变形问题的受到重视，矿山深部巷道围岩应力分布数值模拟经历了从起步到快速发展的阶段。

因此，本文对矿山深部巷道围岩变形与应力分布数值模拟研究是具有现实意义的，能够为解决矿山深部巷道围岩变形问题提供理论支持。

希望通过本文分析，为提高矿山深部巷道围岩安全性方面提供参考，以促进国家矿业的可持续发展。但本文唯一不足之处在于，没有对矿山深部巷道围岩变形控制技术进行深入分析，相信这一点，可以作为矿山深部巷道围岩变形领域日后的研究内容之一。