利用几何画板进行 初中生数学核心素养培养的探究
王梧 刘万中
摘要:几何画板作为信息技术环境下的一个应用软件,在初中几何教学和学习中可以落实多种初中数学核心素养的培养要求。为此,可以利用几何画板在课堂实践中进行发展几何直观、建立空间观念、强化推理能力、培养模型应用和创新意识等方面的探索。
关键词:初中数学;核心素养;信息技术;几何画板;数学实验
为落实初中生数学核心素养的培养,六安市清水河学校承担了六安市教育信息技术研究2019年度课题“信息技术环境下的初中数学核心素养培养的研究———以初中数学实验为例”。几何画板作为初中数学课堂教学的一个高效软件,备受数学教师和学生的关注和欢迎。课题组以几何画板为载体开展初中数学实验,进而落实对初中生数学核心素养的培养要求。本文对课题组的前期研究成果进行小结,以期同人批评指正。
一、利用几何变换发展几何直观和空间观念
义务教育沪科版初中数学教科书“14.2命题与证明”中安排了让学生探究“三角形的内角和等于180°”的活动。通过传统的剪纸和拼图的实验活动,学生可以直观地观察到三角形的三个角可以共顶点地拼成一个平角,从而得出“三角形的内角和等于180°”的结论。这个结论也可以通过度量来获得。但传统的操作,无论是度量还是剪拼,学生都难以获得准确的180°,而且学生在操作过程中也难以获得进行推理的直接启示。在教学中,笔者考虑到学生在小学阶段就已经了解了这个结论,而且能进行简单的应用,所以在课堂上没有让学生再进行度量和剪拼的操作,而是让学生把注意力集中到观察和思考中,观察三个内角剪拼后所形成的图形,然后让学生思考该图形是通过什么样的几何变换得到的。在多数学生苦思不得其解的情况下,笔者通过几何画板演示将∠2绕AC中点旋转180°和将∠3沿BC平移而获得该图,使得学生豁然开朗,进而引发了学生进行推理论证的热情,整个教学过程高效有趣,学生兴趣盎然。
二、通过构建轨迹,强化推理能力和模型应用意识的培养
初中数学大量涉及动点运动探究问题,因该类问题立足于基本图形,但灵活多变,思维容量大,所以历来被作为培养数学能力和思维能力的良好载体。但动点运动的状态隐而不显,让人捉摸不定,多数学生因在学习上有畏难情绪或几何直觉不强、推理能力较弱,在面对该问题时往往是一筹莫展。
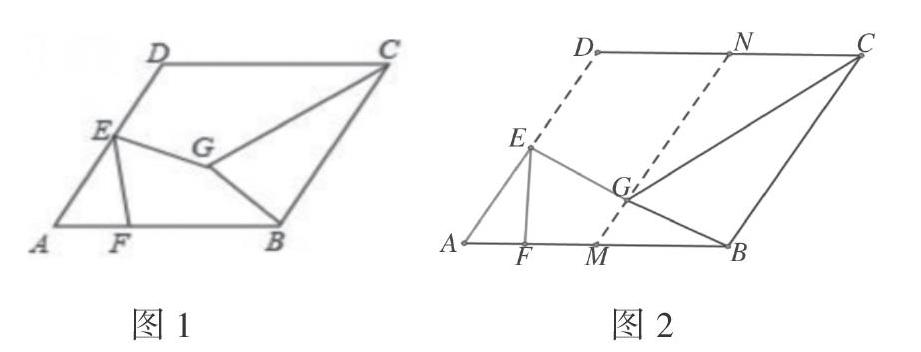
在教学中,笔者曾组织学生讨论过该类问题,以其中一例阐述之。如图1,菱形ABCD的边长为4,∠BAD=60°,E是边AD的中点,F为边BC上的一个动点,EG=EF,且∠GEF=60°,则GB+GC的最小值是多少?
多数学生在“两定一动、求最小值”的条件启示下,能较自然地联想到该问题应该属于或最后能转化为“将军饮马”模型求解。“将军饮马”问题的核心是动点的轨迹为直线或线段,而本题中动点G运动后所形成的轨迹是难以判断的,学生一时陷入困境。在课堂上,不少学生都能主动拿起直尺和圆规等作图工具,不停地尝试,经历了多次操作后,仍是找不到突破口。此时,笔者利用几何画板展示点G的运动过程。利用几何画板构造轨迹的操作,将通过传统实验操作难以获得的结果在信息技术的帮助下实现了可视化,形成了如图2所示线段MN。笔者运用信息技术手段瞬间降低了思维难度,实现了数学思维的可视化,这是传统的教学手段难以实现的。信息技术支持下的数学实验,不仅使得实验结果更直观、探究更高效,而且能在实验操作过程中寻找和发现形成数学结论的原理,引发数学思考。该题通过几何画板的操作,发现点G运动后形成的轨迹是线段MN。学生凭已有的几何直觉,感知该问题可以转化为“将军饮马”模型,线段MN所在的直线成了对称轴,将图形沿直线MN折叠后,发现点B与点E重合,线段GB与GE重合,从而得出GB=GE,进而将求解GB+GC最小值问题转化为GE+GC最小值问题。通过在直线MN上移动点G的位置,可知当点C、点E和点G三点在同一条直线上时,GE+GC的值最小。笔者通过几何画板的实验探究,使学生获得了解题思路,同时使学生的推理能力和模型应用意识得到了较好的培养,也使信息技术与数学学科进行了深度融合。
三、利用实验结果的多样性,落实创新意识培养
通过几何训练能实现思维训练,通过变式训练能培养思维的敏捷性和思辨性。进行几何变式训练是我国基础教育的优良传统,积累了大量的经验可供借鉴。然而相伴而生的应试教育也暴露出了不少弊端,教学中经常出现“去头去尾烧中段”的做法。更有甚者,只是让学生记住结论,然后大量地套用结论。这种教法和学法会让学生逐渐丧失学习几何的兴趣,甚至会发展到厌恶数学的地步。
如何利用好几何变式教学和训练,达到变式教学本真的目的,这是笔者从教以来一直思考的问题。笔者在教学中也在不断地大胆实践,希望能突破困境。利用几何画板动态地展示问题的“前生与后世”,找准问题的生长点,引导学生观察思考,大胆猜想,小心求证,常能激发起学生的好奇心且能较长久地保持学生的探究欲,实现发展学生数学核心素养的目的。
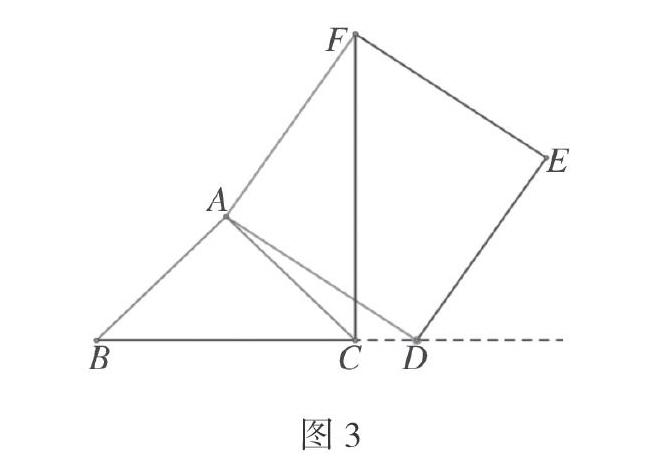
例如,在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合)。以AD为边作正方形ADEF,连接CF。首先进行操作1:在几何画板中拖动点D的位置,使点D在线段BC上,引导学生从位置关系和数量关系两方面去观察,大胆说出自己的猜想。在大家热烈的讨论下,经过多轮争辩,最后得出两个重要的猜想:①BD⊥CF;②CF+CD=BC。笔者在肯定了这两个猜想后,向学生提出了该如何证明的问题。在片刻的思考后,不少学生发现了△ABD=△ACF,从而找到了证明的关键。其余学生也恍然大悟,接着都完成了证明。
接着进行操作2:在直线BC上拖动点D的位置,改变图形的形状。学生看着变化的图形,面面相觑。此时,笔者抛出问题:在图形的变化中,你有什么发现?能够提出什么问题?学生根据以往的学习经验,提出在图形的变化过程中是否存在不变量。结合第一次操作,学生提出来操作1中的两个结论是否还成立。如图3所示,当点D在线段BC的延长线上时,结论①仍成立,结论②不成立。那么,CF、BC、CD三条线段之间又蕴含着怎样的数量关系呢?通过观察不难发现:CF=BC+CD。通过△ABD=△ACF,不难证明发现的结论。
在完成操作2的探究后,笔者引导学生思考:还可能有什么样的操作?对应的图形会是什么?有一些学生经过自主探究,画出了对应图形。此时,笔者利用几何画板进行操作3:将点D拖至线段BC的反向延长线上,“在其他条件不变的情况下,CF、BC、CD三条线段又有着怎样的数量关系”等问题自然生成,学生的探究水到渠成。
利用几何画板进行一系列实验结果多样性的操作探究,不仅使学生获得了变式训练的效果,更让学生掌握了研究数学、发现新结论的常用方法和途径。学生乐于探究,较为持久地保持了探究的兴趣。
(本文系六安市教育信息技术立项课题“信息技术环境下的初中数学核心素養培养的研究”的阶段性研究成果,立项号:LA201920)
参考文献:
[1]高茂军.核心素养引领下的课堂教学革新[M].天津:天津教育出版社,2018.
[2]马复.新版课程标准解析与教学指导:初中数学[M].北京:北京师范大学出版社,2012.
[3]刘须群.信息化背景下的案例教学设计研究[D].上海:华东师范大学学报,2005.
(责任编辑:韩晓洁)

