浅谈人工神经网络

赵钰

1 引言

1.1 背景

如上图所示，分别是夜景、狗、百合花的照片，我们可以快速准确的识别出来，并且通常不会出错。但是对于计算机而言，并不会很容易的识别出，甚至会非常困难。

然而，计算机可以在1秒内计算出超级复杂的数字，而我们口算两位数乘法都会比较困难。

因此，对比计算机与人类，发现：

就此发现，我们可以推测图像的识别需要人类的智慧才可以解决，这才是人工智能的精髓。因此，我们就要找到新的算法赋予计算机，使他可以解决那些需要用到人类智慧的问题。

1.2 目的。1、识别手写数字，比如说书写者由于字迹潦草写出的“4”、“9”分不清，利用神经网络分析具体是哪一个数字。2、识别长文本，比如说打开一个超级多数据的文本，其中的数据用逗号隔开，我们无法识别数字的排列规律以及数据个数，因此要使用计算机识别。并给出其排列规律等需求。

2 建立神经网络

2.1 神经元。神经元是生物大脑中最基本的单位。他的传递方式就是将电信号从这一端传递到另一端，再沿着轴突，将电信号从这一树突传递到另一树突。这就实现了将这个信号从这一神经元传递到下一个神经元。经过这样一个个过程的传递，我们便有了感知声、光、电、热等信号的能力，我们便有了视觉、嗅觉、听觉、触觉等。而我们的大脑主要就是由神经元构成的，大约有1000亿个神经元。

2.2 权重。权重最重要的作用就是可以调节每一个节点之间连接的强度。权重越大即这两个节点之间的连接就越强，也就是说要放大信号;权重越小，即两个节点之间的连接就越弱，也就说要缩小信号。

2.3 搭建神经网络。搭建一个神经网络，至少需要以下三个函数：（1）初始化函数——设置节点的数量，包括输入层节点、隐藏层节点、输出层节点（2）训练——让机器学习给定的训练集样本，并将所给出的权重进行优化（3）查询——给定一个输入值，得出一个输出值。

3 手写识别

我们将数据文件保存在“mnist_dataset”文件夹中，下面进行读取数据并展示。

Data_file=open（“mnist_dataset/mnist_train_100.csv”，r）  （打开文件<路径>，并且是只读的模式）

Data_list=data_file.readlines（） （读取文件）

Data_file.close （关闭和清理文件）

在anaconda中跑一下，得出：

由上图可观察到，这是一个长度为100的列表，第一个数字是“5”，这可以看作是一个标签。同时我们可以看到其他的784个数字是构成图像像素的颜色值。且颜色值的范围为[0，255]。

下面我们就要将使用上图所示的数组进行绘图：

Import numpy

Import matplotlib。Pyplot

%matplotlib inline

All_values=data_list[0].split（‘，）  将长的字符串进行拆分，并且打印出来

Image_array=numpy.asfarray（all_values[1：]）.reshape（（28，28））   要使用除了列表中的第一个数字外的所有数字，并且将这些字符串都转化为实数，而且要创建数组。将这个数组美经过28个数字就折返一次，最终形成一个28*28的正方形矩阵

Matplotlib.pyplot.imshow（image_array，cmap=Grey，interpolation=None）   将输出的画布颜色调为灰色，以便更好地展示结果。

3.1 MNIST训练数据

首要的是要将颜色的值进行整改，我们将较大的数字进行缩放，将[0，255]这一范围缩放为[0.01，1.0]，最低点选为0.01是为了避免最小值为0最终造成权重自动更新失败。所以要将[0，255]范围内的数值同时除以255，得到[0，1]，再乘以0.99，将范围变到[0，0.99]，最后再加上0.01，最终得到范围是[0.01，1.0]。

Scaled_input=（numpy.asfarray（all_values[1：]）/255.0*0.99）+0.01

Print（scaled_input）

对于激活函数而言，若输出值为0或1时，会是权重达到饱和状态，使激活函数失效，因此我们将用0.01和0.99去替代0和1，这样“5”的数组应该由原来的[0，0，0，0，0，1，0，0，0，0]显示为[0.01，0.01，0.01，0.01，0.01，0.99，0.01，0.01，0.01，0.01]。构建目标矩阵：

# output nodes is 10 （example）

Onodes=10

Targets=numpy.zeros（onodes）+0.01

Targets[int（all_values[0]）]=0.99

3.2测试网络。我们想要测试之前训练的效果，获取数据集：

# load the mnist test data CSV file into a list

Test_data_file=open（“mnist_dataset/mnist_test_10.csv”，r）

Test_data_list=test_data_file.readlines（）

Test_data_file.close（）

最后得出准确率为60%。

3.3 完整训练集。下面我们将进行完整的训练，用60000个训练样本来完成三层神经网络的训练。

如上图所示，我们可以观察到准确率高达了94.73%，由此我们可以认为其准确率已经是非常高的了！

4 模型改进

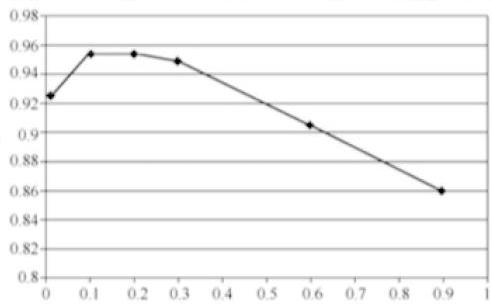
4.1 调整学习率。我们想提高准确率，首先想到的是调整学习率。我们先将学习率翻倍成0.6，但得到的结果不尽人意，最终准确率只有90.47%。于是我们决定降低学习率，将其值设为0.1，通过计算得到准确率为95.23%。再一次降低学习率至0.01，发现准确率下降至92.41%。因此，我们推测学习率对准确率的影响是一条变化的曲线，是存在峰值的。因此，绘制了学习率与准确率的图像：

根据上图发现，学习率大概在0.2的时候，其准确率最高。

4.2 改变隐藏层节点数量。我们还可以通过改变隐藏层节点的数目来改变整个神经网络的形状，从而也达到提高准确率的目的。

之前上文中我们所运用到的隐藏层的节点全部为100个，接下来就要减少、以及增加节点，来观察准确率的变化。

经过计算统计，若隐藏节点的个数为5个时，准确率大约为70%，而增加到200个节点时，准确率增加到97.62%.绘制图像如下：

观察上图可以看出，隐藏节点大约在200个时，便可使准确率达到最高。

5 结论

训练神经網络进行手写识别，通过进行调整学习率和隐藏层节点个数可以大幅度提升识别的准确率。通过三层神经网络与数据集不断计算，使神经网络具有学习功能。使用不同的激活函数也会有不同的效果。