渠道走向及几何尺寸对灌溉水增温的影响

郭佳雯，蒲迅赤，黄瑞仙

（四川大学 水力学与山区河流开发保护国家重点实验室，成都 610065）

0 引 言

【研究意义】农作物生长和发育都需要一定的环境温度，温度是决定农作物生长环境优劣的重要条件之一[1-2]。如果在灌溉过程中水温过低，将会降低植株的光合作用，抑制根系吸水，影响矿物质的吸收，从而打破农作物的发育规律，最终导致粮食减产，这在国内外许多国家都有实例[3,6]。因此，必须采取一定措施提高灌溉水温，而探究灌溉水温的影响因素是提高灌溉水温的前提。

【研究进展】在我国，北方高寒水稻种植地区普遍采用井水进行灌溉[6]，但因气候原因，该地区井水温度一般较低，远远达不到水稻的适宜生长水温甚至最低生长水温，使水稻出现生长缓慢、返青慢、抽穗晚、易贪青晚熟、分蘖率低、成穗率低、结实率低、干粒质量下降、机体发育不良、易于倒伏等不良生长现象[7,10]，严重降低了种植水稻的经济效益。

与北方的井灌种植水稻不同，南方水稻种植地区主要利用水库蓄水灌溉水稻—将水库的水引入渠道，通过渠道将水引入农田。但是大型水电工程的建设，特别是高坝大库，改变了河道的水温过程，在灌溉季节，受太阳辐射、对流混合和热量传输的影响，水库出现明显的水温分层[11,14]。而水电站出于发电目的往往设置高程较低的单层泄水口[15]，分层型水库下层水体常年维持低温状态，因此造成水库下泄水温低于原河道天然水温，利用这些下泄的低温水灌溉农田同样会对农作物的生长产生不利影响，如使植株光合作用减弱、吸肥能力下降、水稻成熟减缓、结实率低、产量下降，引发冬小麦的早熟等[16]。因此，如何提高灌溉水的温度，从而达到农作物生长最适水温，是一个亟待解决的工程问题。

现有的灌溉水增温措施主要分为3 种：工程增温、设备增温和水管理增温[2]。工程增温方式有晒水池增温、修筑过水子碾、升温田和延长灌溉渠道增温[17]，其中晒水池增温是最常用的增温手段，即将井水先引入占地面积较大的晒水池中，利用太阳辐射使灌溉水温提高到一定的温度，再将增温后的水引入稻田以达到水稻在适宜水温中生长的目的[18]。过水子碾的增温效果相对于延长渠道增温效果提高了6 倍，其他工程增温设施效果不明显[1]。设备增温有宽浅式渠道覆膜增温、叠水板增温、晒水池内铺设晒水板增温、雾化增温、增温棚增温等，设备增温效果明显，增温幅度达3～5 ℃[8,10]。水管理增温方式通过管理灌溉水水层厚度、流量及灌溉方式等手段增温[19,22]。在上述增温措施中，增温效果显著的晒水池主要是利用太阳辐射和热量交换这些自然因素进行增温，修筑过水子碾增温是通过延长水路从而加长热交换的时间达到水体增温的目的。

从以上研究可以发现水气温差和太阳辐射对水体增温过程有重要的影响。渠道在运送灌溉水的过程中，水体会接收太阳辐射，同时与空气进行热交换。然而渠道宽深比、走向的不同，会导致水体输运过程中接收太阳辐射的面积不同，因此渠道的走向和宽深比可能会影响增温效果。【切入点】目前鲜有报道从渠道尺寸和走向方面研究其对灌溉水温的影响，因此本文从水体热量交换的基本理论出发，采用理论与试验相结合的方法。【拟解决的关键问题】研究渠道走向和几何尺寸对灌溉水自然增温效果的影响规律和影响程度，为农业生产中灌溉水增温措施提供一定参考。

1 模型建立

1.1 热通量计算

热通量计算公式参考《水电水利建设项目河道生态用水、低温水和过鱼设施环境影响评价技术指南（试行）》，包括净太阳短波辐射、净长波辐射、蒸发、传导和固热交换5 个方面，进入水体的热通量计算式为：

式中：φsn为太阳短波辐射（W/m2）；φan为大气长波辐射（W/m2）；φbr为水体长波的返回辐射（W/m2）；φe为水面蒸发热损失（W/m2）；φc为热传导通量（W/m2）；φd为水固热交换（W/m2）。

①水面净吸收的太阳短波辐射φsn计算式为：

式中：φs为到达地面的总太阳辐射量（W/m2）；β1为太阳辐射的表面吸收系数；γ为水面反射率，与太阳角度和云层覆盖率有关。

②大气长波辐射φan计算式为：

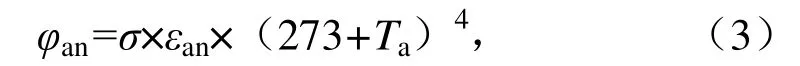
式中：σ 为Stefan-Boltaman 常数，等于5.67×10-8W/(m2·K4)；εan为大气发射率，计算式为：

式中：Ta为水面上2 m 处的气温（℃）；Cr为云层覆盖率；ea为水面上空气的蒸发压力（hPa），可由气温Ta计算：

式中：hum 为相对湿度。

③水体长波的返回辐射 φbr，其强度可用Stefan-Boltzman 定律计算：

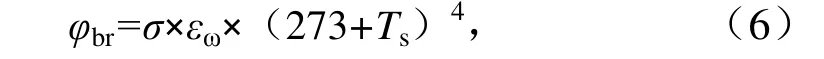
式中：Ts为水表面温度（℃）；εω为水体的长波发射率，一般取0.965。

④水面蒸发热损失φe采用《工业循环水冷却设计规范》推荐的公式计算：

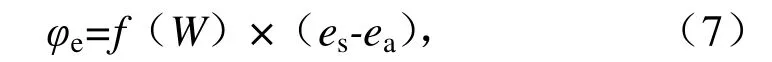
式中：f（W）为风函数（W/（m2·hPa）），反映了自由对流和强迫对流对蒸发的影响，计算式为：

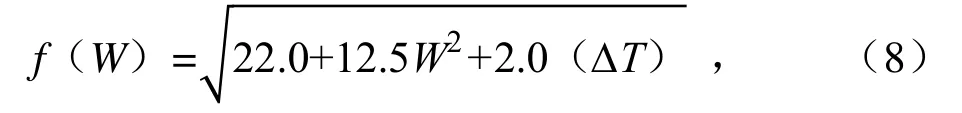
式中：W 为水面上10 m 处的风速（m/s）；ΔT 为水气温差（℃）；es为相应于水面温度Ts的紧靠水面的空气饱和蒸发压力（hPa），计算式为：

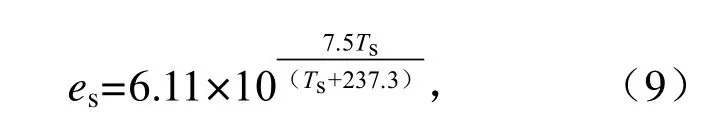
⑤热传导通量φc计算式为：

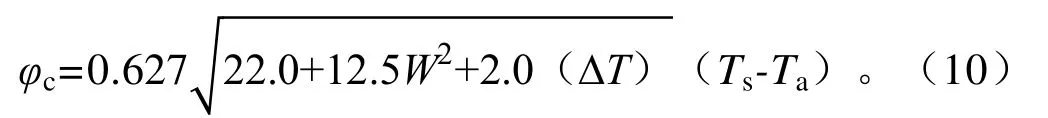
⑥水固热交换φd

渠道固体边壁的温度与水的温度存在一定差值，由于温差造成热传导，属于水固界面的热交换。由于本试验中避免了试验装置与四周及地面的热交换，故在此不对水固热交换进行计算。

1.2 渠道表面接收太阳辐射面积计算

渠道接收太阳辐射面积如图1 所示。从图1 可以看出，假定灌溉渠道的长度为L，宽为B，高为H，渠道与东西方向的夹角为β，当水深为h，太阳高度角为α 时，根据几何关系得出渠道表面受光照面积，推导过程如下：

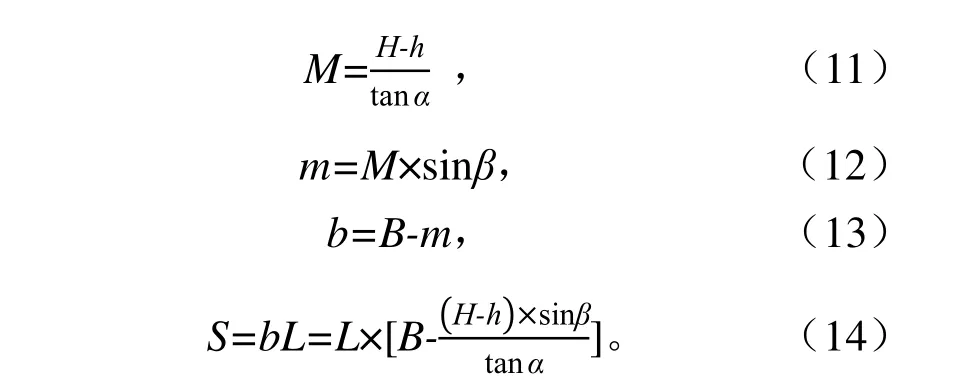
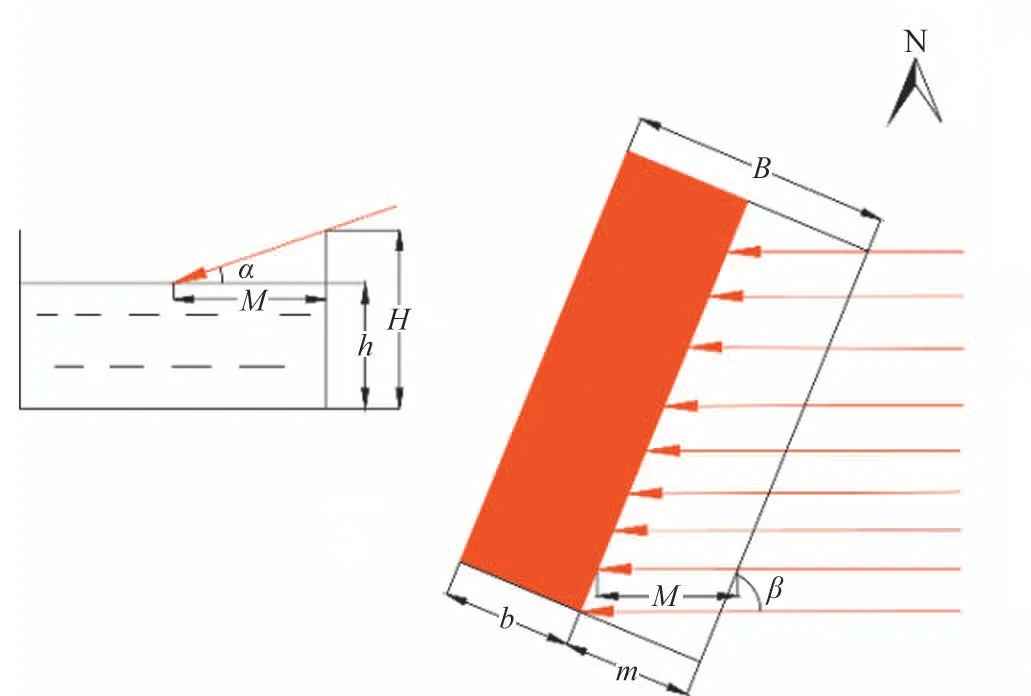
图1 渠道接收太阳辐射面积示意 Fig.1 Schematic diagram of solar radiation area received by channels

1.3 水表面温差计算

对于面积为S 的水面，经过时间间隔t，传导的热量计算式为：

而热量的传递必然导致温度的变化，它们之间的关系是：

式中：c 为水的比热容（J/（kg·℃）），取4.2×103J/（kg·℃）；m 为水体质量（kg）；T1、T2分别为初始水温和经过时间t 后水体的温度（℃）。

因此，对于一个确定面积、质量和热通量变化的水体，理论上可在时间t 内计算出其温度变化量ΔT，即：

由于式（15）是基于水体表面所有面积接受光照的条件下进行计算的，适用于天然湖泊或水库。而对渠道来说，太阳照射的角度和渠道的高度及水深会使水面一部分面积处于阴影中，接受太阳辐射的水面积会减小。因此在渠道水体表面温度变化的计算中，应把式（14）中的水面积S 运用到式（17）中进行修正。

2 模型验证

2.1 试验装置及仪器

1）水槽：2 个长方体透明塑料水槽模拟灌溉渠道，1 号长型水槽的尺寸为长度220 cm、宽度20 cm、高度28 cm；2 号长型水槽长度200 cm，宽度20 cm，高度30 cm。为还原灌溉渠道的实际情况，用内外墙屋面隔热保温挤塑聚苯乙烯泡沫板包裹水槽侧面及底部。

2）自动式温度记录仪：用于自动测试各个水槽24 h 的水温，本次试验记录间隔为30 min。

3）50 ℃量程温度计：用于校正自动温度记录仪。

4）PC-4 型便携式自动气象站：气象站位于四川大学水利水电学院天台，该处日照情况良好，距四周建筑物有足够的距离，可观测得到准确的气象数据。

2.2 试验方案

将2 个透明的塑料水槽放置在采光良好的天台上，槽中水体为一定体积的静止水体，将ZDR 仪器放在水体表面以在试验过程中测量水面的温度。试验中将渠道的走向分成4 种情况：①与东西方向成60°，②与东西方向成45°，③与东西方向成30°，④与东西方向成10°。每种情况进行2 个日照日以上的观测，如试验日云量较大或阳光不够充足，可增加试验天数，最后选取太阳辐射较强、云层覆盖率较少的时段数据进行计算。试验时，记录水槽各个时段对应的水深，每3 h 记录1 次。此外，还需根据气象站获取每日气象数据。最后运用式（1）—式（17）进行每日理论水温温差计算，并与实测的每日水温温差进行比较。

2.3 模型系数选取

1）表面吸收系数β1。与水的浊度有关，一般在0.4～0.7 之间取值[23]，经多次试算，取为0.7。

2）水面反射率γ。孙志方[24]曾在晴朗天气下对较为清澈的池塘进行研究，得出了水面反射率随太阳高度角变化的曲线。由于本试验在阳光充足、天气晴朗的条件下进行，且水槽内的水质清澈，试验条件很相似，故有理由依据其水面反射率-太阳高度角曲线进行取值。

太阳高度角α 计算式为：

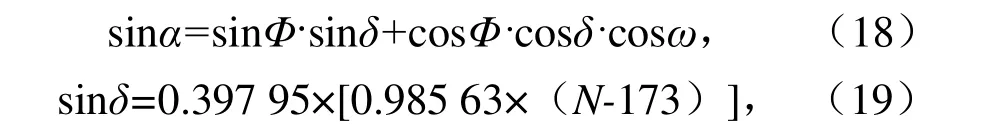
式中：δ 表示太阳赤纬（即太阳直射点纬度），太阳赤纬与地理纬度一样，都是以北纬为正，南纬为负；Φ表示观测地地理纬度；ω 表示地方时（时角），以正午12:00 是0°为基准，上午为负，下午为正，每个小时为15°进行计算；N 为1 年中的日数，从每一年的1 月1 日开始起算。

试验地点的地理纬度为北纬30°37＇41″，即30.63°，则有：sinΦ=0.51，cosΦ=0.86。

由于试验期间，水面反射率随天数变化非常微小，所以试验期间每天各个时刻的水面反射率取值相同：06:00 和18:00 的水面反射率为0.38；09:00 和15:00的水面反射率为0.08；12:00 的水面反射率为0.068。

由于各个时刻气象条件均在发生变化，在计算某个时段的热通量变化时，对具有连续变化的数据取该时段内的平均值。而离散的数据以各时段初始时刻的值带入公式计算，例如本试验中云层覆盖率是根据网站WORLD WEATHER ONLINE[25]所得，每3 h 有1 个数据，此时取初始时刻的云层覆盖率进行计算。

2.4 结果与分析

1 号、2 号水槽的温差计算结果如表1 所示。从表2 可以看出，1 号水槽在试验期间最大计算温差为5 月7 日的11.55 ℃，最小计算温差为5 月1 日的1.11 ℃。最高绝对误差为5 月2 日的5.34 ℃，最低绝对误差为5 月7 日的-0.35 ℃，相对误差在5.80%～60.22%之间，其中最大相对误差出现在5 月1 日，最小相对误差出现在5 月7 日。

2 号水槽在试验期间最大计算温差为5 月6 日的11.04 ℃，最小计算温差为5 月1 日的1.01 ℃。最高绝对误差为5 月7 日的-2.19 ℃，最低绝对误差为4 月29 日的0.06 ℃，除了5 月1 日阴天太阳辐射很低导致相对误差高达57.93%外，其他日期的相对误差最高为29.16%，最低相对误差为0.63%。

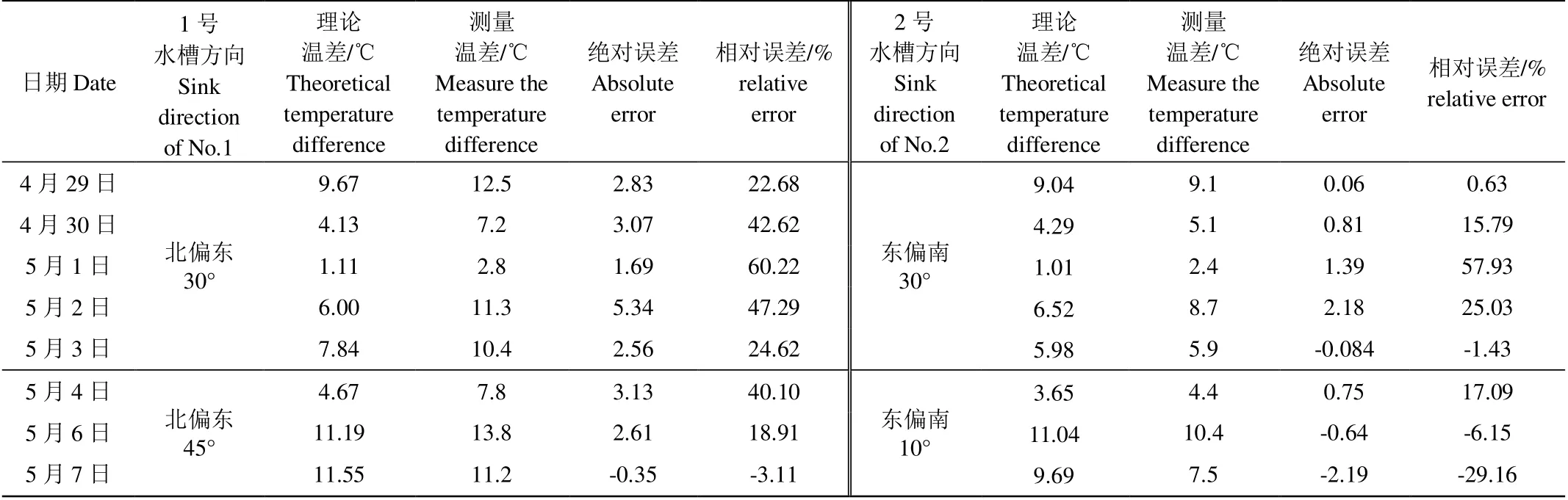
表1 1 号、2 号水槽温差计算结果 Table 1 Temperature difference calculation results of No.1 and No 2 water tank

整体来看，测量温差较理论温差偏高，存在一定的误差。1 号水槽5 月7 日测量温差值和理论温差值基本重合，5 月1 日和5 月2 日测量值和理论值有较大偏差，但总体变化曲线和变化趋势一致；2 号水槽理论计算温差与实际温差比较接近，特别是4 月29日、4 月30 日、5 月3 日、5 月4 日和5 月6 日基本重合。分析造成测量温差和理论温差间偏差的原因包括：①读数因素。俯视或仰视会造成读数的偏高或偏低；当风速较低，云量较多时，水蒸发较慢，水深变化不明显，从而观测不出读数变化；除此之外，卷尺精确度有限，当水位变化在1 mm 之内，很难肉眼观测出来。②试验装置因素。试验中虽然用保温隔热的聚苯乙烯泡沫板包裹了水槽四周及底部，但泡沫厚度不够，与空气接触的泡沫外侧温度较高，将热量传至泡沫内侧，使水槽内水体与四周空气及地面存在一定的热交换，导致测量温差相对于理论值偏高。③计算取值因素。试验中观测的气象数据、水深数据与时刻对应，而在计算时，需要计算出一个时段的热通量变化，这便需要取一个时段内的平均值进行计算。这是造成测量温差值与理论温差值间误差的重要原因。此外，气象站的云量数据是每隔3 h 的观测值，无法取平均值，因此只能取某一时段的初始云层覆盖率代入公式计算，造成一定的偏差。

1 号水槽的理论温差值与实际值之间有一定误差，但其变化趋势一致，2 号水槽的理论温差与实际值较为接近且变化趋势一致，可以证明前面的计算模型具有一定的精度，在渠道的设计中可利用此公式作为指导。

3 渠道走向及几何尺寸对灌溉水增温的影响

在验证模型正确的基础上，进一步运用渠道水体升温公式讨论不同的渠道走向、渠道宽深比对渠道水增温的影响。分别以渠道宽深比、渠道走向为自变量，计算在流量Q、水体质量m、渠道开挖横截面面积A、水体流经距离l、渠道糙率n、渠道坡降i 一定的情况下，各个情况之间水体增温的差别。

首先选定模型渠道流量Q 为0.08 m3/s，糙率n为0.02，渠道坡降i 为0.005，则根据水力学明渠流均匀公式[26]，有：

式中：Q 为渠道流量（m3/s）；v 为断面平均流速（m/s）；A 为渠道过水断面面积（m2），其中流速可用谢齐公式表示为：

式中：n 为渠道糙率；R 为水力半径（m）；i 为水力坡降。

式中：B 为渠道宽度（m）；h 为过流断面水深（m）。

保持渠道走向等其他条件一定，当渠道宽深比分别为2∶1、1.5∶1、1∶1 时，根据式（20）—式（22）对渠道相关尺寸进行取值，结果如表2 所示。

表2 各宽深比对应量值 Table 2 Corresponding value of width depth ratio

取5 月3 日的气象数据计算在各时段各渠道走向下不同渠道宽深比的增温幅度。为保证各种情况只受自变量的影响，取水体质量均为100 kg，即水体体积均为0.1 m3，流经渠道长度1 000 m，初始水温均为5月3日上午09:00的水温20 ℃。计算结果如表3所示。

从表3 中可以看出，同一走向中，宽深比越大，渠道的增温效率越高。渠道宽深比为2∶1 时增温幅度最大，其次是1.5∶1，增温幅度最小的是宽深比为1∶1 的渠道；渠道宽深比相同时，走向不同增温幅度也不同，东西走向的增温幅度最大，其次是与东西方向成45°夹角时，南北走向的增温幅度最小。

表3 渠道水增温幅度计算结果 Table 3 Results of channel water temperature rise range ℃/km

当渠道走向相同，宽深比不同时，比较不同宽深比对灌溉水自然增温效果的影响。以上午09:00 为例，当渠道走向均为南北方向时，渠道宽深比为2∶1时增温率为0.089 ℃/km，1.5∶1时为0.061 ℃/km，1∶1 时为0.025 ℃/km，宽深比为2∶1 的渠道同样条件下比宽深比为1∶1 的渠道增温率高0.064 ℃，经10 km 可高0.64 ℃，高出256%；当渠道走向均为与东西成45°夹角时，渠道宽深比为2∶1 时增温率为0.105 ℃/km，1.5∶1 时为0.079 ℃/km，1∶1 时为0.047 ℃/km，宽深比为2∶1 的渠道在同样条件下比宽深比为1∶1 的渠道增温率高0.058 ℃，经10 km可高0.58 ℃，高出123.4%；当渠道走向均为东西走向时，渠道宽深比为2∶1 时增温率为0.141 ℃/km，1.5∶1 时为0.122 ℃/km，1∶1 时为0.099 ℃/km，宽深比为2∶1 的渠道同样条件下比宽深比为1∶1 的渠道增温率高0.042 ℃，经10 km 可高0.42 ℃，高出42.42%。

当渠道宽深比相同，走向不同时，比较不同走向对灌溉水自然增温效果的影响。仍以上午09:00为例，当渠道宽深比为2∶1 时，南北走向增温幅度为0.089 ℃/km，与东西成45°夹角时增温幅度为0.105 ℃/km，东西走向时增温幅度为0.141 ℃/km，同样条件下东西走向的渠道比南北走向的渠道增温率高0.052 ℃/km，经10 km 可高0.52 ℃，高出58.45%；当渠道宽深比为1.5∶1 时，南北走向增温幅度为0.061 ℃/km，与东西成45°夹角时增温幅度为0.079 ℃/km，东西走向时增温幅度为0.122 ℃/km，同样条件下东西走向的渠道比南北走向的渠道增温率高0.061 ℃/km，经10 km可高0.61 ℃，高出100%；当渠道宽深比为1∶1 时，南北走向增温幅度为0.025 ℃/km，与东西成 45°夹角时增温幅度为0.047 ℃/km，东西走向时增温幅度为0.099 ℃/km，同样条件下东西走向的渠道比南北走向的渠道增温率高0.074 ℃/km，经10 km可高0.74 ℃，高出296%。

3 讨 论

热通量计算公式常被用来计算水体的增温[27-28]，但考虑到渠道比较狭窄，水面并不开阔，由于太阳高度角的存在，渠道的尺寸和走向都将会影响灌溉水的增温效果。因此本文对水面的受光面积做了修正，建立了适用于渠道水增温的计算模型。试验结果表明模型的计算结果和实测结果较为符合。此外，李根[29]运用SEBAL 模型和SEBS 模型对南方典型低丘农业小流域的水热通量进行了计算，模型的总体精度与本文模拟精度相当；许多学者[30,32]利用热通量板校正法估算土气界面的水热传输，发现估算结果与真实值存在一定偏差，但可以准确得到热通量变化的相位和方向；孙树臣[33]利用水量平衡过程计算得到的蒸发量大于实测值，分析原因可能是此模型忽略了土壤的深层渗透，而在本文中不存在土壤深层渗透的问题，蒸发量只与风函数、水气温差和靠水面的空气饱和蒸发压力有关，使用模型的蒸发量的计算结果比较接近事实。综上所述，本文使用的热通量模型的计算结果比较可靠，但也存在一定的误差，原因可能主要有以下几点：①物理实验模型为简化的模型，未进行原型观测；②气象条件进行了平均化处理；③装置周围泡沫不能完全避免水固热交换。

模型的计算结果显示灌溉渠道的宽深比越大，灌溉水的增温效果越明显。在本试验模型中，其他条件相同的情况下，宽深比为2∶1 的渠道的增温效率比1∶1 的渠道高42.42%～256%，这与已有的研究结果[6,18-19,34]一致。例如，闫海等[19]也发现渠道增温与渠道的宽深比有关，在他的观察模型中渠道宽深比为5∶1 时平均可增温2.53 ℃/100 m，宽深比为3∶1时平均增温1.71 ℃/100 m。宽深比大的渠道增温效果更好的原因是由于太阳高度角的存在，宽浅式渠道更有利于增加受光面积，从而吸收更多的太阳辐射，达到更好的增温效果。

模型的计算结果显示渠道走向越接近于东西走向，灌溉水的增温效果越明显。在本试验模型中，其他条件相同的情况下，东西走向的渠道增温效率比南北走向的渠道高58.45%～296%。但目前的渠道设计规范中暂未考虑走向这一因素，也鲜有灌溉渠道走向对灌溉水增温效果的影响这方面的研究，但有关于渠道走向对渠床增温效果的类似的研究，例如叶尔肯·巴合提汉[35]和程满金等[36]通过计算证实渠道走向对渠道的日照强度有重要的影响；郭殿祥等[37]通过对渠道接收辐射的计算，发现东西走向的渠道比南北走向的渠道增温效果更佳。本文也只对灌溉渠道走向对灌溉水增温效果的影响做了初步的探究，之后需要附加上遮荫系数综合考虑渠道走向对灌溉水增温的影响。在实际应用中，应根据农作物种类（所需水温不同）、地形及经济因素合理布置渠道的走向，可根据实际情况通过上述模型进行计算来分段布置渠道走向，最大限度的利用自然增温的效果。

4 结 论

1）在热通量公式和水体增温公式的基础上，考虑了太阳高度角、渠道宽深比和渠道走向对水面接收太阳辐射面积的影响，建立了适用于渠道输水过程中灌溉水增温的数学模型，使水体增温公式更接近实际。

2）通过水槽试验模拟渠道，水槽的理论温差与测量温差值较为接近，且变化趋势一致，证实计算模型一定的合理性。

3）在其他条件相同的情况下，宽深比越大，渠道的增温效果越好；越接近东西走向的渠道增温效果越好。因此，在可能的情况下，应使渠道走向接近东西方向并增加渠道宽深比。