A spatial decomposition approach for accelerating buffer analysis of vector data

Li Xiaohua(李晓华)， Guo Mingqiang，Qi Xinhong

(*School of Safety Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, P.R.China)(**Guizhou Coal Mine Design Research Institute Co., Ltd, Guiyang 550025, P.R.China)(***School of Geography and Information Engineering, China University of Geosciences, Wuhan 430074, P.R.China)

Abstract

Key words: high performance spatial computing, buffer analysis, parallel computing, load balancing, vector data

0 Introduction

A buffer in geographic information systems (GIS) is defined as the zone around a geometric geographic feature, measured in units of distance or time[1]. Buffer analysis plays an important role in many applications of GIS, such as environmental measurement and management[2,3], human health[4,5], landscape and urban planning[6,7], geographic data processing and representation.

According to the parallel strategies for spatial analysis, existing studies can be classified into 2 categories: the algorithm-oriented parallel strategy and the data-oriented parallel strategy.

The first is the algorithm-oriented parallel strategy, a strategy that generally changes the current spatial algorithms to make full use of the parallel computing framework to achieve better parallel performance[8-10]. Some researchers proposed a parallel buffer algorithm based on area merging and message passing interface (MPI) to improve the performance of buffer analysis on processing large datasets. A visualization-oriented buffer analysis method which was developed based on a fully optimized hybrid-parallel processing architecture was proposed by Ma et al.[11], they put forward an efficient spatial-index-based buffer generation method to generate the results.

The second category is the data-oriented parallel strategy, which mainly focuses on data partition and data organization to suit the corresponding parallel framework.Some researchers developed a distributed spatial index based on Apache Storm, which is an open-source distributed real-time computation system[12]. There are many great improvements in spatial index and data skew in Hadoop. A cluster-computing-oriented parallel vector buffer generating algorithm was proposed by Shen et al.[13], which contains a data partition method based on Hilbert space filling curve.

These parallel approaches mentioned above have obtained high performance of spatial operations. However, the improvement of each existing algorithm is a very complex work, and it requires vast redevelopment. In order to address the problem, a spatial decomposition approach for vector buffer analysis is proposed.

The rest of the paper is organized in the following. Section 1 articulates the spatial decomposition approach. Section 2 presents a series of experiments to demonstrate the effectiveness and performance of the new approach proposed by this paper. Conclusion and future work are given in Section 3.

1 Methods

1.1 Construction of computational intensity model

The relationship between the computing time and the number of a feature’s vertices for the retrieve, buffer and write steps of polyline and polygon buffer analysis can be represented by linear model[14,15]. Thus, these models can be used to generate the computational intensity transform functions (CITFs), so as to estimate the computational intensity of generating a group of polyline and polygon buffer analysis results. First, the sub-CITFs of the single polygon or polyline feature can be built, as shown in Eq.(1) and Eq.(2).

CL(x)=(a1+a2+a3)x+(b1+b2+b3)

(1)

CP(x)=(a4+a5+a6)x+(b4+b5+b6)

(2)

where,CL,CPare the computing time of the polyline and polygon buffer analysis respectively;xis the number of vertices of a polyline or a polygon feature;a1,a2,a3,a4,a5,a6are the slope of the functions of 3 steps respectively; andb1,b2,b3,b4,b5,b6are the intercept respectively.

Then the overall CITFs can be constructed for a group of polylines and polygons.

(3)

(4)

where,WLis the overall computing time for a group of polylines,WPis the overall computing time for a group of polygons,nis the number of polylines or polygons,xiis the number of vertices of the polyline or polygon featurei.

The CITFs can be used to estimate the computational intensity of generating buffers for a group of polylines or polygons. It is significant for the spatial representation of buffer analysis computational intensity.

1.2 Spatial representation of computational intensity

In order to ensure the effectiveness of the parallel scheduling method, the spatial distribution of computational intensity of buffer generation must be properly represented. In this research, the computational intensity surface (CIS) approach proposed by Wang et al.[15]is exploited to solve this issue. The spatial computational domain of a vector layer is divided into a group of regular lattices so that a computational intensity grid (CIG) for buffer analysis can be generated. A 4×4 CIG of polygon dataset is shown in Fig.1, whereWijis the computational intensity of the lattice at rowiand columnjin the grid.Wijcan be calculated by Eq.(3) and Eq.(4) for polylines and polygons respectively.

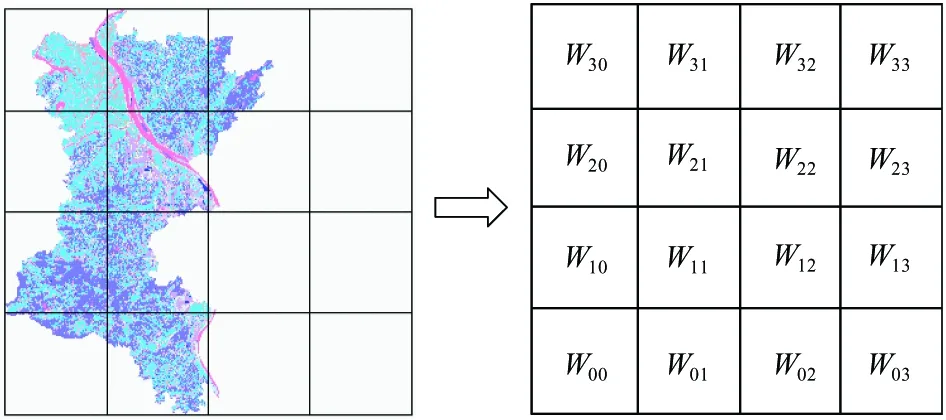
Fig.1 A 4×4 CIG for the polygon buffer analysis

1.3 Spatial decomposition for parallel buffer analysis

The ideal decomposition for parallel buffer analysis is to ensure that every task has similar computational intensity, so that all the parallel tasks can be completed simultaneously.However, regular decomposition strategies only pay attention to decomposing sub-domains evenly in areas.Vertical decomposition(VD) method divides the whole domain to equally sized column-like sub-domains (Fig.2(a)), while horizontal decomposition(HD) generates equally sized row-like sub-domains (Fig.2(b)). And the vertical and horizontal decomposition (VHD) generates the block-like sub-domains by both columns and rows (Fig.2(c)). These regular decomposition methods do not take the spatial distribution of the features in the dataset into consideration,and just decompose the computational domain to sub-domains evenly in areas. If the features are not homogeneous in space, the regular decomposition methods may result in great load imbalance among sub domains. Therefore, the spatial decomposition strategy based on computational intensity is proposed to address the problem.

Fig.2 Three regular decomposition methods

The spatial decomposition (SD) method is based on HD or VD method. This approach can effectively divide spatial computational domain into sub-domains with same computational intensity. As shown in Fig.3, after CIG is formed, the sum (W0,W1,W2,W3) of the computational intensity of the lattices is firstly computed for each row.Wtotalcan be calculated as the overall computational intensity, andWtaskcan be calculated as the computational intensity of each sub task. Then, the computational intensity grid needs to be scanned row by row, the computational intensity of each row should be compared withWtask. All of the rows will be scanned and all sub-domains with same computational intensity will be generated.

Fig.3 The workflow of the SD method

2 Experiments

2.1 Experimental environment and dataset description

In order to evaluate the performance of the proposed method, a group of experiments are conducted in the parallel buffer analysis framework on QGIS platforms. SD is compared with regular decomposition methods. The computing nodes are composed of 2 Intel Xeon E5620 8-core CPUs at 2.4 GHz and 16 GB of memory. And the experiments are conducted by QGIS SDK 3.4.8.

Aiming to demonstrate the availability and efficiency of proposed SD methods, 2 real-world vector datasets are adopted in the experiments (Table 1). Dataset A and dataset B present the same geographic objects with different feature type.

Table 1 Description of vector dataset

2.2 Experiments and performance assessments

Firstly, the API of QGIS is selected to conduct the parallel buffer analysis task with varying numbers of threads. The sub-domains of parallel buffer analysis task are generated by VD, HD and SD respectively. The VD and HD methods divided the computational domain by area.These methods can be easily realized, but they will lead to great load imbalance. In this work, 32×32 CIGs are used to conduct a group of experiments. Three various 8 sub-domains decomposition results of dataset A and dataset B are shown in Fig.4 and Fig.5. The decomposition results of VD and HD are uneven in computational intensity, while the computing load of sub-domains generated by SD is almost equal.

Fig.4 Three types of decomposition for dataset A

Fig.5 Three types of decomposition for dataset B

A serial buffer analysis program using dataset A and dataset B is conducted to offer the benchmark for assessing the performance of the parallel program. The computing time of serial buffer analysis of dataset A is 23 076.335 ms, and that of dataset B is 50 272.347 ms. A set of experiments are carried out by using the parallel buffer analysis program with various numbers of threads (2-8). As shown in Fig.6, the computing time decreases with the increasing number of threads, and SD achieves the best performance. Fig.7 shows that SD achieves near-linear speedups on dataset A and dataset B, and the speedups are greatly higher than that of VD and HD methods. The reason of near-linear speedups of SD is that the spatial distribution of computational intensity is taken into consideration. The new approach ensures that the workload is averagely assigned to parallel computing nodes.

Fig.6 Computing times of 3 decomposition methods

Fig.7 Speed-ups of 3 decomposition methods

3 Conclusion

With the growing volume of spatial data, existing vector buffer analysis algorithms cannot meet the demands of fast data processing. In this work, a spatial decomposition for vector buffer analysis based on spatial computational intensity is proposed, so as to generate balancing sub-domains in parallel environment.

With the relationship between the number of vertices and the buffer analysis computing time, the CITFs are generated to estimate the computational intensity. Based on the CITFs, CIGs of polyline and polygon are constructed to represent the spatial distribution of computational intensity for buffer analysis. The computational domain can be effectively divided by the spatial decomposition approach developed in this work.

Future work will focus on how to partition the vector features distributed in the adjacent area of 2 sub-domains, so as to further address the balance partition problem for vector data spatial analysis.