Grouping pilot allocation scheme based on matching algorithm in massive MIMO system
Xu Lei(徐 磊), Wang Zhaorui, Yao Yijing, Zhao Xinying, Fang Hongyu, Li Xiaohui
(School of Electronics and Information Engineering, Anhui University, Hefei 230039, P.R.China)
Abstract
Key words: the sum rates of system, pilot allocation, user grouping, matching algorithm, low complexity
0 Introduction
Massive multiple-input multiple-output (MIMO) technology has been recently become a hot topic of wireless communication[1,2]. In massive MIMO system, each base station (BS) is equipped with a large number of antennas, which are usually much larger than the number of active users[3]. The feedback amount of channel state information (CSI) is increased by increasing the number of antennas, and the time required for feedback is much larger than the channel coherence time. The present large-scale MIMO system is mainly working on time division duplex (TDD) mode, so the base station obtains the uplink CSI according to the channel estimation of the user’s uplink pilot, and can obtain the downlink CSI according to the reciprocity of time division duplex. Because the number of orthogonal pilots provided by the system is limited, the same pilot sequence is usually reused in adjacent cells, which is called pilot pollution (pilot contamination, PC)[4]. The research results show that, when pilot pollution exists, with the increase of the number of base station antennas, the incoherent interference such as noise can be gradually eliminated, and the capacity of the system will not continue to increase when the capacity of the system increases to a certain extent. The user coherent interference caused by pilot pollution has become the main bottleneck limiting the performance of massive MIMO system[5]. Therefore, it is of great significance to study how to reduce pilot pollution in massive MIMO system.
In recent years, the pilot pollution problem has been investigated widely. Among them, the pilot allocation scheme, which is one of the key solutions, has made some progress. A pilot allocation scheme based on alliance game was proposed in Ref.[6], which can effectively mitigate the pilot pollution of the system, but also brings high computational complexity. The pilot allocation scheme based on user geographic location information mitigates pilot pollution effectively[7], but it requires complex and accurate detection of the arrival angle of user signal. Ref.[8] proposed a smart pilot allocation scheme based on the minimum-maximum matching principle. The scheme maximizes the SINR of edge users by assigning pilots with lower inter-cell interference to users with poor channel quality in the cell, but the system capacity has not been significantly improved due to the limitations of the algorithm. The principal finding of Ref.[9] is that, a scheme which is based on complex downlink and uplink training procedures can mitigate pilot pollution. Combining the number of pilots and users, a traditional Hungarian algorithm pilot allocation scheme was proposed in Ref.[10]. The Hungarian algorithm is used to allocate the pilot sequences, which improves the user sum rates and reduces the mean square error. Ref.[11] proposed a pilot allocation scheme based on weighted graph coloring to mitigate pilot pollution in multi-cell system. In Ref.[12], combining with the current discrete Fourier transform filter channel estimation technique, a pilot allocation algorithm based on vertex graph coloring was proposed to mitigate inter-cell interference. A novel pilot allocation scheme optimizes uplink performance using the maximum-minimum fairness problem to mitigate pilot pollution in multi-cell system[13]. A smart strategy of maximizing the average receive power is adopted to delete spurious solutions and preserve the true optimal solution by linear searching over a set of limited finite candidate directions, and it achieves the hybrid CRLB with low complexity in Ref.[14]. Ref.[15] proposed a heuristic algorithm to mitigate the influence of pilot pollution by optimizing the pilot allocation of shared resources between base stations. An approximate optimal solution algorithm was proposed, and the scheme combines the harmonic SINR effect function to mitigate pilot pollution and improve system performance in Ref.[16]. Ref.[17] mitigates pilot pollution by learning more about the relationship between pilot allocation and users. However, the above scheme ignores the difference in anti-interference ability between users, and the pilots are allocated to users in the cell in the same manner. A pilot allocation scheme based on user grouping was proposed in Ref.[18], the users are grouped according to the difference of the anti-interference ability of the target cell users and it distributes the pilots in different ways. It verifies the relationship between pilot frequency and pilot pollution and guarantees the fairness of weak users, but the system performance is not significantly improved. Motivated by Ref.[19], we wonder whether the users can be grouped and use different matching scheme to assign pilots.
This paper proposes a grouping pilot allocation scheme with matching algorithm, which is designed based on the difference among the anti-interference ability of different users, combined with the efficient and simple advantages of the Hungarian algorithm in calculating the maximum matching value problem and the low complexity advantage of the minimum-maximum matching method. Firstly, according to the large-scale fading coefficient of the target cell users, the users are divided into strong user group and the weak user group. Then, the channel quality of the users and the pilot interference intensity of the users in the adjacent cell are detected. Finally, in order to improve the sum rates of system, the strong users adopt the Hungarian algorithm for pilot allocation to improve the uplink achievable sum rates, and the weak users utilize the minimum-maximum matching method for pilot allocation to ensure the QoS requirements.
The symbols used are defined as follows:IMdenotes theM-order identity matrix. (·)T, (·)Hand E(·) denote the transpose, conjugate transpose, and average of the matrix respectively.
1 System model
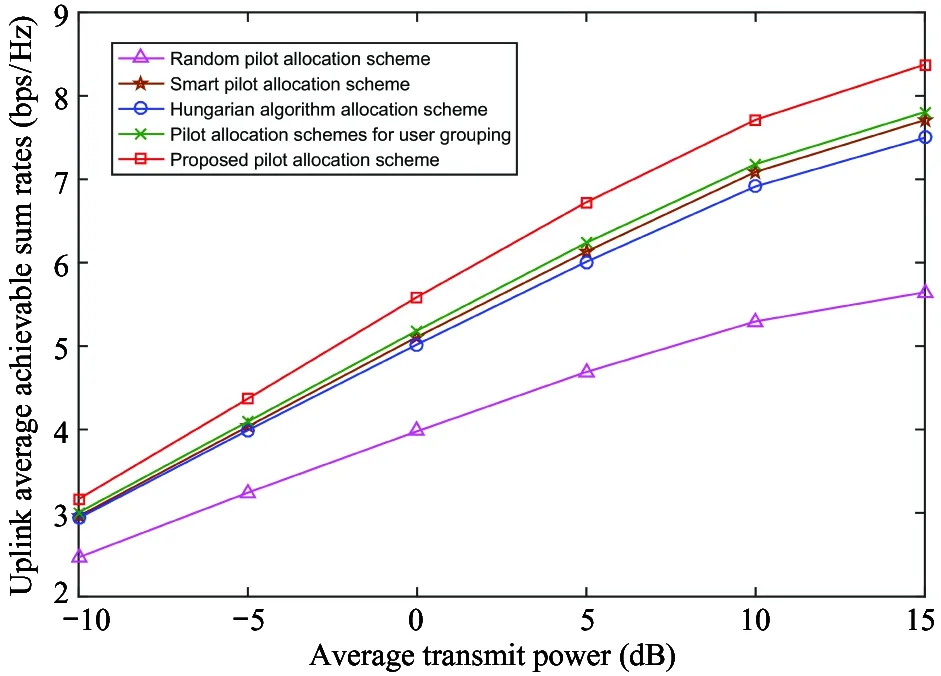
This paper considers a massive MIMO system composed ofLhexagonal cells, and each cell containsK(K< Fig.1 Massive MIMO system model Supposing the system works in TDD mode, the channel vector from thek-th user in thej-th cell to the BS in thei-th cell can be modeled as (1) where,g〈j, k〉i~CN(0,IM) denotes the small-scale fading vectors from thek-th user in thej-th cell to the BS in thei-th cell,β〈j, k〉, idenotes the large-scale fading coefficient. Since geometry fading and shadow fading change slowly in space the index relative to the frequency and the base station antenna is constant, soβ〈j, k〉, ican be expressed as (2) where,z〈j, k〉, irepresents the shadow fading,αis the path loss exponent,Ris the cell radius andr〈j, k〉, idenotes the distance from thek-th user in thej-th cell to the BS in thei-th cell. Assuming that there are a total ofSavailable pilot sequences, andS≥K, the pilot sequencesΦ=[φ1φ2…φS]T∈CS×τisS×τorthogonal matrix,τis the length of the pilot training sequence sent by the user andΦΦH=IS. Supposing each user sends pilot sequence to the BS in the same cell, and the transmit power of each pilot is the same, the received pilot signal at the BS in thei-th cell can be represented as (3) where,ρpdenotes uplink pilot transmit power, andNi~CN(0,1) denotes the additive Gaussian white noise (AWGN) matrix with mean 0 and variance 1. The received user data at the BS in thei-th cell can be represented as (4) where,ρudenotes the uplink data transmission power,x〈j, k〉denotes the data symbol from thek-th user in thej-th cell,nidenotes the AWGN. After receiving the pilot sequenceφk, the result of the channel estimate for thek-th user in thei-th cell based on can be represented as (5) (6) (7) When the number of antennas tends to infinity, (8) The uplink average achievable sum rates of users ini-th cell can be calculated as (9) The large-scale fading coefficients of users in the target cell are detected and sorted in descending order. The users are divided into strong user group and weak user group equally according to the user number, which are denoted byUsandUwrespectively. The users in strong user group have better channel quality, which are less affected by pilot pollution, so the pilot sequences with larger pollution are allocated to the strong users to improve the system sum rates. While the user in the weak user group has poor channel quality, which are greatly affected by pilot pollution, so the pilot sequences with less pollution are allocated to the weak users, and the minimum-maximum matching method is adopted to ensure the QoS of weak user. When the number of the BS antennas tends to infinity, Eq.(8) shows that the uplink SINR of thek-th user in thei-th cell is mainly related to the large-scale fading coefficientβ〈i, k〉i. Furthermore, the large-scale fading coefficient changes slowly, so it is easy to be tracked by the BS. Therefore, the pilot allocation problem for strong users can be modeled as follows: (10) Since the pilots in the system are orthogonal mutually, each pilot uses the same transmit power, and the relationship between the number of pilot and the number of users isS≥K, so the essence of the pilot allocation problem is one-to-one matching problem between the user and the pilot. Therefore, the pilot allocation problem of strong user group can be transformed to a maximum matching problem, which let the uplink SINR of the strong users be as the objective function. So the basic principle of Hungarian algorithm is introduced at first. (1) The basic principle of Hungarian algorithm The Hungarian algorithm is a maximum matching algorithm for finding bipartite graphs with augmented paths[20]. The so-called bipartite graph is a special model in graph theory. In Fig.2(a), letG=(V,E) be a undirected graph. If the vertex setVcan be divided into two disjoint subsetsV1andV2, and the two vertices of each line in the graph belong toV1andV2respectively,Gis called a bipartite graph. If there are no common vertices among the lines inG, the matching set consisting of these lines isE, and in which the maximum matching setAcontains the maximum number of the lines. The two vertices of each line are called matching points, and the two vertices are one-to-one matching. e.g., the number 3 in setV1and the number 4 in setV2are one-to-one matching. The maximum matching number in Fig.2(a) is 4, it has two maximum matching schemes and one of the maximum matching schemes is shown in Fig.2(b). Similarly, although the result of pilot allocation in strong user group is the maximum matching, the set with the maximum matching number may have multiple results, and further selection criteria need to be made. Fig.2 Bipartite graph structure (2) Pilot allocation with Hungarian algorithm (11) In order to achieve the maximum uplink SINR of the strong users, the above problem Eq.(10) can be solved by searching the maximum value of element summation in matrix Eq.(11), i.e.,Kelements are selected in the matrix, and one element is selected for per row and per column. So the maximum matching setAwith the maximum algebraic summation of theKelements can be determined, wheresrepresents thes-th pilot. The minimum-maximum matching method[8]is adopted in weak user group to allocate pilots according to the pilot pollution intensity. The pilot with less pollution is allocated to the user with the worst channel quality, thereby the uplink achievable sum rates of the weak users can be improved. The pilot allocation for the weak users can be modeled as follows: (12) The specific steps of grouping pilot allocation scheme based on matching algorithm are as follows: (1) Detecting the large-scale fading coefficient of the target cell user and arranging them in ascending order. According to the number of users, users are equally divided into strong user groupUsand weak user groupUw. (2) The pilots are sorted in ascending order according to the interference intensity generated by the target cell. Select the firstKpilots and save them inφ1, whereKis an even number. And whenKis an odd number, select the firstK+1 pilots and save them inφ1. (3) The latterK/2 or (K+1)/2 pilots inφ1are allocated toUsby Hungarian algorithm. (4) The residualK/2 or (K-1)/2 pilots are allocated toUwby minimum-maximum matching method. (5) Finally, the result of pilot allocation in the target cell user is obtained. The users in the target cell are allocated according to the proposed method, and the users in the adjacent cell are allocated by the random pilot allocation scheme. Monte Carlo method is used for system simulation, and assuming that the distance from base station in target cell to the adjacent cell isr=1.2R. The specific simulation parameters are shown in Table 1. Table 1 Simulation parameters In the case withM=128, the cumulative distribution function (CDF) curve of the minimum uplink SINR of the weak users in the proposed scheme and that of in the random allocation scheme are shown in Fig.3. Compared with random allocation scheme, the minimum uplink SINR of the proposed scheme increases by about 10 dB. Because the weak users adopt the minimum-maximum matching method, the advantages of the smart pilot allocation scheme and the grouping pilot allocation scheme are maintained, that is the proposed scheme can guarantee the QoS of the weak users. Fig.3 The CDF of the minimum SINR of the weak users The CDF curves of the average uplink SINR for users in the target cell are shown in Fig.4. Obviously, the average uplink SINR of the target cell users can be effectively improved by increasing the number of base station antennas. When the number of base station antennas increases fromM=32 toM=128, the performance of all pilot allocation scheme is improved by approximately 5 dB. In the case withM=128 andCDF=0.5, compared with pilot allocation scheme based on user grouping, Hungarian algorithm allocation scheme and smart pilot allocation scheme, the uplink average SINR of proposed scheme increases by about 1.7 dB, 2 dB and 1.8 dB respectively. Fig.4 The CDF of uplink average SINR Fig.5 illustrates the trends of the uplink achievable sum rates changing with the number of base station antennas. It shows that the uplink achievable sum rates increase with the increase of the number of base station antennas. Obviously, the uplink achievable sum rates can be effectively improved by increasing the number of base station antennas. Because the minimum uplink SINR achievable sum rate of the proposed scheme is superior to that of the other 3 schemes, the achievable sum rate can be increased by up to about 1 dB. Fig.5 The trends of the uplink achievable sum rates changing Fig.6 shows, in the case withM=128, the trends of the uplink achievable sum rates changing with the uplink transmit power. Obviously, the uplink achievable sum rates can be effectively improved by increasing with the uplink transmit power. Compared to pilot allocation scheme based on user grouping, Hungarian algorithm allocation scheme, smart pilot allocation scheme and random pilot allocation scheme, the uplink achievable sum rate of the proposed scheme is better than that of the other 4 pilot allocation schemes, and is improved by 0.52 bps/Hz, 0.62 bps/Hz, 0.8 bps/Hz and 3 bps/Hz respectively. When the transmit power increases to a certain degree, the uplink average achievable sum rates tend to be saturated. Fig.6 The trends of the uplink achievable sum rates changing A grouping pilot allocation scheme based on matching algorithm is proposed in this paper, which fully considers the difference of the anti-interference ability between users. The strong users adopted the Hungarian algorithm for pilot allocation. Considering Hungarian algorithm may obtain multiple matching results, the optimal matching result is selected by using the variance to ensure the fairness of strong users. The weak users adopt the minimum-maximum matching method to perform pilot allocation according to the pilot pollution intensity. Compared with different pilot allocation schemes, the time complexity of the proposed algorithm is acceptable, and the proposed pilot allocation scheme can effectively improve the system performance.

2 Grouping pilot allocation scheme based on matching algorithm
2.1 User grouping
2.2 Pilot allocation in strong user group

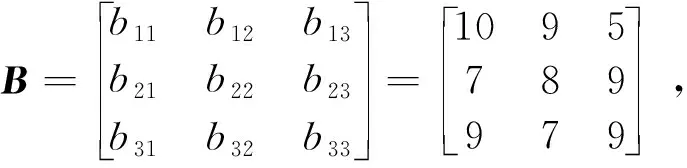
2.3 Pilot allocation in weak group
3 The algorithm flow of pilot allocation scheme
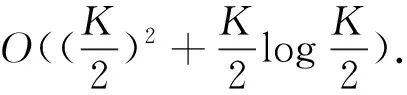
4 Simulation results and analysis




5 Conclusion
 High Technology Letters2020年4期
High Technology Letters2020年4期
- High Technology Letters的其它文章
- Experimental study on vibration suppression in a rotor system under base excitation using an integral squeeze film damper
- Fraudulent phone call recognition method based on convolutional neural network
- Behavior recognition based on the fusion of 3D-BN-VGG and LSTM network
- Dynamic A* path finding algorithm and 3D lidar based obstacle avoidance strategy for autonomous vehicles
- An effective indoor radio map construction scheme based on crowdsourced samples
- Optimal UAV deployment in downlink non-orthogonal multiple access system: a two-user case
