MoS2中带电点缺陷性能的理论研究

（湖南工业大学 理学院，湖南 株洲 412007）

1 研究背景

二维（2D）半导体材料因具有独特的物理化学性质，是未来电子学和光电子学材料的有力候选者[1-8]。但是，通过杂质或缺陷的引入使材料在工作温度下产生足够多的自由载流子是半导体器件材料的重要先决条件之一。因此，二维半导体材料能否作为电子和光电器件材料的关键取决于其掺杂性能[1-4]，这就要求从根本上了解其掺杂和缺陷的性质。

可掺杂性（为了在工作温度下显著产生超过一定浓度的载流子而引入的缺陷或杂质）是半导体材料在电子器件和光电器件中应用的关键。在物理学上，用缺陷离化能（ionized energy，IE）表示材料的掺杂性能特征。离化能是一个缺陷或者杂质释放电子或者产生空穴所需要的能量。带电缺陷的离化能可以通过分析材料的吸收谱、温度依赖的电导率等实验数据获得[9-10]，也可以直接通过理论计算获得。即通过构建超原胞，在周期性边界条件下基于密度泛函理论计算，可以获得杂质的离化能。在过去的20 多年里，第一性原理计算已经被广泛地应用于掺杂体系中杂质离化能的预测。

传统方法中常采用凝胶模型（jellium model，JM）计算带电缺陷体系。在JM 里，一个超原胞里包含一个带电的缺陷。通过减少（增加）体系的电子数目来模拟这个缺陷释放（捕获）电子。为了保证计算体系的电中性，即核电数目与电子数目相等，以及消除由于周期性边界条件引起的静电势能，在计算过程中加入了一个均匀的背景电荷[11]。基于这种计算方法上的一些基本理论概念还有一些争议[12]，主要有以下两个方面。

1）电离电子（空穴）所处的状态不真实。在JM中，可以将自由载流子产生的物理过程看成是缺陷上的电子电离后位于一个均匀的平面波状的虚拟态上（或者是一个均匀的平面波状的虚拟态上的电子被缺陷捕获），这个态称之为jellium 态。jellium 态的能量为统计平均的能量Ef，其计算原理如图1a所示。从宏观统计的角度看，可以将Ef看成是电子占据导带（价带中空穴）的平均能量。电子占据导带（价带中空穴）的分布是满足狄拉克费米分布的，其分布函数为，式中，E为电子的能量，KB为玻尔兹曼常数，T为温度。这个非局域的jellium 态电荷能够很好地近似于无缺陷体系（host）下的带边的态（最高占据态和最低未占据态），尤其是能带带边有s 电子或p 电子构成的传统半导体体系[13-15]。因此，JM 模型具有一定的合理性，尤其是一些与缺陷离化能相关的宏观统计量，比如载流子的浓度、电导率等。然而，在微观视角下，一个从缺陷态激发后的电子或空穴应该处在一个真实的态上，而不是一个虚拟的态上。

2）人为引入了长程库伦相互作用使得计算结果发散，尤其是在低维度体系中。传统的JM 模型在处理低维度体系时，还存在一个巨大的挑战。在第一性原理计算的过程中，通常采用在周期性边界条件下加入真空层的方式来模拟低维体系。这使得在使用JM模型处理带电缺陷体系时，对电荷中心的屏蔽效应减弱，尤其是在含有真空层的方向上。在周期性边界条件下，带电缺陷与其镜像之间存在长程的库伦相互作用[11-12,16]，这使得用JM 模型计算得到的带电缺陷形成能是一个发散的结果（形成能与真空层的厚度成正比例变化）。更重要的是，在三维半导体材料中，均匀的Jellium 电荷分布，能够非常好地近似替代能带边缘的态，但是在低维材料中却存在严重的错误。在三维材料中，材料本身是填充整个三维空间的。而对于低维材料的计算，因周期性边界条件在计算体系中人为引入了真空层，导致使用均匀的jellium 电荷分布时就无法避免地把电荷填充到真空当中，如图1a所示。而真实的host 带边的态只会分布在低维材料内，不会处于人为加入的真空层中。

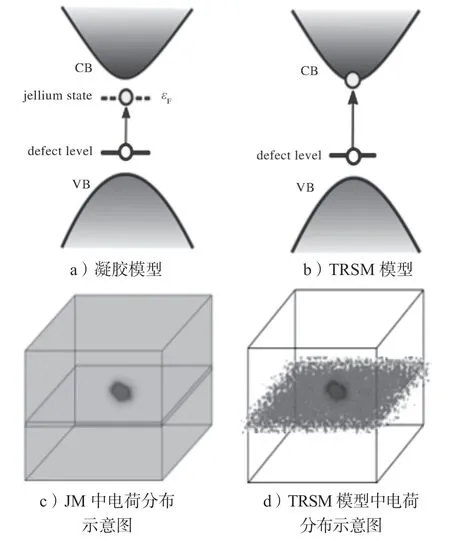
图1 带电缺陷计算原理图Fig.1 Schematic diagram of charged defect calculation

过去的数年中，研究者们提出了各种修正的方案来努力克服这一问题。这些方案包括人为地把背景电荷局域到固定区域[17-21]，或者加入一些后处理进行修正[22-31]。例如N.A.Richter 等[17]通过赝原子掺杂[20]的方式模拟了MgO 表面O 原子空位缺陷的电离情况。赝原子掺杂，是通过修改计算超胞里Mg 原子的核电子数目来实现背景电荷的。基于JM 模型，H.P.Komsa 等[32]提出了加入静电势能修正项来研究带电表面和界面，进而推广到二维体系[33]。这额外的静电势能来源于两部分[22]：一部分是带电缺陷与其镜像之间的势能；另一部分是带电缺陷与所加入的背景电荷之间的势能。聚焦于如何精确计算这额外的静电势能[24-27,33]或者加入后处理手段来修正离化能[28,34]，人们提出了一些应用于低维体系的缺陷计算方案。然而这些修正方法对于自由载流子的状态描述在物理上仍然不够严谨。最近Xiao J.等[35]提出了一个严格的、透明的、统一的带电缺陷计算方法——TRSM（transplant real state method）模型。在TRSM模型中，host 的带边态（导带底和价带顶）直接被移植到所要计算的缺陷体系中，并且电离的载流子放到了被移植进来的host 的态上。这样就成功模拟了真实情况下缺陷上载流子电离的过程，如图1b所示。这种方法保证了计算体系的电中性，因此不需要加入补偿性的背景电荷。对于块体体系，计算所得到的结果几乎与JM 模型计算的结果重合。对于低维体系，这种方法自然地屏蔽了缺陷上的电荷，从而避免了因长程库伦相互作用带来的计算偏差。更重要的是，整个计算过程透明而简单。TRSM 方法可以被应用于带电缺陷所有维度的系统中，例如块体材料、2D材料、量子点、纳米线、表面和界面等。

以MoS2为代表的、层状的二硫化过渡金属元素化合物，在实验上已经被成功制备[36-37]，由于这类材料具有独特的物理性质，使得它们极有可能在未来被应用于电子器件、光电材料等领域中[2,36-37]。且近10 a 来，MoS2一直是二维半导体材料领域研究的热点之一[38-46]。单层MoS2是直接带隙的半导体，其能隙大小约为1.9 eV[38,43]。在实验测量中发现，由单层MoS2构成的晶体管，其电子在室温下的迁移率至少有200 cm2V-1s-1，室温下的电流开关比达1×108[36]。在单层MoS2中，存在两种不同的子格：Mo 原子和两个S 原子。由于结构上空间反演对称的破缺，在布里渊区的高对称点——K点，会出现因自旋轨道耦合效应而引起的能带劈裂。理论研究和实验研究都发现，价带在K点的自旋轨道耦合引起的自旋劈裂能隙超过了100 meV（理论计算数值约为150 meV[42,44]，实验中测得的数值约为160 meV[45-46]）。利用这个性质，在单层MoS2中，可以使用极化光光致发光技术以实现谷电子的极化[45-46]。

MoS2作为新型的半导体电子器件材料，如何调控其载流子特性是研究者们关注的核心问题。本文拟基于TRSM 模型，研究MoS2材料中本征点缺陷的形成能。计算结果表明，对于空位缺陷（S空位、Mo空位）、替代缺陷（Mo 替代S 和S 替代Mo），以及本征原子吸附（S、Mo 原子吸附）都不能有效地产生载流子。但是H 原子的吸附能够提供电子载流子，这可能是实验中测得MoS2材料成n 型半导体的原因。

2 理论方法

2.1 第一性原理计算的方法与参数

本文计算采用的程序包为QE（quantum-espresso package）[47-48]，交换关联势采用的是GGA-PBE（generalized gradient approximation—J.P.Perdew，K.Burke，M.Ernzerhof）[49]。整个计算中只选取了Γ点来代表整个布里渊区。对于价电子采用的是模守恒赝势[50-51]。平面波基组的动能截断能设定为1.417×10-16J。在该截断能设定下，体系的能量和带隙大小达到了收敛值。计算时，能量的收敛标准为2.180×10-30J。原子结构都通过了充分的弛豫，收敛标准为每个原子上的残余力小于4.119×10-18J/m。本文计算得到的MoS2体系的能隙大小如表1所示。分析表1中的数据可以得知，本文采用的计算参数得到的MoS2体系能隙与文献报道中理论计算的数值基本一致[38,41-43]。由于GGA 交换关联势会低估能隙大小，所以理论计算的数值要比实验数值略低一些。

表1 单层、双层和块体MoS2 的能隙大小Table 1 Energy band gap of monolayer,bilayer and bulk MoS2

2.2 带电缺陷计算理论和计算方法

2.2.1 TRSM 模型介绍

在真实情况中，无论是块体还是低维体系中缺陷中的载流子电离过程都是一样的，那就是缺陷态的载流子被激发到没有受到缺陷扰动的能带边缘态。故所要研究或者构建的应该是一个无限大的超原胞。基于这一事实的启发，课题组提出把host（即不含缺陷的完整体系）的带边态，如导带底或价带顶，移植到所计算的缺陷体系中，同时保证载流子占据这个被移植进来的态。这样就实现了真实的缺陷电离过程，即载流子被激发到host 中的带边。这个过程的示意图如图1b所示。该带电缺陷的方法称为TRSM 模型。在TRSM 模型中，带电缺陷和被激发的载流子都处于同一个超胞中，因而整个计算超胞是电中性的。因为移植进来的是材料本身的一个真实的态，它只会分布在材料本身上，所以在真空区域中不会分布电荷。这样将大大增加对带电缺陷的电荷屏蔽效应，从而消除在低维体系中能量发散的问题。同时，该模型也克服了将密度泛函理论计算方法应用在带电缺陷体系中存在的困难[12]。

2.2.2 TRSM 模型计算的实现

接下来介绍如何实现TRSM 的计算，图2是TRSM 模型中电子自洽计算循环示意图。图中ψd表示缺陷态；ψCBM_bulk和ψVBM_bulk分别表示host 中的导带底和价带顶；λ和fi是与占据数相关的系数。

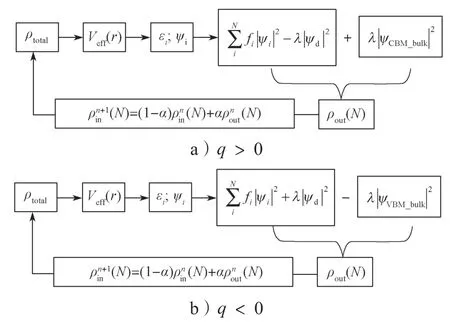
图2 TRSM 模型中的自洽计算流程示意图Fig.2 Schematic diagram of the self-consistent calculation process in the TRSM model

对于缺陷为施主的体系（q＞0），是缺陷态上的电子被激发到host 中的导带底。在缺陷体系中，所有的导带态会受到缺陷的扰动，所以host 导带底这一条态在缺陷体系中并不存在。所以先构建与缺陷体系原胞相同的host 结构，并且把host 中的导带底态波函数输出至硬盘，然后执行TRSM 的计算。在执行TRSM 自洽计算的每一步骤中，host 的导带底态都从硬盘中读入。在计算总的电荷密度分布时，将缺陷态的电荷密度分布减去，再加上host 的导带底态的电荷密度分布，这样即可以实现缺陷态上电子被激发到导带上的这一物理现象。对于q＜0 的情况，则是保存host 的价带顶态，在自洽计算的每一步中读入这个价带顶态，并在总的电荷密度分布计算中减去价带顶态的分布，同时加上缺陷态的电荷密度分布。在B-TRSM 的计算中，每一条带的占据状态预先给定（和C-DFT 的计算相同），在自洽计算的第一步读入host 的导带底态或价带顶态，并计算得到总的电荷密度分布。在后续的自洽计算步骤中则不再读入。在TRSM 中则是每一步骤都读入，并参与总的电荷密度分布计算。

2.2.3 TRSM 模型中带电缺陷形成能的计算

下面介绍修正后的带电缺陷形成能的计算公式。对于施主缺陷（q＞0），带电缺陷形成能是费米能级的函数，可以表示为

式中：q为激发的电子数目；

α为缺陷；

εD为缺陷态能级；

εF为费米能级；

为host 的导带底态。

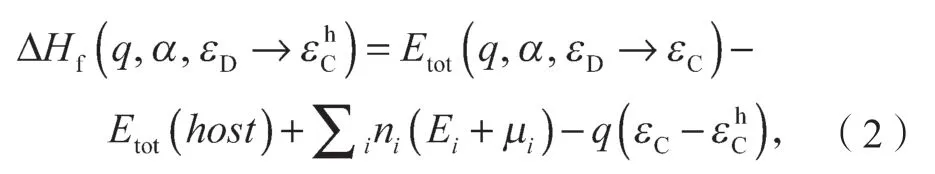
Etot(host)为没有缺陷时体系的总能，其计算用的超原胞大小与有缺陷时计算的超原胞大小相同；

ni为α缺陷下加入或移除的元素的数目；

μi为i组成成分的化学势能，这个势能相对于i组成成分单质块体或气体状态时的能量Ei；

εC-为本征值对齐的修正项。

在进行TRSM 计算时，虽然电子是处于所引入的host 导带底态上，但是计算输出的本征值不一定和host 体系中的本征值一样。所以需要加入本征值对齐的修正。

相类似，对于受主缺陷（q＜0），带电缺陷形成能可以表示为

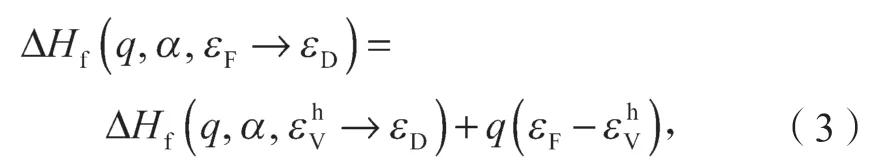
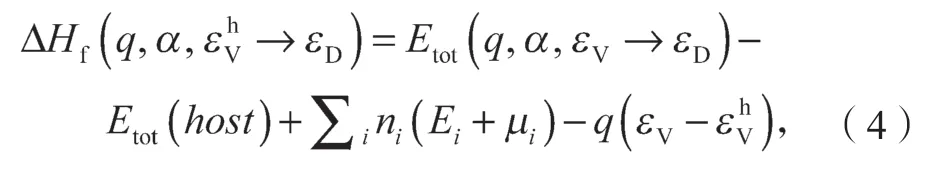
在同一个缺陷下两个不同带电状态（q和q'）之间的转化能级εα(q/q')是这两个带电状态形成能相同时对应的费米能级。根据式（1），可以得到施主缺陷下相对于价带顶的转化能级如下：

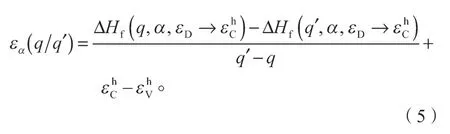
对于受主缺陷情况下的转换能级为

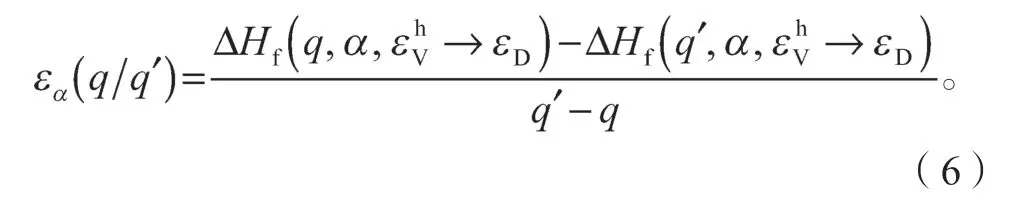
JM 模型下计算电缺陷形成能的公式可以参考相关文献[34]。

3 计算结果与讨论

3.1 原胞大小和真空层对计算结果的影响

首先，采用JM 和TRSM 两种模型，计算单层MoS2中单S 空位两种带电缺陷（表示单S 空位提供2 个自由电子；表示单S 空位吸附2 个自由电子）形成能ΔHf与计算超胞之间的关系，所得结果如图3所示，所有的计算基于以下条件：μi=εF=εV=0 eV。

从图3a中可以明显看到，JM 模型计算所得的形成能与真空层厚度Lz的大小成正比例关系。这是由于在JM 模型里，补偿的背景电荷填充到了真空层中，导致背景电荷对缺陷带电中心的电荷屏蔽效应较差，从而多出了长程的库伦相互作用能[34]。而TRSM 模型计算结果所得形成能与Lz的大小无关。图3b是带电缺陷形成能与计算体系横截面S（超胞大小）的关系曲线，观察曲线可以看到，随着超胞的增大，带电缺陷形成能会逐渐趋于一个收敛的数值。在收敛速度上，TRSM 模型与JM 模型相当。在TRSM 模型中，当超胞大于6×6 倍原胞时，ΔHf基本收敛，因此后续的计算中采用的超胞大小都为6×6 倍原胞，Lz为20×10-10m。

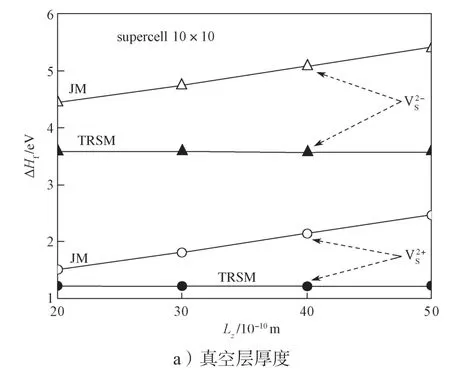
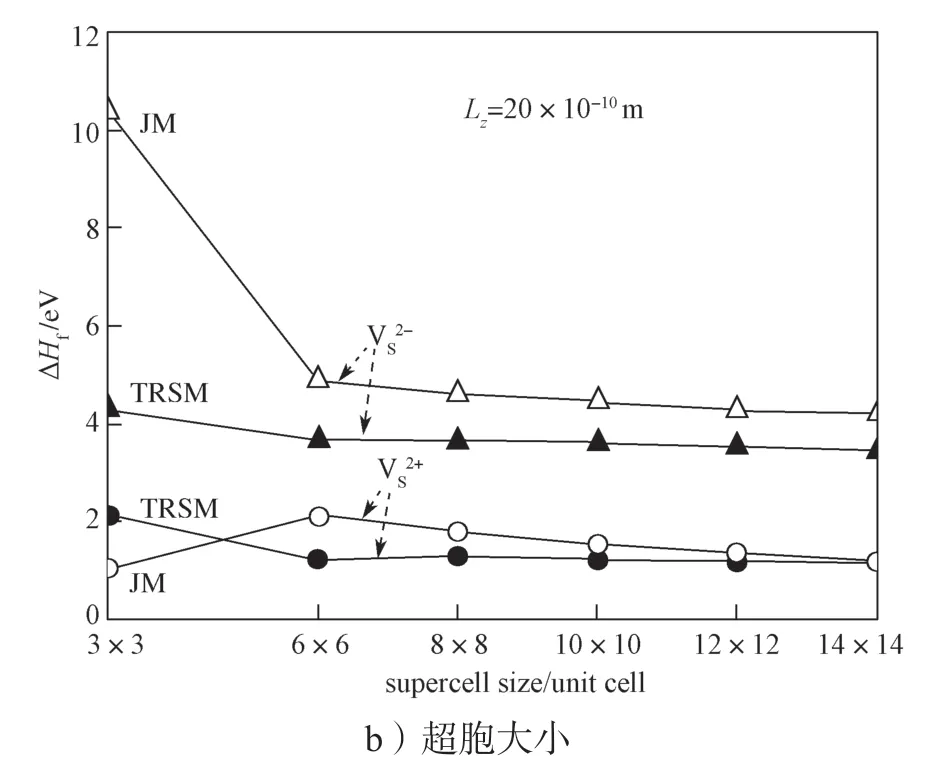
图3 单层MoS2 中S 空位的带电缺陷形成能（和）与真空层厚度和超胞大小间的关系曲线Fig.3 Relationship between the formation energy of charged defects of S vacancies ( and ) in the monolayer MoS2 and the thickness of vacuum layer and supercell size

3.2 单层MoS2 中本征点缺陷的形成能

MoS2中本征的点缺陷有单S 空位缺陷（VS）、双S 空位缺陷（VS2）、Mo 空位缺陷（VMo）、S 原子替代Mo 原子缺陷（SMo）、Mo 原子替代S 原子缺陷（MoS）、Mo 原子吸附（AMo）和S 原子吸附（AS）。其结构示意图如图4所示，图中稍小的圆球代表S原子，稍大的圆球代表Mo 原子，而缺陷位点用虚线圆圈标示出来。这些缺陷在实验制备的MoS2材料中都观测到过[52-55]。

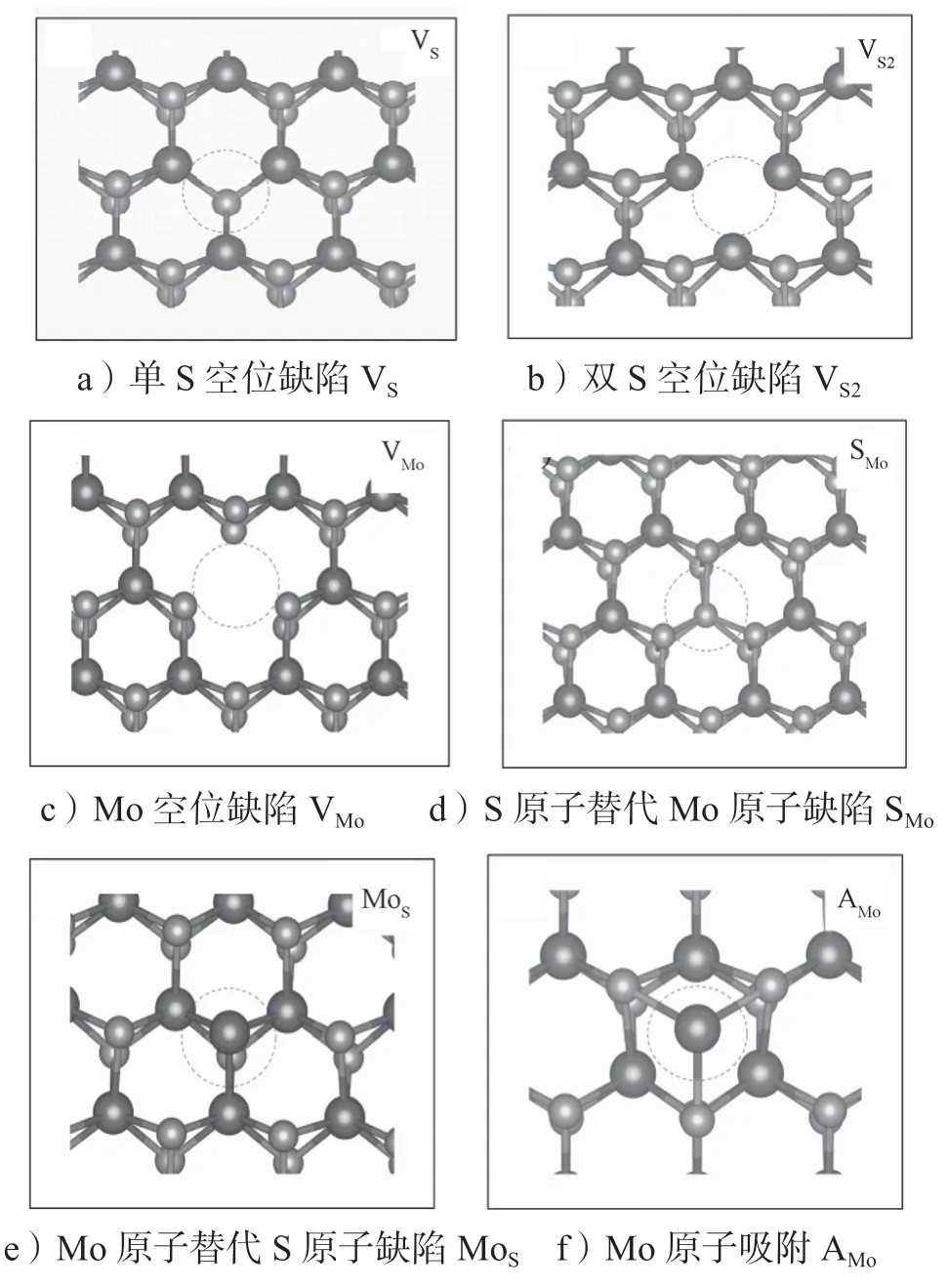
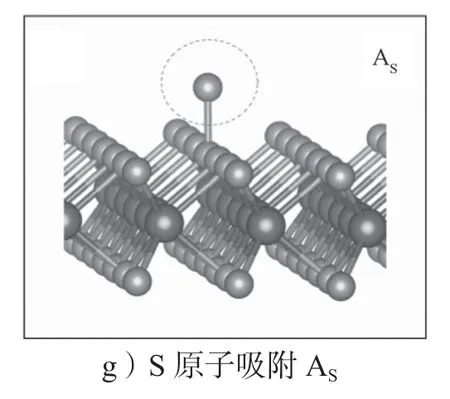
图4 单层MoS2 中的本征点缺陷结构示意图Fig.4 Schematic diagram of the intrinsic point defect structure in monolayer MoS2

本文研究了单层MoS2中上述7 种本征点缺陷的形成能，所得结果如图5所示。其中，图5a给出了中性本征点缺陷形成能与所在环境（即S 原子化学势μS）之间的关系，μS=0 eV 时，表示S 原子有富余的环境；μS=-1.30 eV 时，表示S 原子缺乏的环境。图5b给出了本征点缺陷形成能与费米能级εF之间的关系曲线，环境为S 原子有富余的环境（μS=0 eV），单层MoS2的能隙大小为1.68 eV。2+表示该缺陷带2 个电子电量的正电荷（即电离出两个电子），2-表示该缺陷带2 个电子电量的负电荷（即吸附两个电子），0 表示该缺陷电中性。

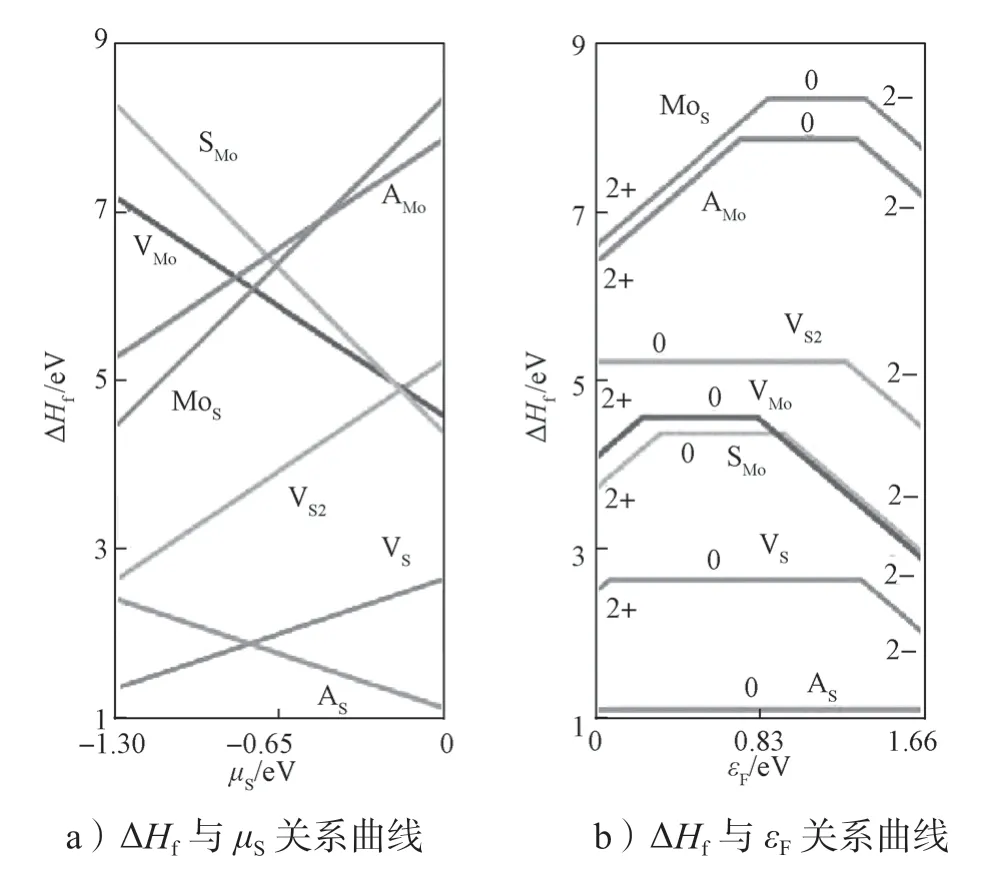
图5 单层MoS2 中7 种本征点缺陷的形成能ΔHf与μS 和εF 的关系曲线Fig.5 Formation energy ΔHf of seven types of intrinsic point defects in monolayer MoS2 as function with μS and εF

从图5a中可以看出，在S 元素缺乏的环境（μS=-1.30 eV）中，S 空位缺陷（VS）有最低的形成能，其缺陷的形成能为1.32 eV，其它缺陷的形成能都大于2.5 eV。当环境是S 元素富余的时候（μS=0 eV），S 原子吸附（AS）的形成能最低（ΔHf=1.09 eV）。这说明在MoS2中最常见的本征缺陷是VS和AS。这与实验上观测的结果吻合。相关文献的实验结果表明，通过机械剥离制备的MoS2中出现的缺陷形式最多的是VS[52-53]。

利用TRSM 模型进一步研究了这7 种本征缺陷电离后的形成能，如图5b所示。根据公式（1）和公式（3）可以得知，缺陷电离的形成能是与材料费米能级相关的函数。在单层MoS2中，费米能级处于带隙中间（即≤εF≤+1.68 eV）。在图5b中，2+线段与0 线段的交点对应的εF为施主转换能级εα(2+/0)；0 线段与2-线段的交点对应的εF为受主转换能级εα(0/2-)。由图可以看出，所有缺陷的施主转换能级εα(2+/0)都远离导带底，而受主转换能级εα(0/2-)也都远离价带顶。这意味着给出的7 种本征点缺陷的转换能级非常深，不利于缺陷电离而产生载流子。换能级εα(2+/0)到导带底的能量距离称为施主缺陷的电离能，换能级εα(0/2-)到价带顶的能量距离称为受主缺陷的电离能。电离能表示缺陷能够产生自由载流子所需要的能量。在这7 种缺陷中，MoS有最低的施主缺陷电离能，为0.80 eV；VMo有最低的受主缺陷电离能，为0.82 eV。在MoS2中，本征的点缺陷不能够为其提供有效的载流子。参照相关文献结论可知，所得的计算结果与前人的理论计算结论是一致的[52，54-56]。

3.3 MoS2 中H 原子吸附的形成能

下面研究H 原子在MoS2材料中H 原子吸附的形成能。H 原子在块体、双层和单层MoS2中的吸附位点如图6所示。图6中，大号圆球为Mo 原子，中号圆球为S 原子，小号圆球为H 原子。

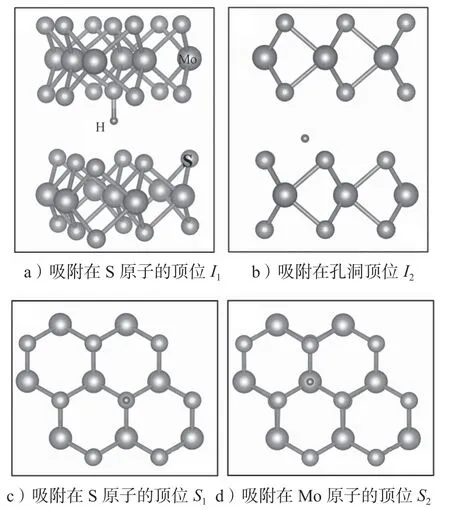
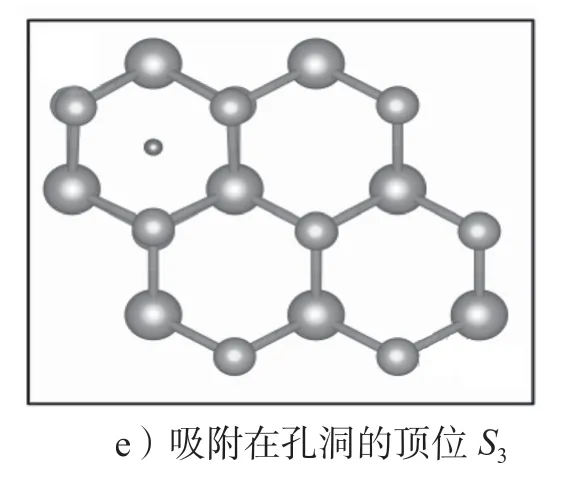
图6 H 原子在MoS2 材料中的吸附位点示意图Fig.6 Schematic diagram of the adsorption sites of H atoms in MoS2 materials

对于块体MoS2材料，其H 原子吸附在两个夹层中间，有两个高对称吸附位点：吸附在S 原子的顶位，记为I1位点，如图6a所示；吸附在孔洞的顶位，记为I2位点，如图6b所示。对于单层MoS2材料，H原子只能吸附在其表面，有如下3 个高对称位点：S原子的顶位，记为S1位点，如图6c所示；Mo 原子的顶位，记为S2位点，如图6d所示；孔洞的顶位，记为S3位点，如图6e所示。对于双层MoS2，H 原子既可以吸附在表面，也可以吸附在两层之间，因此吸附位点有5 个。表2给出了H 原子在MoS2中的吸附形成能。对于块体、双层和单层MoS2采用的超胞分别为3×3×2 倍原胞、6×6 倍原胞和6×6 倍原胞。形成能的计算中加入了范德华力修正，*标识为未进行范德华力修正。

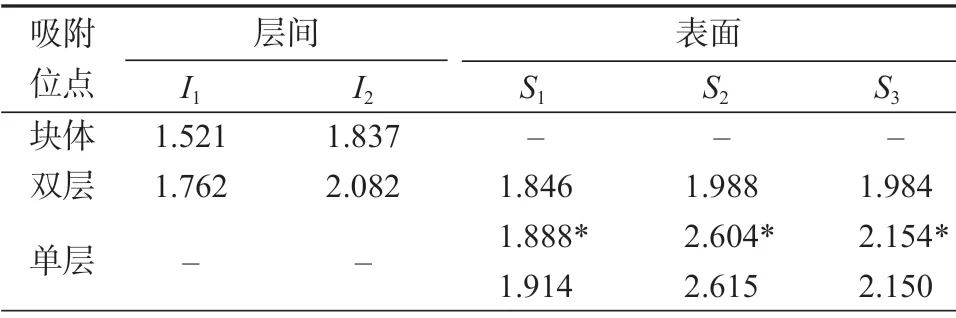
表2 H 原子吸附在MoS2 中的形成能Table 2 Formation energy of H atom adsorption in MoS2

从表2中可以得知，对于块体和双层MoS2，I1位点有最低的形成能。对于单层MoS2，S1位点的形成能要比其他位点至少低0.24 eV。H 原子趋向于吸附在S 原子上。

本文进一步研究了H原子吸附后的MoS2电离能。研究发现，在单层MoS2中，H 原子吸附的施主转换能级εα(+/0)位于CBM（conduction band minimum）上的0.01 eV。这意味着单层MoS2中的H 原子吸附可以自发地提供一个自由电子，使得材料中呈现出n型半导体。对于双层MoS2，H 原子吸附的施主电离能也只有0.19 eV。这说明MoS2材料中H 原子吸附有非常浅的转换能级，能够非常有效地提供n 型载流子。实验中测得MoS2为n 型半导体[36,57]，H 原子的吸附有可能就是MoS2表现为n 型载流子输运性质的原因。为了理解H 原子吸附能够在MoS2中产生n 型载流子的原因，给出了H 原子吸附后体系的能带示意图和电荷分布图，如图7所示，电荷分布图中的等值面值为 5.399×108C/m3。模型图中，颜色较深部分为电荷的分布区域。

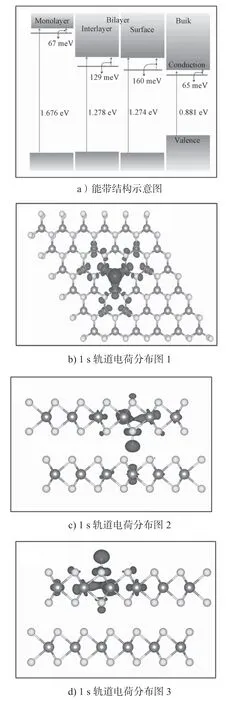
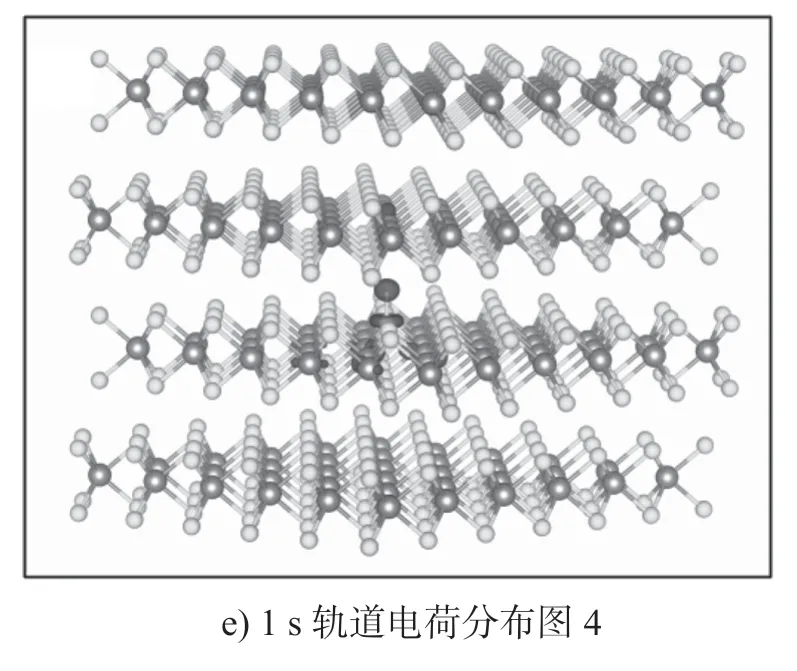
图7 MoS2 中H 原子吸附的能带和电荷密度示意图Fig.7 Energy band and charge density diagram of MoS2 with H atom adsorbed

从图7a中可以明显看到，H 原子吸附后其缺陷能级距离导带底非常近。在单层和块体MoS2中，其缺陷能级距离导带底能量差分别只有67 meV 和65 meV。在双层MoS2的夹层和表面上，这个能量差分别为129 meV 和160 meV。这使得缺陷能级上的电子能够很容易跃迁到导带底，形成自由电子。从缺陷态的电荷密度分布图（如图7所示）中也可以直观地看出，原本局域在H 原子上的1 s 轨道电子电荷密度分布明显扩散到了MoS2材料中。这一现象表明H 原子上的电荷已经被注入到MoS2材料里，形成了n 型的载流子。

4 结语

本文介绍了一个严谨的、透明的、与维度无关的半导体材料中带电缺陷计算模型——TRSM。并运用TRSM 模型系统地研究了单层MoS2中的点缺陷的形成能和电离能。研究发现，MoS2中常见的本征点缺陷因其n 型和p 型转换能级都很深，不能够为其产生有效的载流子，但是H 原子的吸附有非常浅的n 型转换能级，能够为MoS2材料提供自由电子。因此，H 原子的吸附有可能是实验上测得MoS2材料为n 型半导体的原因。