LIRA 线性共振分析技术在电缆故障诊断中的应用

李 扬 孟令强 孔 切

（国核电站运行服务技术有限公司，上海200233）

1 概述

近年来，随着我国电力行业的不断发展，电缆的利用率越来越高，其稳定性、耐久性、安全性是供电系统安全运行的前提条件，在保障设计功能和用户安全方面有着重要的作用。当电缆由于安装工艺、制造缺陷、材料的自然老化、运行环境的变化以及设备异常引起电缆故障时，将导致电力系统的不可靠运行。但是由于此类事件无法完全避免，遂当电缆发生故障时，对电缆进行准确判断和精确定位就显得尤其重要。

在当今科学技术快速发展的背景下，与电缆状态监测相关的技术也在日新月异中，如震荡波技术、红外热成像技术、局放等技术都有在工程现场中应用，虽然在电缆整体运行状态评估以及永久性故障定位方面有一定的指导意义，但无法综合的诊断电缆局部潜伏性缺陷以及反应电缆的整体老化情况，本文针对国内外现有的研究不足之处，利用Lira 线性共振分析技术来进行实际应用，测试该技术的可靠稳定性，以及在电缆故障诊断中定性、定量的能力。

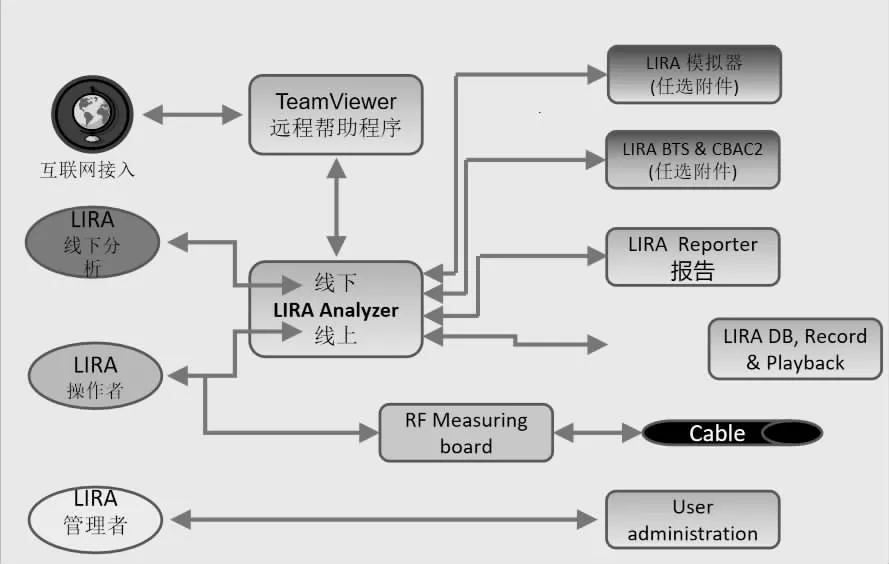
图1 Lira 原理图

图2 电缆缺陷位置示意图

2 Lira 技术原理

线性共振分析（Lira）监测技术基于宽带频率域分析，对无匹配传输线的高频谐振效应进行分析，且对绝缘介电常数这些电气参数的微小变化较为敏感，虽然不同种类的电缆有不同的结构（绝缘类型、几何结构）和其他非老化因素的影响，但线性共振分析技术仍能检测并定位出性质变化的地方，原理如图1 所示。

可以检测出以下几种电缆故障问题：

a.各种影响绝缘电容的变化。

b.电缆尺寸的变化，例如受大量的热、辐照、水侵入、腐蚀、弯曲、刮擦、机械冲击、疲劳等影响的电缆接头或不同电缆的连接处。

c.绝缘材料的老化（XLPE、PILC 等）。

d.大多数情况下，电缆的显著特性或沿着电缆的整体老化（多次测量可以预测这些特征/老化的发展趋势）。

3 测试与分析

3.1 缺陷设置

为了满足现场可能会出现的问题，使用一根长电缆（总长430m），并在电缆的一端设计了如图2 所示的10 个缺陷，电缆不剪短，剩余部分留在卷线盘中，用来测试Lira 能否识别缺陷和反映缺陷的严重程度。

3.2 分析优化

Lira 测试后需要使用分析软件对其测试结果进行优化，通常需要检查谱图验证带宽是否选择正确,检查结果选项卡的VR数值,如果无明显差别，查看结果表或利用DNORM选项卡查看图形结果。如果有相位偏移，需要使用探头补偿和信号带宽来达到所需的相位谱形式。

另外在极个别情况下，由于电缆测试时的外部噪声和一些干扰因素，系统在找寻归一化参数时会遇到若干问题。需要进行手动调节，在Norm 图中转为手动优化，调节Term Tolerance（截断）和Horizon（范围）按钮，使得每个周期的谐波波形无限相似，每个周期的谐波波形越相似，测试结果越能反应电缆的真实情况。如图3 所示。

3.3 测试结果

经过数据优化，得到的测试结果如图4 所示。

3.4 结果分析

3.4.1 周向缺陷

结合DNORM-Location 图，发现周向1/4，周向1/2,周向1/1的三个缺陷都能被Lira 识别，但是无法分辨缺陷的损伤程度。

3.4.2 流向缺陷

结合缺陷图，Lira 可以发现流向方向10mm，20mm，50mm 的缺陷，但是无法通过缺陷图来判断电缆的损伤情况。

3.4.3 挤压折叠

结合图谱，Lira 可以发现被挤压和折叠状态下的电缆异常情况，通常电缆在折叠情况下的损伤程度要大于挤压，但是Lira未能定量的反应该情况。

3.4.4 浸油

试验室中用保鲜膜浸油包裹电缆约14 天左右，试验前后该处未能在Lira 中正常的被显示，可能由于时间过短，未对电缆造成实质性的损伤，遂未能在图谱中显示该缺陷。

3.4.5 外护套打薄

Lira 对外护套的微小变化极为敏感，在此次的试验中发现了该缺陷。

4 结论

4.1 Lira 在测试完成后，曲线经过分析处理可以准确的得到电缆的相关状态情况。

4.2 通过将测试缺陷图和实际缺陷图进行对比，最大的误差为0.6m，可以看到Lira 的测试结果可靠稳定。

图3 Norm 曲线优化图

图4 测试结果图

4.3 通过比对每种类型缺陷的测试结果，每种类型损伤程度的不同，不能在Lira 的结果中正确反应，遂Lira 无法定量的反应电缆的损伤程度。