基于模糊故障树和贝叶斯网络的矿井提升机故障诊断
张梅,许桃,孙辉煌,孟祥宇
(1.安徽理工大学 电气与信息工程学院, 安徽 淮南 232001;2.淮北矿业(集团)有限责任公司 许疃煤矿, 安徽 蒙城 233500)
0 引言
矿井提升机是煤矿运输过程中关键机械设备,一旦发生故障,将对煤矿生产造成极大损失。在提升机发生故障时快速准确地找到故障原因和故障点,对于保证其安全可靠运行具有重要意义[1-3]。许多学者在矿井提升机故障诊断方面进行了大量研究。董黎芳等[4]将支持向量机应用于矿井提升机制动系统的故障诊断,但只适用于少量样本的诊断,准确性不高;李加昭[5]提出了基于BP神经网络与D-S证据理论二次融合的多源数据融合方法,实现了多样本参数的矿井提升机故障诊断及预测,但建模过程过于复杂,无法快速诊断;魏志成[6]利用故障树分析法对提升机进行故障诊断,将系统的故障状态作为顶事件,将可能引起顶事件发生的所有直接与间接原因作为底事件,使用树形图的方式表示一个系统中顶事件与底事件之间的逻辑关系,根据故障树中各底事件发生概率计算出顶事件发生概率,解决了建模复杂的问题,但实际中底事件发生概率难以确定;田晓翠[7]将模糊数学理论与故障树分析法相结合,利用模糊故障树分析法进行矿井提升机故障诊断,将底事件发生概率替换为某个区间,通过模糊运算得到底事件模糊概率,克服了常规故障树分析法中确定底事件发生概率困难的缺点,但反向推理能力较弱,诊断效率不高;李娟莉等[8]将贝叶斯网络和A-star算法运用于矿井提升制动系统故障诊断,在故障发生后进行反向推理,快速定位故障点,但网络构造较为困难。在上述研究的基础上,本文综合模糊故障树和贝叶斯网络的优点,提出了一种基于模糊故障树和贝叶斯网络的矿井提升机故障诊断方法,可快速、准确诊断提升机故障类型和故障点。
1 矿井提升机故障诊断原理
基于模糊故障树和贝叶斯网络的矿井提升机故障诊断包括基础数据处理、模糊故障树分析和贝叶斯网络分析3个部分,如图1所示。首先对采集的提升机运行参数进行预处理和多源信息融合,以去除无用的数据,并提取数据特征值,保证数据的准确性;然后将处理后的数据输入矿井提升机模糊故障树进行初步计算,得到相应底事件模糊概率;最后根据映射规则将模糊故障树映射为贝叶斯网络,将底事件模糊概率作为先验概率,计算叶节点发生概率、根节点的后验概率、概率重要度和关键重要度,从而确定故障类型和位置。
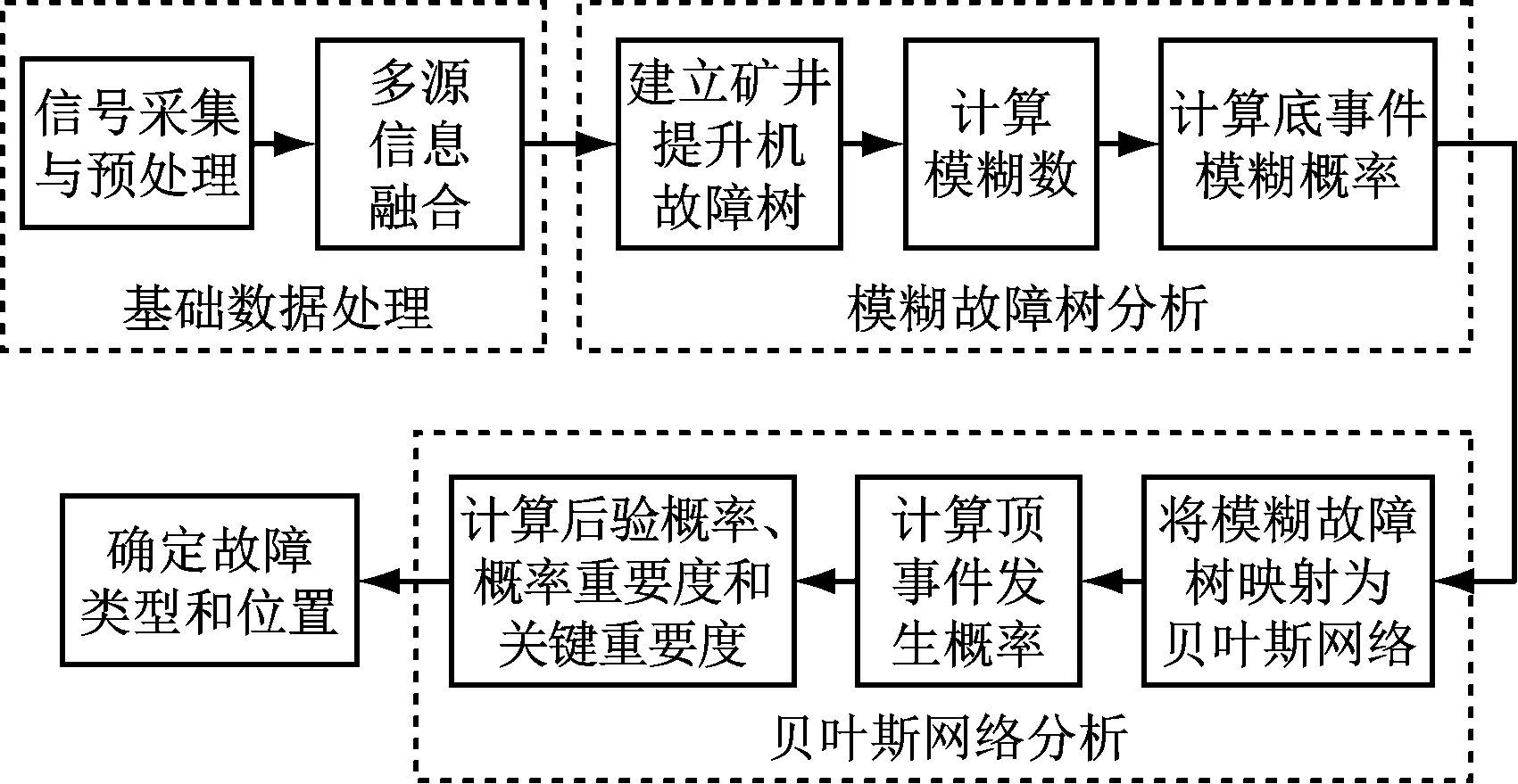
图1 基于模糊故障树和贝叶斯网络的矿井提升机故障诊断原理Fig.1 Fault diagnosis principle of mine hoist based on fuzzy fault tree and Bayesian network
1.1 矿井提升机相关基础数据处理
通过电流、电压、位移、温度、油压、拉力等多种形式的前端信号传感器对提升机运行参数进行实时采集。由于提升机工作环境复杂及其他客观因素影响,采集的数据含有干扰和噪声,需要对采集的数据进行去噪预处理(如零均值化、趋势项消除、归一化和滤波等)。将预处理后的数据进行多源信息融合(多源信息融合方法包括深度学习法、D-S证据理论法、主元分析法、卡尔曼滤波法等[9-11]),获得能准确反映提升机实时运行情况的特征向量,使后续的可靠性分析更加准确。
1.2 矿井提升机模糊故障树分析
矿井提升机结构体系庞大、工作环境复杂,出现故障的原因种类繁多,本文对提升机常见故障进行分析归纳[12-13],建立了矿井提升机故障树,如图2所示。其中编码及对应故障事件见表1。

表1 矿井提升机故障事件Table 1 Fault events of mine hoist
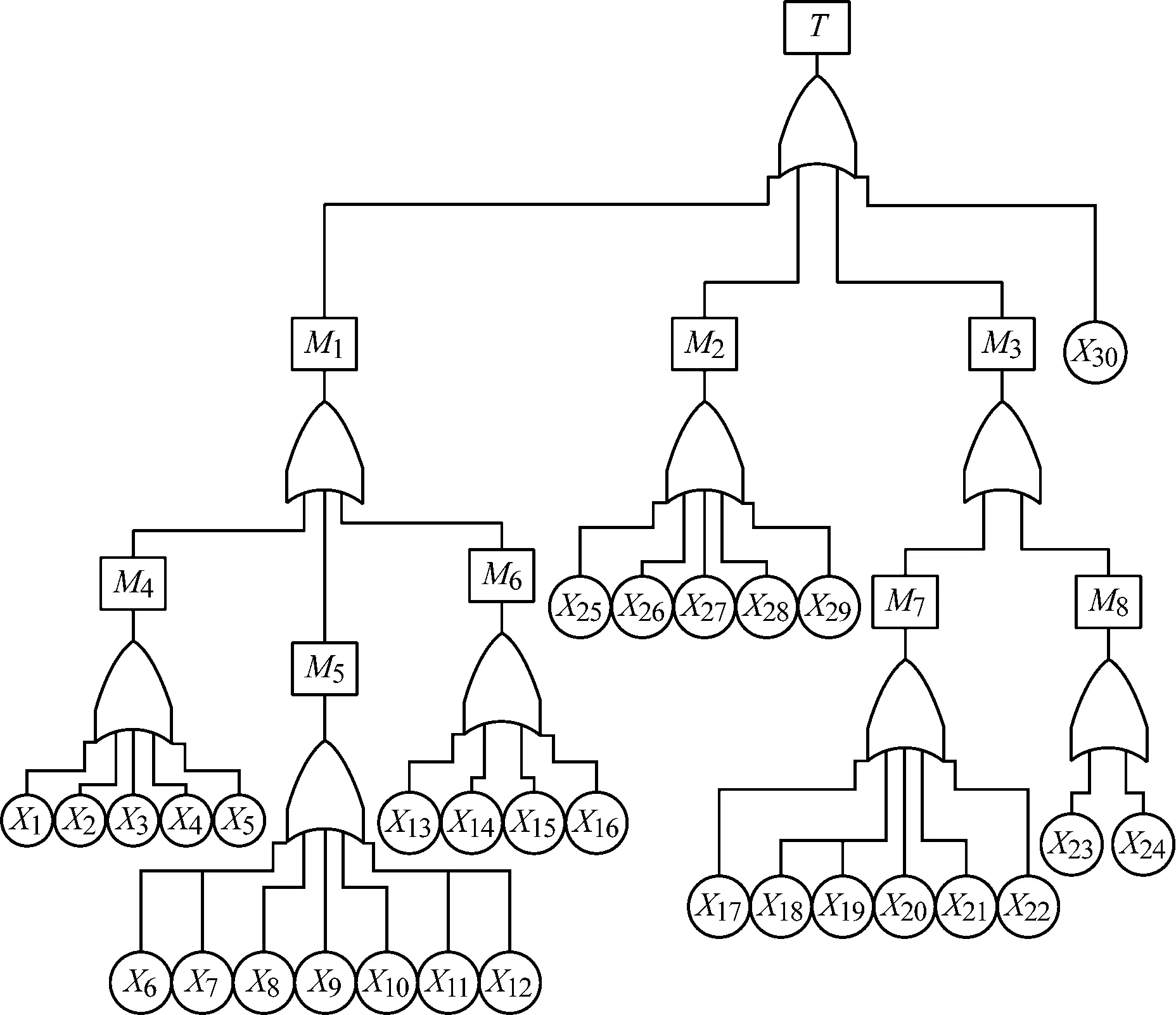
图2 矿井提升机故障树Fig.2 Fault tree of mine hoist
在矿井提升机故障树中,受环境及其他因素的影响,底事件发生概率具有模糊性,实际很难给出一个精确的概率,因此采用模糊数表示提升机底事件发生概率。模糊数的表示方法有三角模糊数、梯形模糊数和正态模糊数等[14],本文采用三角模糊数。
三角模糊数的隶属度函数为
(1)
则底事件Xi(i=1,2,…,n,n为底事件数)发生概率为
PXi=(mi-αi,mi,mi+βi)
(2)
式中:αi,βi为PXi的置信上下限;mi为底事件发生概率中值,0<αi≤mi≤βi。
矿井提升机故障树中仅使用了逻辑或门,引入或门模糊算子,可得底事件模糊概率:

(3)
1.3 基于贝叶斯网络的矿井提升机可靠性分析
将模糊故障树映射为贝叶斯网络的具体过程[15-17]:① 将模糊故障树中的事件对应表达为贝叶斯网络中的节点,其中,模糊故障树中的底事件在贝叶斯网络中作为根节点,顶事件在贝叶斯网络中作为叶节点。② 将模糊故障树中各底事件模糊概率作为贝叶斯网络中对应根节点的先验概率进行赋值。③ 将模糊故障树中的逻辑门对应表达为贝叶斯网络的节点条件概率分布。
根据矿井提升机模糊故障树转换的贝叶斯网络如图3所示。
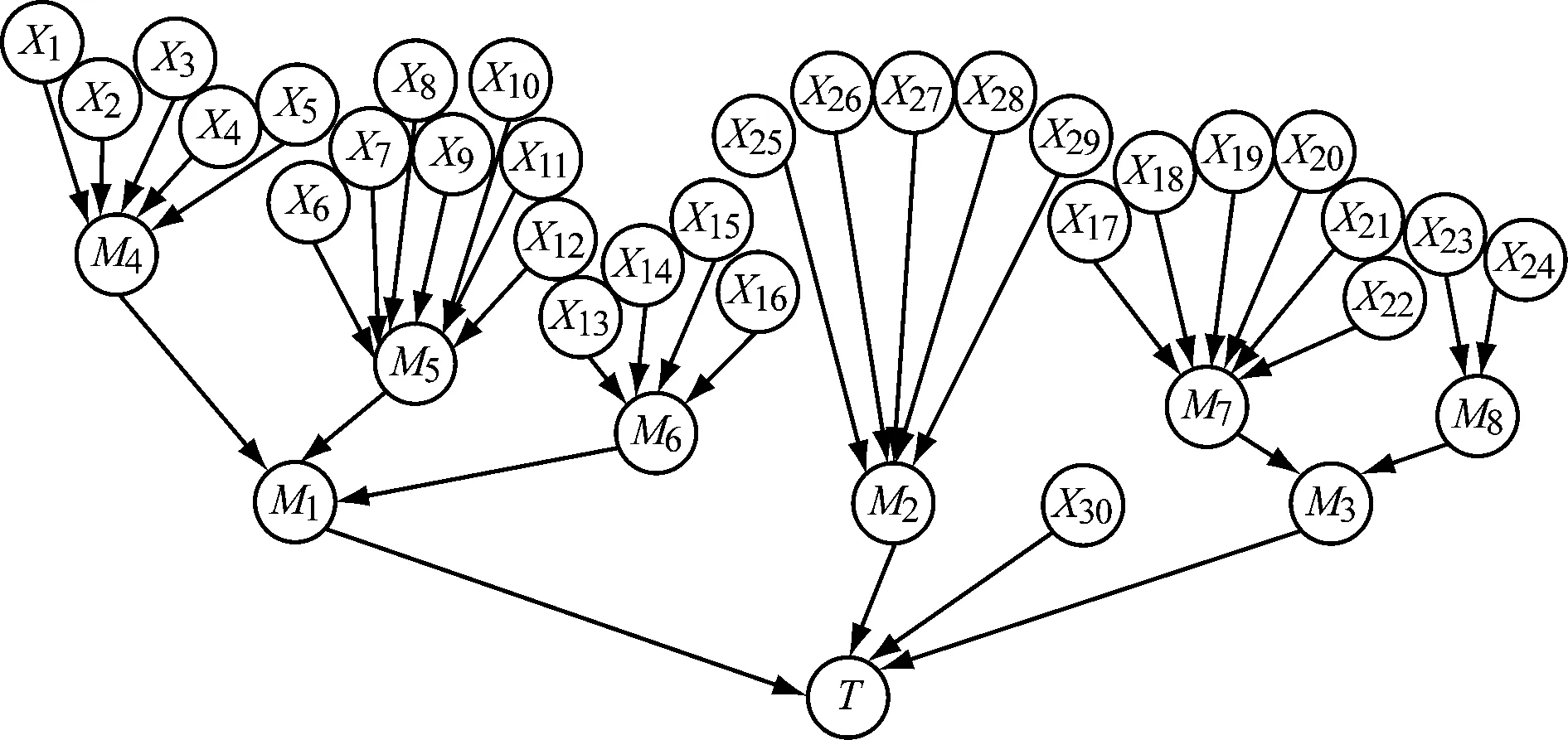
图3 矿井提升机故障贝叶斯网络Fig.3 Bayesian network of mine hoist failure
贝叶斯网络分析是根据先验概率求得叶节点发生概率,进而求得根节点的后验概率,但根据各根节点后验概率指导故障诊断具有不完全可靠性。通过根节点概率重要度可反映根节点引起叶节点故障发生的重要程度,根节点关键重要度可反映降低提升机可靠性的薄弱环节。因此需要综合比较各根节点的后验概率、概率重要度和关键重要度,得出引起提升机故障的主要事件。
矿井提升机故障贝叶斯网络中叶节点为T,根节点为X1—X30,且X1∪X2∪…∪X30=∅,则叶节点T发生的情况下,各根节点Xi发生概率(也称为后验概率)为
(4)
式中:P(Xi)为根节点Xi的先验概率;P(T|Xi)为根节点Xi发生的情况下叶节点T发生概率。
根节点Xi状态为Q1(根节点故障时Q1为1,根节点无故障时Q1为0)的概率为
(5)
式中Pa(Xi)为根节点Xi的条件概率。
叶节点T状态为Q2(叶节点发生时Q2为1,叶节点不发生时Q2为0)的概率为
P(T=Q2)=P(T=Q2|X1,X2,…,Xn)×
P(X1)P(X2)…P(Xn)
(6)
根节点Xi状态为Q1时,叶节点T状态为Q2的概率为
(7)
根节点Xi状态为Q1时单独引起叶节点T状态为Q2的概率重要度为
P(T=Q2|Xi=0)
(8)
根节点Xi对于叶节点T状态为Q2的概率重要度为
(9)
式中K为根节点故障数。
根节点Xi状态为Q1时单独引起叶节点T状态为Q2的关键重要度为
(10)
根节点Xi对于叶节点T状态为Q2的关键重要度为
(11)
2 应用及结果分析
以淮北矿业(集团)有限责任公司许疃煤矿主提升机液压制动部分故障为例,查阅提升机现场运行情况及检修记录,走访相关专家、技术人员,综合各类参考资料,可得提升机各底事件发生概率中值mi和置信上下限αi,βi估计值(按提升机连续工作300 h计算),见表2。
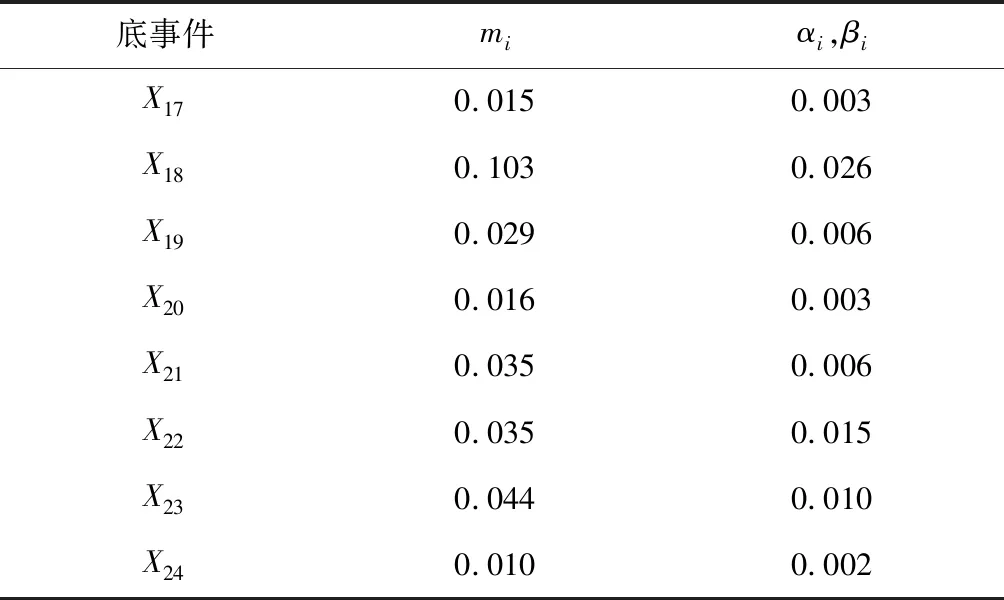
表2 底事件发生概率中值与置信上下限Table 2 Median and upper and lower confidence limits of bottom events probability
将表2中数据代入式(3),得到提升机各底事件模糊概率,见表3。

表3 底事件模糊概率Table 3 Fuzzy probability of bottom events
将表3中各底事件模糊概率作为先验概率,当顶事件发生时,利用贝叶斯网络的反向推理能力对先验概率进行修正,根据式(4)求得各根节点后验概率,见表4。将提升机故障树中液压制动部分的或门逻辑关系转换为贝叶斯网络中各根节点的条件概率,根据式(6)可得液压制动部分故障发生概率约为0.339。
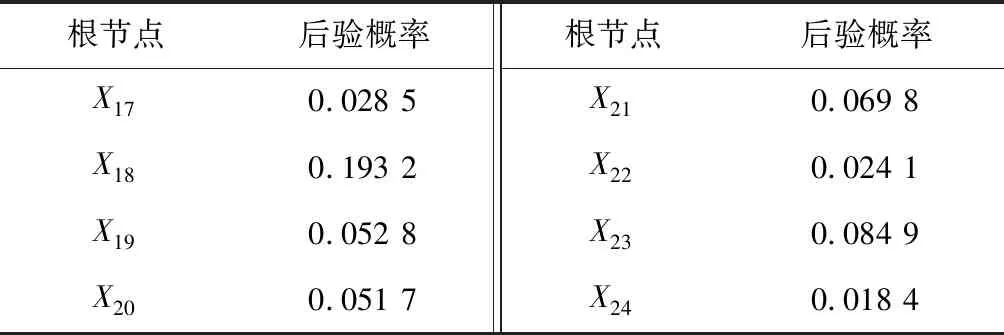
表4 根节点后验概率Table 4 Posterior probability of root nodes
根据式(8)—式(11)求得各根节点在提升机液压制动部分故障时的概率重要度和关键重要度,见表5。
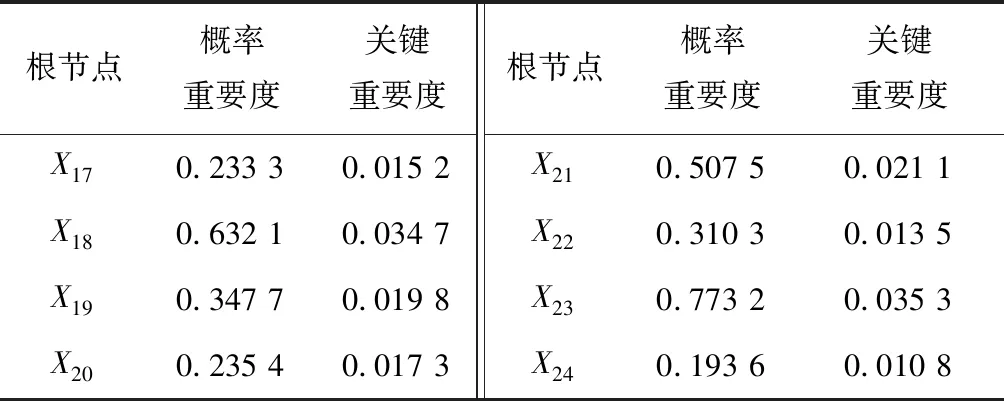
表5 根节点概率重要度和关键重要度Table 5 Probability importance and key importance of root nodes
综合考虑根节点的后验概率、概率重要度和关键重要度,可看出X18,X23,X213个事件对提升机液压制动部分故障的影响较大。当故障发生时,优先排查这3个事件,再对其他事件进行逐次排查,极大缩短了提升机故障诊断时间,提高了故障诊断的实时性。
3 结语
提出了一种基于模糊故障树和贝叶斯网络的矿井提升机故障诊断方法。首先对采集的提升机运行参数进行去噪预处理,并进行多源信息融合以获得完整信息;然后将处理后的数据输入矿井提升机故障树,计算底事件的模糊数和模糊概率;最后将模糊故障树映射为贝叶斯网络,将底事件模糊概率作为先验概率,计算叶节点发生概率,进而获得根节点的后验概率、概率重要度和关键重要度,并依此进行快速故障诊断。以矿井提升机液压制动部分故障为例进行分析,验证了该方法的可行性。

