基于阈值分割法和卷积神经网络的图像识别算法

李鹏松, 李俊达, 吴良武, 胡建平

(1. 东北电力大学 理学院, 吉林 吉林 132012； 2. 大连测控技术研究所, 辽宁 大连 116013)

0 引 言

在计算机视觉领域, 图像识别问题一直备受关注[1]. 卷积神经网络(convolutional neural network)是完成图像识别任务的主要方法之一. 为达到对图像更好的识别效果, 研究者们开始不断改进卷积神经网络的结构, 在改进过程中卷积神经网络的深度和参数量不断增加[2-4], 使卷积网络产生两点不足[5-7]： 1) 网络的识别性能过分依赖于数据量； 2) 网络在训练过程中, 收敛速度慢, 计算成本高. 数据增强和减少参数量是解决卷积神经网络存在不足的有效方法, 将两者结合用于改进卷积网络, 可使网络在数据量较少的任务中取得理想的识别性能[8].

均值迭代阈值分割法是一种经典的阈值分割方法, 因其运算量小而被广泛应用[9]. 由于卷积神经网络无法直接提取图像目标的特征, 只能逐渐聚焦于图像目标[10], 因此, 卷积神经网络需大量的训练数据和参数, 用以区分图像的目标和背景. 均值迭代阈值分割法可增强图像目标, 使卷积神经网络在池化操作中舍弃无用的背景特征, 降低图像背景对识别效果的干扰, 即通过阈值分割法简化识别任务, 进而减少卷积神经网络所需的训练数据量和参数量. AlexNet是深度最小的卷积神经网络之一, 因其参数较少被广泛应用于实际应用中[11]. 但在数据量较小时, AlexNet识别准确度较低且收敛速度较慢, 其原因是： 1) 卷积核步长过大, 使大量图像特征丢失, 增加了所需的训练数据量； 2) 池化步长较短, 使许多特征被重复选择, 浪费了有效计算资源.

根据上述分析, 本文提出一种基于均值迭代阈值分割法和卷积神经网络的图像识别算法. 首先用均值迭代阈值分割法区分图像的目标和背景, 并扩大两者灰度值之间的差异; 然后改进卷积神经网络适应处理后的数据, 并识别测试集数据; 最后, 计算出测试集的识别准确度和损失值, 作为评价算法识别性能的指标. 本文算法流程如图1所示.

图1 本文算法流程Fig.1 Flowchart of proposed algorithm

1 均值迭代阈值分割法

均值迭代阈值分割法的基本思想是利用图像的目标和背景在灰度特性上的差异, 把图像视为具有不同灰度级两类区域的组合, 通过阈值T把像素划分为两类----目标和背景.

均值迭代阈值分割法步骤如下：

1) 初始化阈值, 本文使用图像的灰度平均值；

2) 用阈值T将图像的像素分为G1和G2两部分,G1所包含的灰度值大于T, 否则属于G2；

3) 分别计算G1和G2中所有像素的灰度均值μ1和μ2；

4) 更新阈值T=(μ1+μ2)/2；

5) 重复步骤2)～4), 直至相邻两次的均值变化小于限定值；

6) 用最后确定的阈值T′进行分割,G1为目标,G2为背景.

图2为利用均值迭代阈值分割法进行区域分割的实例.

图2 均值迭代阈值分割法分割实例Fig.2 Example of mean iteration threshold segmentation method

2 AlexNet结构及改进

Krizhevsky等[11]建立了AlexNet, 其特点是参数量较少, 运算成本较低, 其网络结构如图3所示. AlexNet的首层卷积核步长较大、 池化操作步长较小, 使网络在卷积核提取特征时丢失了部分特征, 在池化操作选择特征时重复选择部分特征. 同时, AlexNet全连接层参数量为58 621 955, 约占总参数量的96%, 大部分运算成本集中在全连接层. 因此, 本文主要针对卷积神经网络严重依赖数据量的问题进行改进, 目标是使卷积神经网络在训练数据较少时也可达理想的识别效果. 因此, 本文以层数和参数较少的AlexNet为基础改进卷积神经网络, 改进后的卷积网络结构如图4所示, 其中N为图像边长,n为图像种类数.

图3 AlexNet结构示意图Fig.3 Structure diagram of AlexNet

图4 改进的卷积网络结构示意图Fig.4 Structure diagram of improved convolutional neural network

本文算法改进主要有以下几点：

1) 在卷积层上, 为提取图像更多的局部特征, 增加了前两层的卷积核个数, 并缩小了前两层卷积核的尺寸和步长；

2) 在池化层上, 为防止在选择特征时出现重复, 将池化步长增加为2；

3) 在全连接层上, 图像经过均值迭代阈值分割后, 无效图像像素数量大幅度减少, 因此, 本文将全连接层所需的参数量降低了50%以上.

3 改进算法设计

本文以减少算法参数量和所需的训练数据量为目的, 结合均值迭代阈值分割法与改进后的卷积神经网络对图像进行识别. 图像识别算法步骤如下：

1) 用均值阈值迭代法求出图像目标和背景的分界值, 区分背景和目标；

2) 处理背景像素的灰度值；

3) 用处理后的图像训练卷积神经网络模型, 并计算每次迭代结果的识别准确度和损失误差；

4) 根据卷积神经网络的收敛情况确定模型参数, 输出测试集的识别准确度和损失误差.

均值迭代阈值分割法主要用于区分图像的背景和目标, 处理背景像素的灰度值以扩大图像目标与背景灰度值之间的差异； 卷积神经网络主要用于图像的识别, 网络通过卷积核提取图像特征, 通过池化层选择特征. 均值迭代阈值分割法可减少卷积神经网络的参数及所需的数据量, 其原理如下：

1) 被弱化后的背景特征因其激活值较小极易被池化操作滤除, 因此, 卷积神经网络的权重更新主要受图像目标影响, 网络只需少量样本即可提取图像目标的特征, 从而减少网络所需的训练数据量和参数量;

2) 均值迭代阈值分割法减少了无效像素的数量, 因此可减少全连接层所需的参数量, 由于卷积神经网络的参数主要集中在全连接层, 因此本文即使增加了少量卷积核的个数, 但总的参数量仍降低50%以上.

本文算法中的卷积神经网络主要由卷积层、 池化层和分类器组成[12]. 卷积层计算公式为

(1)

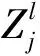
(2)

池化层主要对每层得到的特征进行选择, 本文采用最大池化对特征进行选择. 池化后的特征将作为分类器的输入, 对图像进行识别. 本文使用的分类器为Softmax, 计算公式为

(3)

其中:zj为输出层第j个神经元的输出值;pij为第i个样本属于第j类的概率值. 本文算法使用梯度下降法训练卷积神经网络, 通过不断迭代更新权重, 其权重更新规则为

(4)

4 实 验

4.1 实验设置

实验在Tensorflow 1.5.0上实现, 最大迭代次数为500, 学习率为0.000 1, 参数的初始值设为服从均值为0的高斯分布. 本文用数据的平均识别准确率评价算法的识别准确度, 用数据的平均损失值评价算法的识别误差, 用收敛速度评价算法的运算成本[14]. 平均识别准确率和平均损失值的计算公式分别为

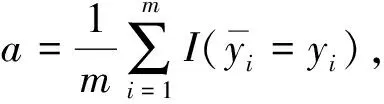
(5)

(6)

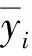
本文使用3组数据集对算法进行验证, 其中训练集占80%, 测试集占20%, 数据集的基本信息列于表1. 分别用AlexNet,VGGNet和本文算法对3组数据集进行实验, 检验本文算法的识别性能. 选择AlexNet和VGGNet作为对比算法的原因： AlexNet和VGGNet分别为深度学习中深度最小和宽度最小的卷积神经网络之一, 参数量小于其他卷积神经网络[15-19], 因此, 相比传统卷积神经网络更适合样本数较少的识别任务.

表1 实验所用数据集基本信息

4.2 结果分析

用基于均值迭代阈值分割法和卷积神经网络的图像识别算法分别识别Dog&Cat,Cifar-10和 Corel-1000数据集, 实验结果列于表2. 由表2可见, 本文算法的测试集平均准确率分别约为98.8%,96.2%,97.5%, 具有较高的平均识别准确率, 验证了算法的优越性. 在Dog&Cat数据集上, 算法的平均准确率最高, 平均损失最小, 其原因是算法类别数较少, 识别任务简单. 本文算法识别效果符合客观规律, 验证了算法的合理性： 在Cifar-10数据集上, 算法的平均准确率最低, 平均损失最大, 其原因是图像尺寸相比于卷积核尺寸较小, 但识别结果并未因为结构问题出现巨大差异, 体现了算法在数据量不足识别任务中的普适性; 在Corel-1000数据集上, 算法的平均准确率与平均损失均居中等. 本文算法在3个数据集上的平均准确率与平均损失虽然不同, 但均大于人眼的识别准确率(94.9%), 进一步验证了该算法的优越性.

表2 训练结果随迭代次数的变化

为进一步评价算法的识别性能, 分别使用AlexNet和VGGNet对3组数据集进行识别. 将在测试集中出现的最高平均准确率作为算法最终的识别准确率, 将达到最终平均识别准确率时的最小平均损失值作为算法最终的平均损失值, 识别结果列于表3. 由表3可见: 在平均准确率与损失误差方面, 本文算法优于AlexNet和VGGNet; 在Dog&Cat数据集上, 本文算法的平均准确率比AlexNet和VGGNet分别高3.8%和1.3%, 平均损失值分别低0.176和0.053； 在Cifar-10数据集上, 本文算法的平均准确率比AlexNet高3.7%, 平均损失值低0.088； 本文算法的平均准确率比VGGNet高2.5%, 但本文算法的平均损失值低于VGGNet； 在Corel-1000数据集上, 本文算法的平均准确率比AlexNet和VGGNet分别高3.7%和6.2%, 平均损失值分别低0.116和0.122. 平均准确率的提升和平均损失值的降低, 进一步说明本文算法在样本数较少的情况下识别性能优于传统卷积神经网络, 对数据量的依赖程度更低.

表3 不同算法实验结果对比

卷积神经网络的收敛速度直接决定网络的训练时间, 快速收敛的网络只需较少的迭代次数即可确定网络的参数, 进而节省运算成本. 因此, 本文比较了3种算法在不同数据集上的收敛速度, 结果如图5所示, 其中各算法的收敛点(首次到达最终平均识别准确率的点)用三角形标记.

图5 测试集平均准确率对比Fig.5 Comparison of average accuracy on test set

由图5(A)～(C)可见： 在Dog&Cat数据集上, 本文算法在迭代150次时收敛, 识别准确度基本不变, 而AlexNet和VGGNet分别在200次和230次迭代时逐渐收敛, 同时, AlexNet和VGGNet在训练过程中, 平均准确率一直出现明显波动, 不利于网络参数的最终确定； 在Cifar-10数据集上, 本文算法在280次迭代时收敛, AlexNet在340次迭代时收敛, VGGNet在380次迭代附近收敛, 3种算法的收敛速度均较慢, 但本文算法仍比AlexNet和VGGNet的收敛速度快； 在Corel-1000数据集上, AlexNet和VGGNet分别在310次和330次时收敛, 本文算法在第260次迭代时收敛. 因此, 本文算法的收敛速度更快、 平均准确率更稳定、 识别效果更好, 进一步验证了本文算法具有较好的识别性能, 可用于样本数量不足时的识别任务. 由图5(D)可见: 算法在Corel-1000数据集和Dog&Cat数据集上具有较好的识别效果, 这是由于这两个数据集的背景区域更复杂, 均值迭代阈值分割法可有效发挥作用； 算法在Cifar-10上的识别性能改进不显著, 这是由于卷积网络的前两层卷积核尺寸和步长相比于图像尺寸过大, 提取的信息相对较少； 虽然3组数据背景的复杂程度不同, 但本文算法的识别效果仍较理想, 可用于样本数量不足时的识别任务. 因此, 本文算法适用于背景区域复杂、 图像尺寸较大、 样本数量不足的图像识别问题.

综上所述, 针对传统卷积神经网络严重依赖数据量的问题, 本文提出了一种基于均值迭代阈值分割法和卷积神经网络的图像识别算法. 在Dog&Cat,Cifar-10和Corel-1000数据集上的测试结果表明, 该算法对数据量的依赖程度较小, 在样本数量不足的图像识别任务中仍有较好的识别性能, 比传统卷积神经网络有更高的识别准确度、 更低的损失值和更快的收敛速度.