基于模糊PID的柔性膜放卷张力控制

（武汉工程大学 电气信息学院，武汉430205）

卷到卷（roll-to-roll，R2R）制造指柔性基板通过卷绕方式进行加工和装配，具有通用性强、适合批量制造的特点，广泛应用于造纸、印刷、纺织、轧钢等传统领域，近年来也开始应用于RFID 电子标签、薄膜太阳能电池等柔性电子领域[1-2]。

由于柔性基板的可拉伸特性，基板在卷绕过程中发生形变从而产生张力，柔性电子制造工艺要求设备在低张力高速度下保持较高的控制精度。放卷系统位于卷绕设备的前端，放卷张力的控制精度至关重要，会直接影响后续工位的加工精度和产品质量。时变卷径和相关工艺要求的频繁启停使得放卷过程呈现出时变和非线性特性，对放卷张力控制提出了较高的要求[3]。工业上张力控制多采用固定参数的PID控制器，难以保证整个放卷过程的张力控制精度，启停时的张力抖动也难以得到有效抑制[4]。文献[5]中建立了卷绕设备包含时变卷径的全区段张力模型，但并未研究速度扰动对张力的影响。近年来H∞控制被用来解决张力控制中的不确定性扰动问题，但控制器参数求解过程的计算量大，控制实时性难以保证[6-7]。

模糊PID控制不需要精确的数学模型，能较好地处理时变、非线性等问题，鲁棒性强，响应速度快，在电机控制领域得到了较广泛的应用[8-9]。本文在基板动力学的研究基础上，建立放卷系统的基板张力和速度模型，放卷张力设计为串级控制模式并采用模糊PID 张力控制器，有效抑制了时变卷径和速度扰动的影响，并通过仿真实验进行了验证。

1 放卷系统数学模型

1.1 单段基板的动力学模型

卷绕设备中辊轴众多，通常按相邻驱动辊来划分张力区段，研究基板动力学，如图1所示。其中L是基板在相邻辊轴间的跨距，v1，v2分别为对辊1 和对辊2的转速，ρ1，ρ2，ε1，ε2和T1，T2分别为基板进入对辊1 前后的密度、应变和张力。

图1 相邻驱动辊之间的基板张力Fig.1 Web tension between two consecutive driven rolls

假定基板是理想弹性体，基板只有纵向形变（即横截面A 不变），基板与辊轴之间无滑动（即基板速度等于辊轴转速）。已知长度l0的基板拉伸后的长度l=l0（1+ε），其中ε为基板应变。该段基板拉伸前后质量不变，即ρAl=ρ0Al0，其中ρ，ρ0为拉伸前后的基板密度，对于微小拉伸量，1/（1+ε）≈1-ε，则得：

基于质量守恒定律，可知基板流入前辊轴的质量等于基板流出后辊轴的质量加上基板经拉伸后在跨距L0长度内的质量变化，得：

将ρ1，ρ2用式（1）表示，代入式（2），得到基板应变与速度的关系式如下：

根据胡克定律，张力和应变的关系如下：

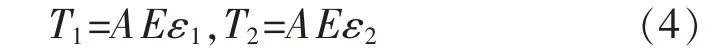
式中：A为基板横截面；E为基板杨氏模量。

联立式（3）和式（4），求得单段基板的张力方程：

1.2 放卷系统的张力和速度模型

放卷系统按张力区段进行简化，如图2所示。其中Tu为放卷区的基板张力，T0为放卷卷筒内层基板间摩擦所造成的基板张力，vu，vd分别为放卷辊和对辊的速度，L1为放卷辊和对辊之间的基板跨距，Rc为放卷辊的轴芯半径，Ru为料卷的卷径。

图2 放卷系统的简化示意图Fig.2 Simplified sketch of the unwinding system

参照单段基板的动力学模型，可写出放卷系统的基板张力Tu方程：

对于对辊，前后基板张力差对其产生正向力矩，驱动电机对其产生正向力矩，由力矩平衡方程得：

式中：Bfd为对辊的轴承粘滞摩擦系数；Id，Ku分别为对辊电机的控制输入电流和扭矩常数；Jd，Rd分别为对辊的转动惯量和半径，两者均为常量。式（7）可变换为

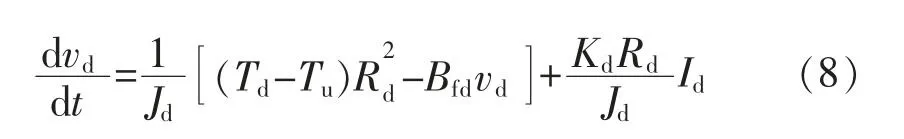
对于放卷辊，基板张力Tu对其产生正向力矩，驱动电机对其产生反向力矩，由力矩平衡方程得：

式中：Bfu为放卷辊的轴承粘滞摩擦系数；Iu，Ku分别为放卷电机的控制输入电流和扭矩常数；Ju，Ru分别为放卷辊的转动惯量和料卷卷径，两者为变量，随放卷过程不断变小。

放卷辊每旋转一圈，其卷径变化量为单层基板厚度h，在Δt时间内，若放卷辊的卷径变化为ΔRu，则放卷辊的旋转圈数为

令时间Δt 趋于零，由式可得：

放卷辊的转动惯量Ju由三部分组成，包括放卷电机的转动惯量Jmu，轴芯（气胀轴）的转动惯量Jcu，放料料卷的转动惯量Jeu。则Ju可表示为Ju=n2Jmu+Jcu+Jeu，其中nu为传动比。Jmu和Jcu均为常量，Jeu是变量，随卷径Ru变化。

料卷的转动惯量Jeu可表述为

式中：W为基板宽度，Rc为放卷辊的轴芯半径。

将式（12）代入Ju，对Ju求导，得：

联立式（9）、式（11）和式（13），求得放卷辊的速度方程如下：

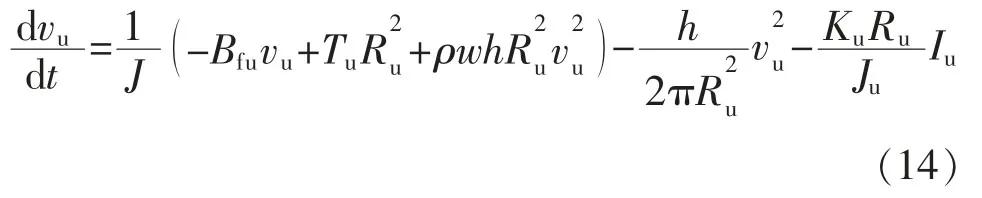
式（6），式（8）和式（14）共同构成了放卷系统的基板张力和速度模型。

2 放卷张力的模糊PID控制器设计

放卷系统中对辊提供参考速度，通过调节放卷辊来控制放卷张力，因此在控制模式上将放卷辊设为张力模式，对辊设为速度模式。为了提高响应速度和抗干扰性能，将放卷辊设计为串级张力闭环控制，如图3所示。其中主回路为张力控制，副回路为速度控制。针对时变卷径和速度扰动问题，将主回路中的张力控制器设计为模糊PID控制器。

2.1 模糊PID控制的基本原理

图3 放卷系统控制结构图Fig.3 Control structure diagram of the unwinding system

模糊PID的控制结构图如图4所示。模糊PID控制器主要包含两部分，一部分是模糊控制器，采用双输入三输出的控制结构，偏差e 和偏差变化率ec为输入，ΔKp、ΔKi、ΔKd为输出；另一部分是参数可调的PID控制器，其作用是根据模糊控制器的输出实时修正Kp、Ki、Kd 三个参数值。

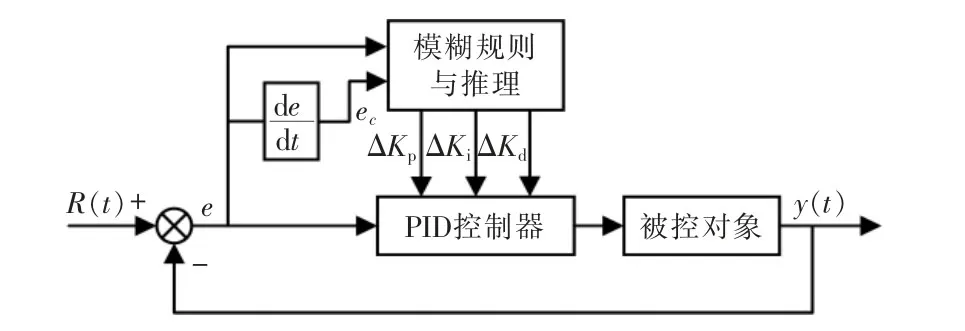
图4 模糊PID控制结构图Fig.4 Structure diagram of fuzzy PID control

模糊PID控制的基本原理就是系统将偏差e和偏差变化率ec输入模糊控制器，通过模糊量化、模糊规则与推理、反模糊化处理，实时计算出PID控制器三个参数的修正值，将修正后的精确控制量作用于被控对象。

2.2 模糊PID控制器设计

模糊PID控制器的设计步骤如下所示：

（1）选取张力偏差e 和其变化率ec作为模糊控制器的输入变量，PID 参数修正量ΔKp、ΔKi、ΔKd作为模糊控制器的输出变量。将输入输出变量进行模糊化，设定模糊语言集为7个，即｛NB，NM，NS，ZE，PS，PM，PB｝，对应的含义为｛负大，负中，负小，零，正小，正中，正大｝。

（2）结合实验数据分析和张力控制系统特性，建立输入变量e、ec和输出变量ΔKp、ΔKi、ΔKd的隶属函数。各变量的隶属度函数相互独立，通过模糊控制规则相关联。根据所设定的模糊论域，输入输出变量选取相同的隶属函数，因此以变量ΔKi为例，其隶属度函数曲线如图5所示。

图5 ΔKi 隶属函数曲线Fig.5 Membership function curve of ΔKi

（3）根据PID 参数对系统输出特性的影响，可归纳出不同偏差和偏差变化率对于被控系统的作用。结合实验和专家经验可知，当偏差较大时，为了加快系统响应速度，应取较大ΔKp和较小ΔKd。另外为避免系统响应出现较大的超调，通常取ΔKi=0。当偏差和变化率为中等大小时，ΔKp应取较小，ΔKd，ΔKi取值应适当。当偏差较小时，应增大ΔKp、ΔKi值，适当选取ΔKd。根据以上原则，建立模糊规则表，7个语言变量对应49条模糊规则，ΔKp、ΔKi、ΔKd模糊规则如表1、表2和表3所示。

表1 ΔKp 模糊控制表Tab.1 Fuzzy rule of ΔKp

表2 ΔKi 模糊控制表Tab.2 Fuzzy rule of ΔKi

表3 ΔKd 模糊控制表Tab.3 Fuzzy rule of ΔKd

3 仿真分析

由图3所示的放卷系统控制结构图，结合放卷系统的基板张力和速度模型，建立如图6所示的放卷系统的张力和速度仿真框图，按图6 在Simulink中建立放卷系统的基板张力和速度的仿真模型。其中对辊为速度模式，放卷辊为张力模式，GTC（s），GSC1（s）分别为放卷辊的张力控制器和速度控制器，GSC2（s）为对辊的速度控制器，虚线框所示部分为基板的张力模型。GSC1（s）和GSC2（s）采用常规PID控制，GTC（s）分别采用常规PID 和模糊PID控制器进行对比实验。仿真采样时间设为10 ms，设定张力值Tref=30 N，Td=30 N，速度值Vref=0.5 m/s，料卷的初始卷径Ru0=0.2 m，基板宽度W=0.2 m，基板厚度h=50 μm，杨氏模量E=3 GPa。

图6 放卷系统的仿真结构图Fig.6 Simulation block diagram of tension and velocity

图7所示为放卷张力的阶跃响应曲线。由图7可知，相比PID控制，模糊PID控制时张力超调量明显减小，超调量由20%降到8.3%，性能好于PID控制。模糊PID的张力响应速度略慢于PID控制，上升时间延迟了约0.15 s，调节时间并无明显差异，满足放卷系统张力控制的要求。

图7 基板张力的阶跃响曲线Fig.7 Step response curve of the web tension

图8所示为放卷系统的给定张力值发生连续阶跃变化时的响应曲线。由图8可知，在张力给定值连续变化时，PID控制和模糊PID控制均能较好地跟踪放卷张力的变化，模糊PID控制的张力超调量明显减小，但张力响应速度变慢，上升时间和调节时间都有所增加。

图8 张力给定值变化时的响应曲线Fig.8 Response curve with the reference tension value varying

在料卷半径为Ru0和Ru0/2时分别采用PID控制、模糊PID控制来测试放卷张力的波动变化，仿真结果如图9所示。常规PID控制在Ru0/2时超调量相比Ru0时减少5%，但调节时间增加0.4 s，而模糊PID 在Ru0和Ru0/2 下张力响应无明显变化。仿真结果说明模糊PID控制张力的鲁棒性更好。

图9 不同料卷半径下的张力响应曲线Fig.9 Response curve of the web tension with different radius of unwinding roll

保持张力设定值30 N 不变，改变对辊轴速度，初始速度设定为0.5 m/s，在第2 s时增加至1 m/s，在4 s时增加至1.5 m/s，在6 s时减少至1 m/s，上述速度突变情况下的放卷张力响应曲线如图10所示。由图10可知，速度突变时放卷张力波动较大，PID控制时超调量达83%，模糊PID控制时超调量减小至43%，调节时间由1 s 减小到0.3 s。模糊PID控制放卷张力时具有良好的抗干扰性能。

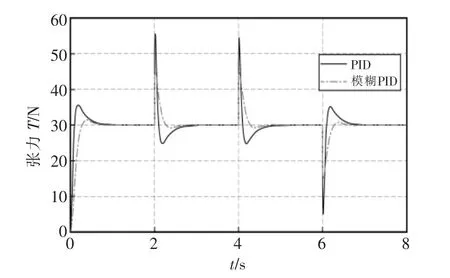
图10 速度扰动时的张力响应曲线Fig.10 Response curve of the web tension under step variation of the web velocity

4 结语

柔性膜放卷系统的时变卷径和速度扰动是放卷张力控制中的难题，本文研究了放卷系统的基板动力学，建立了放卷张力和速度模型。设计了放卷辊和对辊的控制模式，将模糊PID控制应用于放卷辊的串级张力控制回路，通过论域和隶属函数选择，建立了张力偏差、偏差变化率与PID 参数修正值相对应的模糊规则表，完成了仿真验证。仿真结果表明，模糊PID 张力控制器的控制精度高，超调量小，对时变卷径的鲁棒性好，且能有效抑制速度扰动时的张力波动。