基于ANSYS的某湖堤渗流场模拟分析研究
加勒尼
(新疆伊犁河流域开发建设管理局,乌鲁木齐 830000)
1 概 述
近几年,我国经济社会稳步发展,人民对美好生活的向往促使在某些地区兴起造湖。而江河湖海对堤坝稳定性要求较高,作为水利工程,堤坝稳定性又与自身渗流场表现息息相关。目前,有较多学者开展过针对海堤、河堤等渗流场研究,主要采用工程监测、数值模拟分析等手段[1-3],获得了比较丰富的研究成果。针对湖堤研究成果还主要应用相关河堤土石坝或者海堤设计规范[4-5],由于湖堤有其自身特殊性,因而开展湖堤渗流场研究具有十分重要意义。结合工程长期监测与数值模拟计算,评价湖堤渗流场表现[6],为湖堤渗流场稳定性评价研究提供重要参考。
2 渗流原理与ANSYS有限元分析
在水工建筑物中,需要考虑流体运动对人工建筑物的稳定性影响,而渗流即代表了流体运动形态,研究水工建筑物中流体的渗流特性常常利用有限元方法,本文将简要介绍渗流场原理与ANSYS有限元分析。
2.1 渗流原理
一维水流状态下的达西定律见式(1),表现了渗流量与流速及水头之间的理论关系[7]:
(1)
式中:U、k为达西定律的流量与渗透系数;H为渗流长度;A为截面积。
将一维达西定律推广至三维渗流场中,可得式(2):
(2)
式中:vx/kx、vy/ky、vz/kz为各渗流方向上速度与系数。
根据土力学固结原理与水力学质量守恒定律,可知地下水运动连续性方程为[8-9]:
(3)
式中:ρ为水流密度;λ为孔隙率;t为时间;V为单元网格体积。
以三维达西定律表述水运动连续性方程,并假定流体不可压缩,可得到:
(4)
针对二维介质材料,上式可简化成:
(5)
同样,针对流体介质饱和与非饱和状态,渗流方程演变为:
(6)
其中f(H)=B(H)+φCs
式中:B(H)为比水容量;φ为饱和系数;Cs为存流量,理想状态下,Cs为0。
故而渗流场分析转变成对上式及三维达西定律式的求解,而上式流体渗流方程的求解可依据工程实际边界条件,包括水头边界条件、流量边界条件、工程初始运营状态条件等。
另一方面,影响水工建筑物渗流场的一个很重要外在因素即是降雨。降低水利枢纽工程抗滑稳定性,建筑物基础底板渗透压力增加,这些均会在一定程度上加速水工建筑物中渗流场运动,故而本文将特别介绍降雨入渗影响。
在前人研究基础上,以式(7)为评判降雨入渗程度,其中降雨最强入渗能力Rmax以河流湖中浸润线与水利枢纽工程溢出点高程超过地面的临界降雨强度为标准。
(7)
式中:Rmax为降雨入渗峰值;h为水头;N(h)为不同水头下降雨入渗程度。
2.2 ANSYS有限元分析
有限元分析主要集中在数学泛函数的求解,从ANSYS插值分析原理入手,划分有限单元节点,类比ANSYS温度场分析模块式(8),解决式(9)渗流分析解。
(8)
式中:ηx、ηy为温度系数;bT为比热系数;Q为热能转化率。
(9)
(10)
以水流自由活动面和溢出点作为饱和与非饱和区域,确定降雨入渗最大量,以有限元单元网格为计算单元,逐一循环计算,以控制方程为收敛评判标准,直至渗流场得到收敛,从而获得稳定与非稳定渗流场分布结果。
3 工程概况
本文研究对象为我国东部某地区南向区段湖堤,人工湖库容量达100×104m3,常年受台风侵扰及水流冲刷作用,堤坝稳定性受到严峻挑战。地质勘察资料表明,堤坝所属区域为冲积平原,上覆土层主要为第四系沉积黏土与褐色砂土层,厚度达4.5 m,表层分布为砂质粉土,土体透水性属弱透水性能。湖堤管理部门定期对堤坝清基处理,增强堤坝抗滑稳定性。湖堤平均海拔为6.87 m,抗震设防烈度为Ⅴ度,采用钢筋混凝土浇筑制作,堤坝基础为筏型基础,堤坝顶面高度约7.5 m,堤身坡度为1.2%,迎水侧采用抗冲刷材料堤身,内外侧坡度一致,堤坝顶设置有防洪墙。调查发现,在降雨季节,堤坝表面孔洞渗水明显。水文监测表明,该人工湖水位受入口河流影响,每日水位均会出现一定涨幅变化,最高水位可达4.5 m,水位变化幅度最大至1.4 m,探讨其内部渗流场变化对水文观测及评价堤坝稳定性具有十分重要作用。
4 基于ANSYS的堤坝渗流场模拟分析
以PLANE55为单元网格类型,根据南向区段堤坝尺寸划分网格,并对渗流场监测孔单元网格加密划分,见图1(a)。考虑水头边界条件与流量边界条件,以背水侧水头2.55 m作为水头边界条件,由于土层弱透水性,设定地基土层与基础之间为不透水层,断面处流量边界设置为零,施加边界条件后数值模型见图1(b)。
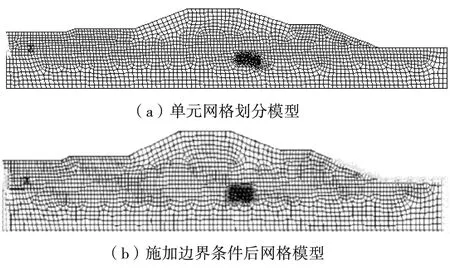
图1 建立网格模型
4.1 稳定渗流分析
图2为计算获得的堤坝稳定渗流场孔隙压力云图(以水头表示)。从图2中可看出,稳定渗流场中存在堤坝吸力水头,出现在坝顶,最大吸力水头达4.625 m,沿着坝顶至坝基,孔隙水压力逐渐增大,在坝基处最大孔隙水压力达到峰值,达9.6 m,坝身孔隙水压力水头平均值为7.8 m,低于坝身混凝土抗压强度,表明该湖堤稳定渗流场处于安全运营区间。
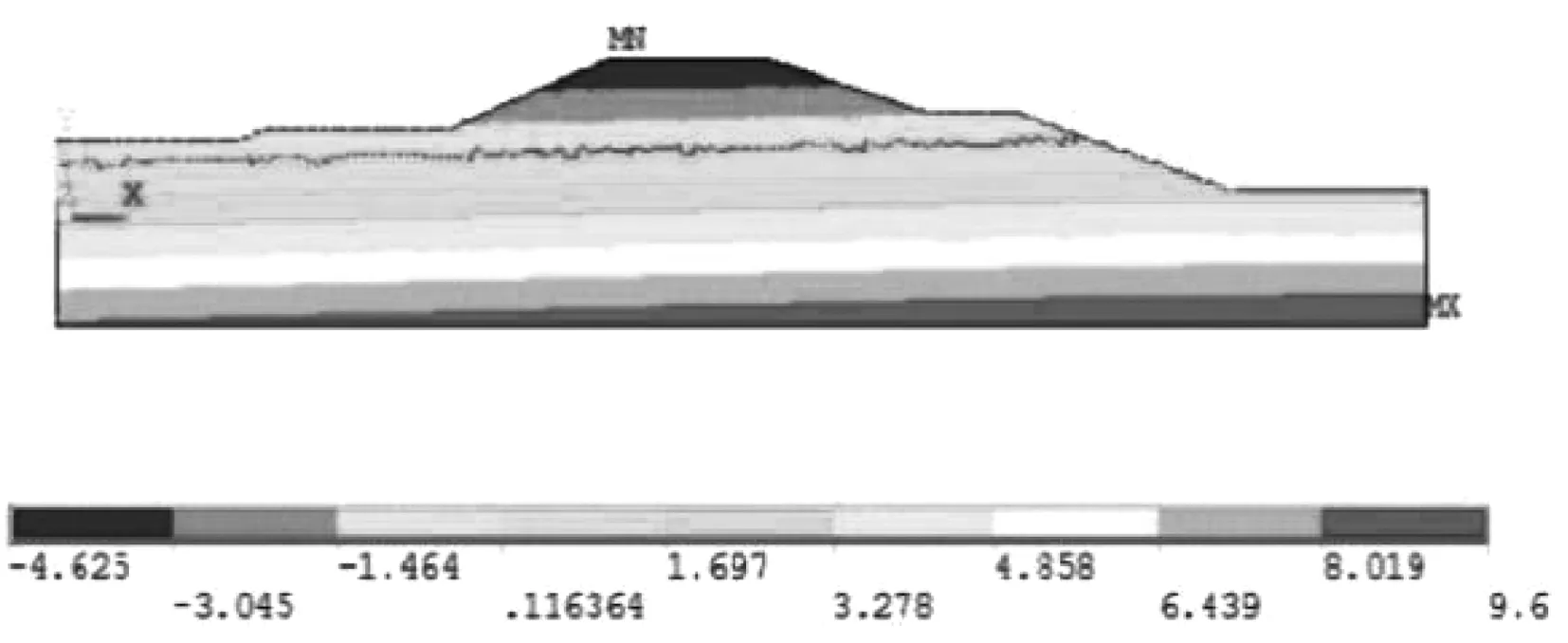
图2 稳定渗流场孔隙压力云图
4.2 降雨影响渗流场分析
4.2.1 降雨与非降雨工况下渗流场特征
图3为未降雨工况与降雨强度为0.35 mm/min条件下渗流场湖堤孔隙水压力云图。在未降雨工况下,堤身处于干燥状态,吸力水头最大为4.495 m,相比稳定渗流场,未降雨工况是非渗流场,由于湖堤迎水侧水位发生变化幅度明显,故而湖堤实质上受到的均是非稳定渗流状态。当降雨强度达到0.35 mm/min时,湖堤内最大吸力水头增大17.2%,渗流场活跃度增大,表明降雨强度会影响湖堤渗流场分布。

图3 渗流场湖堤孔隙水压力云图
为了研究降雨强度对渗流场影响特征,需要确定最大降雨强度Rmax,通过确定湖内平均水位,不断更改渗流量的边界载荷,使有限元渗流方程模型达到收敛值。根据测算值,当降雨强度达到0.73 mm/min时,此时最大吸力水头达到5.3 m。依据运算过程确定降雨入渗强度曲线,见图4。依据有限元模型中吸力水头,反演出降雨强度,进而确定降雨强度与流量边界条件,以实际流量边界条件计算渗流场,从而确定降雨强度对渗流场影响程度。
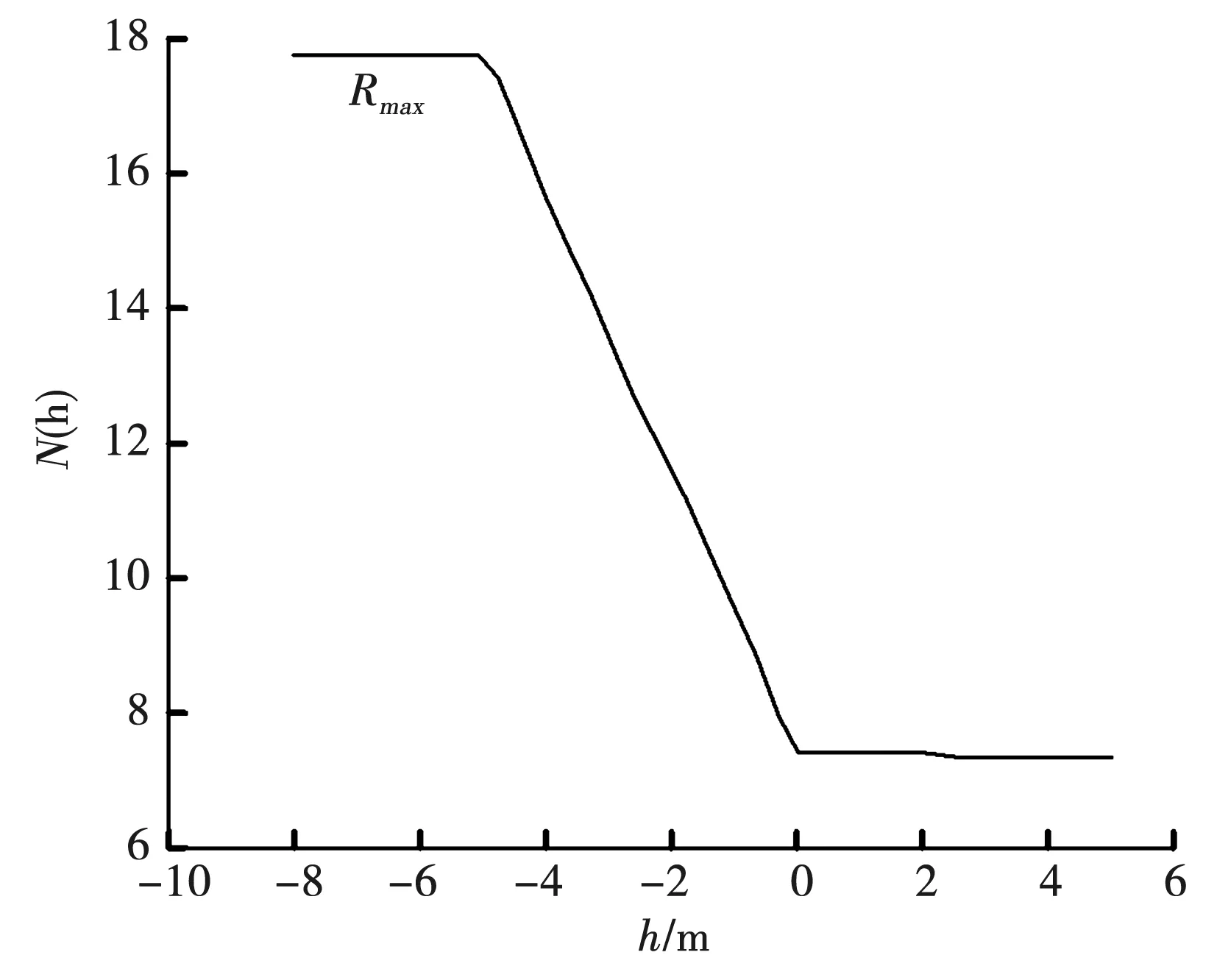
图4 降雨入渗强度曲线
4.2.2 降雨入渗与非入渗工况对比分析
为对比降雨入渗与非入渗工况下渗流场特征,以湖堤内传感器所测渗压为比较参数,对比两种工况下实测渗压值与有限元模型拟合值,见图5。从图5中可知,考虑入渗条件下相对误差最大值为5.3%,平均误差为1.44%,而降雨非入渗工况下最大相对误差亦仅只有7.45%,表明两种工况条件下有限元模型渗流方程解满足要求。从入渗是否两工况渗压解来看,降雨量为1.41 mm/min时,考虑入渗影响下有限元模型渗压为2.74 m;而非入渗条件下为2.85,相比入渗条件下,非入渗相对误差更大。

图5 实测渗压值与有限元模型拟合值对比
为了对比考虑降雨是否入渗对渗流场的影响,引入离差理论[10],计算获得湖堤在一定时间段内降雨入渗与非入渗离差变化曲线(图6)。从图6中可知,在未发生降雨条件下,离差值为0,表明降雨入渗与非入渗结果是一致;当在第8.3 h发生降雨,而从第9.7 h至14.86 h离差值增大,此后离差值仍维持在0.01 m,持续时长达8.6 h,从第40.54 h开始,离差值稳步提升,降雨量减弱,离差值稍会降低;在第62.6 h后,湖堤区段未再有降雨情况,离差值逐渐阶梯式下降,直至第120 h,离差值才趋于0,从最后一次降雨至离差值为0,持续时长达57.4 h。由上述分析可知,降雨入渗对湖堤渗流场确有影响,且影响滞后于降雨出现时期;另一方面降雨入渗相比更符合实际降雨工况对湖堤渗流场影响。
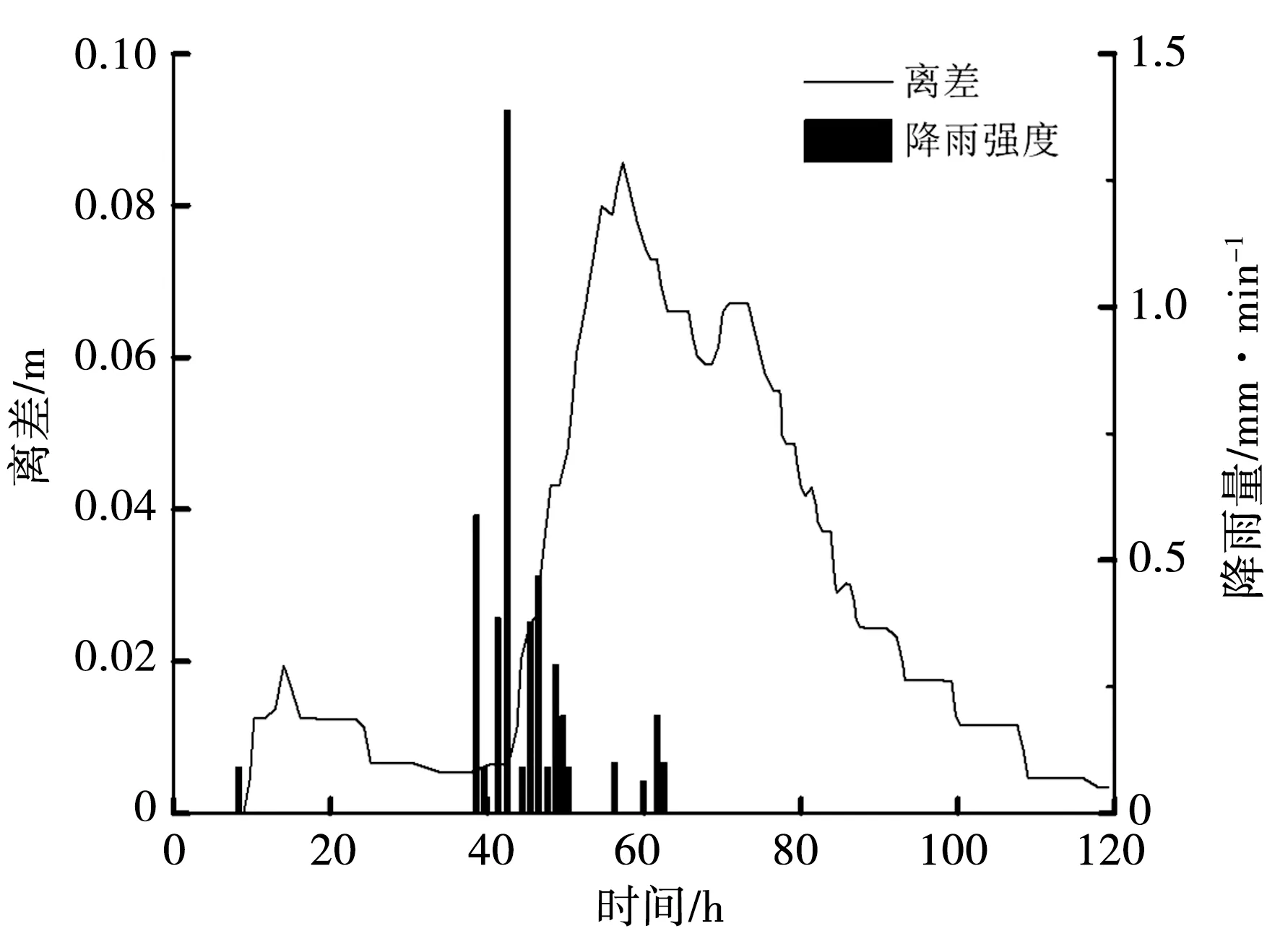
图6 降雨入渗与非入渗离差变化曲线
4.3 初始边界条件影响有限元结果特征
迎水侧不同水位条件下,渗流场模拟结果会有所差异,以湖堤内不同初始水位条件为研究目标,分别获得对应的渗压变化曲线。为对比分析,本文选用的4个初始水位分别为峰值水位、下降水位期、谷值水位、上升水位期,分别模拟各条件下渗流场(图7),获得渗流模拟变化曲线。
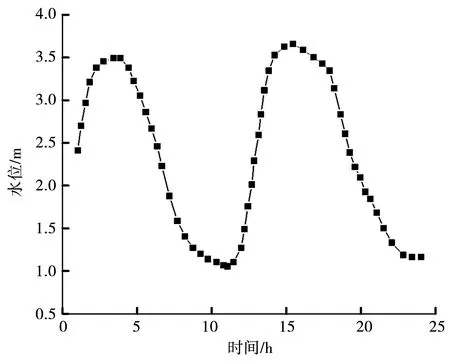
图7 初始水位示意图
图8分别为4种初始水位条件下渗流模拟结果。从整体表现来看,无论初始水位处于何种状态,渗流场模拟结果与实际结果在初期阶段总是存在一定差距,直至某个时间阶段,模拟结果才趋于收敛,峰值水位与谷值水位需要35 h,而上升或下降水位期间15~20 h,表明初始水位以平均值更易达到模拟结果收敛。

图8 渗流模拟结果
图9为4种工况条件下在典型区间段内的相对误差值变化曲线。从整体表现来看,4个初始水位均是随着时间推移,相对误差值逐渐减小,并最终均趋于收敛至3%。从相对误差变化幅度来看,下降水位期相对误差仅有54%波动,各个阶段内相对误差较稳定,表明渗流模拟结果较优;谷值水位变化幅度较大,该工况下最大相对误差比最小相对误差要高319%;峰值水位、谷值水位、上升期水位、下降期水位平均相对误差分别为11.4%、6.87%、4.1%和1.95%,结合相对误差表现来看,湖堤渗流场模拟结果初始水位已下降期平均水位表现较好,更能较快获得渗流收敛值。

图9 相对误差值变化曲线
5 结 论
以某湖堤为工程对象,利用ANSYS有限元数值分析平台,分析该湖堤渗流场模拟结果表现,结论如下:
1) 堤坝稳定渗流场中存在吸力水头,集中在坝顶面,最大吸力水头达4.625 m,坝身孔隙水压力水头平均值为7.8 m,坝基处孔隙水头压力最大,达9.6 m。
2) 降雨强度增大,吸力水头增大,渗流场活跃度增大,降雨强度影响初始流量边界条件。
3) 得到降雨入渗与非入渗两种工况下离差值,未有降雨两种工况模拟结果一致,当降雨量增大,离差值增大,且离差值表现总滞后于降雨期,降雨影响持续时长达57.4 h,后趋于收敛平静。
4) 以下降期水位为初始边界条件的模拟结果相对误差更小,相比峰值水位、谷值水位及上升期水位3种边界条件,长历时变化更稳定,仅有54%波动,渗流模拟结果更快收敛。

