基于改进粒子滤波的未知放射源定位方法

刘浩杰，肖宇峰,*，张 华，田星皓，张 秤

(1.西南科技大学 特殊环境机器人技术四川省重点实验室，四川 绵阳 621000；2.中国原子能科学研究院 核技术应用研究所，北京 102413)

核技术的发展已走过了100多年的历程，在国防现代化建设、工业、农业、生命科学、材料科学、信息科学、环境保护和人民健康等方面发挥着重要作用，但因为监管不当导致的放射源丢失也给人类生产和生活带来巨大威胁。

放射性物质的丢失将带来大场景下搜寻未知放射源的困难，准确、有效地确定其位置是开展应急处置工作的首要条件。针对放射源的定位问题，国内外都展开了相应的研究，主要方法分为固定式探测和移动式探测两类。固定式探测又分为单点探测和多点探测。单点探测主要围绕射线检测研发各类探测仪器，已有大量研发成果和产品，适合区域较小、放射性分布较明确的场景，如三角圆筒铅屏蔽的NaI探测器[1]、NaI(Tl)晶体探测器[2]、高纯锗探测器[3]、厚GEM探测器[4]等。多点探测通过部署传感器网络来发现放射源，大量的探测结点带来高额的维护成本，且放射源的定位误差也较大[5-7]。移动式探测通过移动平台搭载辐射计数器来发现放射源，这类研究较新颖且实用价值较高，主要问题是需要人工遥控平台探测、定位放射源，而且在大场景下探测未知源时效率低下[8-9]。综合来看，固定式探测的准确性受测量位置和测量区域的约束，不适合大场景下的未知源搜寻。相比之下，移动式探测不受测量位置和区域的限制，具有很好的灵活性。

针对移动式探测遇到的大场景下未知源探测效率低下问题，本文提出一种可应用于自主移动机器人上的放射源定位方法：在递推贝叶斯估计模型上，通过改进的粒子滤波器融合机器人自定位数据和辐射计数值，进而估计放射源位置和放射性活度。

1 放射源定位参数估计模型

1.1 放射源定位

假设某区域内存在1个位置和放射性活度均未知的放射性点源(忽略尺寸大小)，为简单起见，只考虑二维平面区域而不计放射源的垂直高度。为估计这个未知放射源的位置和放射性活度，利用自主定位的移动机器人搭载辐射计数器进行移动探测，如图1所示，进而根据探测信息实现放射源定位。向量gk=[xk,yk,zk]T表示在该平面某位置(xk,yk)的1个观测点，zk为观测点处的辐射计数。其中k∈N*(N*为正整数集)，表示不同的观测点。用X=[xs,ys,As]T表示放射源参数向量，(xs,ys)为放射源的平面坐标，As为放射源的活度。

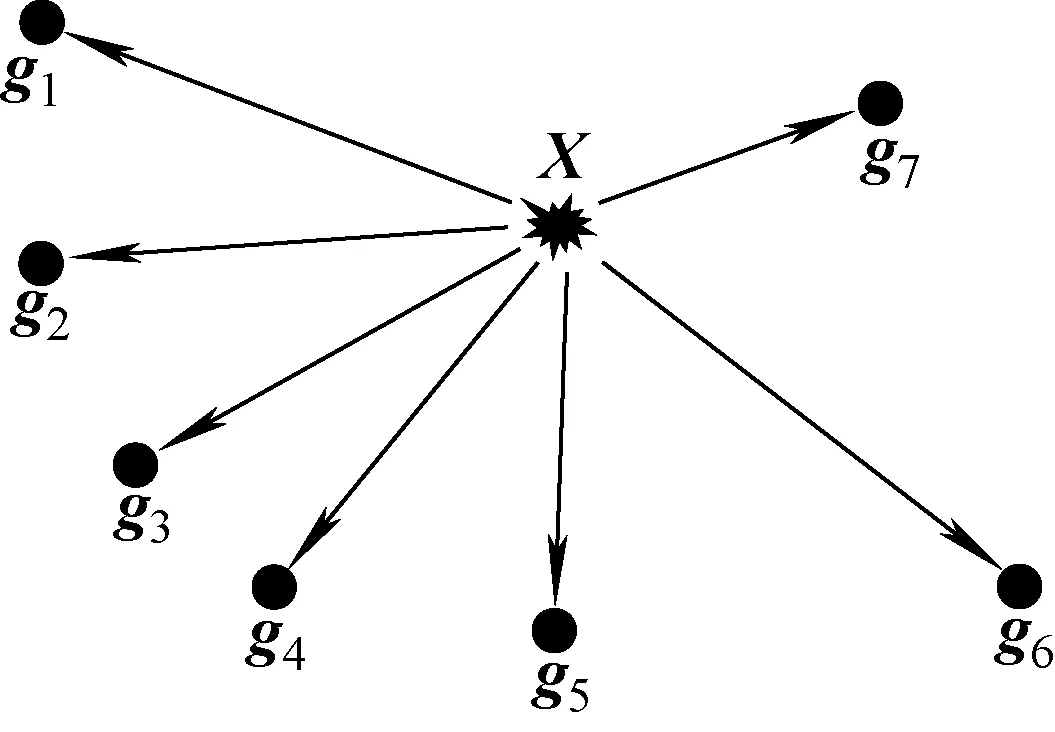
图1 放射源检测示意图Fig.1 Schematic diagram of radioactive source detection

已有研究[10-11]证明，核衰变过程中辐射计数器中的计数值服从泊松分布，假如某个位置处的辐射计数率为μ，则辐射计数器在τ时间内检测到计数值为z∈N(N为自然数集)的概率P(z;λ)为：

(1)

式中，λ=μτ为泊松分布的均值，且其方差σ2=λ。

如果在观测位置(xk,yk)用辐射计数器测量一段时间(τk)得到计数值zk，则zk的似然函数为：

P(zk|X)=P(zk;λk(X))

(2)

式中：P(zk|X)为式(1)定义的泊松分布；λk(X)为平均辐射计数值，若放射源的活度为As，且每次衰变只发出1个光子，光子发射率为100%，则λk(X)可近似表示为：

(3)

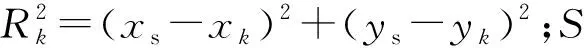
1.2 递推贝叶斯估计在放射源参数估计中的应用

在信号处理领域，递推贝叶斯估计方法可利用带有噪声的观测信息来最优地估计系统的状态或参数，即每接收1个新的观测信息，都会递归地更新系统状态的后验概率密度函数，根据这个函数即可得出系统状态的最优估计。设放射源参数向量X=[xs,ys,As]T在经过第k-1次测量值的处理后得到后验分布P(X|z1:k-1)，其中z1:k-1={z1,…,zk-1}为测量值的累积集，当接收到第k次测量值zk时，后验分布更新为P(X|z1:k)，即：

(4)

式中：P(zk|X)为式(2)定义的似然函数；P(zk|z1:k-1)为归一化常数。利用更新后的后验分布可估计放射源的位置和放射性活度。

2 基于改进粒子滤波的放射源定位算法

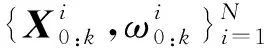
在滤波过程中，为避免因递推次数增加而造成样本退化现象，一般需进行重采样，但由于传统重采样只复制少数高权值粒子而舍弃多数低权值粒子，易造成粒子多样性缺失。本文提出改进算法，即高权值粒子的放射源参数值由满足某正态分布的随机数代替，通过该算法可增加粒子的多样性、提高定位精度。基于改进粒子滤波算法估计放射源参数的主要过程包括粒子初始化、权值更新与归一化、自优化重采样、放射源参数估计。

2.1 粒子初始化

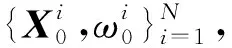
(5)

式中：U为均匀分布；(xmin,xmax)、(ymin,ymax)分别为搜索区域横向与纵向的搜索范围；(Amin,Amax)为粒子放射性活度的范围。

2.2 权值更新与归一化

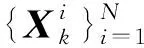
(6)

然后，将新的权值进行归一化：

(7)

2.3 自优化重采样

在粒子滤波过程中，不可避免地会出现样本退化现象，即随着递推计算次数的增加，粒子权值的方差会增大，具体表现为极少数粒子的权值很大，而大多数粒子的权值几乎为0，从而导致大量的计算浪费在无用粒子的更新上。为解决样本退化问题，目前最常用的方法是重采样，其核心思想是保持粒子总数不变的情况下，淘汰权值小的粒子，保留并复制权值大的粒子。

在重采样前，为确定粒子退化程度，引入有效样本数Neff，Neff可用下式近似估计：

(8)

当有效样本数Neff小于阈值Nthr时进行重采样，否则保持粒子不变。文献[12]实验证明，当阈值Nthr设置为2N/3时(N为粒子总数)，效果最佳。

在精确度方面，由于系统重采样的估计误差最小[13-15]，所以选择系统重采样(SR)算法解决样本退化问题，其主要过程如下：

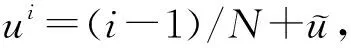
虽然重采样算法对样本退化问题有一定的抑制作用，但随着重采样次数的增加，由于只复制高权值粒子，将导致样本多样性的缺失。为克服样本多样性匮乏问题，采用优化高权值粒子的改进重采样算法——自优化重采样(A-SR)算法，具体过程如下。

步骤1，首先根据粒子的权值判断有效样本Neff是否小于阈值Nthr，如果满足条件，则利用SR算法对粒子进行筛选和复制，否则保持原来的粒子集。

步骤2，考虑到步骤1中可能导致多样性缺失，对复制的高权值粒子进行以下优化：

(9)

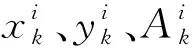
考虑到随着迭代次数的增加，粒子集会越来越收敛，活动范围缩小，所以影响粒子波动的方差应随观测次数k(即迭代次数)的增加而减小。合适的σp与σr能增加粒子的多样性，使对放射源位置和活度估计的精确度得到一定的提高，因此它们的选值是改善粒子滤波算法结果的关键。

2.4 放射源参数估计

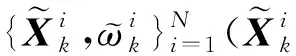
(10)

重复以上过程将使粒子不断地收敛，放射源的估计值也会逐渐向实际值靠拢，当粒子空间横向长度与纵向长度中的最大值小于或等于某个阈值Dthr时，即：

(11)

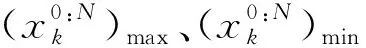
2.5 放射源定位算法实现步骤

在粒子滤波框架中，引入放射源定位参数值估计和自优化重采样思想，完成基于改进粒子滤波的放射源定位算法。算法步骤如下。

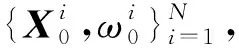
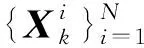
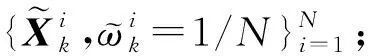
3 仿真实验与分析

为验证方法的准确性和有效性，在matlab软件下开展仿真实验，计算机采用intel(2.8 GHz)处理器，4 GB内存。实验过程如下：1) 在150 m×150 m平面区域内设置1个放射源；2) 假设移动机器人携带辐射计数器进入该区域，并探测所处位置点的辐射计数值；3) 执行改进粒子滤波算法，利用测量的位置坐标和辐射计数值更新粒子集，进而得到放射源位置和放射性活度的估计值；4) 对比分析放射源参数的设置值和估计值，评价估计方法的准确性和有效性。

3.1 重采样改进后的效果分析

设置1个放射性点源的位置坐标为(xs=85 m,ys=100 m)、放射性活度As=294 MBq。仿真实验参数设置如下：xmin=0 m、xmax=150 m、ymin=0 m、ymax=150 m、Amin=30 MBq、Amax=1 GBq，有效探测面积S=3.14×10-3m2，(本征)探测效率ρ=30%，本底辐射计数率nb=10 s-1，粒子个数N=5 000，每个观测点处辐射计数器的测量时间相等且满足τ=10 s。在搜寻放射源的过程中，每记录1个观测值都会通过滤波过程更新粒子集，并估计出放射源的位置和放射性活度，然后移动机器人向估计的放射源方向移动15 m到达新的观测位置，进行新一轮的测量和估计。

为突出重采样算法改进前后的差异，暂时不考虑屏蔽物的影响，分别采用SR算法和A-SR算法估计放射源，其粒子分布情况示于图2，横轴和纵轴分别表示二维平面中x方向和y方向上的位置坐标。由图2可看出，经过多次迭代估计，由于SR算法只筛选出高权值粒子进行复制，导致了多样性匮乏，这会使粒子集信息量大幅降低而影响估计精度。A-SR算法增加粒子多样性的效果显著，使粒子集更加稠密。

统计重采样改进前后的位置误差和放射性活度误差，结果示于图3。由图3可知，A-SR算法较SR算法的估计误差小，表明改进算法提高精度的效果显著。

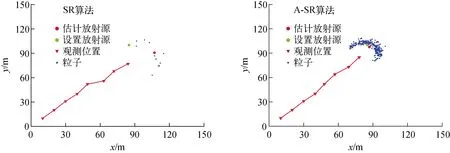
图2 SR算法和A-SR算法估计的放射源粒子分布Fig.2 Particle distribution by SR and A-SR method

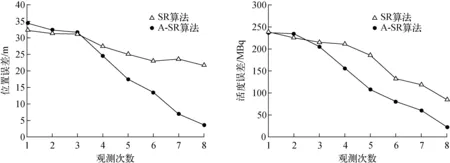
图3 重采样改进前后的位置误差和放射性活度误差分析Fig.3 Analysis of position error and radioactivity error before and after resampling improvement

通过以上对比实验分别得到了最佳σp和σr值。但当σp和σr同时取最佳值参与计算时，会因为过多地增加粒子的多样性而影响最后估计的精度，所以此时σp和σr的值应适当下调。经过大量实验对比发现，当σp=50且σr=45 MBq时，误差最小，为验证该结果，将σp=60且σr=0 Bq、σp=0且σr=50 MBq、σp=50且σr=45 MBq时估计的各项误差进行比较，结果示于图4e、f。由图4e、f可知，当σp=50且σr=45 MBq时，估计值与设置值的位置误差以及放射性活度误差均较小，且误差波动更平缓。以上仿真结果表明，当选取最佳σp和σr参数时，提高精度的效果最为显著。

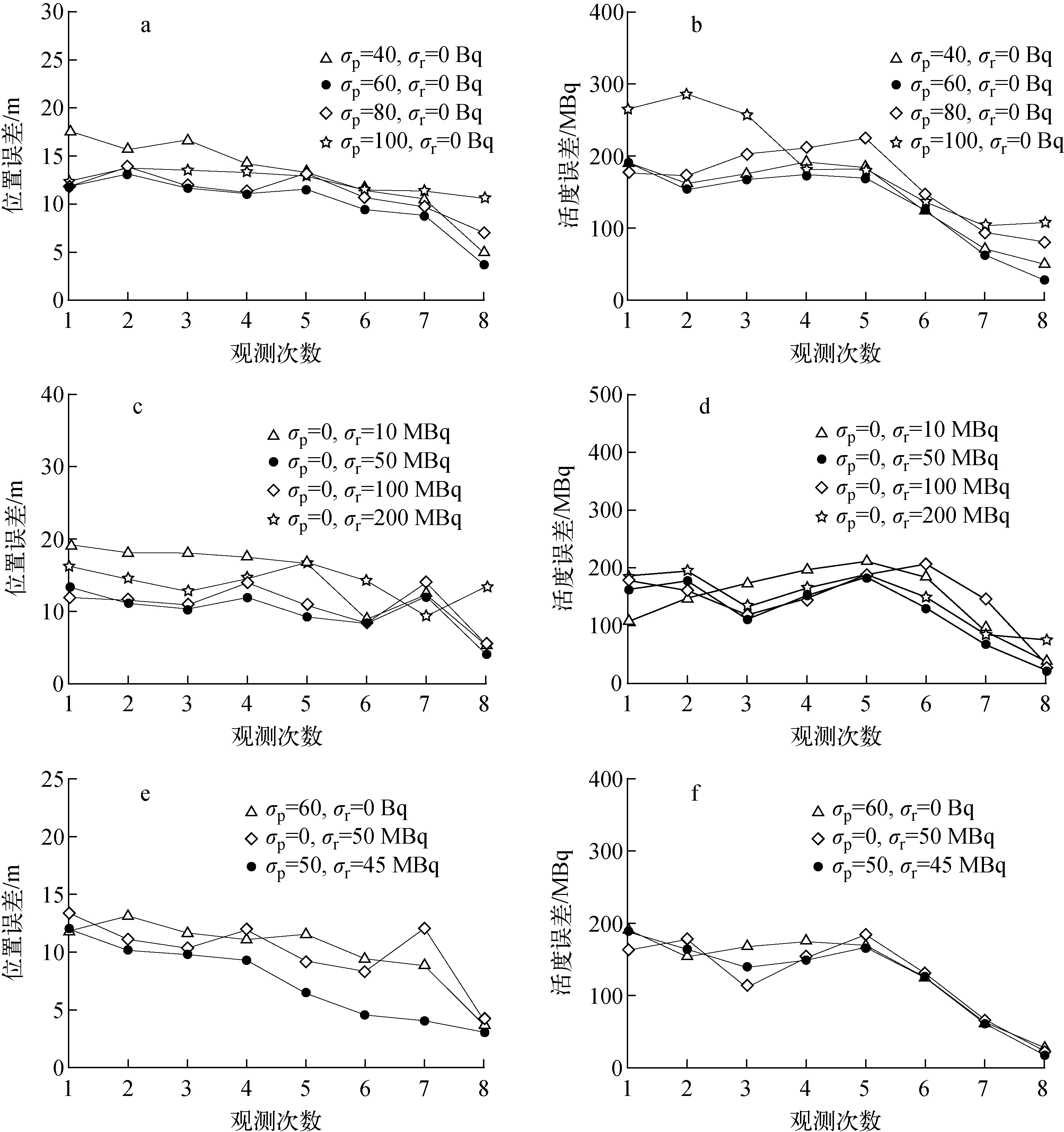
a——σp影响的位置误差；b——σp影响的放射性活度误差；c——σr影响的位置误差；d——σr影响的放射性活度误差；e——3种最佳情况下的位置误差对比；f——3种最佳情况下的放射性活度误差对比图4 σp和σr影响的各项误差对比分析Fig.4 Comparative analysis of error affected by σp and σr

3.2 有无屏蔽物干扰下定位的对比分析

为模拟无屏蔽物干扰情况下的放射源定位，假设1个放射性点源位置设置为(xs=40 m，ys=105 m)，放射性活度As=294 MBq，如图5所示，其余参数与3.1节相同。对于放射源的估计过程，主要分为2个阶段。阶段1：让搭载辐射计数器的可自主定位移动机器人从起点开始进行测量和估计(为验证算法的普适性，设置2个不同起点：起点1(10 m，10 m)和起点2(120 m，20 m))，在完成放射源估计后，移动机器人向估计源方向移动20 m到达新的观测位置，继续测量和估计，循序进行下去(图5a)。阶段2：当机器人与估计放射源之间距离小于20 m时，采取环绕估计源移动的方式获取其周围的测量数据，环绕的方向不定，每次移动10 m，直到粒子集满足条件：max_length≤Dthr=5 m，停止估计(图5b)。

在实际环境中，搜索区域一般存在屏蔽物的干扰，如图6所示，若其中黑色部分是由材质相同的混凝土组成的屏蔽物，则根据文献[16]可设其线衰减系数μ=0.05，这种情况下对放射源的估计与无屏蔽物干扰时的估计过程相同，只是增加了移动探测的避障操作。对比图5、6可发现，在2种不同环境中均能较准确地估计放射源的位置，但当存在屏蔽物干扰时放射源位置的估计误差相对较大。

图5、6是基于A-SR算法的粒子滤波器在2种不同环境中对单个未知放射源进行估计的情况，为达到对比2种算法定位效果的目的，再利用基于SR算法的粒子滤波器同样在2种环境中对未知放射源进行估计，统计以 (10 m，10 m)为起点进行估计时这2种算法在2种不同环境中的估计数据，包括估计平面位置及误差、估计放射性活度及误差，结果列于表1、2。

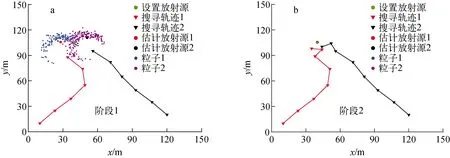
图5 无屏蔽物干扰下的放射源定位Fig.5 Location of radioactive source without shielding interference

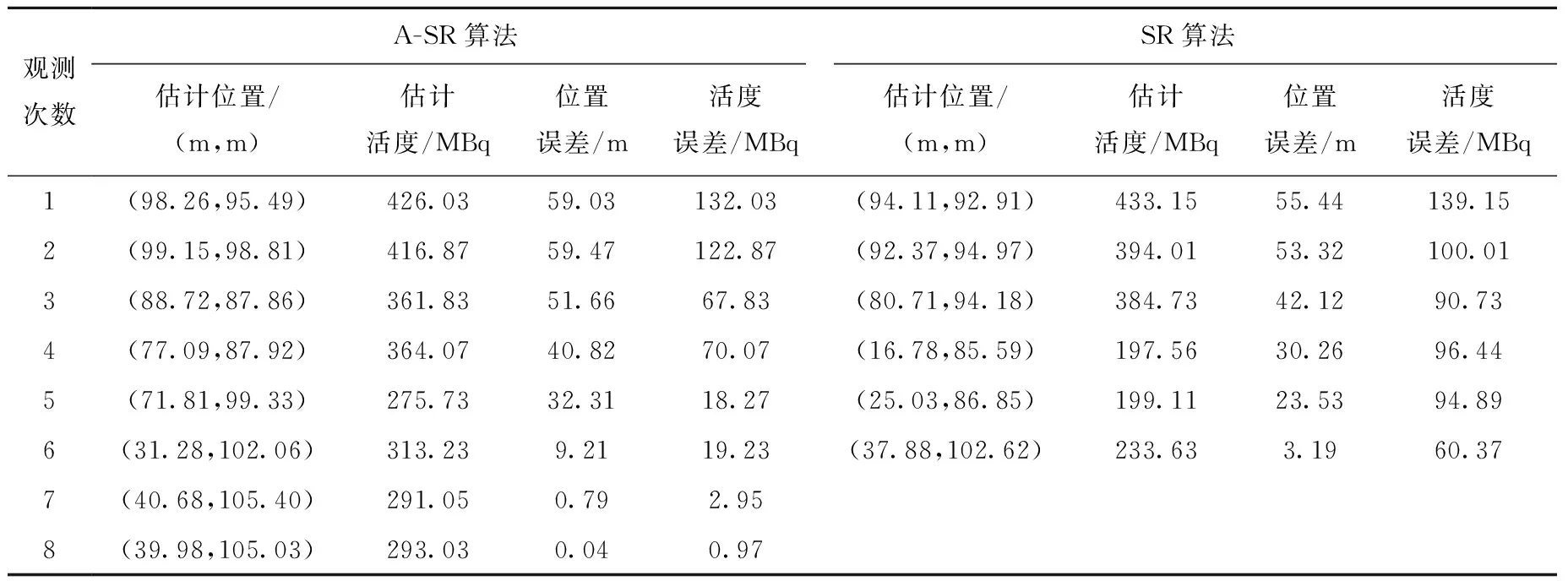
表1 150 m×150 m搜寻区域内无屏蔽物干扰时未知放射性点源的定位结果Table 1 Location result of unknown radioactive point source in 150 m×150 m search area without shielding interference

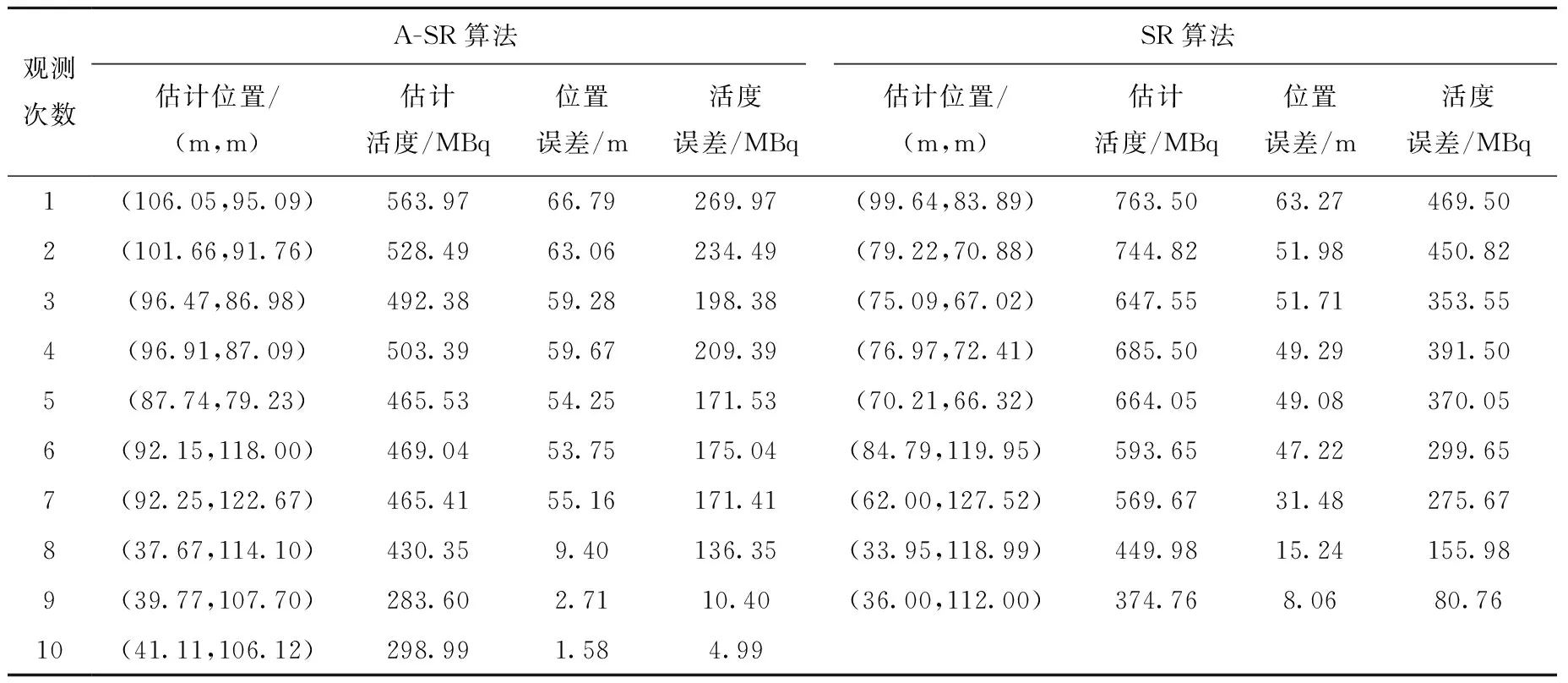
表2 150 m×150 m搜寻区域内存在屏蔽物干扰时未知放射性点源的定位结果Table 2 Location result of unknown radioactive point source in 150 m×150 m search area with shielding interference

由表1、2可知：1) 位置误差和活度误差表明A-SR算法提高了放射源的估计精度；2) 基于A-SR算法的粒子滤波器估计放射源时，在无屏蔽物干扰的环境中，位置误差达0.04 m，活度误差达0.97 MBq，在有屏蔽物干扰环境中，位置误差达1.58 m，活度误差达4.99 MBq，屏蔽物对放射源估计的结果影响很大；3) 有屏蔽物干扰情况下结束循序估计时的观测次数多于无屏蔽物干扰情况下的观测次数，同时，由于A-SR算法增加了粒子多样性，因此基于A-SR算法的粒子滤波器满足结束循序估计条件时的观测数较基于SR算法的粒子滤波器的观测次数多。

4 结论

针对在复杂环境中难以搜寻未知放射源的问题，提出一种基于改进粒子滤波的未知放射源定位方法，该方法结合辐射计数器和移动机器人提供的测量数据，在线估计单个未知放射源的参数，即位置和放射性活度。仿真实验结果表明此方法有效，在150 m×150 m搜寻区域中对未知放射性点源(活度设定为294 MBq)进行定位，无屏蔽物情况下位置定位误差约为0.04 m，放射性活度估计误差约为0.97 MBq；有屏蔽物情况下位置定位误差约为1.58 m，放射性活度估计误差约4.99 MBq。

实际应用中，放射源的数量和大小可能均未知，将来还需对本文方法做进一步优化。另外，可与辐射成像方法结合以提高定位精度，通过本文方法在较大范围内初步确定放射源，再利用辐射成像工具完成更精确的定位。