西安脉冲堆反应性引入事故瞬态安全特性分析

田晓艳，陈 森，杨 宁，朱 磊，李华琪，马腾跃，胡 攀，康小亚

(西北核技术研究院，陕西 西安 710024)

脉冲堆又称为TRIGA堆，可用于培训、研究和同位素生产，且能为抗辐射加固技术和核参数测量技术提供辐射模拟平台。西安脉冲堆(XAPR)是一座自然循环冷却池式研究堆，堆芯采用铀氢锆燃料，由于铀氢锆具有较大的瞬发温度负反馈系数，反应堆既可稳态运行，也可脉冲运行，其稳态运行额定功率为2 MW，脉冲运行额定功率为4 300 MW。稳态运行时堆内热量由冷却剂自然循环带到堆水池，堆池水温度则依靠一回路给水保持水温恒定，最终热阱为大气。尽管采用铀氢锆燃料的脉冲堆具有很好的固有安全特性，但若发生事故将对周围环境和人员安全产生较大影响，因此有必要研究脉冲堆在典型事故工况下的瞬态安全特性。到目前为止对脉冲堆的安全研究主要针对的是失水事故[1-2]，而对反应性引入事故的研究较少[3]。XAPR已运行多年，由于设备老化，发生控制棒失控弹出等反应性引入事故的概率增加，且可能发生安全棒卡棒导致反应堆无法实现紧急停堆。

为此，本文针对XAPR特有的堆芯结构和运行工况，建立适用于XAPR瞬态安全特性分析的数学物理模型，并基于吉尔算法自主开发瞬态安全分析程序TSAC-XAPR，研究XAPR在反应性引入事故下的安全特性，并为事故缓解提供参考依据。

1 物理模型与程序开发

XAPR采用自然循环冷却，即堆外池水通过冷却剂密度差产生的压力驱动流经堆芯，将堆芯产生的热量带出，堆池水温则依靠一回路强迫循环给水系统保持恒定。为提高计算效率，基于单通道模型，将堆芯简化为平均通道和热通道并联的模型，简化后的堆芯如图1所示。基于简化后的堆芯结构及堆芯参数建立了详细的物理模型，包括功率求解模型、换热模型、自然循环流量模型及空泡份额模型。

1.1 功率求解模型

堆芯功率由两部分组成：裂变功率和衰变功率。裂变功率采用具有6组缓发中子的点堆动力学模型求解，衰变功率采用保守的Glasstone关系式计算。反应性反馈包括燃料温度多普勒反馈、冷却剂温度反馈及冷却剂空泡反馈。

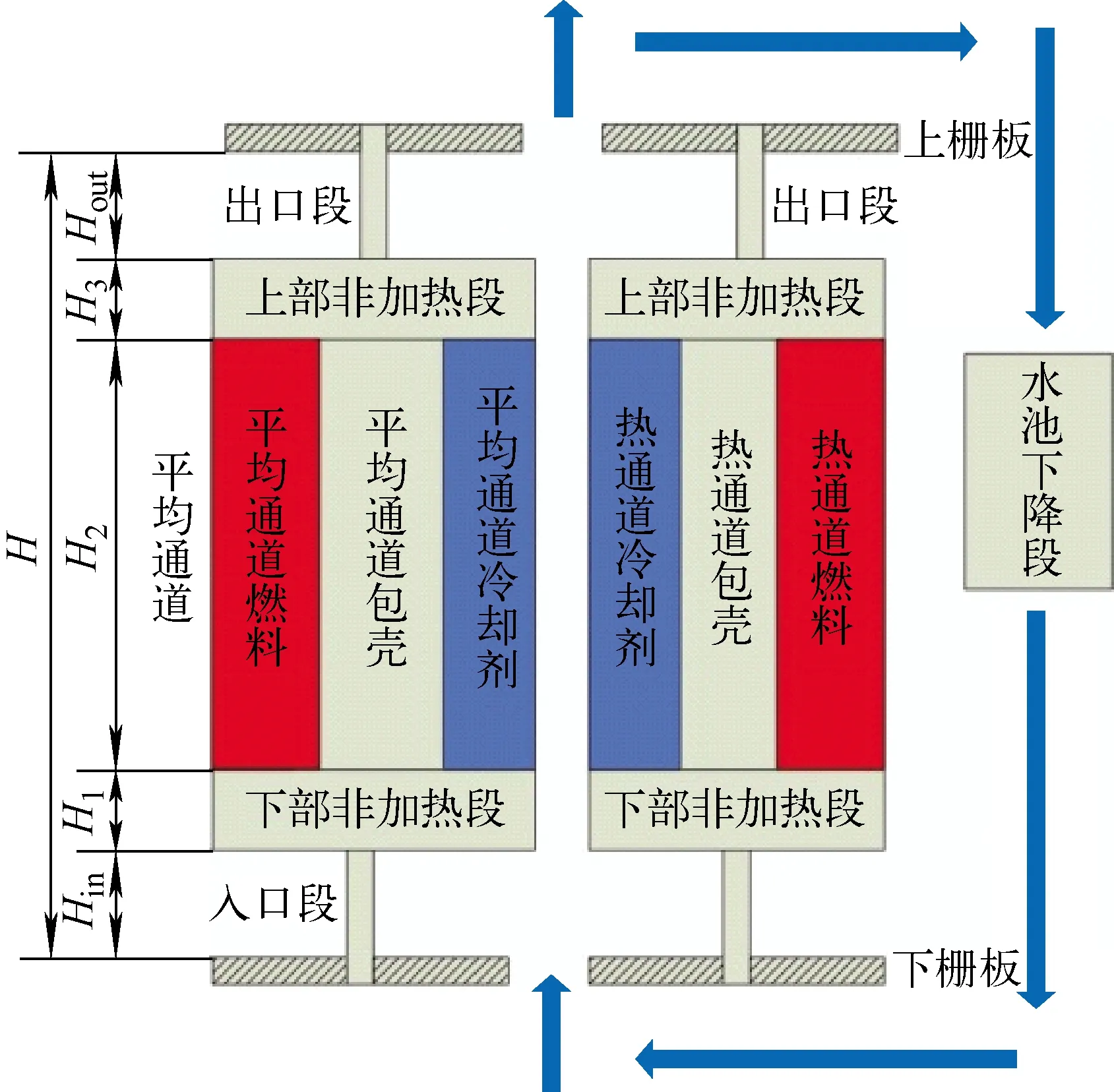
图1 XAPR简化堆芯示意图Fig.1 Simplified core schematic diagram of XAPR

Glasstone关系式[4]为：

0.87((t+2×107)-0.2-(t+t0+2×107)-0.2))

(1)

式中：Nβ，γ为停堆后的堆芯衰变功率，W；N0为停堆前的运行功率，W；t为停堆后的时间，s；t0为反应堆在功率水平N0的运行时间，s。

1.2 换热模型

冷却剂通道内的流型和换热模型将随反应性引入事故的进程而变化，建立相应于事故各阶段的换热模型，从而更准确地模拟事故动态行为。

1) 单相液体换热

根据堆内冷却剂流量可将单相换热模式分为池内单相自然对流换热和管内强迫对流换热以及二者之间的过渡换热。

(1) 池内单相自然对流换热

当堆内冷却剂流量接近于0时，堆芯换热模式为池内单相对流换热。

Nu=c(Gr·Pr)nGr/Re2≥10

(2)

式中：Nu为努塞尔数；Gr为格拉晓夫数；Pr为普朗特数；Re为雷诺数；c和n为常数，由实验确定，文献[5]给出其推荐值。

(2) 管内强迫对流换热

当冷却剂流量足够大时，堆芯内就形成了明显的宏观流动。根据Re流动又可进一步分为层流和紊流。本文采用的换热关系式分别为Sieder和Tate关系式与Gnielinski关系式[1]。

Re<2 300

(3)

Nu=0.012(Re0.87-280)·

(4)

式中：D为管道直径，m；L为管道长度，m；μ为动力黏度，Pa·s；下标l表示液相，w表示壁面。

(3) 过渡阶段混合对流换热

当冷却剂流量介于池内自然对流和管内强迫对流之间时，堆芯内同时存在宏观流动和微观流动。文献[5]建议混合对流换热关系式采用下式计算：

(5)

式中：NuM为混合对流努塞尔数；NuF和NuN分别为采用流动和池内自然对流关系式计算的努塞尔数，两种流动方向相同时取正号，相反时取负号，指数n通常取3。

2) 过冷沸腾

当包壳表面温度超过饱和沸腾温度而冷却剂还未达到饱和状态时可能会发生过冷沸腾现象。为计算过冷沸腾阶段的换热系数，需采用合适的关系式确定充分发展过冷沸腾起始点。本文采用Saha-Zuber[6]模型计算过冷沸腾起始点，采用Jens-Lottes关系式[7]计算过冷沸腾工况下的包壳壁面温度。

Saha-Zuber模型采用努塞尔数Nu和斯坦顿数St作为相似准则判断充分发展泡核沸腾起始点FDB。

其中：

(6)

(7)

(8)

当Pe<70 000时：

(9)

当Pe>70 000时：

(10)

Jens-Lottes关系式为：

ΔTsat=22.65q0.5e-p/8.7

(11)

式中：Pe为贝克莱数；q为热流密度，W/m2；kl为热导率，W·(m·K)-1；ΔTsub为冷却剂过冷度，℃；cp,l为比定压热容，J·(kg·K)-1；G为质量流量，kg·(m2·s)-1；p为堆芯压力；Pa；ΔTsat为壁面过热度，℃。

3) 饱和流动沸腾

采用Chen关系式[8]计算饱和流动沸腾工况下的换热系数。Chen关系式认为饱和沸腾和两相强制对流蒸发区内均存在两种基本传热模式：泡核沸腾传热和强制对流传热，可表示为：

q=hmac(Tw-Tl)+hmic(Tw-Tsat)

(12)

(13)

(14)

式中：hmac、hmic分别为强制对流换热系数和泡核沸腾换热系数，W/(m2·K)；Tw、Tl和Tsat分别为壁面温度、流体温度和流体饱和温度，℃；F为强化因子；kl为热导率，W·(m·K)-1；ρl、ρg分别为液体和气体密度，kg·m-3；hlg为汽化潜热，J·kg-1；Δpsat为壁面过热度ΔTsat所对应的压差，Pa；x为含气率；S为滑速比；σ为表面张力，N·m-1。

4) 临界热流密度模型

采用Bernath关系式[9]计算研究堆低压、低流量工况下的临界热流密度(CHF)：

qCHF=hCHF(Tw-Tl)

(15)

(16)

(17)

式中：qCHF为临界热流密度，W/m2；v为流体速度，m/s；De和Dh分别为水力学直径和流体热当量直径，m。

5) CHF后换热模型

当燃料元件表面热流密度超过CHF时，换热模式转化为过渡沸腾或膜态沸腾工况。

过渡沸腾采用Cheng换热关系式[10]：

exp(0.005G+0.018 8ΔTsub)

(18)

膜态沸腾采用Bromley换热关系式[11]：

(19)

式中：kg为气体热导率，W·(m·K)-1；g为重力加速度，m·s-2；Tg为气体温度，℃；μg为气体黏度，Pa·s。

6) 单相气体换热

采用Sieder-Tate关系式[12]计算单相气体换热：

(20)

1.3 自然循环流量模型

XAPR依靠堆芯自然循环进行冷却，即堆芯冷却剂流量取决于堆芯阻力压头与重力驱动压头之差。通过对动量守恒方程沿轴向进行积分可获得自然循环流量计算公式。

(21)

式中：A为冷却剂通道横截面积，m2；f为摩擦阻力系数；K为形阻系数；l为冷却剂通道长度，m；W为堆芯流量, kg·s-1；ρ为冷却剂密度, kg·m-3；n为控制体数量；下标i表示控制体标识。式(21)左边第1项为流量随时间的变化率，第2项为摩擦阻力压降和局部阻力压降，第3项为重力压降。

1.4 空泡份额模型

反应性引入事故过程中可能发生过冷沸腾和饱和沸腾，需建立过冷沸腾和膜态沸腾工况下的空泡份额模型。本文采用Saha-Zuber模型[6]计算过冷沸腾起始点和过冷沸腾空泡份额，采用漂移流模型计算饱和沸腾下的空泡份额。

1.5 程序开发

基于以上数学物理模型开发了适用于XAPR的瞬态安全特性分析程序TSAC-XAPR。为更加精确计算堆外池水温度，将堆外池水划分为3个控制体，分别为堆池底部控制体、堆池下降段控制体及堆池上部控制体。最终通过数学建模获得一系列用于模拟XAPR动态特性的偏微分方程，继而采用适用于刚性问题求解的吉尔算法[13]进行求解。所开发的TSAC-XAPR程序流程图如图2所示。

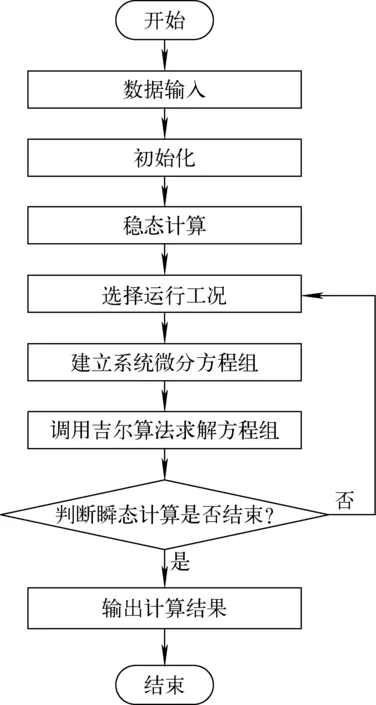
图2 TSAC-XAPR程序流程图Fig.2 Flow chart of TSAC-XAPR code

2 结果讨论

2.1 稳态计算结果

采用TSAC-XAPR程序计算了XAPR的稳态工况，并将稳态计算结果与反应堆稳态运行值及PRTHA程序稳态计算值进行比较，以验证所开发程序的准确性和可靠性。PRTHA是一个子通道程序，由陈立新等[14]基于CPBRA-Ⅳ而开发，结合了XAPR的自身特点，适用于低温、低压研究堆的热工水力分析。此外，稳态计算结果还将作为瞬态计算的初始输入参数。图3示出TSAC-XAPR程序计算得到的稳态关键热工水力参数。表1列出2 MW稳态工况下TSAC-XAPR程序计算值与XAPR稳态运行值的比较，二者相对误差在10%以内。考虑到XAPR每次开堆即使在相同功率下稳态运行，由于实验样品、室温及探测系统误差，最大燃料温度、堆池水温等参数也存在一定的偏差，所以认为TSAC-XAPR程序计算值与运行值的误差是可接受的。表2列出2 MW稳态工况下TSAC-XAPR与PRTHA程序计算值的对比，二者非常接近，相对误差在5%以内，进一步证明本文模型和程序可用于XAPR瞬态安全分析。

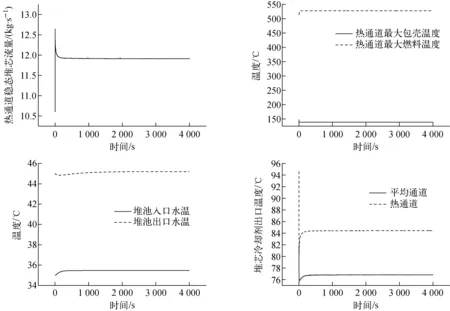
图3 稳态关键热工水力参数随时间的变化Fig.3 Key thermal-hydraulic parameter variation with time under steady state

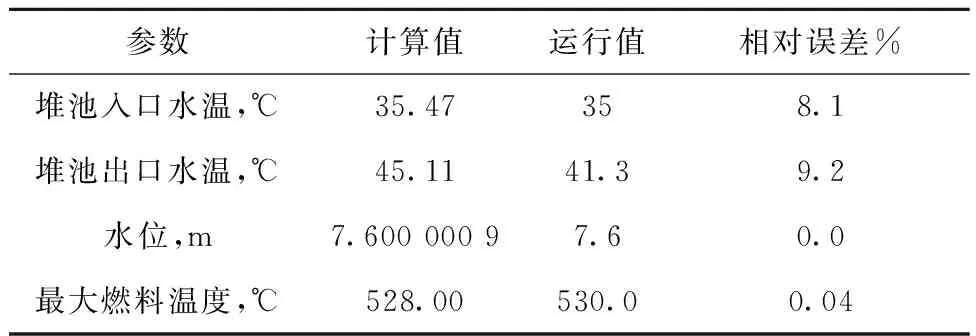
表1 稳态工况下TSAC-XAPR程序计算值与运行值的比较Table 1 Comparison of TSAC-XAPR code calculation value and operating value under steady state

2.2 反应性引入事故

反应堆在高功率运行时堆芯燃料温度较高，最小偏离泡核沸腾点较小，该工况下发生控制棒失控抽出事故会给反应堆内引入较大的正反应性，功率及燃料温度上升较快，容易超出安全限值，从而威胁到反应堆安全，因此本文重点研究高功率运行工况下反应堆控制棒失控抽出后所引入的正反应性对反应堆安全特性的影响。由于XAPR的控制棒速率可以在0～800 mm/min之间调节，控制棒可能以不同的速率失控连续抽出。此外，如果发生控制棒失控弹出事故，将会引入一阶跃反应性。考虑到上述因素，本文进一步分析不同反应性引入方式对反应堆安全特性的影响。

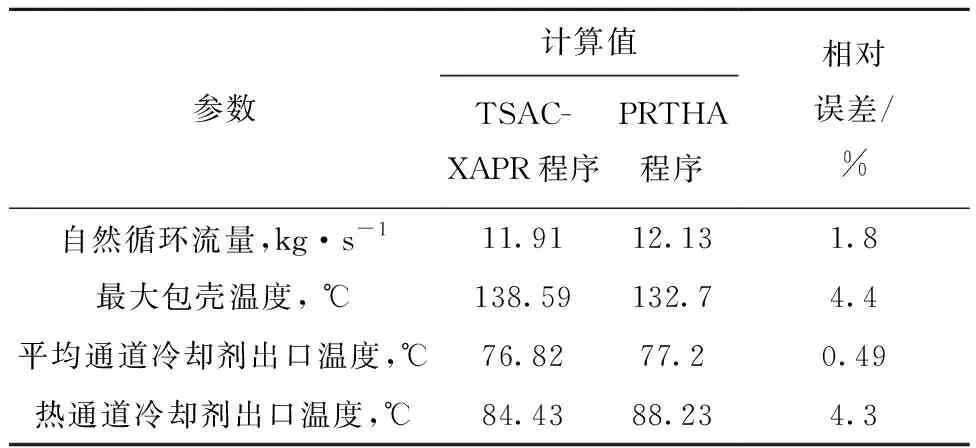
表2 稳态工况下TSAC-XAPR与PRTHA程序计算值的比较Table 2 Comparison of TSAC-XAPR and PRTHA code calculation value under steady state

1) 不同运行功率下的反应性引入事故

本文分别模拟了运行功率为2、2.2、2.65及2.7 MW 4种不同工况下的反应性引入事故瞬态。计算时设置当堆芯在不同功率水平下稳定运行1 000 s后以二阶多项式曲线形式在14.25 s内逐渐引入价值为1 889.2 pcm的正反应性(XAPR稳态运行所允许的提棒引入最大反应性)。图4为2 MW额定功率运行工况下，外部反应性引入曲线及各种反应性反馈曲线随时间的变化。由图4可看出，外部引入的反应性很快被XAPR自身所具有的负反馈机制所抵消，其中起主要作用的是燃料多普勒反馈效应。图5示出不同运行功率水平下堆芯关

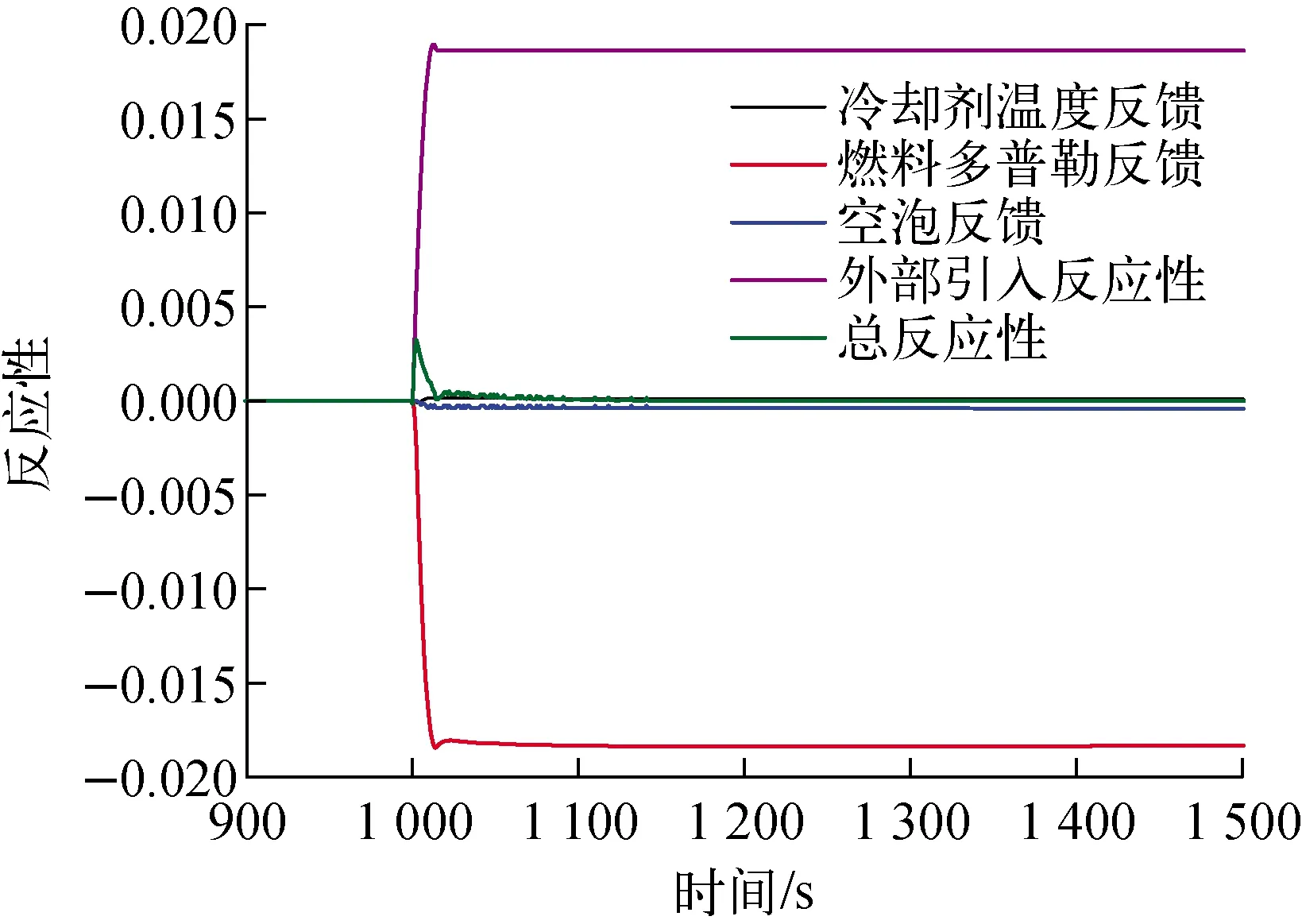
图4 反应性随时间的变化Fig.4 Reactivity variation with time

键热工水力参数对反应性引入事故瞬态的响应，包括堆芯相对功率、流量、出口空泡份额、最大包壳温度、最大燃料温度及最小偏离泡核沸腾点(MDNBR)，其中功率为瞬态功率与初始稳态额定功率的比值，即相对功率P/P0。从图5a可看出，当堆芯处于额定功率水平(2 MW和2.2 MW)，堆内引入较大的反应性时，反应堆功率先急剧上升随后有所下降，最终达到新的稳定功率。这是因为引入的正反应性使反应堆功率迅速上升，且堆芯燃料温度也随之上升，而XAPR堆芯装载的UHZr1.65燃料具有较大的瞬发负温度系数，因而功率的上升引发瞬发负温度效应，产生负反应性反馈，从而使反应堆功率有所降低，最终稳定在相对更低的水平。而当堆芯功率增加到2.65 MW和2.7 MW时，较大的功率使得堆芯冷却剂温度升高，并出现饱和沸腾，引起冷却剂出口空泡份额振荡。此时由于功率2.65 MW对应的出口空泡份额较小，所以两相沸腾换热有利于自然循环流量的增加，且流量振荡较小，所以并未引起最大燃料温度、最大包壳温度及MDNBR的振荡。但当功率达到2.7 MW时，堆芯冷却剂出口空泡份额进一步增加，堆芯出现膜态沸腾，导致自然循环流量下降，并剧烈振荡，流量的振荡进一步引起堆芯功率、最大包壳温度、最大燃料温度及MDNBR振荡，且由于堆芯功率过高而堆芯流量降低，导致MDNBR低于安全限值1.3。

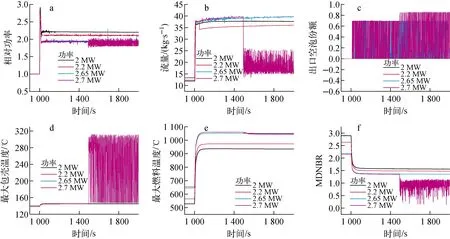
图5 不同运行功率水平下堆芯关键热工水力参数对反应性引入事故瞬态的响应Fig.5 Core key thermal-hydraulic parameter transient variation under reactivity insertion accident with different operating powers

2) 不同反应性引入方式下的事故

图6a为本文所模拟的5种不同方式的反应性引入，分别对应二阶多项式曲线反应性引入、阶跃反应性引入及3种不同速率反应性引入。计算时同样设置当堆芯在2 MW额定功率下稳定运行1 000 s后以不同方式引入反应性，而最终引入的反应性均为1 889.2 pcm(提棒引入的最大反应性)。图6b为不同反应性引入方式下的反应堆总反应性变化。由图6b可看出，虽最终引入的反应性相同，但由于引入方式不同导致反应性在达到稳定之前的变化过程不同，其中阶跃引入方式由于引入反应性速率过快，达到瞬发超临界，从而引起反应性急剧升高，但由于XAPR的UHZr1.65燃料具有较大的瞬发负温度系数，能立即产生较大的负

反馈效应，所以使反应性引入过程呈现幅值较大的变化。而速率最慢的线性反应性引入方式(117 s)对应的反应性变化最为平缓，但最终不同反应性引入方式下的反应性均趋于稳定值0。

图7为不同反应性引入方式下堆芯关键热工水力参数对反应性引入事故瞬态的响应。由图7可见，在反应性引入过程中，由于阶跃引入方式下堆芯反应性变化最为剧烈，从而导致堆芯相对功率、流量及最大燃料温度等参数随之剧烈变化，尤其相对功率变化的峰值最大，而反应性引入速率最小的线性反应性引入方式引起的参数变化最为平缓，但由于最终引入的反应性一致，同时XAPR具有较大的燃料负反馈效应，所以即使在不同方式反应性引入工况下，最终堆芯热工参数均趋于一致，且均在安全限值内，证明XAPR具有良好的固有安全特性，且对不同方式反应性引入事故有较好的缓解适应机制。但考虑到XAPR的安全裕度和稳定性，在启堆或提升功率的过程中应尽量避免快速阶跃引入反应性，防止瞬发超临界现象的发生，应当选择合理的控制棒棒速，以避免过快的反应性引入导致功率迅速上升，堆芯冷却剂出现沸腾，从而引起堆芯流量、最大燃料温度及MDNBR等参数的振荡。

3 结论

本文采用自主开发的瞬态安全分析程序TSAC-XAPR计算了XAPR在反应性引入事故下的关键热工水力参数的动态响应，并分析了反应堆在不同功率运行水平和不同反应性引入方式下的安全特性。程序的稳态计算结果与参考值吻合较好，证明了所开发程序的准确性和可靠性。反应性引入事故瞬态计算结果表明：在额定功率水平下发生反应性引入事故时，反应堆能依靠自身固有负反馈机制促使堆芯恢复稳态并处于安全限值以内。而当堆芯运行功率水平提高到2.7 MW时，由于功率过高，堆芯内出现两相饱和沸腾，引起空泡份额和堆芯流量等关键热工水力参数的振荡，导致堆芯MDNBR低于安全限值，从而威胁到反应堆安全。此外，不同反应性引入方式的模拟计算结果显示：阶跃引入反应性会使堆芯参数的变化最为剧烈，而线性引入反应性的速率越慢，堆芯的参数动态响应越平缓，所以在启堆或提升功率时应尽量选择合理的控制棒提升速率，避免快速阶跃引入反应性导致瞬发超临界现象的发生。

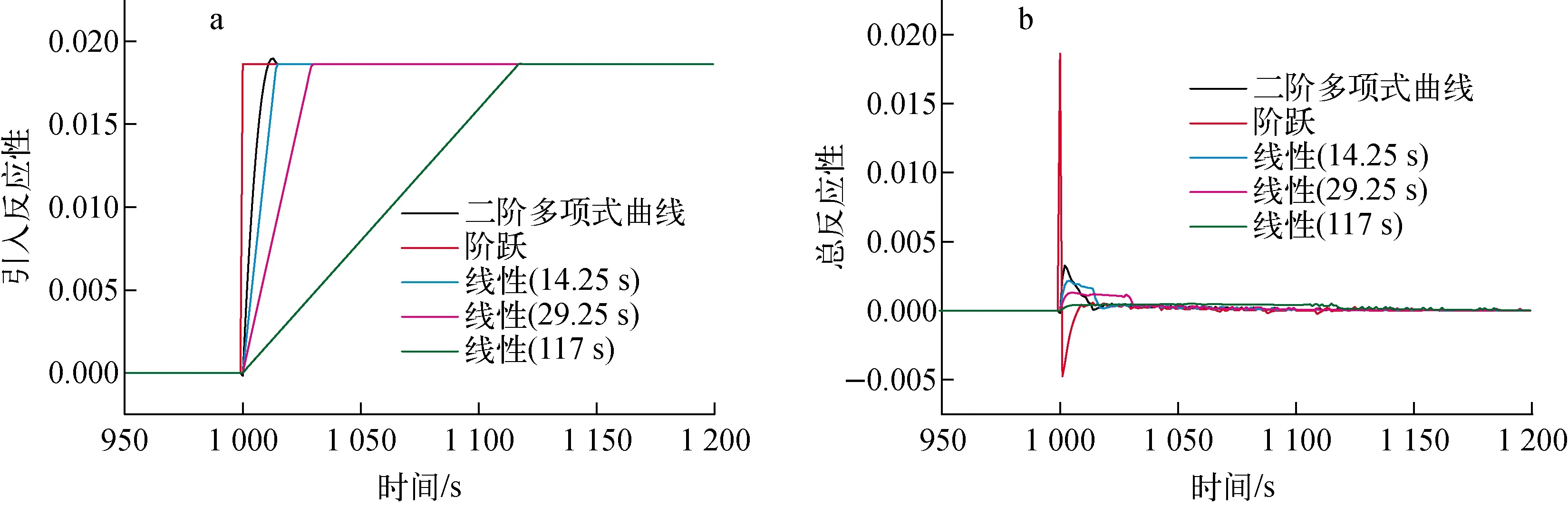
图6 引入反应性(a)和总反应性(b)随时间的变化Fig.6 Reactivity insertion (a) and total reactivity (b) variations with time

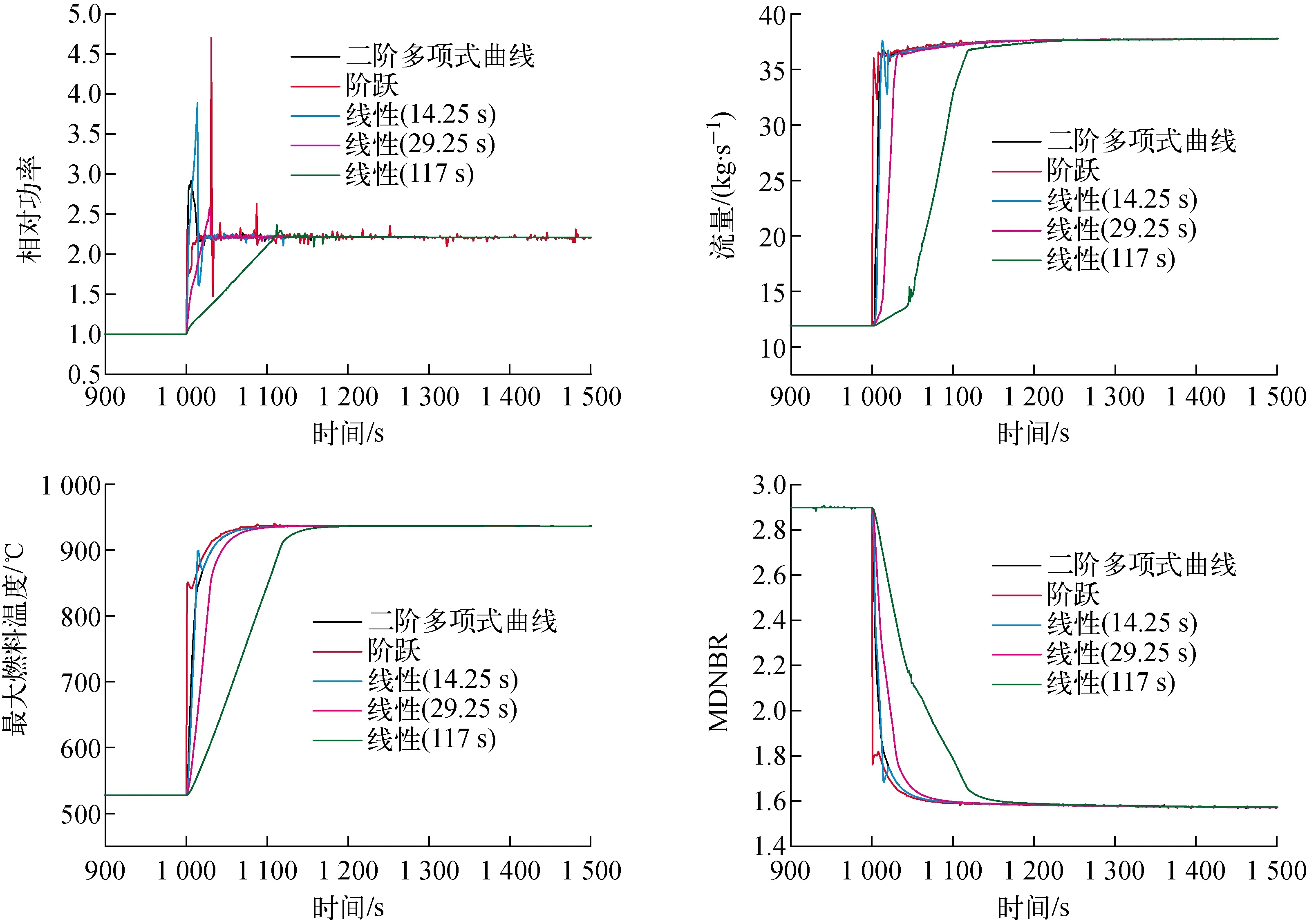
图7 不同反应性引入方式下堆芯关键热工水力参数对反应性引入事故瞬态的响应Fig.7 Core key thermal-hydraulic parameter transient variation under reactivity insertion accident by different insertion modes