动态规划方法在斜拉桥模型索力优化中的应用

方有亮， 武 铮， 张 颖

(河北大学建筑工程学院, 保定 071000)

斜拉桥在众多桥梁中具有杰出的结构特点和技术优势，是全世界建造最多的桥梁结构之一。但是在实际桥梁建设过程中，由于施工过程复杂，工程周期长，建设期间会有很多外部因素对斜拉桥的成桥状态造成影响，最后的成桥状态会与理想状态有所偏差，所以需要优化斜拉桥的施工过程。郭伟[1]采用正装迭代法计算斜拉桥的施工索力，按照施工顺序，采用正装迭代法优化施工索力，以达到成桥的目标状态，表明成桥索力能得到很好的收敛，满足工程计算的精度要求；王伟坤等[2]研究了中国首座斜拉独塔单索面钢-混凝土组合斜拉桥，运用频率法测索原理，实测拉索自振频率得到实际索力，表明运用这种方法可在现场快速确定出下一根索一次张拉到该桥期望值的增量；Changfu等[3]针对一种新型斜拉桥的结构特点，提出了实用的拉索拉力和拱轴优化方法,在进行参数分析下，成桥索力收敛，计算精度提高。

动态规划方法是把一个多阶段的问题转化为多个单阶段的问题，从而求解整个阶段的最优决策问题就转化成求解一系列单个阶段中的最优问题[4]；王鑫淼[5]设计了多搬运机器人两阶段动态路径规划算法，通过调节优先级的方式进行在线协调，结果表明有效地节省了搬运机器人的冲突等待时间；张建[6]建立车位动态规划双目标模型，这种方法能准确得到最优车位分配结果，并且收敛速度极快，响应时间短；谷润平等[7]研究了机场场面滑行路径动态规划问题，结果表明使航班总体滑行时间有效减少，提高场面运行效率。

现运用动态规划方法[8-9]进行斜拉桥索力优化，动态规划方法是把整个施工阶段拆分成一系列的单个问题，求解索力张拉过程的最优解，最后完成整个施工，动态规划方法对索力优化过程提出一个新的优化思路和方法。运用Midas软件建模，求出拼接主梁对节点竖向位移和张拉斜拉索对主梁竖向位移的影响矩阵[10]，将影响矩阵同各阶段的理想竖向位移代入动态规划表达式中，运用MATLAB[11-12]程序进行计算，与实验模型形成对比，动态规划方法可以在各个施工阶段都可以与理论值进行比较，可以实时监控整个施工过程，随时校准各个阶段，更好地保证整个施工过程索力的调整。

1 动态规划在斜拉桥索力优化中的应用

斜拉桥在施工过程中，主梁竖向位移只与主梁的装接及斜拉索的张拉有关，忽略其他因素对其影响。则斜拉桥主梁位移和斜拉索的初张拉力满足式(1)的数学关系，该数学关系式同样也是动态规划中的状态转移方程。

Xn+1=Xn+Gnfn+Kn

(1)

式(1)中：Xn+1为第n个施工段结束后主梁的竖向位移；Xn为第n-1个施工段结束后主梁的竖向位移；Gn为在第n个施工段中给第n根索施加单位张拉力对主梁竖向位移的影响矩阵；fn为第n根斜拉索的初张拉力；Kn为第n个施工段拼接第n根主梁对主梁竖向位移的影响矩阵。

影响矩阵Kn、Gn是已知的，力fn是未知的，为了求解每一施工段的初张拉力，可建立目标函数E为

(2)

式(2)中：A(n×n)和B(n×n)是加权矩阵；Un为各施工段结束后主梁的理想竖向位移。不同的斜拉桥A矩阵和B矩阵都不相同，在进行求解时可做调整。设gN(X)为第n阶段E的最小值，也就是指标函数：

(3)

将式(2)代入式(3)，可得：

A(Xn+1-Un)+(fn,Bfn)]

(4)

将式(1)代入式(4)中，可得:

A(Xn+Gnfn+Kn-

Un)+(fn,Bfn)]

(5)

将式(5)进行配方，可得：

Hn(fn+MnXn+Nn)+

rn(Xn)]

(6)

式(6)中：

(7)

(8)

(9)

(10)

由式(6)可知若gN(X)最小时，有：

fn=-MnXn-Nn

(11)

将有关Mn、Nn的函数代入式(11)，可得：

(12)

式(12)中：

Ln=(Un-Kn)

(13)

由于Un是每阶段主梁的理想竖向位移，故其可以通过计算求出来，最终可得：

(14)

式(14)中：H1、G1和L1都是已知的，X1是第一施工段拼接第一根主梁未张拉斜拉索时主梁的竖向位移，可用Midas/Civil软件进行求解，故f1可以被求出来。

2 模型试验

2.1 斜拉桥模型

斜拉桥两边完全对称，左右两侧的索力、梁和塔的内力及位移也完全对称，也就是说分析斜拉桥模型一侧的数据就可以推出来另一侧的数据，为了节省实验材料和测量仪器，同时对实验结果不造成任何影响，本实验最终只研究了图1所示的半侧结构。为接近于真实工况，采用加载方式模拟配重。每个节点上放置一质量为5.1 kg的重物。斜拉桥的主梁和塔的材料都为钢材，截面长度为50 mm，宽度为30 mm；斜拉索的材料为钢丝绳，直径为2 mm，高跨比为30/4 200=1/140，符合斜拉桥的取值范围,具体的材料参数如表1所示。

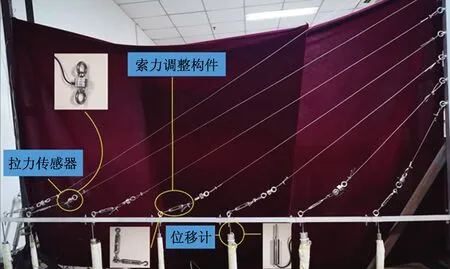
图1 实验系统Fig.1 Experimental system

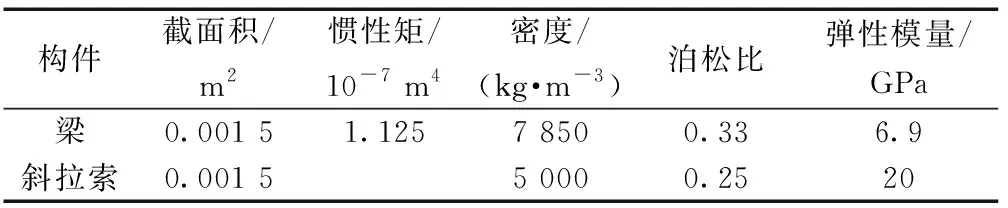
表1 材料参数Table 1 Material parameters

两片钢板及螺栓做固定处理，需要注意的是固定时两钢板必须加紧，以减小误差。同时，节点上放置重物以达到放大刚度矩阵的目的。斜拉索与力传感器、主梁的固定主要通过索扣来实现，斜拉索的加载主要通过张拉千斤顶来实现。斜拉索与力传感器、主梁的固定通过索扣来实现，图2所示为斜拉索的具体连接方式。

图2 斜拉索固定与连接Fig.2 Cable fixation and connection

2.2 实验过程

实验过程共计7个阶段，按动态规划方法，先用Midas/Civil计算出合理成桥时斜拉桥主梁的竖向位移，然后求出主梁施工和张拉斜拉索对主梁竖向位移的影响矩阵，将这些影响矩阵同各阶段的理想竖向位移写入动态规划程序中，计算出斜拉桥的初张拉力，分步张拉斜拉索，用位移计读取各个施工过程节点的位移。部分实验过程如图3所示。

图3 部分实验过程Fig.3 Partial experimental process

3 有限元模拟

3.1 模型建立

运用零位移法[13]来确定成桥状态时的索力，在斜拉桥模型建立过程中，约束斜拉索与主梁连接点的位移，得出各个阶段的理论值，与优化结果形成对比。采用Midas/Civil建立斜拉桥模型，边界条件均采用固定边界，斜拉桥各个施工阶段的模型如图4所示。

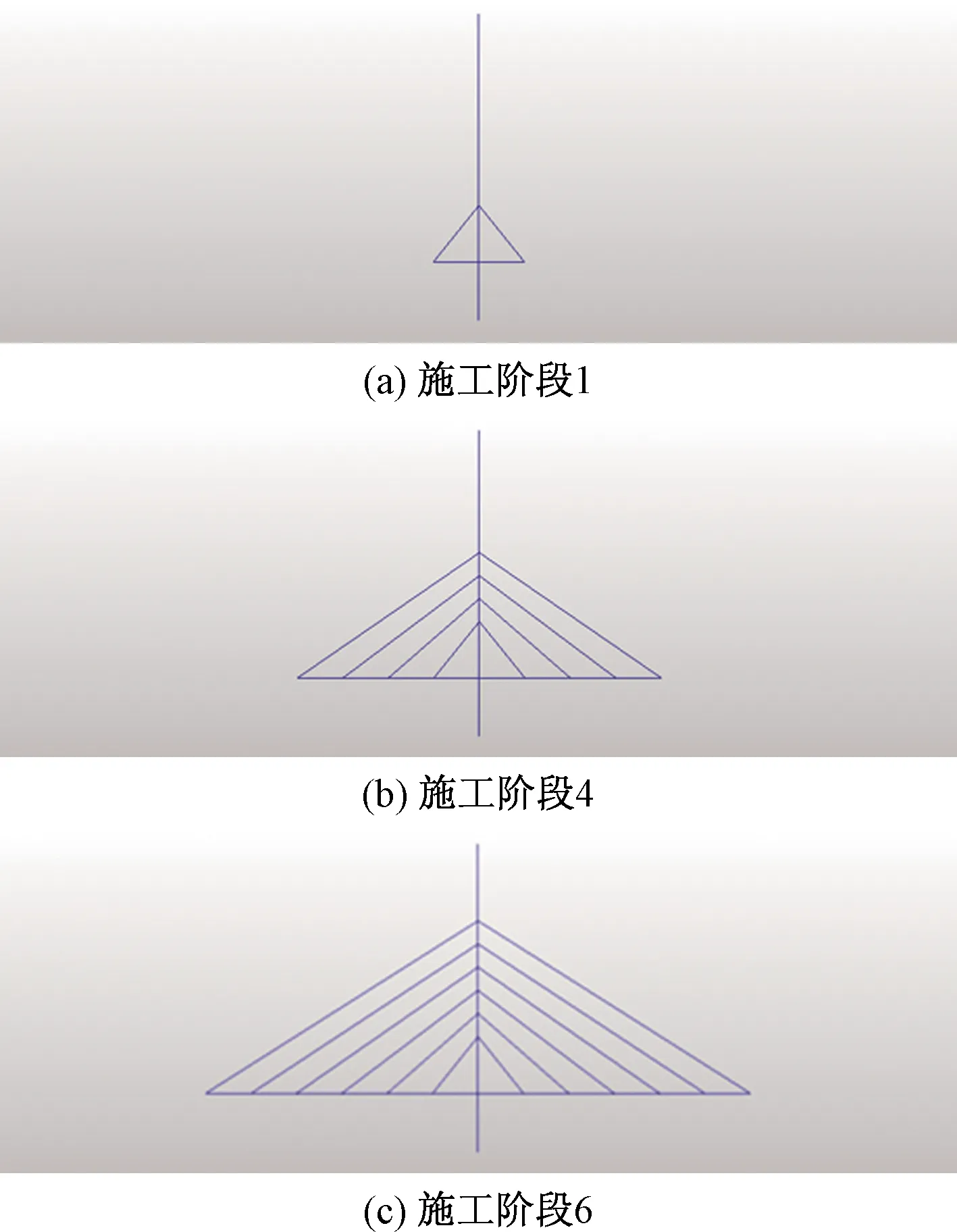
图4 各阶段斜拉桥模型Fig.4 Models of cable-stayed bridges in different stages

假定该斜拉桥模型采用悬臂法的方法进行施工，模拟斜拉桥施工阶段过程，从而得出各个施工阶段的理想位移，采集每个阶段的理想位移，最终将理论计算结果与动态规划结果进行对比。具体施工段划分如表2所示。

表2 斜拉桥模型各施工阶段的工作Table 2 Work of cable-stayed bridge model at different construction stages

3.2 动态规划优化结果

采用Midas/Civil中提供的未知荷载系数法。约束范围在-1～1 mm[14]。此荷载系数即为拉索的初拉力。运用Midas/Civil有限元软件，求解出影响矩阵[15-16]Kn和Gn求解出来(表3、表4)，将影响矩阵代入式(1)。

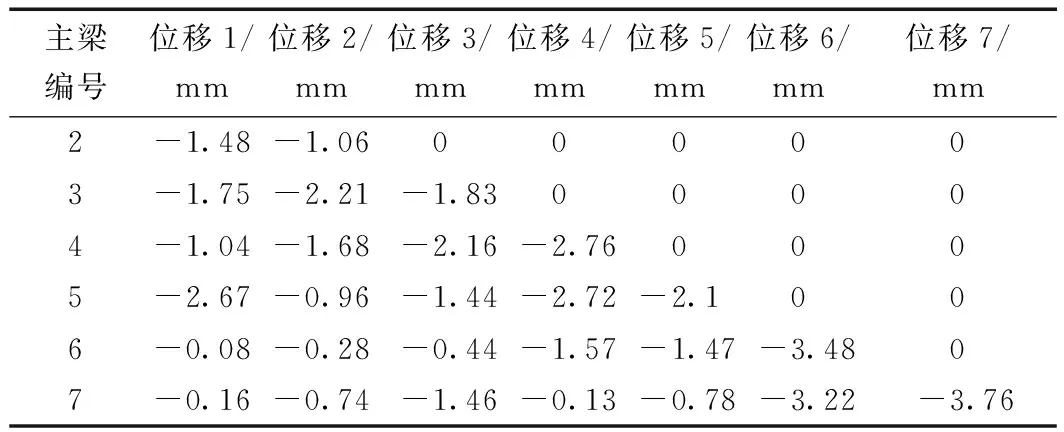
表3 拼接主梁的影响矩阵Table 3 The influence matrix of spliced girders

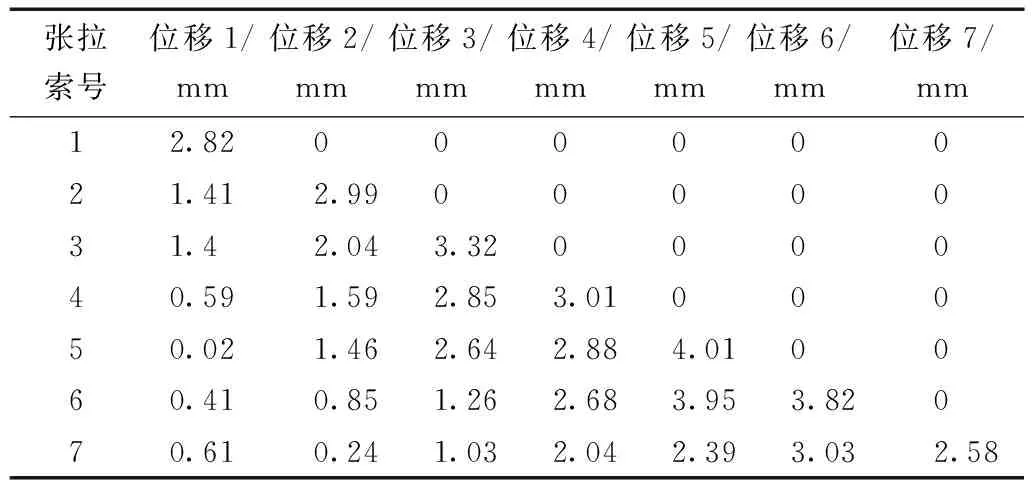
表4 张拉斜拉索的影响矩阵Table 4 Impact matrix of stayed cables

将求解出的影响矩阵代入动态规划进行优化，求解出各个施工阶段的初始张力拉力以及各个施工阶段施工完成后各主梁节点的竖向位移。

3.3 结果对比

由图5可知，动态规划求出索力与理论计算求出的索力增长趋势和幅度相似，1～7号索，索力逐渐变大，符合实际桥梁的斜拉索索力变化趋势，2号斜拉索索力出现突变，应该是在第1段主梁拼接时桥塔与主梁的连接不牢固，导致第2段主梁拼接并加载荷载后索力出现一个突变。索优化后，索力减小，而且相比优化之前索力，优化后，索力变化更加均匀，斜拉索的索力的变化幅度也更平滑。

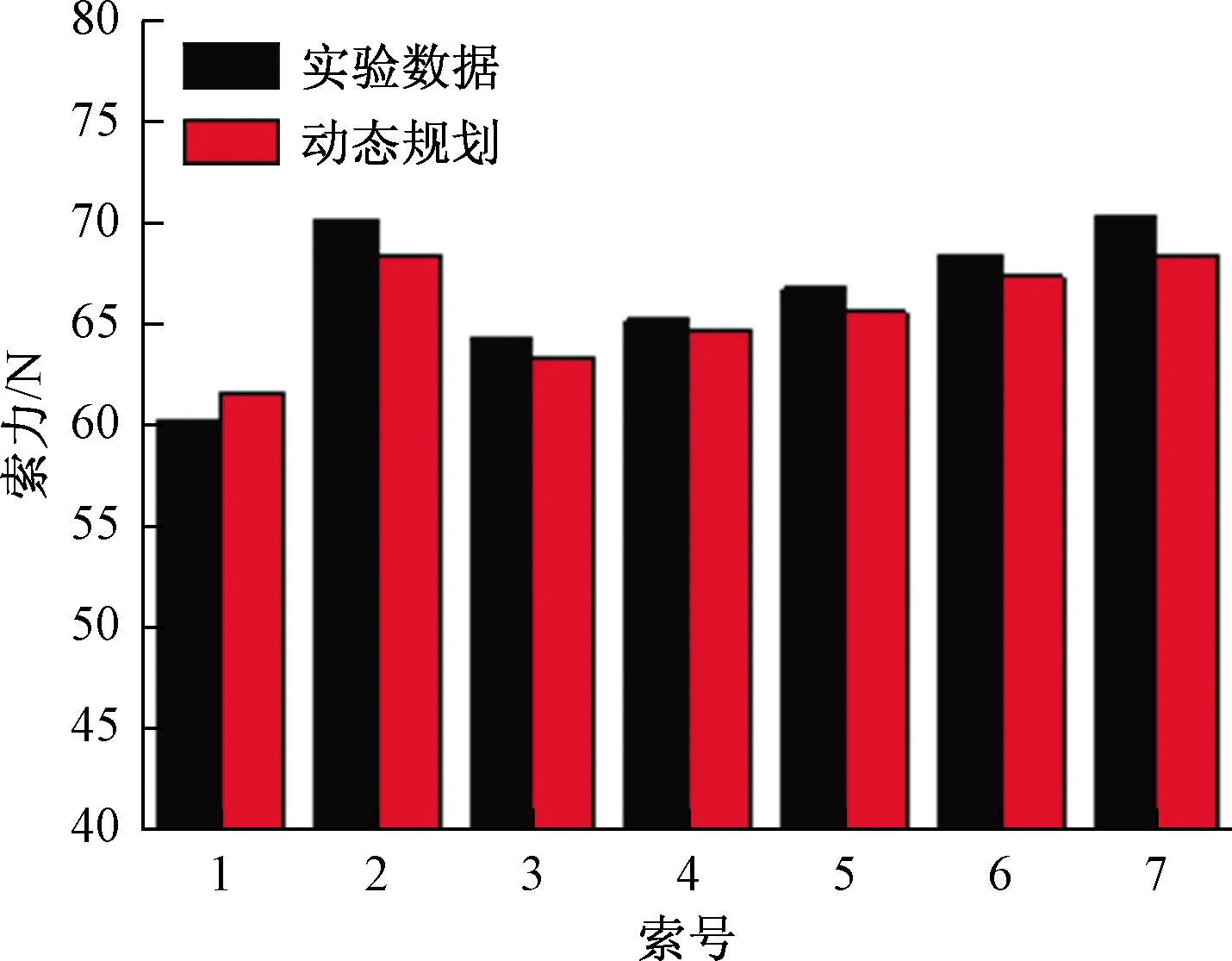
图5 索力对比Fig.5 Comparisons of cable forces

由图6可知，从第2施工阶段到第7施工阶段，节点位移逐渐趋于平滑，随着斜拉桥施工的进行，主梁的各个节点位移趋于0，说明随着施工阶段的进行，斜拉桥受力均匀，而且达到了设计之初的要求，从第2施工阶段到第7施工阶段，位移变化在0.6 mm以内，最终主梁的各个节点位移在±0.05以内，主梁趋于水平。动态规划结果与实际实验得出的节点位移趋势相同，节点的误差在0.1 mm以内，在误差范围内。动态规划方法可以在各个施工阶段与理论值进行比较，可以实时监控整个施工过程，随时可以校准各个阶段，检查是否施工过程中与理论值有大的偏差，并且随着斜拉桥施工的进行，动态规划计算出的节点位移相比理论计算值在减小，相比优化前各节点位移在减小，随着施工阶段的增加，每个施工阶段的整体误差也减少，斜拉桥的斜拉索越多，跨度越大，动态规划方法的优化性更好，对于大跨斜拉索的施工会有更好的指导意义。

图6 各施工阶段节点位移对比Fig.6 Comparison of node displacement in each construction stage

由图7可以看出，相比于优化前，优化后的斜拉桥主梁的弯矩减小，分布合理。主梁的力学性能得到了改善，由图8可以看出，索塔的弯矩也变得更加合理。

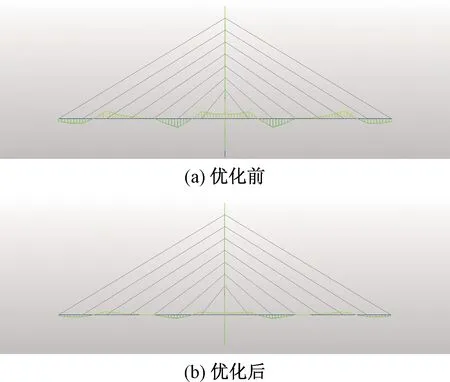
图7 优化前后主梁弯矩对比Fig.7 Bending moment comparison of main girder before and after optimization

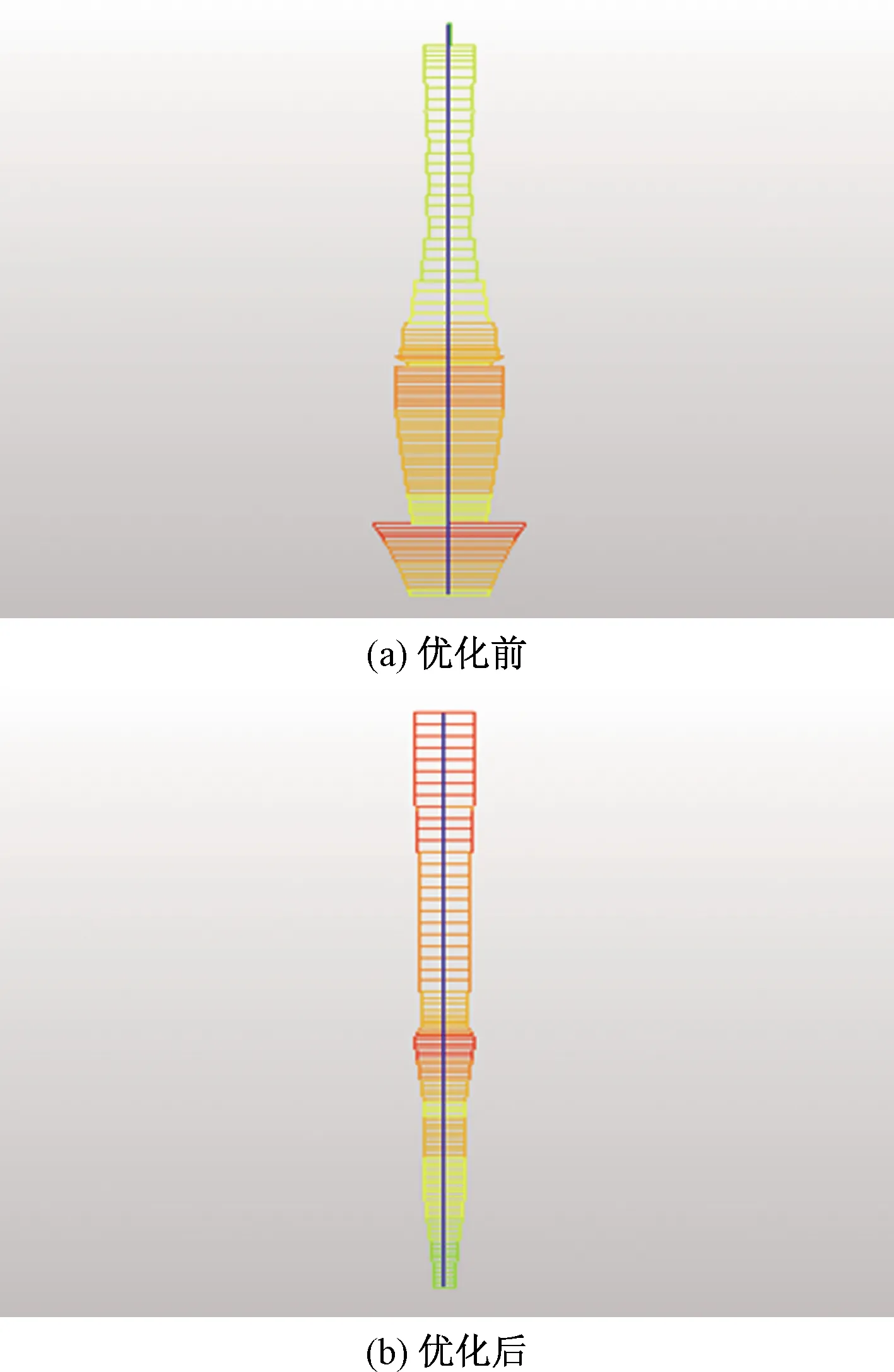
图8 优化前后索塔横梁弯矩对比Fig.8 Bending moment comparison of pylon beam before and after optimization

4 结论

运用动态规划方法对一座独塔斜拉桥进行了施工过程索力优化。用零位移法确定每一个施工阶段的各个节点的理想位移和索力，计算出合理成桥时斜拉桥主梁的竖向位移，并以此为参考求出主梁施工和张拉斜拉索对主梁竖向位移的影响矩阵，将这些影响矩阵同各阶段的理想竖向位移代入动态规划程序中，求解斜拉桥各个施工阶段的初始张拉力，得到各个阶段施工完成后每个主梁节点的竖向位移。

相比理论值，用动态规划方法优化后的索力最后成桥状态受力均匀，内力得到了更合理的分布，弯矩分配更加合理。运用动态规划方法，可以计算出各个施工阶段的位移，模拟了整个施工过程，在斜拉桥施工过程中，随时进行比较，斜拉桥主梁的竖向位移与各阶段理想竖向位移理论相比，发现二者相差很小，并且随着施工阶段的增加，整体误差也随之减少，对于大跨斜拉索的施工会有更好的指导意义。

由实验室模型进行实验可知，动态规划结果与实际实验结果具有一致性，用动态规划方法进行斜拉桥施工索力优化是完全可行的，这种新的方法有很大的理论价值，对实际工程具有一定的指导意义。