考虑燃料消耗的飞机副油箱燃油晃动等效建模

苗 楠， 刘战合， 王晓璐， 王 菁， 田秋丽

(1.郑州航空工业管理学院航空工程学院， 郑州 450046； 2.郑州航空工业管理学院经济学院， 郑州 450046)

为提高飞机的续航性能，通常在机身或机翼下面加挂副油箱[1]。在非满油状态下，飞机副油箱内的燃油将随飞机的机动飞行而发生晃动。燃料的晃动将施加在飞机上一定作用力和力矩，同时影响飞机的质心位置，从而影响其飞行品质和飞行安全[2]。同时，随着燃料的消耗，副油箱内燃油的晃动动力学特性也将发生改变。因此，燃油晃动动力学行为的描述是航空工程中颇为关心的问题。

对液体晃动行为的分析通常从理论研究、数值模拟和实验研究三方面展开[3-4]。相比于理论和实验研究，数值方法在对不同形状容器的适用性及研究成本等方面有其独特优势。计算流体动力学(computational fluid dynamics, CFD)方法通过直接求解Navier-Stokes方程或其简化方程，在时域内对液体晃动进行数值模拟[5]。用于建模验证的CFD软件Flow-3D基于流体体积法(volume of fluid, VOF)编写，在自由液面追踪和流动仿真方面较为成熟，在液体晃动仿真中得到了广泛应用[6-7]。

此外，考虑到计算效率等方面的要求，航天工程中常用等效力学模型描述飞行器内液体的晃动动力学行为[8]。常用的等效力学模型有单摆模型和弹簧-质量模型两种形式，如图1[9]所示，二者在液体发生小幅晃动时等价，且等效力学模型参数之间存在简单的转换关系。

图1 等效力学模型[9]Fig.1 Equivalent mechanical model[9]

然而，由于飞机油箱外部形状及内部结构的复杂性，航空工程中的燃油晃动问题目前较多地采用数值方法进行研究[10-11]。在燃油晃动的等效力学模型建立方面，主要困难在于结构复杂导致等效模型参数难以获取。为提高等效建模方法对于不同油箱形状和结构的适用性，基于势流理论和有限元法[5]进行液体晃动等效建模，以飞机副油箱为例建立了固定充液高度及考虑燃油消耗两种情况下的单摆等效力学模型，并将其计算结果与CFD软件Flow-3D的仿真结果进行对比验证。

1 油箱及液体模型

飞机副油箱多采用流线型设计，将副油箱近似为中间圆柱段、两端半椭球的轴对称形状，如图2所示。圆柱段半径和长度分别取为r=0.25 m、lc=2.4 m。两端半椭球大小相同，均为绕长轴(x轴)旋转而成的旋转椭球体的一半，长半轴和短半轴分别取为a=1 m、b=r=0.25 m。

图2 油箱形状及坐标系定义Fig.2 Tank shape and coordinate system definition

建立油箱本体坐标系Obxyz，其中坐标原点Ob点位于副油箱的几何中心，x轴即纵轴为油箱对称轴并以指向机头方向为正，y轴即立轴以向上为正，z轴根据右手法则确定，以指向右翼为正。假设初始时刻，副油箱内的燃油在沿y轴负向的重力作用下聚集在油箱底部，则充液高度范围可表示为(-0.25, 0.25) m。为进行燃油晃动等效建模、且考虑到实际工程中的油箱使用情况，针对充液高度(相对于油箱中心Ob点)ys=-0.22：0.02：0.22 m的不同情形，在有限元软件MSC.Patran中建立液体初始状态的几何模型，并进行网格划分。建模及网格划分结果以ys=±0.06 m和ys=±0.2 m共4种充液情形为例给出，如图3所示。

图3 液体初始形态及网格划分Fig.3 Liquid initial configuration and mesh generation

同时，为对所提出的等效建模方法的有效性和准确性进行验证，在CFD软件Flow-3D中同样建立油箱模型。在代表流体流动区域的空腔外部建立长方体实体以包裹油箱，并以立方体单元对含油箱的长方体区域进行网格划分。立方体单元各边尺寸均设定为0.02 m，网格数量为240×28×28个。假设副油箱吊挂于右侧机翼下，在飞机飞行过程中随飞机发生平动且绕飞机重心转动，因此将CFD仿真的坐标原点平移至飞机重心，此时副油箱中心Ob点的坐标表示为(-0.2,-0.5, 2) m。沿重力方向即-y轴方向设置充液条件，充液高度ys=0 m和ys=±0.06 m的结果如图4所示。液体选为航空煤油RP-3[12]，密度为791.5 kg/m3，动力黏度为1.289×10-3(N·s)/m2。

图4 不同充液情况下CFD油箱及液体模型Fig.4 CFD tank and liquid model under different fill situation

2 固定充液高度下的晃动等效建模

首先对固定充液高度或固定充液比下的副油箱内燃油晃动进行等效建模。根据等效原则，等效系统与原系统的总质量、质心位置、转动惯量对应相等，对油箱的作用力、作用力矩和运动动能等也应分别对应相等。由此，可根据文献[5]中给出的方法，基于势流理论和有限元网格划分结果计算出晃动质量的相关参数，如x轴方向第一阶晃动模态所对应的晃动质量即单摆摆球质量mx，x轴方向单摆摆长lx及悬挂点相对于Ob点的高度hx，x轴晃动质量关于Ob点的惯量张量Ix及晃动模态阻尼比ζx等。类似地，可计算得到z轴方向第一阶晃动模态所对应的晃动质量mz，单摆摆长lz及悬挂点高度hz，关于Ob点的惯量张量Iz及阻尼比ζz等。

根据等效关系，有：

mliq=mx+mz+m0

(1)

mliqhc=mxhx+mzhz+m0h0

(2)

Jliq=Ix+Iz+I0+I′0

(3)

式中：mliq为液体总质量；m0为静止质量；hc和h0分别为液体总质心和静止质量块质心相对于Ob点的高度；Jliq代表液体等效刚体关于Ob点的惯量；I0和I′0分别为静止质量块相对于其质心的惯量张量和其质心关于Ob点的惯量。根据副油箱的对称性可知，x轴和z轴晃动质量的平衡位置及静止质量块的质心均位于Oby轴上。由上述等效关系，即可求得晃动质量和静止质量块的所有参数，并计算等效系统对油箱的作用、力矩和质心位置等。

针对不同充液高度，可由该方法计算得到三维副油箱内的液体晃动的单摆等效力学模型参数。由于同样激励作用下，充液比在40%～60%时会施加给油箱更大的作用力和力矩，因此以充液高度ys=0 m和ys=±0.06 m为例，给出单摆等效力学模型的主要参数(表1)，并以俯仰激励为例对等效模型进行验证(参见4.1节)。

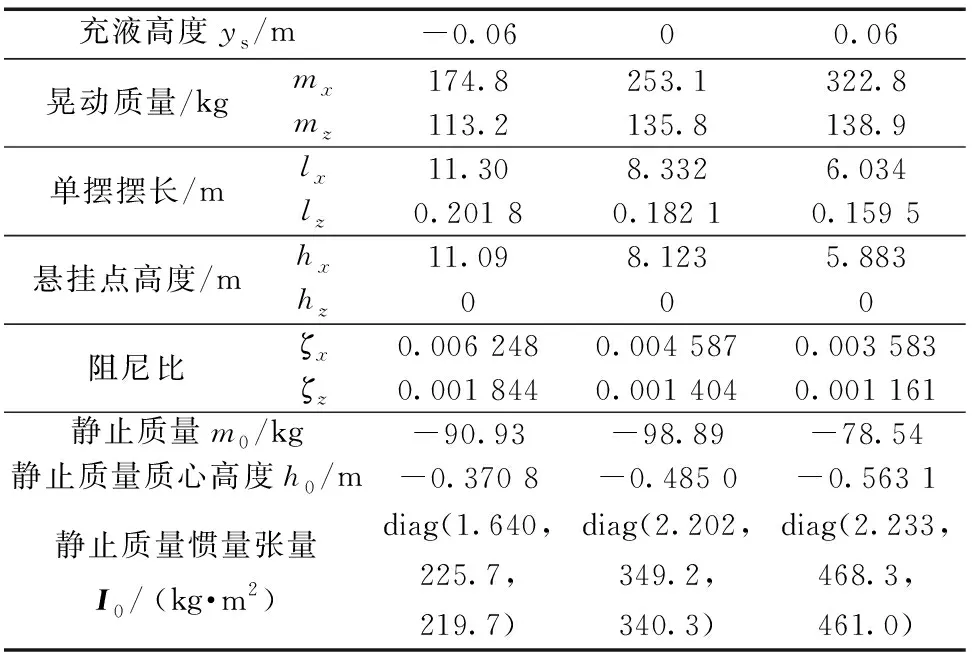
表1 等效力学模型主要参数Table 1 Main parameters of equivalent mechanical model

3 考虑燃料消耗的晃动等效建模

由计算结果可知，随着副油箱内燃油的消耗，不同充液高度将对应不同的等效力学模型参数。若考虑燃油从满箱到接近空箱的全过程，则必须考虑燃油消耗过程中等效模型参数的变化。为研究等效模型参数的变化过程，首先计算不同充液高度上x轴和z轴的晃动质量和摆长，然后由等效条件进一步计算得到静止质量等参数，主要参数随充液高度的变化情况及其线性插值结果如图5所示。

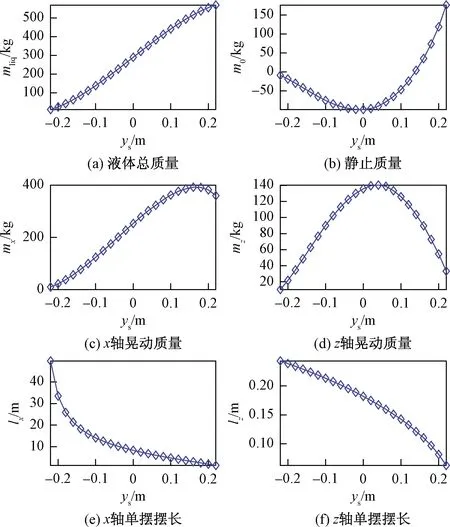
图5 主要等效模型参数线性插值结果Fig.5 Linear interpolation results of main equivalent model parameters

由图5可见，随充液高度的不同，各个等效模型参数变化范围均较大，但变化较为平缓，故可尝试基于线性插值结果近似描述充液比连续变化时导致的等效模型参数变化[13]。具体来说，可根据燃油剩余质量实时计算得到副油箱充液比和充液高度，并以充液高度ys为基准进行线性插值，求得此时单摆等效力学模型中晃动质量和静止质量的所有参数，并计算对油箱的作用力、作用力矩及液体总质心位置。通过与CFD软件的对应计算结果进行对比分析，验证考虑燃料消耗的变充液比燃油晃动等效建模方法的可行性和准确性(参见4.2节)。

4 算例验证

分别以俯仰激励和滚转激励为例，对固定充液比和考虑燃料消耗(变充液比)情形下飞机副油箱内的燃油晃动等效力学模型进行算例分析。给出燃油对油箱的作用力(晃动力)、作用力矩(晃动力矩)、液体质心位置等的等效模型预测结果，并将其与CFD软件Flow-3D的仿真结果进行对比验证。

4.1 固定充液比算例验证

首先对第2节中建立的固定充液比单摆等效力学模型进行验证。假设飞机绕其重心做俯仰简谐运动，俯仰角幅值为15°，周期为10 s，因此俯仰角运动规律可表示为θ=15°sin(0.2πt)。

以充液比50%即充液高度ys=0 m为例，利用CFD软件进行100 s的仿真，期间部分时刻副油箱xy对称面上的液体形态及压强分布如图6所示。

图6 俯仰激励下部分时刻液体形态及压强分布 (ys=0 m)Fig.6 Liquid configuration and pressure distribution at some moments under pitch excitation (ys=0 m)

为验证所建立单摆等效力学模型的有效性和准确性，给出晃动力、晃动力矩和液体质心位置的预测结果，与CFD软件仿真结果的对比情况分别如图7～图9所示。

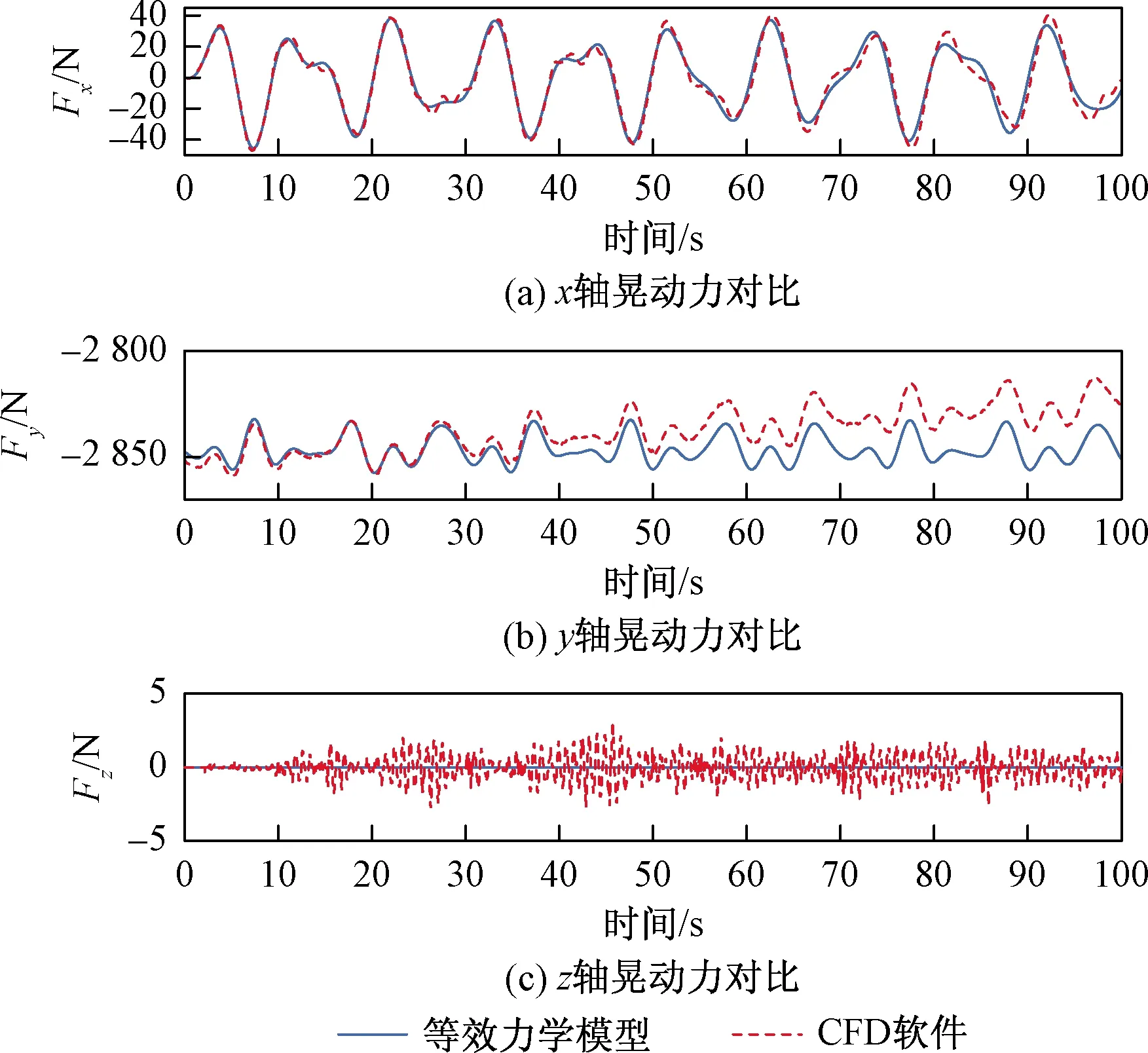
图7 俯仰激励下晃动力对比 (ys=0 m)Fig.7 Slosh forces comparison under pitch excitation (ys=0 m)

图8 俯仰激励下晃动力矩对比 (ys=0 m)Fig.8 Slosh moments comparison under pitch excitation (ys=0 m)

图9 俯仰激励下液体质心位置对比 (ys=0 m)Fig.9 Liquid center of mass comparison under pitch excitation (ys=0 m)

从图7给出的晃动力对比结果可见，俯仰运动将引起x轴方向单摆的晃动，并产生x轴方向晃动力，等效力学模型的预测结果与CFD软件的仿真结果有较好吻合。在y轴方向上也会产生一定程度上作用力的波动，初始阶段等效力学模型与CFD软件吻合较好，但由于CFD仿真的误差累积，其后半段仿真结果与基准值相比有了一定程度上的偏离。由于俯仰激励理论上不会引起z轴方向单摆的运动，因此z轴方向上的晃动力理论值和等效力学模型的预测值均为零。

如图8所示，俯仰运动将引起较大的俯仰力矩即z轴方向的力矩，同时x轴方向的晃动力将产生一定的y轴方向晃动力矩。从y轴和z轴晃动力矩的对比结果可见，等效力学模型与CFD软件的预测结果吻合较好。y轴方向的晃动力将引起x轴晃动力矩，因此在仿真后半段出现了一定的偏差。

由图9给出的液体质心位置对比结果可见，燃油质心主要沿x轴方向运动，在y轴和z轴方向上变化较小，且等效力学模型在质心位置上同样有较为准确的预测。基于上述结果，可认为等效力学模型对该组俯仰激励下的液体动力学响应进行了较为准确的预测。

为进一步验证该模型在其他充液高度上的有效性，对同组激励下充液高度ys=0.06 m的情况进行计算。仅给出较为关心的x轴方向晃动力、z轴方向晃动力矩(俯仰力矩)和x轴方向质心变化的预测结果，对比情况如图10所示。可以看出，虽然同样存在一定的误差累积，但整体而言，等效力学模型可以对晃动方向上的作用力、力矩和质心位置进行准确预测。

图10 俯仰激励下液体动力学响应对比(ys=0.06 m)Fig.10 Liquid dynamic responses comparison under pitch excitation (ys=0.06 m)

4.2 考虑燃料消耗算例验证

对第3节中建立的变充液比等效力学模型进行验证，考虑燃料消耗过程中等效力学模型各个参数的变化。为快速验证模型有效性，假设副油箱内初始燃油体积为0.586 4 m3(充液比为80%)，单位时间内流出燃油体积0.005 m3，经过100 s仿真时间后剩余燃油体积为0.086 4 m3(充液比为11.8%)。假设飞机在燃油消耗过程中绕其重心做滚转运动，以如下两组简谐激励为例进行模型验证。

4.2.1 滚转激励(1)

滚转角γ=30°sin(0.4πt)。利用CFD软件进行仿真，期间部分时刻副油箱yz对称面上液体形态及压强分布如图11所示，可明显看到燃油的消耗过程，且燃油沿z轴有较大幅度晃动。

图11 滚转激励(1)下部分时刻液体形态及压强分布Fig.11 Liquid configuration and pressure distribution at some moments under roll excitation (1)

类似地，为验证等效力学模型的有效性和准确性，给出晃动力、晃动力矩和液体质心位置的CFD仿真对比结果。由图12所示的晃动力对比结果可见，滚转激励理论上不引起x轴方向单摆的晃动；z轴方向单摆的运动将引起y轴和z轴方向作用力的改变，且等效力学模型的预测结果与CFD软件的仿真结果吻合良好。此外，随着燃料的消耗，y轴方向上的作用力大小呈下降趋势，等效力学模型同样对这一影响进行了准确预测。

图12 滚转激励(1)下晃动力对比Fig.12 Slosh forces comparison under roll excitation (1)

由图13给出的晃动力矩对比结果和图14给出的液体质心位置对比结果可见，等效力学模型对燃油消耗和燃油晃动所引起的动力学响应都有着非常准确的预测。从力、力矩、质心位置等参数的结果都可以看到，等效力学模型的预测结果随时间即燃油消耗而平缓变化，从一定程度上验证了等效模型参数插值处理的合理性和可行性。

图13 滚转激励(1)下晃动力矩对比Fig.13 Slosh moments comparison under roll excitation (1)

图14 滚转激励(1)下液体质心位置对比Fig.14 Liquid center of mass comparison under roll excitation (1)

4.2.2 滚转激励(2)

为进一步验证模型有效性，改变滚转激励幅值和周期，令滚转角γ=20°sin(0.2πt)。仅给出与滚转激励更为相关的z轴方向晃动力、x轴方向晃动力矩(滚转力矩)和z轴方向质心变化的预测结果，与CFD仿真结果的对比情况如图15所示。可以看出，虽然CFD仿真结果存在一定的高频振动现象，但等效力学模型可以对作用力、力矩和质心位置等的变化趋势及变化范围进行准确计算。

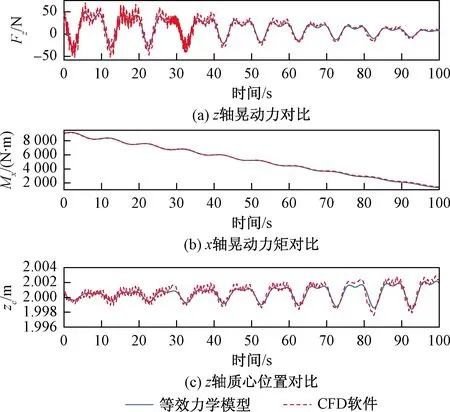
图15 滚转激励(2)下液体动力学响应对比Fig.15 Liquid dynamic responses comparison under roll excitation (2)

5 结论

以飞机副油箱为研究对象，分析燃油在油箱内的晃动行为，并基于势流理论和有限元法建立了高效准确描述燃油晃动动力学行为的单摆等效力学模型。以俯仰激励和滚转激励为例，分别以不同充液高度的固定充液比副油箱和考虑燃料消耗的变充液比副油箱为对象，对所提出的燃油晃动等效建模方法进行了验证。

通过将燃油晃动中最主要的动力学响应如对油箱的作用力和力矩、燃油质心位置变化等与CFD软件的仿真结果进行对比，验证了单摆等效力学模型的有效性和准确性，以及模型参数插值处理的合理性和可行性。该建模方法可推广至简单形状整体油箱内的燃油晃动描述，并为含防晃装置的副油箱及复杂结构机翼油箱内的燃油晃动建模提供重要参考。