基于分形的多孔介质复合相变材料的储热特性

王关皓， 庄依杰， 朱庆勇*

(1.中山大学航空航天学院， 广州 510275； 2.广东工业大学环境科学与工程学院， 广州 510006)

近年来，相变储热系统(latent heat thermal energy storage,LHTES)以其工作温度接近恒定、蓄能密度大、质量密度低和熔融温度适宜等优点而受到广泛关注，然而，相变材料(phase change material,PCM)的导热系数通常较低，这阻碍了LHTES系统的传热效率，而在LHTES使用了膨胀石墨(expan-ded graphite,EG)、泡沫金属材料和纳米颗粒等强化传热技术就能很好地解决这一问题[1-9]。

赵长颖等[10]研究了泡沫金属和膨胀石墨增强储热系统传热性能的可行性，发现这些多孔介质可以增强系统的传热性能，减少吸放热的时间。吴淑英等[11]在石蜡中添加高导热系数的纳米颗粒，形成石蜡/纳米复合相变材料。陆威等[12]将纳米铝粉加入到液体石蜡中，并利用膨胀石墨制备出了纳米铝粉/石蜡/膨胀石墨复合相变材料，并通过实验研究了其热物性能。Mesalhy等[13]采用非热平衡双温方程模型，采用准稳态导热法计算了多孔基体与PCM之间的体积相间传热系数，推导了固体基体和PCM有效导热系数的解析表达式。Harris等[14]建立了多孔介质相变过程的近似理论焓模型，该研究结果为相变前缘参数化提供了理论依据。Liu等[15]、Srivatsa等[16]分别提出了预测潜热蓄热系统和散热器中PCM相变的三维输运模型。由于多孔膨胀石墨的孔隙分布符合分形标度律，余杨敏等[17]利用分形理论来计算Li2CO3-K2CO3/EG复合材料的有效导热系数，并通过与实验值对比得出该结果正确。

膨胀石墨内部孔隙分布非常复杂，在不同的单元体积里孔隙率大小存在波动，利用三维W-M(Weierstrass-Mandelbrot)分形函数对孔隙率的波动进行修正，分析修正孔隙率和平均孔隙率对固态显热蓄热阶段LHTES中PCM熔融速率的影响，然后讨论不同的膨胀石墨孔隙和膨胀石墨与纳米颗粒-PCM的有效导热系数比对LHTES中传热速率的影响。LHTES中PCM经历固态显热蓄热、恒温的潜热蓄热过程后会进入液态显热蓄热阶段，针对该阶段讨论了不同的纳米颗粒体积分数和膨胀石墨的孔隙率对LHTES中纳米颗粒-PCM纳米流体的对流传热的影响。

1 理论模型

1.1 物理模型

对于PCM耦合热管瞬态热管理系统(图1)，将热管置于LHTES中能让热管冷凝段处于理想工作温度范围内，LHTES能有效地吸收热管在工作中放出的热量，然后释放到空气中，从而提高热管的工作效率。

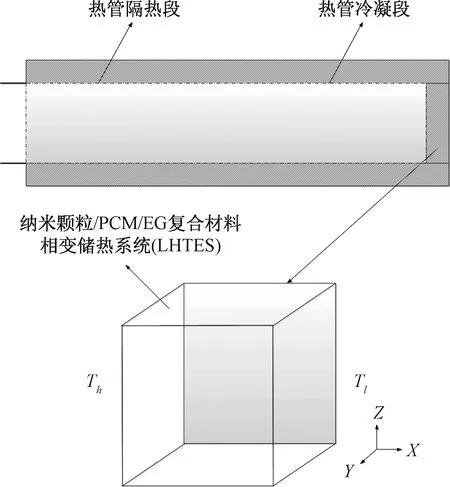
图1 物理模型示意图Fig.1 Schematic theme of the physical model

针对LHTES中纳米颗粒-PCM的传热过程进行了分析，研究区域为一个含有膨胀石墨多孔介质立方腔的立方腔，孔隙内充满了纳米颗粒-PCM材料；研究区域左壁面保持高温；右侧壁面保持低温；研究区域的其他壁面是绝热和不可渗透的。针对该模型，做以下若干假设。

(1)假设热管表面温度为常数。

(2)假设纳米颗粒为球形，从而使纳米流体的Brinkman模型和Maxwell模型是有效的。

(3)将纳米颗粒-PCM假设为连续介质，忽略热分散。

(4)熔融的纳米颗粒-PCM的流体流动是牛顿的、层流的、不可压缩的，黏性耗散可以忽略，考虑相变区域自然对流，采用 Boussinesq 近似，有：

(1)

式(1)中：(ρCp)nf、(ρCp)PCM、(ρCp)sp分别为纳米流体、PCM和纳米颗粒的体积比热容；β为温度引起的体积膨胀系数。

(5)假设纳米颗粒-PCM和膨胀石墨的热物理性质为常数，基于Boussinesq近似，纳米颗粒-PCM的密度仅为温度T的线性函数。

(6)膨胀石墨和纳米颗粒-PCM纳米流体满足局部非热平衡条件，需要两个能量方程来研究液相和固相之间的传热关系。

(7)纳米颗粒-PCM是一种含铜纳米颗粒的Li2CO3-K2CO3相变材料，铜和Li2CO3-K2CO3的热物理性质如表1所示。

表1 铜和Li2CO3-K2CO3的热物理性质Table 1 Thermophysical properties of the copper and Li2CO3-K2CO3

1.2 膨胀石墨孔隙率修正

Li2CO3-K2CO3/EG复合材料由熔盐晶体、石墨片层及孔隙3部分组成，多孔膨胀石墨的扫描电镜(scanning electron microscope,SEM)图像如图2所示。

从图2可以看出，其孔隙结构杂乱无章，用平均孔隙率很难准确地分析其对PCM相变速率的影响。用分形理论来表征膨胀石墨孔隙结构，多孔膨胀石墨的孔隙累积数目N与孔径大小λ符合以下标度律[18]：

(2)

式(2)中：Df为多孔EG的孔隙分形维数；L为尺度；λmax为最大孔隙尺寸。考虑多孔膨胀石墨中任意一点P(x,y,z)，围绕该点取一个有足够多孔隙的微元体积ΔVi，孔隙体积为(ΔVP)i，则孔隙率φi表达式为

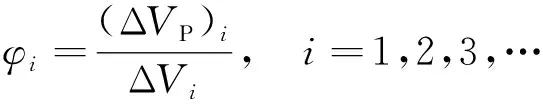
(3)

设存在一个指定大小的ΔVk，孔隙率的平均值可以用φk表示，若微元体积ΔVi<ΔVk，其中的孔隙个数减少，ΔVi的减小将会引起φi的波动。为了模拟多孔介质中孔隙率φi的波动，进而得到更加接近真实多孔膨胀石墨中流体的传热速率，引入三维W-M分形函数对多孔膨胀石墨中的孔隙率波动修正[19]为

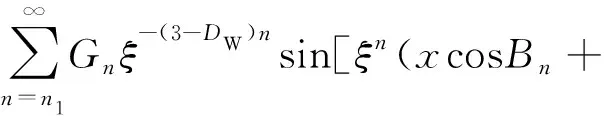
ysinBn)+zsinAn]

(4)

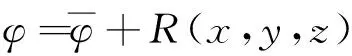
(5)

1.3 控制方程

根据以上假设，热非平衡模型的连续性方程、动量方程和能量方程表示为

(6)

(7)

(8)

(9)

式中：u=(u,v,w)T表示速度矢量；t为时间；p为压力；g是重力加速度；T为温度；η为固液相之间的体积相间传热系数，纳米颗粒-PCM的密度ρnf为

ρnf=(1-δ)ρPCM+δρsp

(10)

式(10)中：δ为纳米颗粒的体积分数。焓-孔隙度法在求解能量输运方程时可以同时跟踪相界面，纳米颗粒-PCM的体积平均焓H为

H=Cpnf(T-Tref)+flLnf

(11)

式(11)中：Tref为参考温度；Lnf为纳米颗粒-PCM的潜热；f1为液相体积分数。

在焓-孔隙度法中引入了隐式跟踪纳米颗粒-PCM固液相界面的方法，液相体积分数fl可以表示为

(12)

式(12)中：Tps和Tpl分别为纳米颗粒-PCM的凝固温度和熔融温度，从式(12)可以看出，fl与温度之间存在一一对应的关系，从而可以确定固液界面相的位置以及温度场的纳米颗粒-PCM体积分数。

LHTES中PCM进入液态显热蓄热阶段时，纳米颗粒-PCM流体的有效黏度由Brinkman模型得出，即

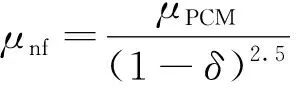
(13)

多孔膨胀石墨渗透率的分形表达式[18]为

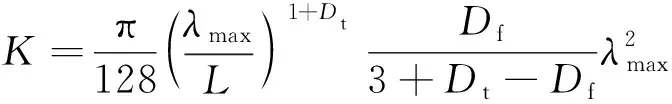
(14)

式(14)中：Dt为多孔膨胀石墨的孔隙迂曲度分形维数。根据Maxwell方程组计算纳米颗粒-PCM的导热系数knf为

(15)

式(15)中：kPCM和ksp为PCM和纳米颗粒的导热系数，在分形多孔EG中纳米颗粒-PCM流体的有效导热系数keff可以表示为[20]

(16)

利用以下无量纲参数来简化控制方程：

经过无量纲化后的控制方程变为

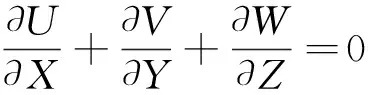
(17)

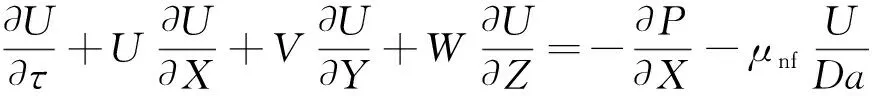
(18)

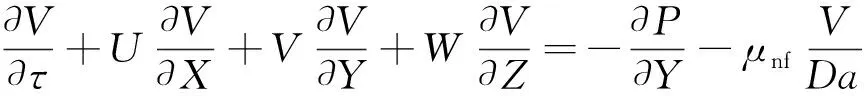
(19)

(20)

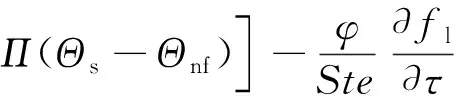
(21)

(22)

式中：Da为Darcy数；Pr为Prandtl数；Ste为Stephen数；Fo为Fourier数；γ为膨胀石墨与纳米颗粒-PCM流体的有效导热系数比；Π为无量纲的体积相间传热系数。边界条件为

(23)

传热效率可以用左壁面无量纲的平均Nusselt数表征为

(24)

1.4 数值离散

控制方程的空间项采用四阶精度有限体积法在三维交错网格上求解控制方程[21],时间项采用三阶龙格-库塔(Runge-Kutta)方法离散，即

(25)

1.5 计算程序验证

在计算之前执行一个网格无关测试：对于不同的Nunf和Nus，发现对不同的均匀网格进行了计算得到的结果误差小于1%，因此，考虑到计算的时间经济性和计算结果的准确性，选择了443的网格和10-5的时间步进行计算。

关于计算LTNE条件下的验证，表2列出了当Ra=103时不同的γ和η的情况下与Baytas等[22]关于液相和固相的平均Nunf和Nus数的对比结果。可以看出，本文数值结果与Baytas等[22]的结果相差较小。

表2 LTNE条件下结果对比Table 2 Comparison with LTNE

2 结果和讨论

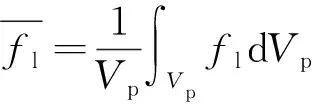
(26)

与平均熔融体积分数相比，PCM熔融过程中LHTES中所储存的能量是表征其性能的最重要因素，即

(27)

令Da=10-2，Pr=10，Ra=103，η=10，研究利用不同导热系数和不同孔隙率的膨胀石墨的效果，从膨胀石墨的平均孔隙率、修正孔隙率和膨胀石墨与纳米颗粒-PCM的有效导热系数等方面研究固态显热蓄热阶段LHTES中纳米颗粒-膨胀石墨增强PCM熔融性能，并对液态显热蓄热阶段不同纳米颗粒体积分数和膨胀石墨修正孔隙率在LHTES中的对流传热进行了对比研究。

2.1 膨胀石墨孔隙率对LHTES中熔融过程的影响

当膨胀石墨用于改善PCM在LHTES中的传热性能时，膨胀石墨孔隙率是提高储能效率必须考虑的重要因素。如上文所提，膨胀石墨内部孔隙结构分布杂乱无章，孔隙率大小在不同的单元体积有波动，因此用三维W-M分形函数进行修正。令有效导热系数比γ=80，分别选取孔隙率φ为0.8、0.85、0.9的膨胀石墨，并利用三维W-M分形函数对此分别进行修正，研究平均孔隙率和修正孔隙率对LHTES中PCM熔融过程的影响。

图3、图4显示了不同的平均孔隙率和修正孔隙率对LHTES中液相体积分数fl和能量Q的影响。

图3 不同的平均孔隙率和修正孔隙率对LHTES中液相体积分数的影响Fig.3 Effect of different average porosity and modified porosity on liquid volume fraction in LHTES

图4 不同的平均孔隙率和修正孔隙率对LHTES中能量的影响Fig.4 Effect of different average porosity and modified porosity on energy in LHTES

随着无量纲时间Fo的改变，LHTES中液相体积分数必然发生变化，可以看出，随着孔隙率的减小，膨胀石墨的热量传导的作用越发明显，纳米颗粒-PCM的熔融速度加快，而LHTES中能量也随之改变。当φ=0.8时，LHTES中能量Q在Fo=0～0.04处急剧增大，因为该时间段内由于膨胀石墨良好的传热效率，LHTES中大部分PCM已经处于熔融状态；随后Fo=0.04～0.2时，LHTES中能量基本不变。对于固定的Fo数，LHTES中能量Q随着膨胀石墨孔隙率φ的增大而减小；由于φ越大，LHTES中填充的PCM含量越多，整体传热效率较慢，处于熔融状态的PCM体积分数较小，则此时LHTES中能量Q较小。另外，对于同样孔隙率的膨胀石墨，利用三维W-M分形函数修正孔隙率的膨胀石墨在任意不同的微元体积ΔVp内的孔隙结构符合分形分布，该孔隙结构模型在一定程度上抑制了纳米颗粒的局部团聚，从而纳米颗粒-PCM在LHTES中的熔融速率加快，所以利用三维W-M函数进行孔隙率修正的LHTES中能量Q增长速率比平均孔隙率的高。

2.2 膨胀石墨孔隙率和有效导热系数比对LHTES中熔融过程的影响

膨胀石墨的孔隙率大小采用2.1节的修正孔隙率，探讨改变膨胀石墨导热系数对LHTES中熔融过程的影响。选取孔隙率φ为0.8、0.85、0.9的膨胀石墨，并且选取与纳米颗粒-PCM的有效导热系数比γ为60、80、100的基体材料，研究不同的孔隙率和有效导热系数比的耦合对LHTES中熔融过程的影响。

图5、图6显示了不同的孔隙率和有效导热系数比对LHTES中相体积分数fl和能量Q的影响。孔隙率经过三维W-M分形函数修正后，热量随着膨胀石墨基体的传导增强，根据热非平衡，选取不同的导热系数的膨胀石墨，热传导速率会有所不同。当孔隙率φ=0.8时，在无量纲时间Fo=0～0.06时，LHTES中液相体积分数fl急剧增大，热量通过膨胀石墨迅速传递给纳米颗粒-PCM，从而LHTES中能量Q也迅速达到峰值。另外，对于固定的Fo和孔隙率φ=0.8，有效导热系数比分别为γ=100的膨胀石墨比γ=60和γ=80的热传导性能更好。当φ=0.85时，LHTES中液相体积分数fl和LHTES中能量Q在无量纲时间Fo=0～0.1时处于稳定上升阶段。与此同时，有效导热系数比为γ=100和γ=80的上升速率明显比γ=60的快，并且γ=100和γ=80的最终趋势趋于一致。当φ=0.9时，液相体积分数fl和能量Q处于一直上升的趋势，由于孔隙率的增大，膨胀石墨基体的减少降低了整体系统的吸热效率，PCM熔融速率偏慢，并且不同的有效导热系数比γ之间的差异也增大，由此可见，当膨胀石墨含量开始减少时，有效导热系数比将成为影响PCM熔融速率的主要因素。

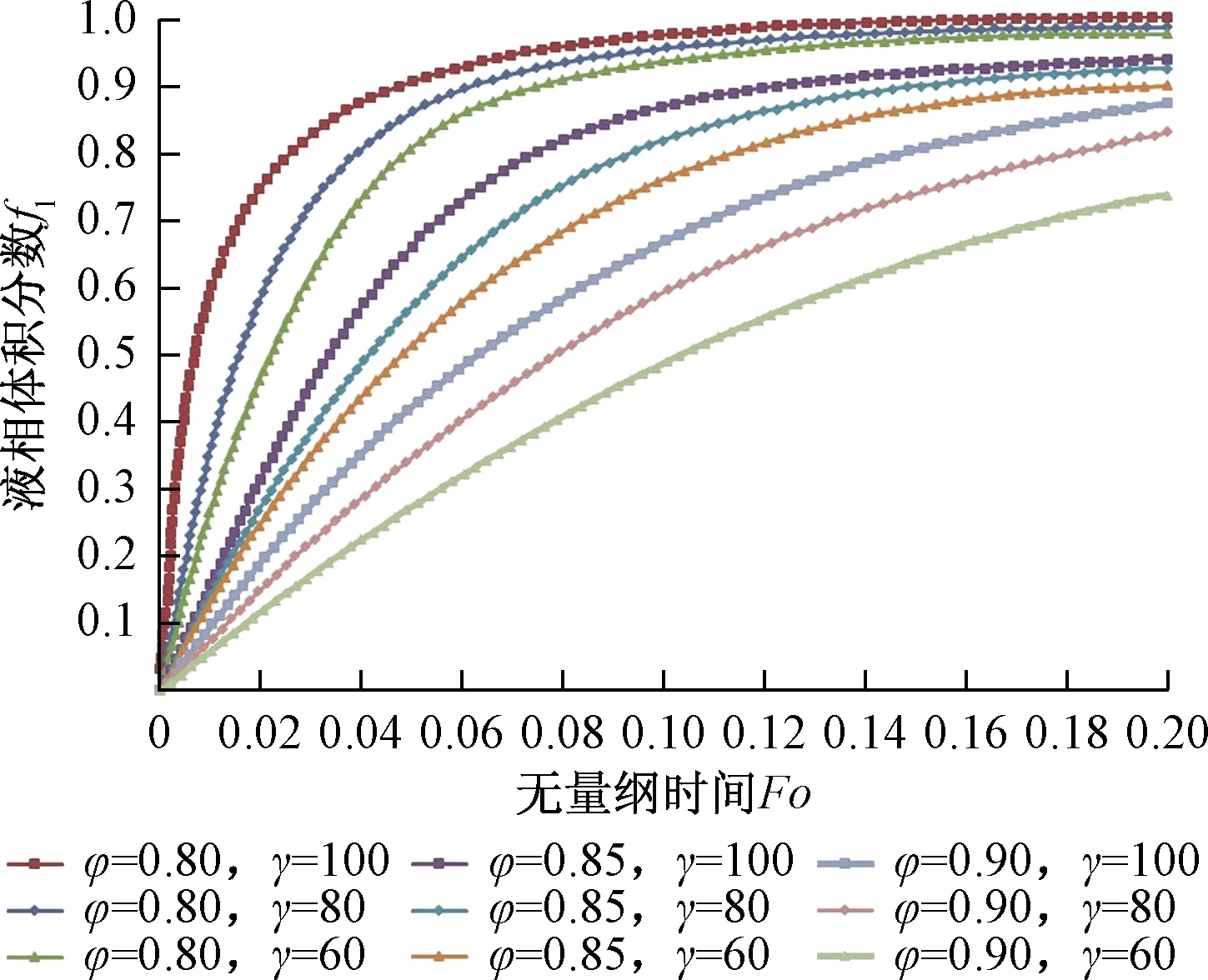
图5 不同孔隙率和有效导热系数对LHTES中液相体积分数的影响Fig.5 Effect of different porosity and effective thermal conductivity on liquid volume fraction in LHTES

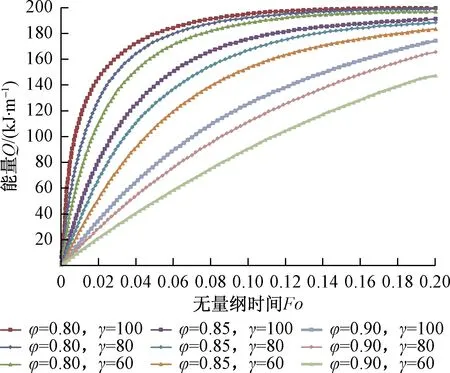
图6 不同孔隙率和有效导热系数对LHTES中能量的影响Fig.6 Effect of of different modified porosity and effective thermal conductivity on energy in LHTES

2.3 膨胀石墨孔隙率和纳米颗粒体积分数对LHTES中对流传热的影响

膨胀石墨的孔隙率大小采用2.1节的修正孔隙率，探讨不同的纳米颗粒体积分数对液态显热蓄热阶段LHTES中对流传热的影响。通过计算LHTES中的平均温度Tave可以区分PCM的固态显热蓄、热潜热蓄热阶段和液态显热蓄热阶段，即

(28)

如图7所示，当固态PCM完全融化后，温度升高至PCM熔点，此阶段为固态显热蓄热，当热源热管的温度高于PCM的熔点，PCM会经历一段恒温的潜热蓄热的过程，最后整体的温度继续升高达到热管温度，进入液态显热蓄热阶段，该阶段内液相PCM在多孔膨胀石墨内存在对流现象，膨胀石墨孔隙率和纳米颗粒体积分数是提高储能效率应考虑的两个重要因素。在PCM中加纳米铜颗粒时，纳米颗粒-PCM材料的有效导热系数有所增加，但与膨胀石墨的导热系数相比其增值较小。纳米颗粒的添加主要是由于其比表面积较大，在PCM的熔融过程中能使热量均匀分布，并且抑制了PCM固液两相界面的热阻隔。

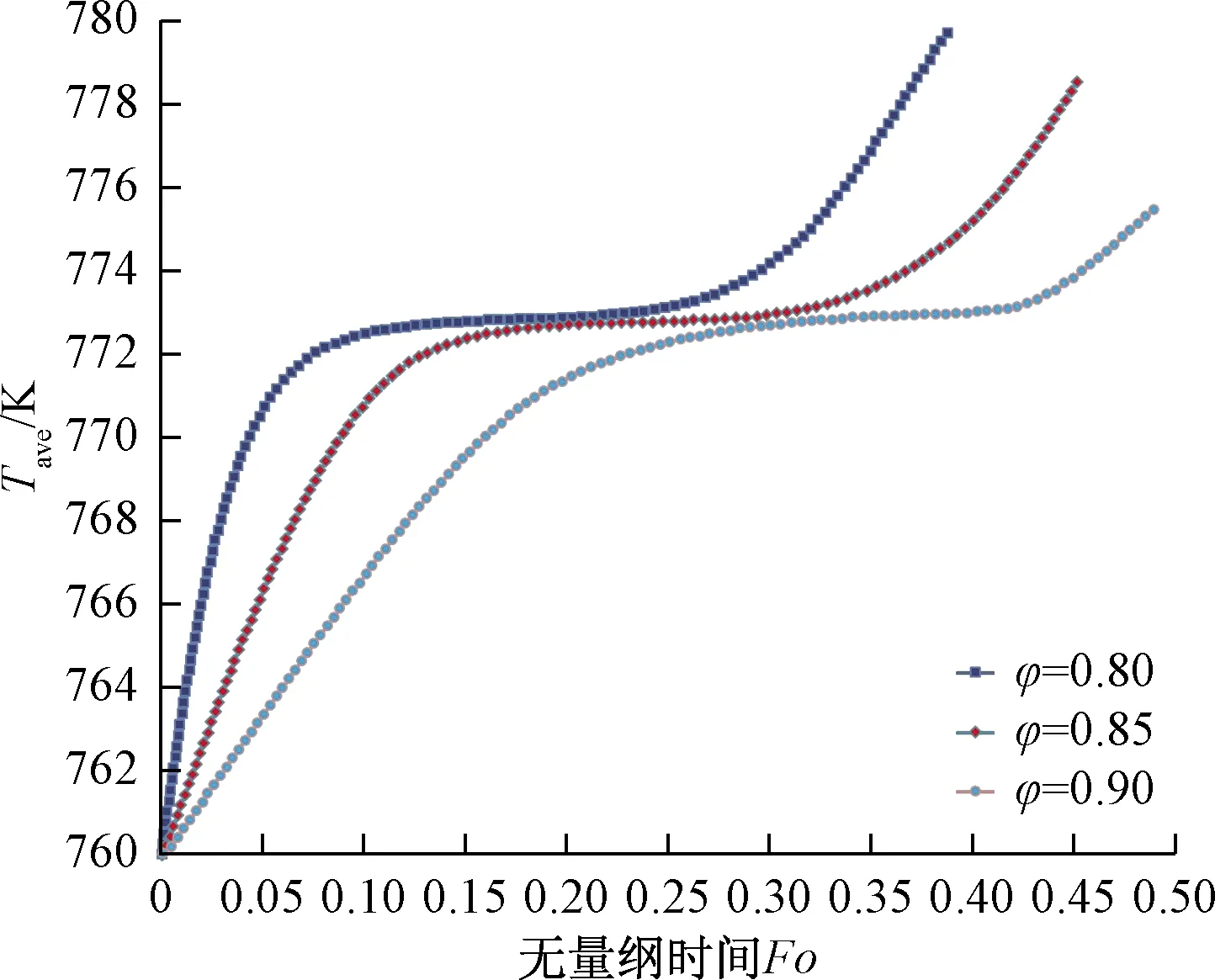
图7 相变材料温度随着无量纲时间Fo的变化Fig.7 The temperature of phase change material varies with dimensionless time Fo

令有效导热系数比γ=80，膨胀石墨的孔隙率φ为0.8、0.85、0.9，纳米颗粒体积分数δ为0、0.03、0.06，以研究膨胀石墨中纳米颗粒-PCM的对流传热过程。

图8展示了在液态显热蓄热阶段膨胀石墨孔隙率φ为0.8、0.85、0.9并且纳米颗粒体积分数δ为0、0.03、0.06的LHTES中对流等温线云图。这里使用高导热膨胀石墨的原因是为了提高PCM储能的有效导热性，从而提高能量吸收率，膨胀石墨的孔隙率越小，PCM吸收热量的速率越快。而在液态显热蓄热阶段时，随着膨胀石墨的孔隙率的增大，PCM对流传热的最大温度和浓度梯度则越大。当纳米颗粒体积分数δ=0时，孔隙率φ=0.9的等温线的斜率比φ=0.8和φ=0.85的更大，左右壁面的边界层也更薄。随着纳米颗粒体积分数δ的增大，温度的畸变在腔体中部变得愈加激烈，边界层的厚度在活动壁面附近均变小。在固定的膨胀石墨孔隙率φ=0.8下，纳米颗粒体积分数δ=0.06的左壁面温度与δ=0和δ=0.03相比出现明显的温度分层，等温线也朝着热壁面的下半部分倾斜，腔体中间区域的等温线也变得越来越弯曲，温度梯度增大。这说明纳米颗粒的存在促进了对流传热，纳米颗粒体积分数的增加会引起对流传热速率的增加。

图8 膨胀石墨孔隙率和纳米颗粒体积分数对LHTES中对流等温线的影响Fig.8 Effect of expanded graphite porosity and nanoparticle volume fraction on convective isotherm in LHTES

2.4 试验对比

在试验中，纳米颗粒-PCM是一种含铜纳米颗粒的Li2CO3-K2CO3相变材料，混合到不同孔隙率的膨胀石墨制成纳米颗粒/PCM/EG复合材料。复合材料被放置在一个绝缘空腔中，空腔的长度、高度和深度分别为100、100、100 mm，如图9所示，空腔左边是一个有外加供电电源的加热器，将加热器加热到模拟热管的表面温度，停止加热，红外摄像机记录了同一加热时间节点的温度，对记录的温度值进行算术平均，得到复合材料低温面的表面温度，误差小于0.1 ℃。将试验结果转换为纳米流体平均Nusselt数，并与不同修正孔隙率的数值模拟结果进行比较。

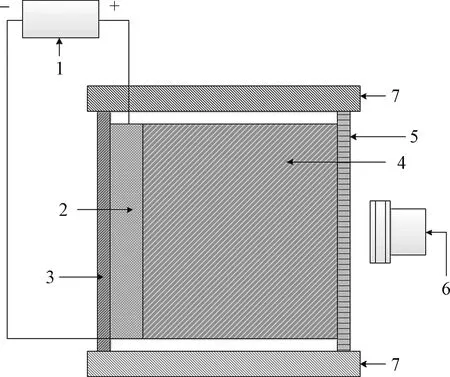
1为供电电源；2为加热器；3为隔热材料；4为纳米颗粒/PCM/EG复合材料；5为透明玻璃；6为红外摄像机；7为绝缘材料图9 试验装置示意图Fig.9 Schematic of experimental setup

图10显示了不同膨胀石墨孔隙率和纳米颗粒体积分数对纳米流体Nusselt数的影响。可以看出，在一个固定的膨胀石墨孔隙率，随着纳米颗粒体积分数的增大，纳米颗粒-PCM纳米流体Nusselt数会随之增加，并且增大幅度有减缓的趋势。纳米颗粒体积分数的增大会使流体的物性有所改变，如纳米颗粒的添加增加了流体的表面积和热容量，提高流体的导热系数。这说明通过改变纳米颗粒的体积分数可以极大地强化液态显热蓄热阶段的LHTES中纳米颗粒-PCM纳米流体传热速率。另外，通过与试验值的对比可以看出数值结果和试验结果的总体趋势一致，证明了该方法的有效性，由于试验中存在着许多影响传热效率的不可控因素，如热辐射热损失等，所以试验结果和数值结果存在一定的误差。

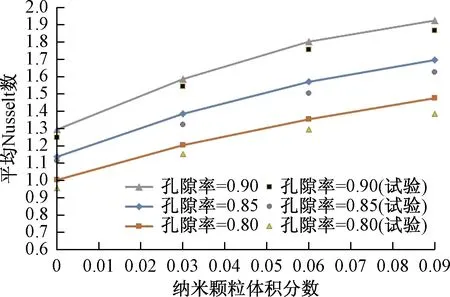
图10 膨胀石墨孔隙率和纳米颗粒体积分数对纳米流体平均Nusselt数的影响以及和试验值的对比Fig.10 Effects of porosity of expanded graphite and volume fraction of nanoparticles on average Nusselt number of nanofluids and comparison with experimental values

3 结论

利用其他已发表的数值计算结果验证本文方法的准确性，针对三维LHTES中纳米颗粒-PCM的熔融和对流传热过程进行了数值模拟，得到以下结论。

(1)利用分形理论表征膨胀石墨的孔隙结构，并引入三维W-M分形函数修正膨胀石墨孔隙率的波动，分形孔隙结构能有效地抑制纳米颗粒的自由运动，减小了纳米颗粒局部团聚的可能，因此利用三维W-M分形函数修正孔隙率的孔隙分布能更准确地模拟PCM的熔融速率。

(2)膨胀石墨孔隙率增大的同时，整体系统的有效导热系数也会减小，PCM熔融速率随之降低；对于一定孔隙率的膨胀石墨，随着有效导热系数比增大，热传导占据主动地位，则PCM的熔融速率越快；当膨胀石墨孔隙率较大时，膨胀石墨含量开始减少，有效导热系数比对PCM熔融速率的影响将变得愈加明显。

(3)在液态显热蓄热阶段，膨胀石墨孔隙率和纳米颗粒体积分数对纳米颗粒-PCM流体的对流传热速率影响较大；在固态显热蓄热阶段时，膨胀石墨孔隙率越小则PCM的熔融速率越大，而在液态显热蓄热阶段，膨胀石墨孔隙率的增大会促进纳米颗粒-PCM纳米流体的对流传热；另外，加入纳米颗粒会增加纳米颗粒-PCM流体的有效导热系数，从而促进了LHTES中纳米颗粒-PCM流体对流传热。