新型钢管脚手架外挂防护体系现场试验及承载力分析

王秀丽， 王 康， 靳立佳， 马永炯

(1.兰州理工大学土木工程学院, 兰州 730050; 2.兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 兰州 730050; 3.甘肃第三建设集团公司, 兰州 730050)

随着社会的发展，高层及超高层建筑比比皆是，在满足人们物质需求的同时也为钢管脚手架的发展开辟了广阔的天地，风荷载作为高层及超高层建筑脚手架施工技术以及施工安全的关键性因素之一，一直备受人们关注[1-6]。赵飞[7]通过附着升降脚手架在风荷载作用下的静力与动力位移响应对比分析以及在不同等级风荷载作用下的位移响应对施工带来的影响分析,提出了指导附着升降脚手架施工控制的建议。秦桂娟等[8]研究了不同高度处脚手架大横杆在风荷载作用下的效应，得到了大横杆受力变化规律，为超高层建筑施工作业平台扣件式脚手架安全合理设计提供依据。陈强[9]分析比较了在活荷载控制组合与风荷载控制组合下附着导轨式升降脚手架的最大位移和应力，得出了影响附着导轨式升降脚手架的最不利荷载组合是由风荷载控制的组合。胡长明等[10]对模板支架进行足尺试验研究，得到其极限承载力和失稳模式，发现模板支架在竖向荷载作用时，由于杆件缺陷和节点特性，横杆和剪刀撑仍然承受一定的内力，并提出了广义初始缺陷的概念。与此同时，国外在这方面也做了大量的研究，Godley等[11]通过对比二维模型和三维模型对附着式升降脚手架刚度结果产生的不同影响，得出在对脚手架进行动力特性研究时节点的半刚性是非常重要的。Beale等[12]在计算脚手架系统时考虑使用了非线性模型并对其进行了二阶几何非线性分析。Weesner等[13]对5 m高的承重脚手架做了4种不同状态极限承载力试验，得出不同尺寸的脚手架所能承担的重量，然后对试验的模型进行有限元分析，将结果和试验结果进行对比，得出了几何非线性分析得到的极限承载力数值低于特征值屈曲荷载，但与试验值相近的相关结论。

目前，脚手架防护体系主要采用的是密目网，易风化，可重复使用率低[14-17]，为了解决这些问题，提出了新型钢管脚手架外挂防护体系。但由于新型外挂防护体系兴起不久，只在小范围内使用，并没有得到推广。为此，笔者结合工程实例，将风荷载简化为集中力施加在外挂网上进行了现场试验，同时利用有限元软件ANSYS对单片外挂网进行模拟，可为高层及超高层建筑施工钢管脚手架安全合理设计提供参考。

1 研究内容

图1 新型钢管脚手架外挂防护体系Fig.1 External hanging protection system for new steel tube scaffold

2 试验研究

对新型钢管脚手架外挂防护体系进行现场试验，如图2所示。通过施加拉力，得到防护网在正常使用情况下的极限承载力，找到防护网的变形规律和应力分布规律。

图2 现场荷载试验Fig.2 Field load test

2.1 材料属性

试验所用脚手架架体由圆钢管组成，外挂防护网由方钢管作为骨架，外侧覆盖冲孔薄钢板，均采用Q235B结构用钢。具体材料属性如表1所示。

表1 材料属性Table 1 Material properties

2.2 荷载计算

风荷载标准值ωk按中国《建筑结构荷载规范》(GB 50009—2012)的方法计算，如式(1)所示。试验以B类场地为例，基本风压分别取0.3、0.4、0.5、0.6 kN/m2共4组，取高度为20、50、80、100 m，根据荷载规范取高度变化系数与风振系数，考虑到脚手架属于围护结构取体型系数为1.0，计算结果如表2所示。

表2 荷载计算Table 2 Load calculating

ωk=βgzμslμzωo

(1)

式(1)中：μsl为脚手架的风荷载体型系数；μz为风压高度变化系数，按建筑结构荷载规范取值；βgz为脚手架的风振系数，按建筑结构荷载规范取值；ωo为基本风压。

2.3 试验加载装置、测点布置和加载制度

试验共选取12片外挂网进行研究，加载装置采用本课题的发明专利[18]，如图3所示，将螺旋千斤顶和事先准备好的压力传感器放在两钢板之间，用两根钢丝绳连接钢板，通过手动螺旋千斤顶把力传到钢丝绳上，进而给外挂网施加拉力，其中拉力的水平分量为设计风荷载，拉力的竖向分量为上部外挂网的重力。试验过程中，通过贴应变片测量方钢管和卡座的应力变化情况，通过激光位移计测量外挂网的位移变化情况。具体的测点布置如图4所示。

图3 加载装置Fig.3 Loading device

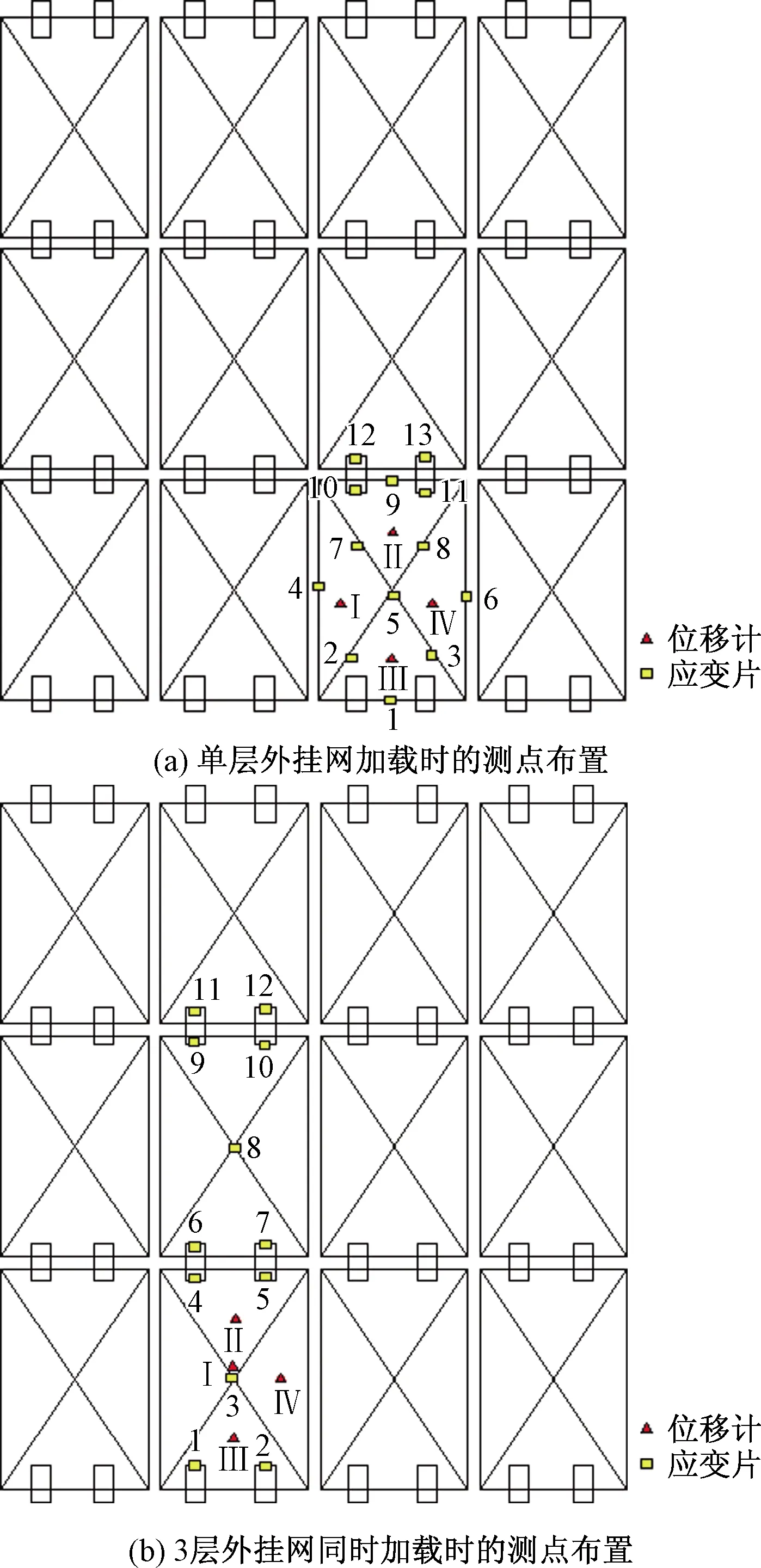
图4 外挂网测点布置Fig.4 Layout of measuring points for external hanging network

考虑到给外挂网施加风荷载的不易性，试验将风荷载等效为集中力施加在外挂网斜撑交叉处。采用分级加载，试验前先进行预加载，卸载后再正式开始试验，利用标定好的花兰螺栓和压力传感器来共同控制施加在外挂网上的力，调整千斤顶，当其达到预定值，测量并记录应变片的值，加载时每两级之间的持续时间应稳定在60 s，当快接近屈服值时密切关注应变片的值，增加持续时间，观察试验现象。

对单层外挂网进行加载时，将不同等级风荷载计算的集中力从小到大统一依次排序，将相近的集中力进行合并，先进行第1层加载试验，然后依次逐层进行试验。3层外挂网同时加载试验主要是研究风荷载沿竖向不均匀变化的特性，每层所施加的荷载代表一定高度的风荷载标准值，第1层代表高度为20～50 m，取50 m的风荷载标准值；第2层代表高度为50～80 m，取80 m的风荷载标准值；第3层代表高度为80～100 m，取100 m的风荷载标准值，依次改变基本风压进行试验，为了解外挂网正常使用情况下的性能，当每一层加载至屈服值时，停止加载。

2.4 试验现象分析

试验过程中外挂网和卡座都出现了变形。在加载过程中，随着荷载的增加，卡座和外挂网的变形逐渐增大，并且外挂网发出了“咯吱咯吱”的声音。当加载完成时，外挂网出现了较大的变形，与此同时，卡座向加载方向翘起。卸载后，外挂网恢复到初始位置，而卡座出现了不可恢复的变形，如图5所示。

京剧虽是国粹，但也不是人人都喜欢，不过受老陈每日熏陶，我对京剧唱腔也略知一二。老陈耳朵沉，他听京戏，总是把音量放到最大，这样几乎整栋楼的人都跟着他一起听。刚搬来时，我被吵得睡不着觉，就下楼找老陈。老陈耳朵沉，你说话，他总是指着自己的耳朵，说他听不见，耳朵有毛病。他一把年纪了，又不能和他吵，我只好悻悻地回去了。

图5 试验中卡座变形Fig.5 Clamp deformation in test

2.5 试验结果分析

在进行单层外挂网荷载试验时，观察到最大应力出现在卡座处，最大变形出现在外挂网斜撑交叉处。最大应力和最大位移随荷载的变化如图6所示。随着荷载的增加，最大应力和最大位移逐渐增加，当集中力为3.25 kN时，卡座进入了屈服阶段，应力值为236.7 MPa，此时，外挂网斜撑交叉处的变形量为42 mm。以测点10作为研究对象，观察不同加载位置时的应力，如表3所示，当对第1层外挂网施加荷载，应力为236.7 MPa，当对第2层外挂网施加荷载，应力为38.2 MPa，所测得的应力只有前者的16.1%，当对第3层外挂网施加荷载，应力为3.08 MPa，所测得的应力只有第1种的1.3%，每片外挂网基本上单独工作，互不影响。

图6 最大应力和最大位移随荷载的变化Fig.6 Variation of maximum stress and maximum displacement with load

表3 测点10不同加载位置的应力值Table 3 Stress value of measuring point 10 at different loading positions

对3层外挂网同时做加载试验时，发现整体可以协同工作，外挂网始终处于弹性阶段，当卸载后，均能恢复到初始位置，但卡座仍是最薄弱的环节，最大应力出现在卡座处，层与层之间的卡座都出现了不可恢复变形。

3 有限元分析

利用有限元软件ANSYS对上述新型钢管脚手架外挂防护体系进行数值模拟。试验结果发现，每片外挂网基本上是独立工作的，所以模拟时只对单片外挂网进行分析与研究。

3.1 有限元模型

对单片外挂网和连接件建立实体模型，连接件与架体的连接节点视为刚接，选择8个节点的Solid185单元作为计算单元，在外挂网和连接件接触处建立接触对，并将其附近网格细化，摩擦系数取0.15，卡座作为目标单元，类型为TARGE170，外挂网作为接触单元，类型为CONTA174。有限元模型如图7所示。

图7 有限元模型Fig.7 Finite element model

3.2 有限元结果与分析

将风荷载按照试验集中力的方式施加在模型上，荷载取值范围和试验相同，得到了最大应力和最大位移随荷载的变化，如图8所示，随着荷载的增加，最大应力和最大位移逐渐增加。当外挂网承受的集中荷载为3.25 kN时，卡座进入屈服阶段，应力为238.4 MPa，卡座出现了和试验相一致的现象，如图9所示，向加载方向翘起，外挂网出现了较大的变形，变形量为39.6 mm，位于斜撑交叉处如图10所示。

图8 最大应力和最大位移随荷载的变化Fig.8 Variation of maximum stress and maximum displacement with load

图9 有限元模拟卡座变形Fig.9 Clamp deformation in finite element simulation

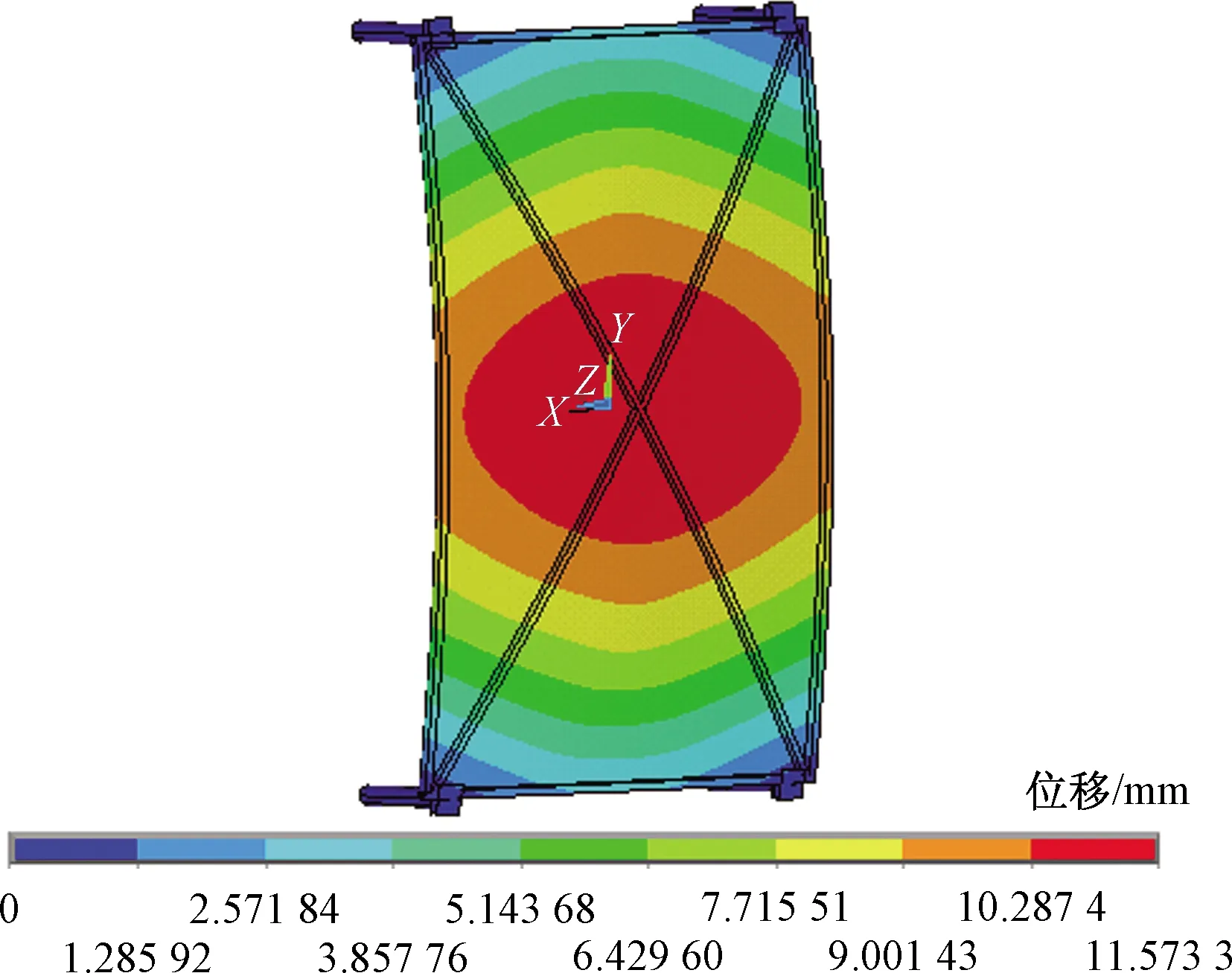
图10 集中力为3.25 kN时外挂网的变形Fig.10 Deformation of external storage network under load of 3.25 kN

将试验和模拟相对比，最大应力随荷载的变化如图11所示，最大位移随荷载的变化如图12所示，最大应力和最大位移随荷载变化的整体趋势两者相似，破坏形式两者相吻合。从图11可知，模拟所得的最大应力在每个荷载对应点处都大于试验值的，分析原因：在试验加载过程中，钢丝绳、花兰螺栓等消耗了一部分力，导致施加在外挂网上的力达不到设计值，所以所得最大应力整体偏小于模拟所得值。从图12可知，在加载初期，模拟所得的位移在每个荷载对应点处大于试验值，当荷载为1.3 kN时，试验得到的最大位移为10.2 mm，模拟得到的为13.4 mm，但是在加载后期，试验所得的位移在每个荷载对应点处大于模拟值，当荷载为3.25 kN时，试验得到的最大位移为42 mm，模拟得到的为39.6 mm，分析原因：在加载初期，由于钢丝绳、花兰螺栓等消耗了一部分力，导致施加在外挂网上的力达不到设计值，所以所得最大值整体偏小于模拟所得值，但在试验加载过程中，由于连接脚手架架体和连接件的扣件发生了滑移，如图13所示，导致加载后期的最大位移大于模拟值。

图11 最大应力随荷载的变化曲线Fig.11 Curve of maximum stress with load

图12 最大位移随荷载的变化曲线Fig.12 Curve of maximum displacement with load

图13 连接扣件滑移Fig.13 Slip of connecting fastener

4 结论

通过试验研究和有限元分析，对新型钢管脚手架外挂防护体系风荷载作用下的响应进行了研究，得到如下结论。

(1)在简化风荷载作用下，新型钢管脚手架外挂防护体系整体性能表现良好，随着荷载的增加，整体的应力和位移逐渐增加，同时，每片外挂网基本上独立工作，相互之间影响不大。

(2)通过试验和有限元分析可知，当集中荷载为3.25 kN时，卡座刚进入屈服阶段，此时，外挂网出现较大的弹性变形，新型钢管脚手架外挂网防护体系承载力不得超过3.25 kN。

(3)通过试验和有限元分析可知，在风荷载作用下，新型钢管脚手架外挂防护体系应力最大的部位是卡座，变形最大的部位是外挂网斜撑交叉处。为了使两者更好地协同工作，在进行设计时，对卡座要从厚度和高度两方面同时考虑。