穴播器混流装配线动态物料配送方法优化研究

彭慧杰 ，李成松 ，李景彬 ，朱新月

（1.石河子大学机械电气工程学院，新疆 石河子 832000；2.农业部西北农业装备重点实验室，新疆 石河子 832003）

1 引言

在稳步推进精准农业发展背景下，作为先进生产力的示范区，2017 年新疆生产建设兵团农作物精量半精量播种面积达955.6 千公顷[1]。穴播器是精量播种的关键设备之一，其多品种、小批量的混流装配模式成为播种机制造企业发展趋势。保证物料配送准确响应装配线动态物料需求变化，是提高企业装配效率的关键。

目前，国内外车间物料配送研究主要集中在配送策略、控制方法和路径优化等方面。文献[2]针对不确定环境下混装特点，提出一种和配送区间相匹配的动态周期物料配送策略。文献[3]针对混装线内部零件供应问题，提出基于线边超市的物料及时供应策略。文献[4]研究电梯零部件的物料管理与跟踪问题，提出一种基于无线射频识别的立体化仓储物料管理方法。文献[5]基于在复杂产品装配过程中的时间、效率和追溯需求，提出了一种基于条码的物流控制技术。文献[6]针对物料配送准时化需求的路径优化问题，建立数学模型并设计具有较快收敛速度的改进蚁群算法。

以上学者研究的问题规模及其所针对的环境有所区别，导致上述成果并不能完全适用于传统小微农机装备制造企业。针对穴播器混装线多品种、小批量生产方式亟待解决的物料配送问题，拟综合考虑配送策略、控制方法和路径规划，对装配线动态物料配送方法进行优化研究。开发一种拉动式动态物料联合配送方案，构建路径优化数学模型并设计遗传算法求解，最后实例验证模型的正确性。

2 动态物料配送方案

2.1 物料分类

物料分类是库存管理和物流配送的前提，不同物料的配送策略有所不同。分析穴播器BOM 表，根据混流装配线物料特点将其分为序列件和非序列件两种。标准件等体积小重量轻的物料称为非序列件，一般成箱成盒配送；不同型号产品之间有差异的物料称为序列件，应结合生产排程配送。序列件是配送重点，为保证配送方案完整，分别考虑领料和补料两个过程。开工之前，工位线边库存为零，需进行领料活动。装配过程中，当工位线边库存降至物料请求点后，拉动补料过程。每个生产周期内可能会发生多次物料配送，每个配送周期由一个领料过程和多个补料过程组成，如图1 所示。

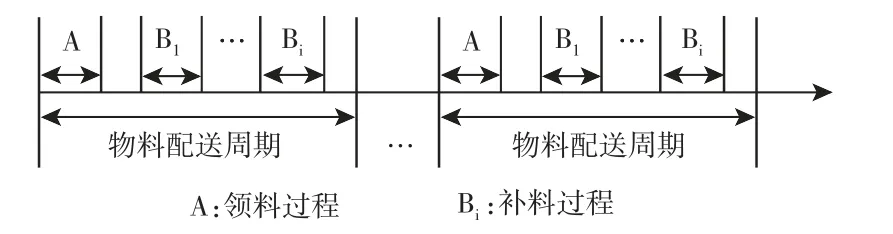
图1 物料配送周期Fig.1 Material Delivery Cycle

2.2 动态配送方法

2.2.1 领料配送策略

领料过程发生在生产准备阶段，是物料配送周期的开始，应结合排产情况、物料BOM 表与线边库存容量等确定不同类型序列件的领料数量。

以穴播器混流装配线为例进行说明，混装线可装配五种不同型号的穴播器 X7，X8，X9，X10，X15，每个产品装配 1 个腰带（序列件），其型号分别为 Y7，Y8，Y9，Y10，Y15。假设工位线边库存最大容量为10，某阶段穴播器的排产结果为：X7X7X8X8X9X10X10X10X15X7，则领料过程物料配送具体数量如下：3 个 Y7，2 个 Y8，1 个 Y9，3 个Y10，1 个 Y15。

2.2.2 补料配送方案

补料过程较领料过程更为复杂，现有研究关于物料的补充方式主要有单一物料单独补充和多类物料联合补充两种，拟研究一种拉动式的动态物料联合配送方案。

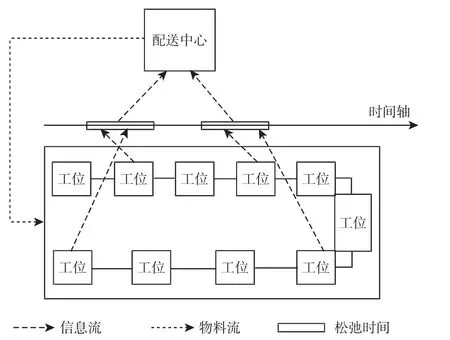
图2 补料配送策略Fig.2 Feed Distribution Strategy

补料配送策略，如图2 所示。装配时，当有工位线边库存到达补料请求点时，率先拉动补料过程。补料请求点为定值，在数值上等于订货提前期内的物料消耗量与该物料松弛时间内的消耗量之和。在松弛时间内，收集该补料周期内其他工位补料请求信息，进行联合配送。为避免装配线停产，规定最晚到货时刻为线边库存恰好完全消耗。补料过程配送的物料数量是一个区间值，其最小数量应满足：补料后该工位能装配的产品数与领料后最早拉动物料请求工位的线边库存能装配的产品数相同；其最大数量应满足：补料后该工位线边库存饱和。在该动态物料联合配送方案中，拉动补料过程的唯一条件是最早物料请求工位的线边库存降至物料请求点，保障配送有序进行。

工位线边库存变化，如图3 所示。在物料配送周期中，工位线边库存在领料过程结束瞬间饱和。随着装配进行，物料消耗，线边库存降至物料请求点，拉动补料过程。在松弛时间内收集其他补料请求信息，到达订货提前期，线边库存降至订货提前期内物料消耗量。补料过程结束，线边库存数量位于卸货后物料必须达到的最小点和最大线边库存之间。

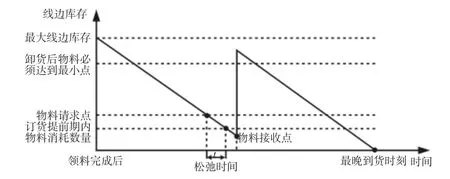
图3 装配工位线边库存变化Fig.3 Change in Line Side Stock of Assembly Station

3 问题描述与数学模型

3.1 问题描述

穴播器混流装配线动态物料配送问题可描述为：在车间物料存储区和装配线多个工位之间，规划合适的行车路径，使搬运车辆以一定的顺序依次经过他们，在满足一定约束条件的基础上，达到既定目标。为避免混装线因工位线边库存耗竭而导致停产，需严格限制物料的最晚到达时刻，此类配送问题属于有时间窗限制的车辆路径问题。穴播器车间物料配送影响因素较多，需制定合理的优化目标与约束条件。

（1）优化目标

为使配送效率最高且成本最低，拟对多个物料联合配送，故选取动态物料联合配送方案的具体优化目标为以下两个：

①车辆运输时间最短化；

②搬运车辆数量最小化。

（2）约束条件

为使混装线补料方案更符合生产实际，同时提高动态物料联合配送方案的有效性，设置约束条件应满足以下五点：

①车型约束：车间内搬运车辆只有一种类型；

②行程约束：车辆从物料存储区起止；

③数量约束：工位接收物料不得超过最大线边库存；

④装载约束：车辆每次配送物料数量总和不得超载；

⑤时间约束：设单边硬时间窗，限制最晚到货时刻。

3.2 数学模型

设定每个物料请求工位仅需一种序列件，物流点集合D=｛0，1，…，n｝，其中 0 表示物料存储区，1，…，n 表示相关工位。物料存储区和各工位之间节点坐标矩阵D，如式（1）所示。

车间有充足的搬运车辆可进行物料配送，车型最大装载量为常量q。工位i 配送的物料数量为决策变量qi（1，2，…，n），其不得超过车辆最大装载量，取值范围为［qimin，qimax］。已知每出动一辆搬运车辆的固定成本为C1，单位距离的变动成本为C2。一种物料只允许通过一台车辆配送，每一次配送过程必须在最晚到货时刻之前结束。

（1）目标函数，如式（2）所示。

（2）约束条件如下所示：

式中：yik—0-1 变量，当工位 i 由车辆 k 配送时为 1，否则为 0；xijk—0-1 变量，当车辆 k 经过工位 i 到达 j 时为 1，否则为 0；qi—工位i 配送的物料数量；q—车辆最大装载量；m—补料过程需要的车辆数；W—生产节拍；Ni—某个产品需要物料i 的数量；Si—物料i 的物料请求时刻；Ui—物料i 拉动补料过程时，对应工位线边库存可装配产品数；Sik—车辆k 将物料i 运输至所需工位的时刻；Q—领料过程完成时，最早物料请求工位线边库存可装配的产品数量；Qimax—物料i 所需工位线边库存最大时可装配的产品数量；dij—工位i 与j 之间的距离；tij—工位i与j 之间的运输时间；α—足够大的数；bi—物料i 的最晚到货时刻；qimin—物料i 的最小配送数量；qimax—物料i 的最大配送数量。

式（3）约束搬运车辆数量；式（4）约束所有物料都有车辆配送；式（5）和式（6）约束每种物料能且仅能被一辆搬运车辆配送；式（7）约束各车辆的装载量不超载；式（8）约束车辆搬运路线的连贯性；式（9）约束搬运车辆以合理的时间按顺序依次到达各工位；式（10）约束搬运车辆满足工位的时间窗限制；式（11）约束物料的配送数量范围；式（12）与式（13）约束物料的最小和最大配送数量；式（14）约束物料的最晚到达时刻；式（15）约束消除子回路。

4 基于遗传算法的模型求解

4.1 算法概述

VRP 模型是典型NP 难问题，主要有精确算法和启发式算法等求解方法，精确算法因自身特性而不适用于求解大规模问题。启发式算法是基于直观或经验构造的算法，在可接受的时间和空间下给出组合优化问题的可行解。遗传算法是元启发式算法之一，在车辆路径问题中的应用较为丰富。

4.2 遗传算法设计

4.2.1 编码

拟采用顺序编码方式，实际为三段式编码，分别为：车辆数、配送工位和车辆编号。染色体个体的编码方式，如图4 所示。车2配送工位 4，2，3，车 1 配送工位 1，5，6。

图4 染色体编码方式Fig.4 Chromosome Coding

4.2.2 适应度函数

适应度是度量种群个体质量的指标，遗传算法的关键在于判据的选取。遗传算法要求适应度函数取正值，由于目标函数为求最小值，故取其倒数作为适应度函数，即Fit=1/F。

4.2.3 遗传算子操作

选择：为避免搜索获得局部最优解，在采取最优保存策略的基础上结合轮盘赌法进行遗传算子的选择操作。

交叉：为避免出现非法染色体，主要对第二段编码进行交叉操作。在种群中随机选择两个染色体为父本，并任选一个区域交叉，得到子代1 和子代2。

变异：为改进算法的全局搜索能力，对配送顺序和搬运车辆的编码进行变异操作。配送顺序的变异可在染色体第二段中随机选取两点进行调换，搬运车辆的变异可在染色体第三段中随机选取一个车辆编号更改为另一个可行编号。

4.2.4 终止

终止条件一般为预先设定最大遗传代数的方法，当算法迭代到最大代数时终止计算，一般取迭代次数为（100～1000）。

5 实例验证

以R 农机装备制造企业穴播器混流装配线为研究对象，实例验证动态物料配送方法的有效性。该装配线共有10 个工位，1个物料存储区和3 台搬运车辆，每个物料请求工位需1 种序列件，生产节拍为259.8s。车辆装载量为60，以1m/s 的速度匀速行驶。每辆车运输的固定成本为10，每运行1m 的变动成本为1。在某补料周期内，穴播器混装线共有6 个工位发出了物料请求，工位节点坐标矩阵，如式（16）所示。工位0 为物料存储区即配送中心，其坐标为（0，0）。

工位物料相关信息，如表1 所示。工位1 最早发出物料请求，松弛时间259.8s，即所有工位补料在一个周期内。

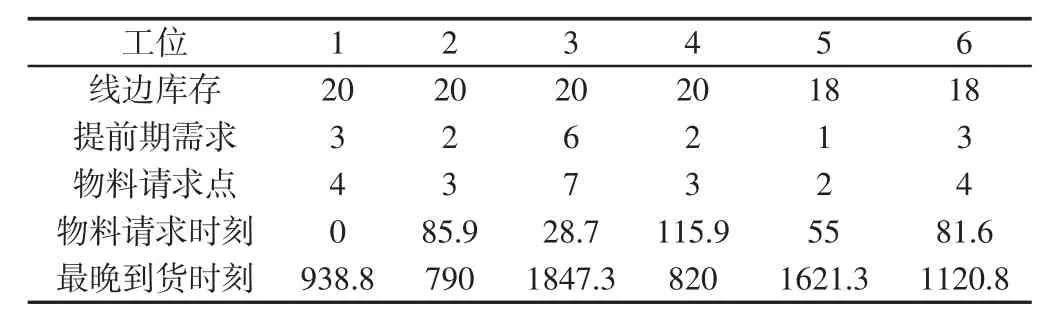
表1 工位物料相关信息表Tab.1 Station Material Related Information

采用Matlab 遗传算法求解，取种群规模100，最大遗传代数200，交叉概率0.9，变异概率0.05。随机运行10 次，最优成本为94.3，行驶距离为74.3，需2 辆车进行配送。车辆运行结果，如表2所示。物料配送结果，如表3 所示。遗传优化过程，如图5 所示。车辆行驶轨迹，如图6 所示。从结果可知，物料实际配送数量与到货时刻均满足相关约束，且车辆的装载率也较高，验证了动态物料配送方法的正确性，该结果可供现场物料配送参考。

表2 车辆运行结果表Tab.2 Vehicle Operation Results

表3 物料配送结果表Tab.3 Material Distribution Results

图5 遗传优化过程Fig.5 Genetic Optimization Process

图6 车辆行驶轨迹Fig.6 Vehicle Trajectory

6 结论

针对穴播器混流装配线多品种、小批量生产方式亟待解决的物料配送问题，重点研究序列件领料和补料两个过程的配送方法。设计了一种一次配送能满足多个工位需求的动态物料联合配送方案。建立了以车辆数量最少、行驶时间最短为目标，带单边硬时间窗等约束的车辆路径问题数学模型，并设计遗传算法求解。实例验证表明，工位实际配送物料数量和到达时刻均满足约束条件，说明模型正确且算法有效。