间隙比对近壁单圆柱绕流影响的PIV 实验研究
周 磊 ,许 慧 ,喜冠南
(1.南通大学机械工程学院,江苏 南通 226019;2.江苏大学汽车与交通工程学院,江苏 镇江 212013;3.扬州大学水利与能源动力工程学院,江苏 扬州 225127)
1 引言
流体的流动在近壁区域产生边界层[1],边界层的出现会导致近壁区域的传热效率降低,而在近壁插入圆柱能强化近壁区域的传热。为了阐明近壁圆柱绕流的流动特性对传热强化的影响,对近壁单圆柱绕流模型进行了实验研究。
关于近壁圆柱,前人已经做过一些研究。文献[2]对近壁插入单圆柱绕流进行了二维数值模拟研究,指出了近壁插入圆柱能提高传热效率;文献[3]实验研究了湍流状态下单圆柱绕流,分析了间隙比和壁面边界层厚度是影响圆柱绕流尾迹结构的主要参数。文献[4-6]实验研究了湍流状态下近壁插入串列及并列圆柱,指出间隙比和间距比是影响圆柱尾流的重要特征参数。文献[7]通过实验研究,总结了湍流状态下单圆柱绕流的三种流动模式:当间隙比较小(0~0.5)时,旋涡脱落被抑制;当间隙比中等大小(0.5~1.0)时,有周期性的卡门涡脱落,尾迹不对称;当间隙比足够大时(1.0~),尾迹逐渐对称,壁面效应可以忽略。文献[8]基于复合网格系统的计算方法,研究了近壁插入圆柱流场的瞬时传热特性,并确定了Re=200 情况下圆柱的最佳插入位置。文献[9]基于数值模拟分析了雷诺数为200、间隙比为1.0 这一工况下单圆柱与双圆柱的流动传热特性,解释了圆柱影响壁面传热强化的根本原因。文献[10]基于数值模拟分析了间距比对壁面传热强化的影响,并指出随着间隙比的增大,壁面的传热效果逐渐减弱。
总体来说,关于近壁圆柱绕流的实验研究,大多是在湍流的状态下进行的;对于过渡流,仅有一些模拟的探索,缺乏实验的验证。而且在过渡流状态下,流动具有周期性的流动不稳定性,研究过渡流下近壁圆柱有着重要意义。针对上述情况,选取雷诺数为200 的工况,对不同间隙比下近壁单圆柱绕流进行了实验研究。
2 实验装置介绍
2.1 实验台简介
实验台由上水箱1、调速阀2、整流段3、大蜂窝器4、收缩段5、小蜂窝器 6、试验段 7、过渡段 8、水箱 9、水泵 10、下水箱 11 组成,如图1 所示。其中,实验段材料为亚克力板,实验采用水为介质,循环过程分为引流和循环两个阶段。引流:水泵将水从下水箱11 引至上水箱1,上水箱的水经调速阀2 流至整流段3,并经过大蜂窝器的整流流至收缩段5,此时水流再经收缩加速流至小蜂窝器6 进行二次整流,此时流出的水均匀稳定,符合实验要求,即完成引流阶段;循环:水流经过试验段7 流至过渡段8,过渡段与实验段的比值为3:1,从而避免了回流对实验段的影响。最终,经过过渡段8 的水流至下水箱11,完成整个循环过程。

图1 开式循环水槽示意图Fig.1 Schematic Map of Open-Loop Recirculating Water Tunnel
2.2 PIV 装置简介
本实验采用的是美国TSI 公司生产的二维粒子图像测速仪,即 Particle Image Velocimetry(PIV)。PIV 装置由冷却器、激光器、CCD 相机、同步控制器、计算机以及控制软件等组成,装置工作原理如下所述,如图2 所示。

图2 PIV 测速示意图Fig.2 Schematic Map of Velocity Measurement About PIV
激光器经导光臂打出垂直于水面的片状光,并由安装于实验台正前方的CCD 相机拍摄激光照射区域。由同步控制器协调激光器与相、度矢量图。实验开始前,须在水中加入适量的示踪粒子,本实验采用的是直径为13μm 的镀银玻璃球,利用其较好的跟随性、反光性特点,显示水流的流动特性。
2.3 实验模型简介
实验模型,如图3 所示。雷诺数的计算公式为:

式中:D—圆柱直径;U0—流体进口速度;υ—运动黏性系数;C—圆柱下底面距壁面的距离;Xup—圆柱中心距上游的距离;Xdown—圆柱中心距下游的距离;H—水面高度;C/D—间隙比。在本实验中,雷诺数取200,水面高度H 为275mm,水温为20℃,圆柱直径为20mm,圆柱距上游距离为700mm。取 C/D 为 0、0.2、0.4、0.6、0.8、1.0 这 6 种工况分析近壁单圆柱绕流的流动特性。
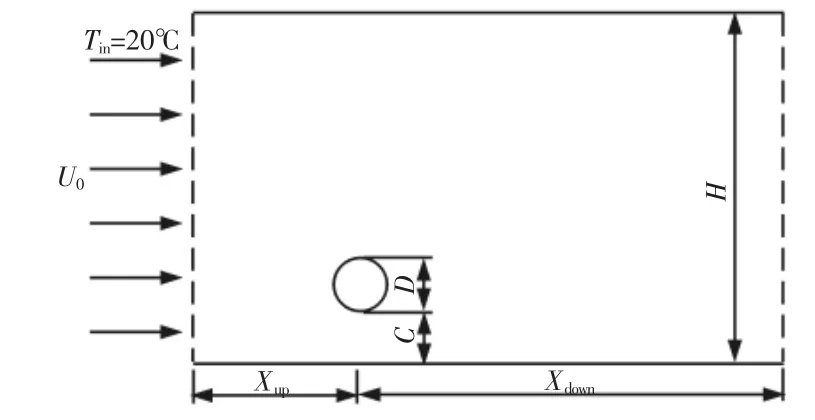
图3 实验模型示意图Fig.3 Schematic Map of Experimental Model
3 结果分析
为了研究C/D 对近壁单圆柱绕流的影响,结合速度流线、速度截面以及周期图对不同工况下时均流动特性和瞬时流动特性进行了系统的分析。
3.1 时均流动特性
从时均的角度研究流动机理具有一般性,首先对其进行了分析。为不同C/D 下间隙比下时均流线及速度场图,如图4 所示。在时均速度场中,流动特征的变化主要表现为圆柱尾迹旋涡的形态、尺度变化以及分离剪切层的形态变化。

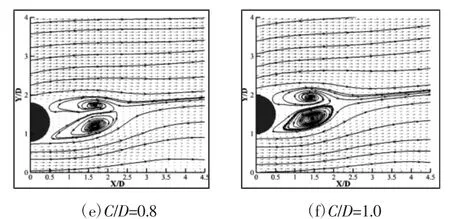
图4 Re=200 时不同间隙比下时均流线及速度场图Fig.4 Time-Mean Streamlines and Velocity Fields for Different Gap Ratios at Re=200
具体来看,速度矢量的方向为粒子该瞬时的运动方向。当C/D 为0 时,圆柱贴着壁面,来流经过圆柱壁面形成单侧的分离剪切层。随着分离剪切层的发展,圆柱尾流形成了顺时针旋转的正涡,且尺度较大。当C/D 为0.2 时,来流经过圆柱壁面形成双侧的分离剪切层。随着上游分离剪切层的发展,圆柱尾流形成了顺时针旋转的正涡;但由于间隙较小,下游分离剪切层的发展受到抑制,下游旋涡中心出现在圆柱下游不远处,且旋涡下游流体产生波动。当C/D 为0.4 时,壁面的抑制作用减弱,圆柱下游剪切层得到缓慢发展,上下游旋涡中心趋于对称。当C/D 为0.6 时,壁面的抑制作用继续减弱,上下游分离剪切层得到发展,旋涡尺度增加,旋涡下游流体的波动减弱。当C/D 继续增大至0.8 时,壁面的影响迅速下降,旋涡尺度明显减小,圆柱尾流旋涡对逐渐趋于对称。当C/D 继续增大,圆柱尾流旋涡形态与0.8 类似,并且最终趋于对称,与单圆柱情况类似。
为了进一步阐明时均流动特征变化的形成机理,下面结合时均截面速度分布进行分析。不同C/D 下的截面速度分布图,三个截面的位置分别位于X/D=1、2.5、4 处,如图5 所示。
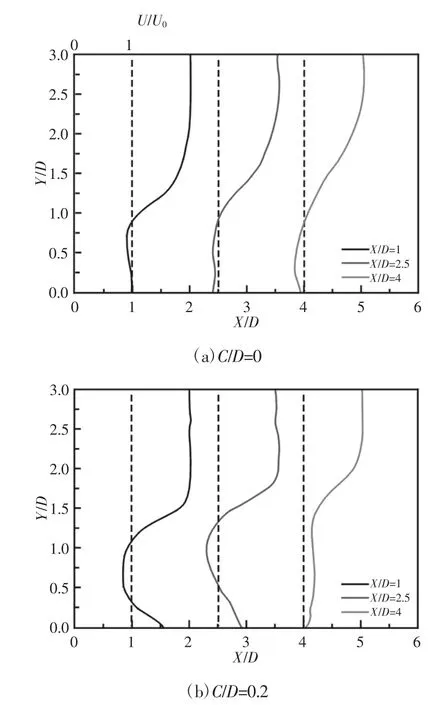

图5 Re=200 时不同间隙比下截面速度图Fig.5 Time-Mean Velocity in Cross Section for Different Gap Ratios at Re=200
当C/D 为0 时,在X/D=1、2.5 的位置处,近壁区域的流体速度趋近于0,在X/D=4 的位置处,近壁区域的流体速度出现负值。而在圆柱上游,出现了单侧的分离剪切层,由于该分离剪切层的单独作用,形成了顺时针旋转的正涡。
当C/D 为0.2 时,在X/D=1 位置处,近壁区域的流体速度迅速增加。这是因为近壁区域有流体流过,壁面边界层局部受到破坏。但是在截面4 的位置处,近壁流体的速度减弱,加速效应受到抑制。这是由于壁面边界层的再发展,导致加速效应只在圆柱后的局部区域内形成。由于壁面的作用,经过壁面的流体逐渐往右上方流动,诱导形成逆时针运动旋涡,结合上游分离剪切层的影响,上游旋涡的尺度比下游旋涡的尺度要小。
当 C/D 为 0.4 时,在 X/D=1、2.5、4 的位置处,近壁区域的流体速度略微增加,这是由于在该间隙比下,圆柱下方的流体仍受壁面边界层影响,圆柱尾流旋涡的形态与0.2 类似。
当 C/D 为 0.6 时,在 X/D=1、2.5、4 的位置处,近壁区域的流体速度明显增加,尤其在X/D=4 位置,流体速度增加明显。这是因为间隙比的增加使得近壁边界层的影响减弱,从而导致圆柱尾流速度增加,壁面边界层受到破坏的区域增大,加速效应维持的区域增大。
当C/D 为0.8 时,在X/D=1 的位置处,近壁区域的流体速度继续增加,此时达到临界值,即圆柱下游流体的速度等于上游流体的速度。这是因为在此间隙比下,圆柱下游的流体已经脱离了壁面边界层的影响,下游流体的速度增大至上游流体的速度,从而导致了圆柱尾流的旋涡尺度大幅减小。而且在截面4 的位置处,圆柱尾流的速度大小明显回复。
当 C/D 继续增大至 1.0 时,在 X/D=1、2.5 的位置处,截面的速度没有发生明改变。此时壁面的影响已经很小,圆柱尾流的旋涡形态表现为对称,圆柱后方速度完全回复。
总体上,C/D 的改变主要能影响圆柱与壁面的相互作用,从而引起不同形态的分离剪切层、加速效应、尾流旋涡的形态以及速度回复。具体来看,随着间隙比的增大,两侧剪切层的发展趋于对称,尾流旋涡尺度逐渐减小,加速效应先增强后减弱,尾流速度回复效应加快。
3.2 瞬态流动特性
瞬时速度场能够反映真实的流动形态,为了从瞬时的角度说明不同C/D 对圆柱尾流形态的影响,以下结合瞬时流线速度场进行分析。为不同C/D 下瞬时流线及速度场图,如图6 所示。在瞬时速度场中,流动特征的变化主要表现为圆柱尾流的形态变化、尺度变化以及近壁区域的流动特征。

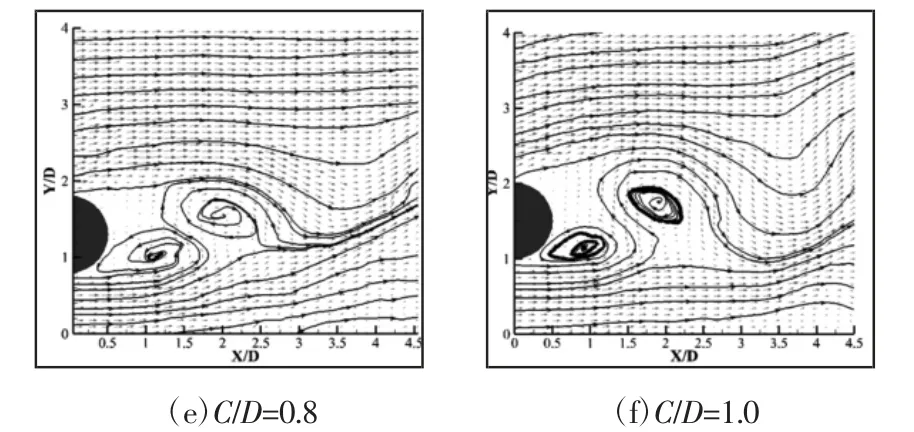
图6 Re=200 时不同间隙比下瞬时流线及速度场图Fig.6 Instantaneous Streamlines and Velocity Fields for Different Gap Ratios at Re=200
当C/D 为0 时,圆柱尾流在X/D=3 的下游形成顺时针旋转的大尺度正涡,在X/D=0 与X/D=3 之间形成死区。当C/D 为0.2时,来流经过圆柱壁面形成双侧的分离剪切层。由于间隙较小,下游分离剪切层的发展受到抑制,使得分离剪切层提前分离,形成两个逆时针旋转的负涡并向上凸起。由于下游剪切层的影响,上游剪切层发展受到抑制,尺度较小。当C/D 为0.4 时,壁面的影响减弱,下游旋涡凸起效果减弱,上游旋涡尺度逐渐增大。当C/D 为0.6 时,由于C/D 的增大,下游分离剪切层受到的抑制作用减弱,圆柱下游的两个小涡合并为一个逆时针旋转的正涡,结合上述速度场分析,此时壁面的扰动明显增强。当C/D 继续增大至0.8,上游分离剪切层依旧形成一个顺时针旋转的正涡;但下游分离剪切层受到壁面的抑制减弱,两侧剪切层的共同作用促使速度回复效应增强,圆柱尾流形成逆时针旋转的负涡,旋涡尺度明显减小。随着C/D 继续增大至1.0,圆柱尾流的形态与0.8 类似。
从以上分析可以看出,间隙为0.6 时壁面的扰动较为强烈,为了进一步理清间隙比为0.6 时壁面的扰动情况,以下对其一个周期内圆柱尾流的流动特性进行分析。
为Re=200 时一个流动周期内不同瞬时的流线及速度场图,如图7 所示。一个和另一个箭头标记的分别是旋涡A、旋涡B,圆柱尾流的扰动表现为多个旋涡的交叉运动。旋涡A 从出现开始,慢慢往下游移动并且旋涡尺度不断增大,旋涡B 也伴随着出现、增强、脱落三个过程。随着旋涡的脱落,圆柱尾流出现明显的摆动,这种周期性的摆动增强了近壁区域的流动不稳定性。

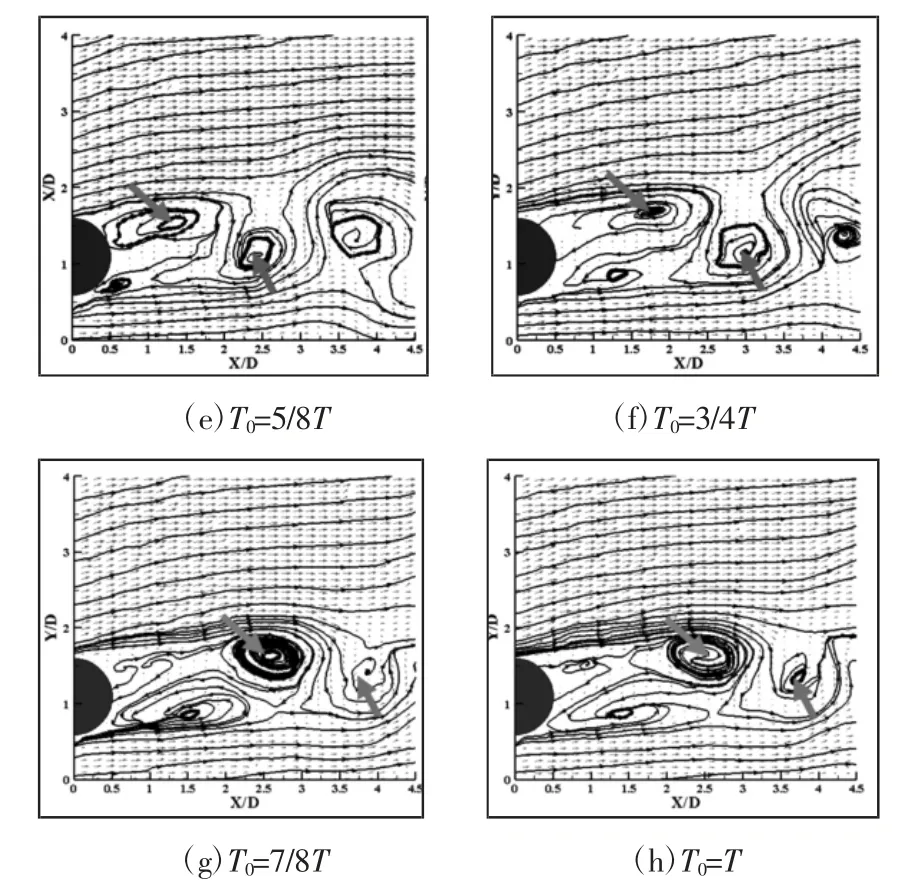
图7 Re=200 时一个流动周期内不同瞬时的流线及速度场Fig.7 Streamlines and Velocity Fields for Various Time Instants of the Periodic Cycle at Re=200
总体上,随着C/D 的增大,圆柱尾流的流动状态由初始的单个旋涡逐渐演变为旋涡对,旋涡尺度逐渐减小,近壁区域的流动不稳定先增强后减弱。
4 结论
在Re=200 的情况下,圆柱尾流的流动形态与间隙比的变化有关,具体总结如下:(1)间隙比对近壁圆柱绕流的流动特性影响显著。间隙比的改变主要影响圆柱与壁面的相互作用,从而引起不同形式分离剪切层以及尾流旋涡形态的变化。(2)随着间隙比的增加,尾流的流动形态由单个旋涡逐渐演变为旋涡对,旋涡尺度逐渐减小,并且近壁区域的流动不稳定性先增强后减弱。(3)间隙比仅在一定范围内对圆柱尾流产生影响。根据所研究的工况,在C/D<0.6 时,壁面对圆柱尾流的影响较大,加速效应明显,壁面扰动增强;在C/D>0.6 时,壁面对圆柱尾流的影响较弱,圆柱尾流的旋涡尺寸对称,并出现明显得速度回复。

