罗德里格斯旋转公式的证明及应用
刘 锋
(湖南工学院,湖南衡阳421002)
0 引言
在刚体旋转问题中,有很多不同的方式表示刚体旋转后的姿态,例如旋转矩阵、欧拉角、四元数和轴角表示法。
其中轴角表示法中只要知道旋转轴和旋转角就可写出刚体的姿态矩阵。轴角表示法来源于欧拉定理:刚体作定点运动的任何位移都可以通过绕固定点的某个轴的一次转动实现。欧拉定理等价于旋转矩阵有等于1 的特征值,其对应特征向量x就是表示旋转轴的方向。
1 轴角表示法和罗德里格斯公式
假设刚体坐标系为B(Oxyz)绕单位向量ω所表示的轴旋转θ角,可以推导出其对应的旋转矩阵。首先假设刚体坐标系B的z轴与ω所表示的任意轴重合,然后B坐标系绕参考坐标系A(OXYZ)的Z轴旋转-α角使z轴在XOY平面的投影与X轴重合,然后再绕-β角,使z轴和Z轴重合,接着绕Z轴旋转θ角,最后为了使z重新回到与ω轴重合的位置,可以绕Y轴旋转β角和绕Z轴旋转β角[1],如图1所示。
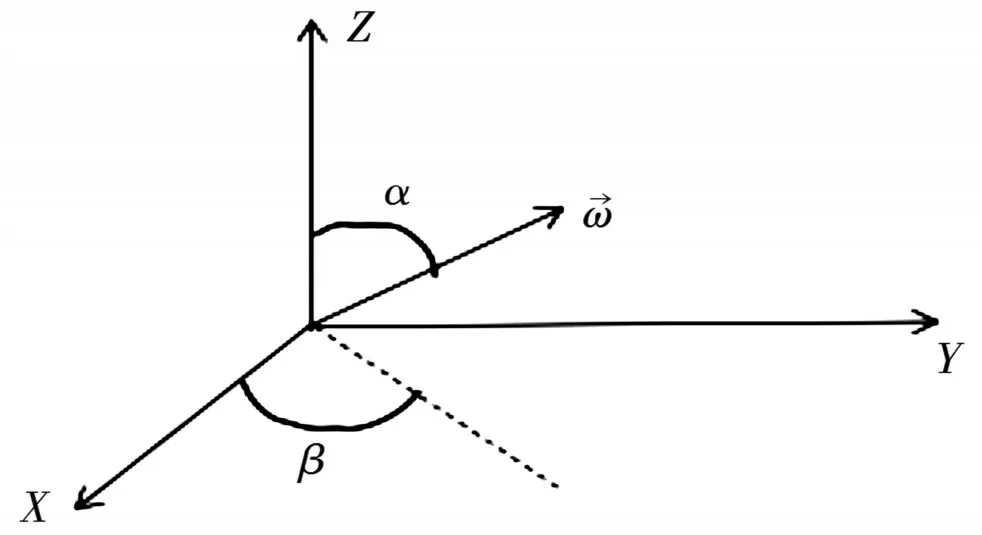
图1 轴角表示法
因为3次旋转都是绕固定轴旋转的,由基本旋转矩阵可得:

此矩阵可以分解为:

其中S(ω)是由ω生成的反对称矩阵。
该方程称为罗德里格斯旋转方程(Rodriguez rotation formula),只要知道旋转的旋转轴坐标和旋转角度,就可利用此方程求出旋转方程。例如,将刚体坐标系绕轴程为:

罗德里格斯方程还有如下3种不同的形式[2]:

其中第一种形式可以利用旋转矩阵的指数表示证明。
2 旋转矩阵的指数表示
假设刚体上一点P,它的位置向量为r,刚体绕方向为单位向量ω的轴以单位角速度旋转,则P 点在参考坐标系中的线速度为:

这是一个一阶线性微分方程,分离变量后,积分可得通解为:

其中r(0)是P 点的初始位置向量,eS(ω)t是一个矩阵的指数函数,由矩阵指数函数的定义有:

直接利用级数来计算旋转矩阵R( ω,θ )较麻烦,现利用矩阵论的知识来简化R( ω,θ )的计算。

其特征多项式为:

根据矩阵论中哈密尔顿-凯莱(Hamilton-Cayley)定理:若n 阶矩阵A的特征多项式为:

根据此结论可以只用S(ω)和( S(ω))2来表示旋转矩阵,即:

再由正弦函数和余弦函数的幂级数展开式得:

所以

根据前面的证明也可得:
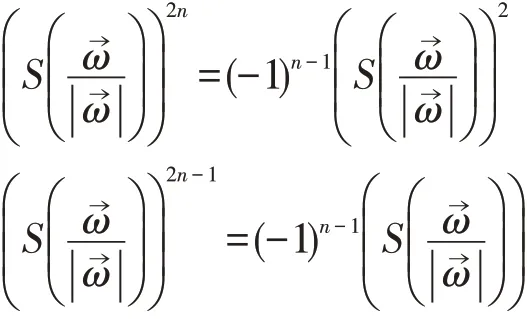
代入(3)式,整理得:

上式即为修正的罗德里格斯公式。罗德里格斯公式是一种非常有效的计算eS(ω)θ的公式。
由于两相似矩阵的的特征值相同,若矩阵A与对角矩阵Λ相似,则对角矩阵主对角线上的元素即为A的特征值。

且存在可逆矩阵P,使得:

但是并不是每一个矩阵都与对角矩阵相似,在复数域上n阶方阵与其若当(Jordan)标准型J相似,即存在可逆矩阵P使得
A = PJP-1
若当标准型J主对角线上的元素即为矩阵A的特征值,设
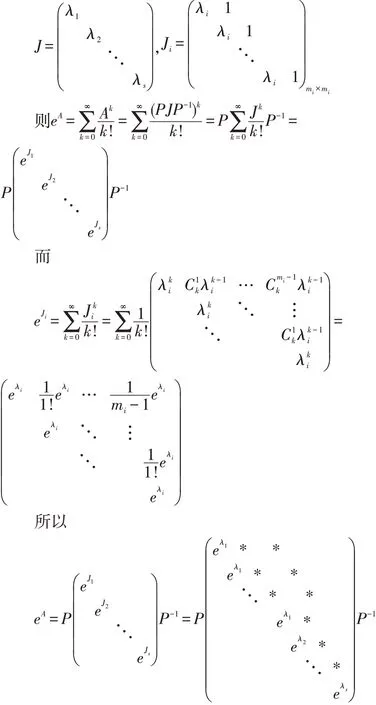
从上式可知eA与上三角矩阵
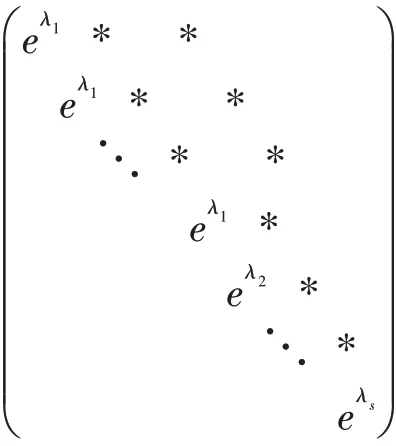
相似,可以证明上三角矩阵的特征值是其主对角线上的元素,故eA的特征值为eλ1,eλ2,…,eλs。
从而,eS(ω)θ的特征值为1,eiθ和e-iθ。根据特征的定义,对应于特征值1,有

因为在绕轴旋转时,轴保持不动,所以特征值1对应的特征向量就是kω(k ≠0).
3 螺旋运动与罗德里格斯公式
由查尔斯定理(Chasles theorem)知,刚体的任何位移可以看成由沿空间特定直线的平移和绕该直线的旋转生成的。这种平动和转动相结合的运动称为螺旋运动。
设旋转轴方向为ω,沿轴方向的平移为h,绕轴旋转的角度为θ,称平移h和旋转的角度θ的比值螺旋运动的步距[2]。利用单位向量ω,旋转轴上任意点的位置向量s 就可确定旋转轴在参考坐标系中的位置。再加上旋转角θ和步距p,就可以定义刚体坐标系相对于参考坐标系的位姿。
在轴角表示法表示旋转矩阵中,只有旋转,没有平移,所以h=0,而且这时轴通过参考坐标系原点,可得量是旋转后的位置向量,则:


这就是一般刚体运动的罗德里格斯公式。
从上边的证明和讨论,可以看到罗德里格斯公式在刚体旋转运动和一般运动中都有很重要的应用,利用它可以很容易计算旋转矩阵和运动后刚体上任意一点的位置向量。

