地震作用下筒仓结构贮料侧压力计算方法
周长东,张泳,邱意坤,梁立灿,阿斯哈
(北京交通大学 土木建筑工程学院,北京 100044)
在钢筋混凝土筒仓的抗震设计中,通常将筒仓当作悬臂结构来计算整个结构根部的内力,并采用截面强度设计,忽略了贮料侧压力对筒仓壁的影响.实际上,该侧压力变化将在仓壁的圆周方向上引起弯曲应力,这对于筒仓这类薄壁结构是不利的.
近年来国内外学者对于筒仓贮料侧压力进行了广泛的研究.施卫星等[1-2]对2 个1 ∶10 钢筋混凝土圆筒仓结构模型进行了振动台试验,研究了地震作用下筒仓的动力响应和破坏形式,根据试验结果提出了储煤对仓壁侧压力计算方法;Holler 等[3]对动态激发下的存储颗粒材料的筒仓进行了有限元数值模拟,并将采用该模型获得的数值模拟结果与在法国Saclay 的振动台试验结果进行了比较分析;张翀等[4-5]分析了各种卸料工况下仓壁应变的变化规律;赵松[6]进行了钢筒仓侧压力模型试验,得到了筒仓结构静止及卸料状态下的贮料侧压力分布曲线;周长东等[7]针对筒仓静力作用提出了一种散粒体的亚塑性本构模型,分析了贮料对仓壁的静止侧压力;庞照昆等[8]通过模型试验方法,研究了筒仓在侧壁卸料与中心卸料的动态超压现象.
目前的研究大多集中于静力状态以及卸料状态下贮料侧压力的变化[9-13],主要通过理论分析法、有限单元法以及离散元法进行分析,而少有对于地震作用下贮料侧压力分布的研究.考虑地震作用时,离散元法虽然可以较好地模拟颗粒之间的相互作用,但输入地震波的困难让该方法难以应用;有限元法数值计算的精度及稳定性高,但是由于其对特定结构进行数值分析,并不能得出一个普遍的贮料侧压力计算方法;理论分析法在地震作用下受多种因素的限制,并不能单独通过公式推导得出所需的计算参数[14].
本文首先对地震作用下考虑筒仓-贮料相互作用的贮料侧压力计算方法进行理论分析,确定贮料侧压力计算中所需要的修正参数;然后利用ABAQUS 建立筒仓结构数值模型进行计算,获取与影响参数相应的贮料侧压力变化曲线;随后对贮料侧压力变化曲线进行拟合,得到相应参数在贮料侧压力计算中的修正值;之后综合不同参数拟合结果,归纳出考虑筒仓-贮料相互作用的贮料侧压力修正公式;最后,将根据贮料侧压力修正公式所得的计算值与既有试验数据及规范设计值进行对比分析,验证计算公式的合理性.
1 地震作用下贮料侧压力计算
目前针对地震作用下贮料侧压力计算方法的研究中,仅有施卫星等通过试验与理论相结合的形式,推导出符合相应试验模型的地震作用下贮料侧压力计算方法[2].因此,本文结合数值模拟的方法,在“施卫星”计算方法的基础上进行修正,得到可在实际工程应用的地震作用下贮料侧压力计算方法.
1.1 “施卫星”计算方法
施卫星等[2]提出以计算筒仓贮料质心处的煤侧压力为主,再通过各种修正系数去计算贮料上层及底层的侧压力的计算方法.
当地震作用于筒仓时,在其贮料质心处的绝对加速度为Sa,对称压力Pce不可能使贮料产生加速度,而偏心压力Pee(θ)使贮料产生了Sa加速度,假设Pee(θ)的分布满足:

式中:Pe=Pmin+Pmax为地震作用下贮料侧压力变化值.
Pee(θ)在x 方向上的合力为
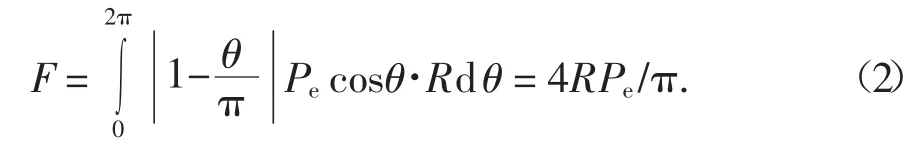
因为F=πR2γSa/g,所以Pe=π2RγSa/4g.
考虑到贮料质心加速度是贮料侧压力及贮料层间摩擦力共同作用的结果,因此使得计算所得侧压力与实际值有所差别,施卫星对该公式进行了修正:

式中:Ce由试验结果确定,与测点位置、台面加速度、贮料内摩擦角和湿度等因素有关.
为求解出工程设计时考虑的最大贮料侧压力Pmax,需先计算最小贮料侧压力Pmin:
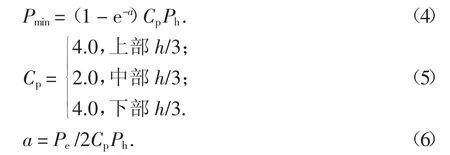
式中:h 为贮料高度;Cp为超压系数;Ph为Janssen 静压力.
综上,考虑筒仓-贮料相互作用的贮料侧压力计算方法需要确定6 个参数:筒仓半径、贮料质心处加速度、计算截面位置、贮料容重、内摩擦角、贮料与仓壁摩擦因数.
1.2 简化计算方法
应用公式(3)进行地震作用下贮料侧压力计算时,需要输入贮料质心处加速度.而工程设计时,无法直接得到贮料质心加速度,可通过综合考虑测点位置、贮料内摩擦角及摩擦因数等因素,对台面加速度进行相应修正后[2],得到:

式中:Cg为考虑地震强度的修正系数;Ch为考虑贮料高度的修正系数;Cφ为考虑贮料内摩擦角的修正系数;Cμ为考虑摩擦因数的修正系数.
在求解出地震作用下贮料侧压力变化值Pe后,需要确定地震作用下最小贮料侧压力Pmin来确定最大贮料侧压力Pmax.根据文献[15]中提供的筒仓在静力状态以及地震作用下的贮料侧压力数值模拟分析结果可看出,筒仓结构在地震作用下的最小贮料侧压力Pmin<静力状态下贮料侧压力,与施卫星定义下的Pmin计算公式相悖.在工程设计时通常将最大贮料侧压力Pmax作为主要设计影响因素,因此对地震作用下最大贮料侧压力Pmax进行简化计算,综合考虑式(3)与式(7)对最大贮料侧压力Pmax进行修正,即:
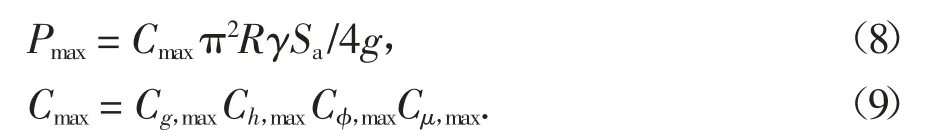
式中:Cg,max为考虑地震强度的最大贮料侧压力修正系数;Ch,max为考虑贮料高度的最大贮料侧压力修正系数;Cφ,max为考虑贮料内摩擦角的最大贮料侧压力修正系数;Cμ,max为考虑摩擦因数的最大贮料侧压力修正系数.
筒仓结构设计时,根据结构所在地区的环境参数和设定的材料参数,建立有限元分析模型,选取合理的地震波进行筒仓结构的地震响应分析,获取公式(9)中的修正系数,即可计算得到设计所需的最大贮料侧压力.
2 筒仓结构有限元分析模型
2.1 工程概况
以浙江某粮库的筒仓结构为工程背景,将钢筋混凝土筒仓群中的单一筒仓作为设计模拟的原型(如图1 所示).建筑物总高度35.0 m,粮食装载高度27.0 m,筒仓单仓内径12.0 m,筒仓壁厚0.22 m;环梁尺寸为0.4 m×0.8 m,门洞尺寸为1.8 m×2.7 m,窗洞尺寸为0.9 m×1.5 m.抗震设防烈度为7 度,设计地震组为第一组.抗震设防类别为乙类,框架抗震设防等级为二级,场地类别为Ⅲ类[16].
2.2 ABAQUS 有限元模型
采用ABAQUS 软件对所选取的单仓结构建立分析模型(见图1).选用混凝土损伤塑性本构模拟仓壁的混凝土材料(见表1),混凝土的单轴本构曲线采用《混凝土结构设计规范》(GB 50010—2010)附表C.2 中的推荐公式;选用理想弹塑性本构模拟钢筋(见表2);选用摩尔库伦本构模拟贮料(见表3).

图1 筒仓结构有限元模型Fig.1 Finite element model of silo structure
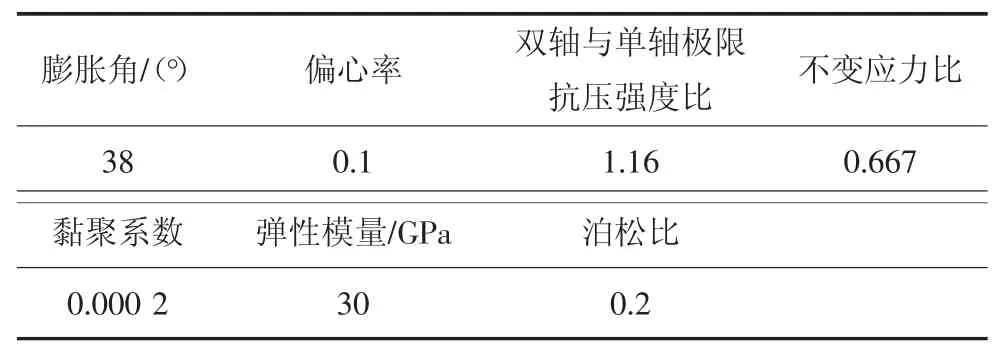
表1 混凝土损伤塑性本构参数取值Tab.1 Parameters of concrete damaged plasticity model

表2 钢筋理想弹塑性本构参数取值Tab.2 Parameters of elastic plastic model for steel bars

表3 贮料摩尔库伦本构参数取值Tab.3 Parameters of Mohr-Coulomb model
利用ABAQUS 中S4 单元模拟筒仓仓壁,利用C3D8R 单元模拟贮料;利用ABAQUS 自带的“接触对”来模拟仓壁与贮料的接触关系,其中选取仓壁内表面为主接触面,两者之间的摩擦因数为0.4.
2.3 模型验证
由模型试验[14]知,满仓状态下,在地震烈度为7度多遇和7 度基本时,上海人工波SHW2 对单仓y方向影响较大,因此在筒仓数值模型底部施加SHW2 波进行动力时程分析.为验证单仓模型的合理性,提取单仓模型y 方向单元最大加速度以及最大相对位移、自振频率值,与相应的筒仓结构模型试验结果进行对比,对比结果详见图2 和图3.

图2 数值模拟与振动台试验对比(位移)Fig.2 Comparison of experimental data and FEM results(displacement)

图3 数值模拟与振动台试验对比(加速度)Fig.3 Comparison of experimental data and FEM results(acceleration)
通过有限元模拟分析,得到满仓状态下数值模型的自振频率为2.617 Hz.振动台试验获取单仓一阶频率后,通过相似系数返回原型结构得到的原型结构自振频率为2.631 Hz.如图2 和图3 所示,将有限元模拟提取的最大加速度和最大相对位移值与单仓试验数据进行比较,偏差均在5%之内.因此,本文建立的单仓数值模型与振动台试验模型吻合较好,证明了数值模型的合理性.
3 最大贮料侧压力计算参数分析
采用增量动力分析(Incremental Dynamic Analysis,IDA)方法,针对不同地震波的峰值地面加速度(Peak Ground Acceleration,PGA)进行调幅并在数值模型底部输入,得到时程分析结果.为获取式(9)中的相应参数,需要拟合不同工况下贮料侧压力求解修正参数.在进行数值模拟计算时,单一模型输入的参数包括了地震动强度、贮料高度、内摩擦角以及摩擦因数,因此获得的贮料侧压力分布曲线不能直接通过拟合得到单一的修正参数.本文假定当PGA=0.1g、φ=28°、μ=0.40 条件下的筒仓贮料侧压力修正系数为1,即Cg=0.1,max=1、Cφ=28°,max=1、Cμ=0.4,max=1,在此条件下,通过变换不同参数进行数值模拟,将所得贮料侧压力分布曲线进行拟合.
3.1 地震波的选取
根据原型筒仓的工程概况,按《建筑抗震设计规范》[17]的要求选取两条天然波和一条人工波进行时程分析,分别选用El-Centro 波、NGA#178 号地震波以及上海人工地震波SHW2 波输入数值模型底部进行研究.图4 所示为所选地震波的平均反应谱,与建筑抗震设计规范中的设计反应谱吻合较好.
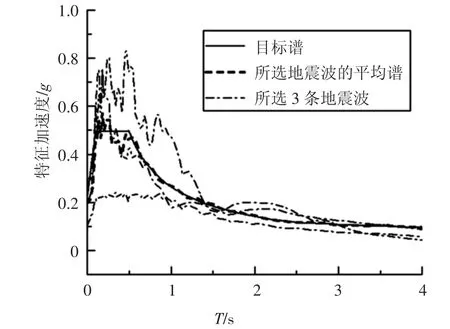
图4 所选地震反应谱Fig.4 Response spectra of the selected input ground motions
图5、图6、图7 分别为考虑地震动强度、内摩擦角以及摩擦因数影响下的最大贮料侧压力分布曲线,可发现贮料高度在不同参数中对最大贮料侧压力的影响最为明显.因此,首先考虑以PGA=0.1g 时筒仓最大贮料侧压力曲线为基准,对考虑贮料高度的最大贮料侧压力参数Ch,max进行拟合;随后对不同参数影响下最大贮料侧压力分布曲线进行拟合,确定不同参数影响下的最大贮料侧压力修正系数.
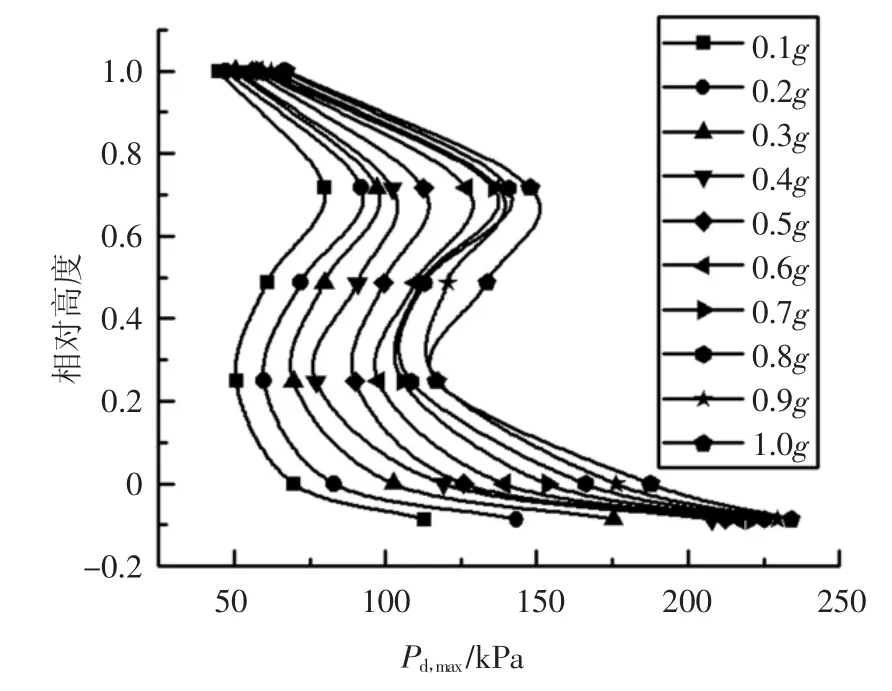
图5 不同地震强度的最大贮料侧压力分布曲线Fig.5 Maximum storage side pressure distributions of silo under different PGA
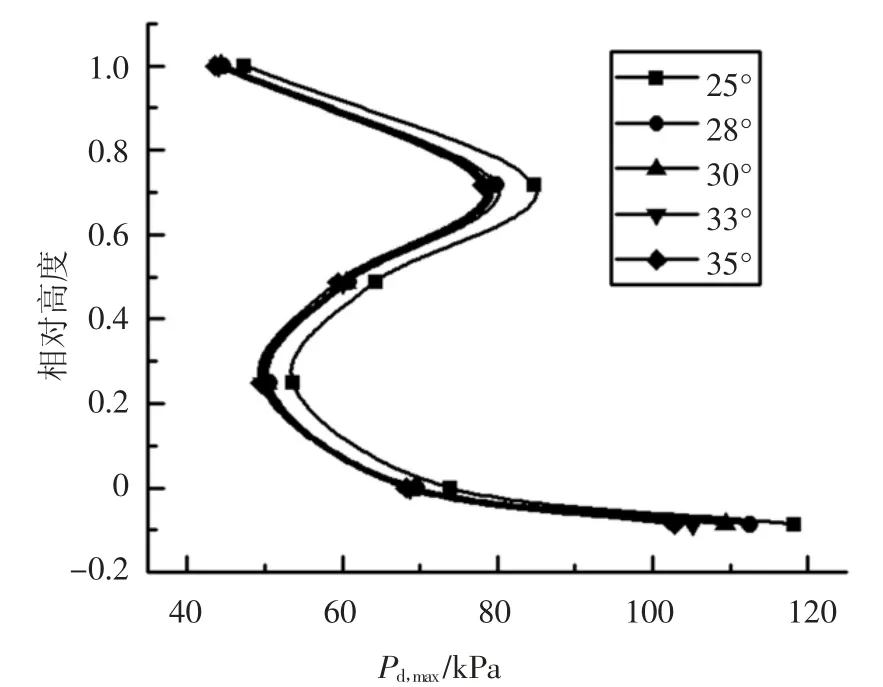
图6 不同内摩擦角的最大贮料侧压力分布曲线Fig.6 Maximum storage side pressure distributions of silo under different internal friction angles
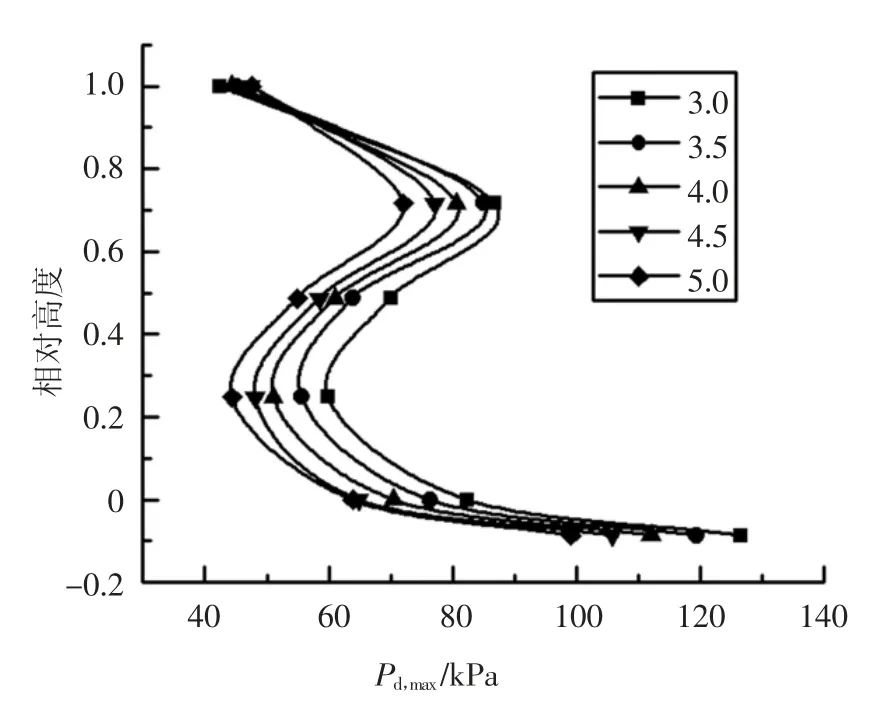
图7 不同摩擦因数的最大贮料侧压力分布曲线Fig.7 Maximum storage side pressure distributions of silo under different friction coefficients
3.2 考虑贮料高度的最大贮料侧压力参数
采用PGA=0.1g、贮料参数为φ=28°、μ=0.40的筒仓模型进行数值模拟计算,选用此参数可排除地震动强度、内摩擦角及贮料与仓壁的摩擦因数的影响.为求解考虑高度的最大贮料侧压力参数,将式(8)、式(9)进行变形,得:
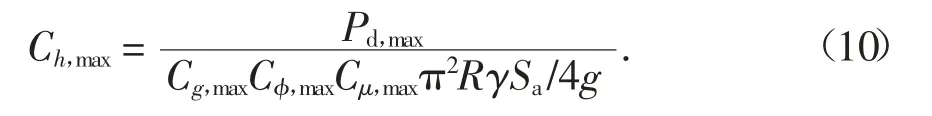
式中:Pd,max是仓壁受到的最大动压力.
图8 所示为筒仓结构在PGA=0.1g 地震作用下沿高度方向修正系数分布曲线.可以看出,筒仓沿高度方向的修正系数曲线可分为四段,分别为漏斗处、筒仓仓壁相对高度0~0.25、相对高度0.25~0.75、相对高度0.75~1.0.选取筒仓仓壁相对高度为0、0.25、0.5、0.75、1 处的修正系数进行分段拟合,如图9所示.

图8 PGA=0.1g 地震作用下的Ch,maxFig.8 Ch,max under 0.1g PGA
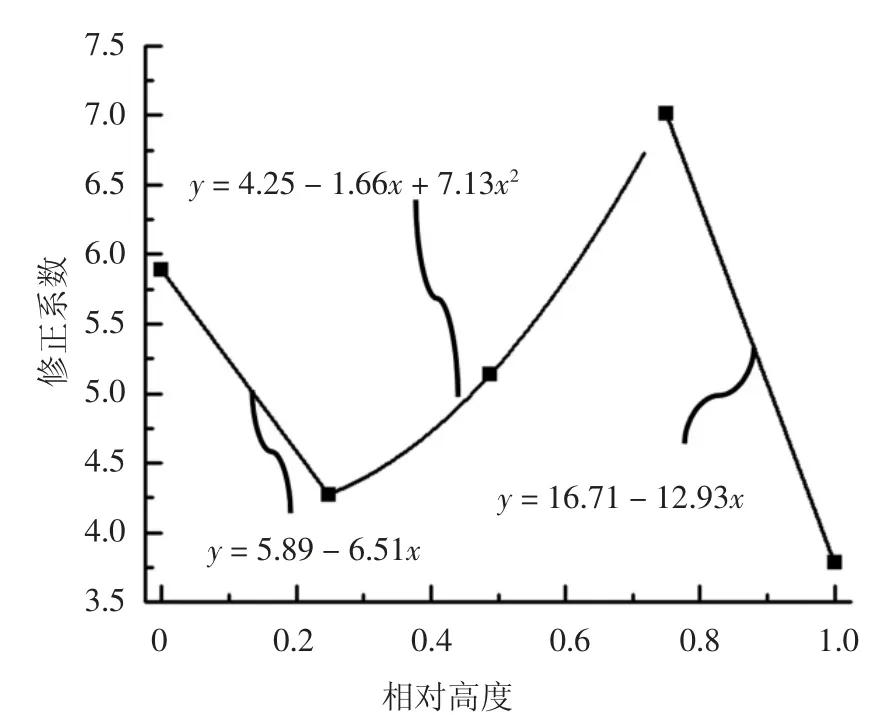
图9 考虑贮料高度的贮料侧压力修正系数拟合Fig.9 Fittings of storage side pressure’s correction coefficient considering storage height
根据图9 所示拟合结果,筒仓侧压力高度修正参数公式为:

3.3 考虑地震动强度的最大贮料侧压力参数
考虑贮料高度对筒仓侧压力计算的影响后,采用贮料参数为φ=28°、μ=0.40 的筒仓模型进行数值模拟计算,选用此参数可以排除内摩擦角、贮料与仓壁的摩擦因数的影响.为求解考虑地震动强度的最大贮料侧压力参数,将式(8)(9)进行变形,得:
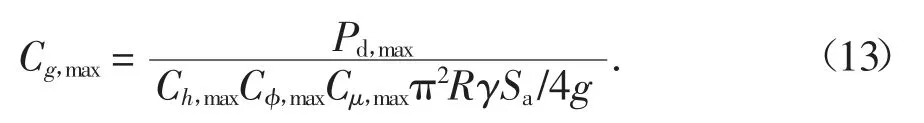
图10 所示是筒仓结构在不同地震动强度下的Cg,max分布曲线.由图10 可知,筒仓结构在不同高度处Cg,max的变化规律不同.图11 分别对位于筒仓漏斗处、筒仓仓壁相对高度为0、0.25、0.5、0.72、1 处不同地震动强度的Cg,max进行拟合,可以发现:在相对高度>0 的筒仓仓壁部位,PGA=0.1g~0.5g 时筒仓地震强度修正系数呈线性分布,PGA=0.6g~1.0g 时筒仓地震强度修正系数的分布形式为二次函数;在筒仓结构漏斗处,PGA=0.1g~0.4g 时筒仓结构地震强度修正系数呈线性分布,PGA=0.5g~1.0g 时修正系数分布形式为斜率不同的直线.因此,分段讨论分布函数公式.拟合分析后得出地震强度修正系数如下.

图10 地震作用下的Cg,maxFig.10 Cg,max under earthquake

图11 考虑地震动强度的贮料侧压力修正系数拟合Fig.11 Fittings of storage side pressure’s correction coefficient considering ground motion intensity
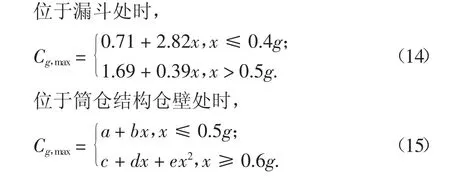
式中:a=0.80+0.14hm;b=2.12 -1.52hm;c=0.45;d=3.04;e=1.2.
3.4 考虑内摩擦角的最大贮料侧压力参数
为研究贮料之间的不同摩擦因数对贮料侧压力的影响,考虑选用φ=25°、28°、30°、33°、35°五种内摩擦角进行计算.本节采用贮料参数为PGA=0.1g、μ=0.40 的筒仓模型进行数值模拟计算,选用此参数可以排除地震动强度、贮料与仓壁的摩擦因数的影响.为求解考虑内摩擦角的最大贮料侧压力参数,将式(8)、式(9)进行变形,得:
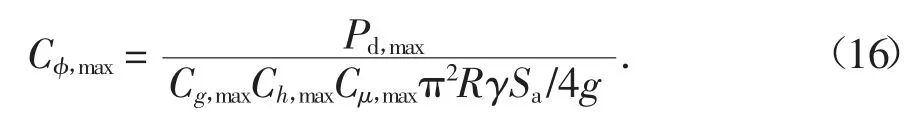
图12 是筒仓结构在PGA=0.1g 的地震作用下不同摩擦角修正系数分布曲线.由图12 可知,随着贮料内摩擦角的增大,考虑内摩擦角的最大贮料侧压力参数逐渐减小;当位于筒仓结构漏斗处时,随着内摩擦角的变化,考虑内摩擦角的最大贮料侧压力参数变化量基本相同;当位于筒仓结构中上部时,相同高度处随着内摩擦角的变化,考虑内摩擦角的最大贮料侧压力参数变化量有较大差异.因此,对该参数进行分段考虑,分别选取不同内摩擦角的漏斗处修正系数及筒仓仓壁相对高度为0、0.25、0.5、0.72、1处修正系数平均值进行拟合,如图13 所示.
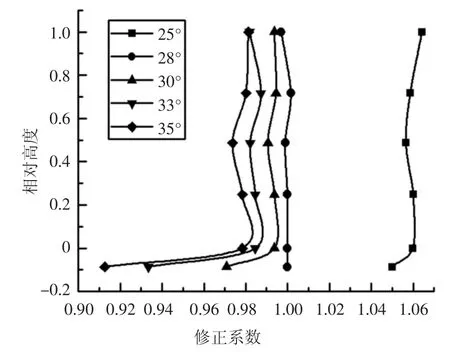
图12 PGA=0.1g 下不同内摩擦角的Cφ,maxFig.12 Cφ,max at different internal friction angles under 0.1g PGA
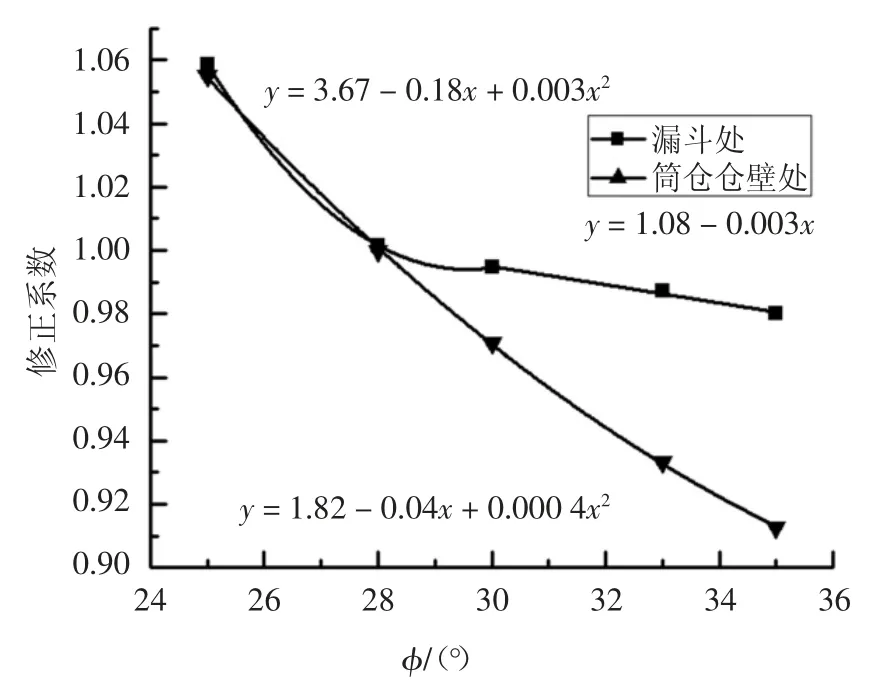
图13 考虑内摩擦角的贮料侧压力修正系数拟合Fig.13 Fittings of storage side pressure’s correction coefficient considering internal friction angle
图13 为漏斗处及筒仓仓壁处的Cφ,max拟合分析,考虑28°的内摩擦角修正系数为1,即修正系数公式如下.

3.5 考虑摩擦因数的最大贮料侧压力参数
为研究贮料与仓壁之间不同摩擦因数对贮料侧压力的影响,考虑采用μ=0.30、0.35、0.40、0.45、0.50五种摩擦因数进行计算.采用贮料参数为PGA=0.1 g、φ=28°的筒仓模型进行数值模拟计算,选用此参数可以排除地震动强度、贮料内摩擦角的影响.为求解考虑摩擦因数的最大贮料侧压力参数,将式(8)、式(9)进行变形,得:
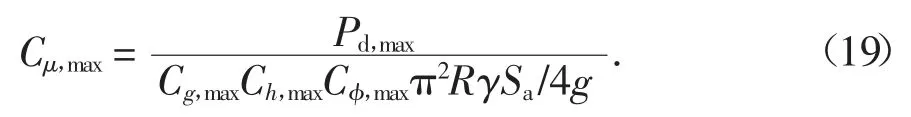
图14 所示是筒仓结构在PGA=0.1g 地震作用下不同摩擦因数的修正系数分布曲线.由图14 可知,随着筒仓仓壁与贮料摩擦因数的增大,Cμ,max逐渐减小;当位于筒仓结构漏斗处时,随着摩擦因数的变化,Cμ,max的变化量基本相同;当位于筒仓结构中下部时,摩擦因数引起的筒仓结构Cμ,max的变化量随着高度的增加基本不变;当位于筒仓结构上部时,摩擦因数引起的筒仓结构Cμ,max的变化量随着高度的增加而减小.因此,考虑将高度与摩擦因数的影响结合,进行分段考虑.

图14 PGA=0.1g 下不同摩擦因数的Cμ,maxFig.14 Cμ,max at with different friction coefficients under 0.1g PGA
图15 所示为漏斗处的Cμ,max的拟合分析,考虑摩擦因数为0.40 时的修正系数为1,即修正系数公式为:

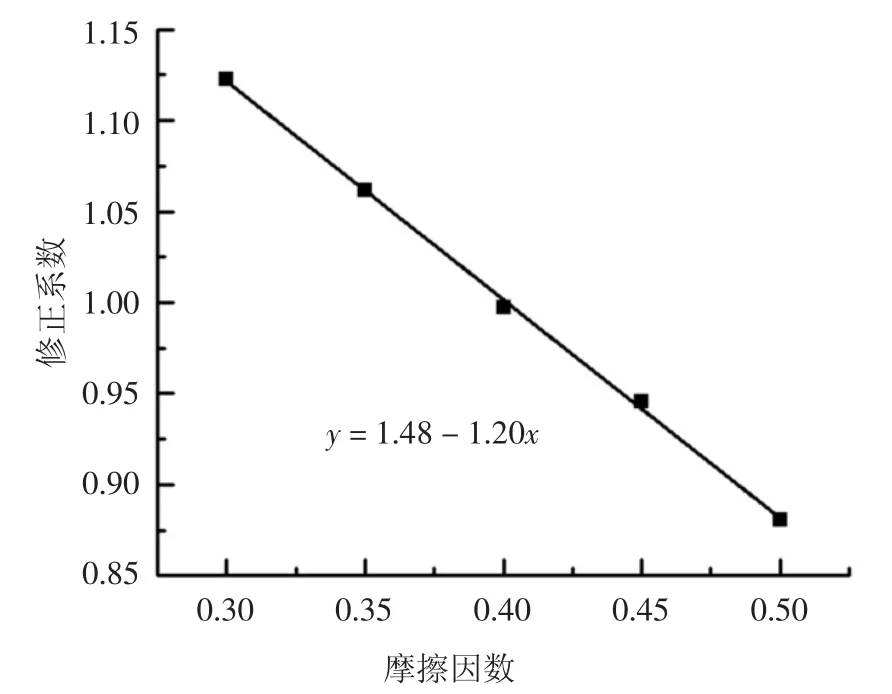
图15 漏斗处摩擦因数修正系数拟合Fig.15 Fittings of storage side pressure’s correction coefficient at funnel
图16(a)所示为筒仓中下部的Cμ,max的拟合分析,考虑摩擦因数为0.40 时的修正系数为1,即修正系数公式为:
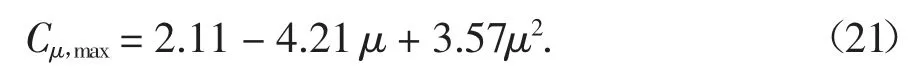
图16(b)、图16(c)所示为筒仓上部的Cμ,max拟合分析,考虑摩擦因数为0.40 时的修正系数为1,即修正系数公式为:

式中:a、b 为与相对高度hm有关的参数.

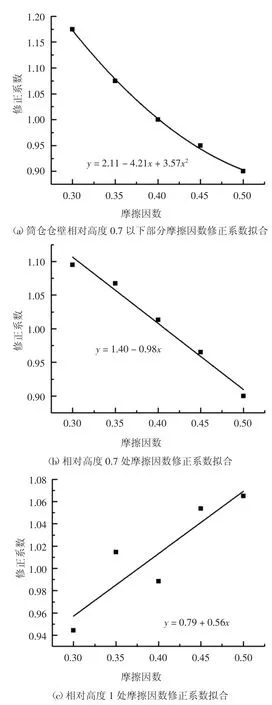
图16 仓壁贮料侧压力Cμ,max 拟合Fig.16 Fittings of storage side pressure’s correction coefficient at silo wall
4 计算值与试验数据对比
王录民等[18]通过模拟地震振动台试验对钢筋混凝土单仓及群仓模型进行研究,观察了贮料在地震作用下的侧压力变化规律.根据第3 节中得到的地震作用下修正的贮料侧压力计算公式,结合试验中的数据进行对比,对比分析结果如图17 所示.

图17 修正公式计算结果与试验数据对比曲线Fig.17 Comparison between calculated results of modified formula and test data
如图17 所示,7 度罕遇和8 度罕遇地震作用下,根据简化的最大贮料侧压力计算公式得到的模型结构贮料侧压力计算值与试验数据吻合较好;7 度基本地震作用下筒仓结构中部计算值与试验值有所差异,其原因在于模型试验时,在地震强度较小时,中部贮料由于散粒体的固结作用未能充分运动,因此试验值相对于计算值偏小;在7 度基本、7 度罕遇、8度罕遇地震作用下贮料底部及中上部计算值相对于试验数据稍微偏大,因此使用简化的最大贮料侧压力计算公式能合理反映实际地震作用下侧压力分布,保证了采用该公式设计时结构的安全性.
5 计算值与规范设计值对比
目前,比较经典的筒仓压力分布理论主要有Janssen 理论、Rankine 理论、Airy 理论以及修正的Coulomb 理论等.我国在进行深仓贮料压力计算[19]时,以Janssen 公式为理论基础,同时在设计时考虑相应的放大系数:
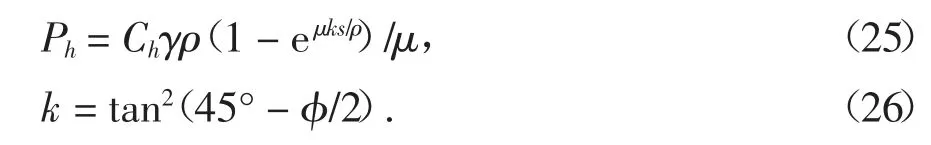
式中:Ph为高度h 处仓壁受到的法向侧压力;γ 为贮料的重力密度,kN/m3;μ 为筒仓仓壁与贮料的摩擦因数;ρ 为筒仓结构的水力半径,m;k 为主动侧压力系数;Ch为深仓贮料水平压力修正系数.
在考虑筒仓侧压力静力计算时,取Ch=1 进行计算;在进行筒仓结构设计时,需进行深仓贮料水平侧压力修正,见表4[19].
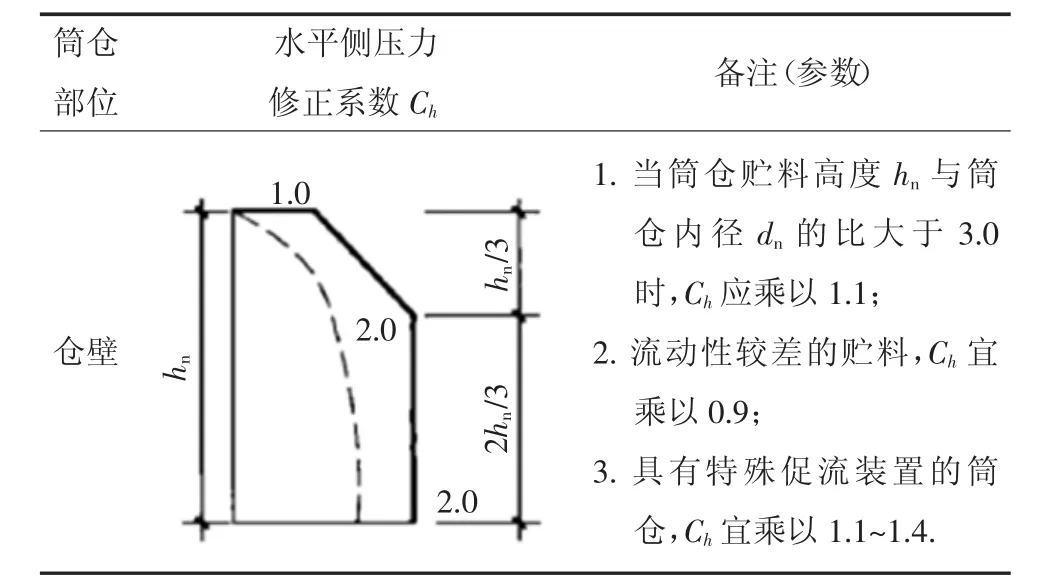
表4 深仓贮料水平侧压力修正系数Tab.4 Horizontal side pressure correction factor of deep storage
将经过第3 节相关系数修正后得到的地震作用下贮料侧压力简化计算公式所得的计算结果与我国规范对筒仓贮料压力设计值进行对比,如图18 所示.可以发现,贮料压力设计值随高度增大,侧压力逐渐减小.当高度h 小于1 m 时,贮料侧压力简化计算值随高度增大而减小;当1 m ≤h ≤1.5 m 时,计算值随高度增大而增大;当h >1.5 m 时,计算值随高度增大而减小.这是由于规范设计值是通过放大系数对静力作用下贮料侧压力进行修正;而地震作用下,由于筒仓结构中下部填充密实,贮料与筒仓仓壁相互作用较小;筒仓结构中上部贮料则由于填充密实度较差,因此动力作用下与筒仓仓壁相互作用较大,造成筒仓结构中上部出现贮料侧压力增大的情况.筒仓结构顶部则由于贮料较少,因此在h >1.5 m 时,侧压力随高度增大而减小.
如图18 所示,在7 度基本烈度地震作用下,筒仓结构中下部动态侧压力均小于规范设计值,可见在7 度抗震设防地区按照规范设计值对仓壁进行承载力计算偏于保守;而筒仓中上部动态侧压力计算值均大于规范设计值,按照规范设计筒仓中上部偏于危险;在7 度罕遇烈度及8 度罕遇烈度下,筒仓动态侧压力均大于规范设计值,可见在考虑强震作用下按照规范设计值偏于危险.因此采用本文修正的地震作用下贮料侧压力简化计算公式进行筒仓结构设计,能够保证筒仓结构抗震设计的安全性.

图18 修正公式计算结果与规范设计值对比曲线Fig.18 Comparison between calculated results of modified formula and design values
6 结论
本文首先对筒仓结构在地震作用下的贮料侧压力计算理论进行分析,在考虑工程实际后,对施卫星提出的计算方法进行了相关影响参数的修正研究,得到以下结论:
1)考虑贮料高度、地震动强度、贮料内摩擦角和贮料与仓壁之间的摩擦因数对贮料侧压力的影响,进行了相关系数的修正,给出了地震作用下贮料侧压力的简化计算公式.
2)根据本文提出的地震作用下贮料侧压力的简化公式计算得到的模型结构贮料侧压力与试验数据进行对比,计算值比试验数据稍微偏大,本文推荐公式能够真实合理地反映地震作用下贮料侧压力分布,并且也保证了根据该公式设计时的筒仓结构的安全性.
3)根据本文提出的地震作用下贮料侧压力的简化计算公式计算得到的模型结构动态侧压力与我国规范对筒仓贮料压力设计值进行对比,在7 度抗震设防地区按照规范设计时,筒仓下部偏于保守,中上部偏于危险;在考虑强震作用时按照规范设计筒仓结构均偏于危险.采用本文推荐公式计算地震作用下的贮料侧压力更能保证筒仓结构设计的安全.

