Q500GJ 高强度钢材焊接H 形柱抗震性能试验研究
李元齐,潘斯勇,李丽,朱晶
(1.同济大学 建筑工程系,上海 200092;2.南京钢铁集团有限公司,南京 210035)
相对于普通钢材,钢结构采用高强度钢材具有以下优点:能够减小构件尺寸和结构重量,减少各种涂层的用量和施工工作量;增加建筑物的使用净空间;能够减小板厚,从而减小焊缝厚度,改善焊缝质量,提高结构疲劳使用寿命;能够降低钢材用量,从而大大减少资源消耗.以上均能够创造良好的经济效益[1-2].
高强度钢材力学性能的变化,必然导致其结构构件承载性能的改变,但国内外钢结构设计规范均没有专门针对高强度钢材钢结构的设计方法和计算理论.我国2017 版钢结构设计标准涵盖的最高强度钢材仅为Q460 钢材,尚不涉及超高强度钢材钢结构.高强钢相较于普通钢屈服平台长度较短、屈强比较高,难以满足抗震规范要求[3],阻碍了高强钢在抗震结构中的应用[4].近年来国内外对高强钢的轴压性能试验做了较多的研究[5-6],但对高强钢的抗震性能的试验研究还很少.清华大学[7-8]做了Q460C 高强钢焊接箱形和工字形截面压弯构件水平往复加载试验研究,同济大学[9-18]进行了Q460、Q460C、Q690D 高强钢焊接截面低周反复加载试验研究及节点试验研究.目前国内外对Q500GJ 高强钢柱的抗震性能研究还较少.本文进行了5 个Q500GJ 高强钢焊接H形柱在常轴力、水平反复荷载下的试验,研究Q500GJ高强钢H 形柱在反复荷载作用下的性能,从承载力、变形和耗能等方面评估Q500GJ 高强钢柱的抗震性能.
1 试验设计
1.1 试件设计
根据南京钢铁集团公司提供的2 种钢板厚度(20 mm,32 mm),设计了2 种H 形钢截面,分别为H250×250×20×20,H300×300×20×32.H250×250×20×20 绕强轴反复推拉设计1 种长细比的试件,H300×300×20×32 绕强轴反复推拉设计2 种长细比的试件,绕弱轴反复推拉设计2 种长细比的试件.考虑到加工的方便以及试验装置的尺寸,试件的长度稍作调整,全部取整,见表1.
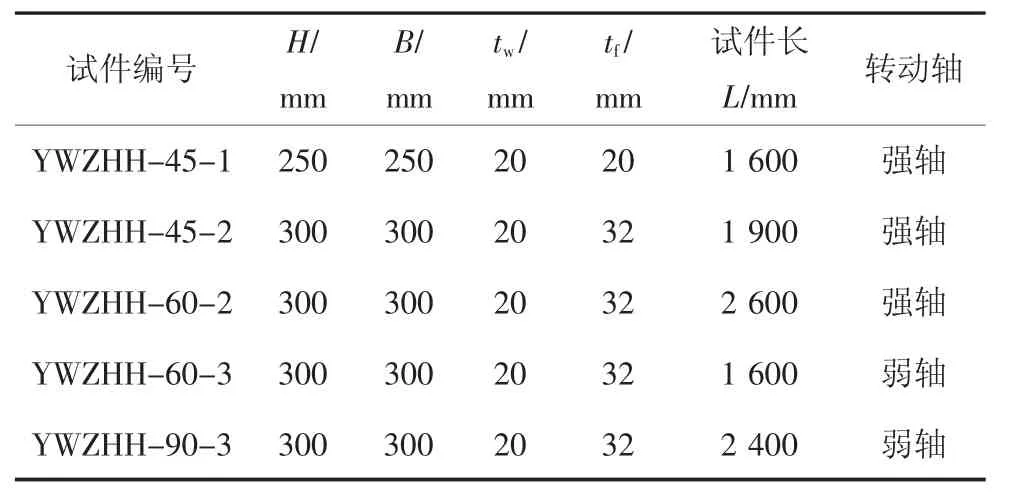
表1 截面参数Tab.1 Section parameters
试件设计时考虑钢结构设计规范对实腹受压构件不出现局部失稳的板件宽厚比要求,试件截面的宽厚比均满足要求.其中h、b、tw、tf、H、B 含义见图1.

图1 试件尺寸Fig.1 Specimen dimension
试件加工中加劲板均采用Q345B 材质.焊接H形钢本体焊缝、H 形钢与端板焊缝均采用坡口全熔透焊缝,并匹配南京钢铁集团公司推荐的Q500GJ 等强度的高强焊丝焊接而成.加劲板与H 形钢及端板的焊接均采用角焊缝焊接.
1.2 试验装置及支座设计
本试验采用同济大学建筑结构实验室10 000 kN 大型多功能结构试验机系统进行加载,如图2所示.
试验采用悬臂柱模型,柱底部端板采用高强螺栓与底座刚接,柱顶施加水平力和竖向轴力,柱顶采用销轴连接(如图3 所示),销轴可自由转动,释放弯矩,满足荷载施加条件.

图2 大型结构试验机系统Fig.2 Large-scale structural experiment system

图3 试件加工图Fig.3 Factory drawing for specimens
1.3 加载方案
试件安装时将上下支座调平对中,并使试件的上下端板投影重合.试件安装完毕后先实施预加载,检查应变仪、位移计等监测设备的运行状况,判定位移计方向.初始偏心在加载前已测量完毕,预加载阶段不再进行物理对中,只判断截面应力应变情况是否与初始缺陷情况相符合.各项准备工作检查无误后进行正式加载.
本试验正式加载时先以荷载控制在柱顶部一次施加轴力到预定值,轴压比统一取0.4,后保持不变,将所有螺栓全部拧紧;以位移控制施加反复水平荷载.加载制度按照规范ATC-24 中选用,如图4 所示.此处Δy是试件最外边缘开始屈服时的柱顶侧向位移.在屈服位移范围内,每级循环2 圈;超过屈服位移加载,每级循环3 圈.
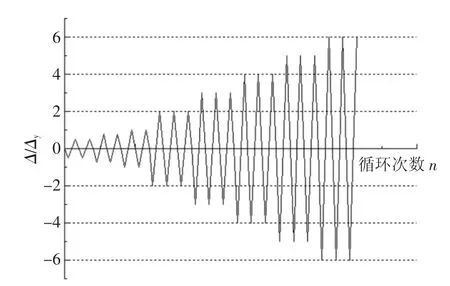
图4 压弯试件水平位移加载制度Fig.4 Horizontal displacement loading mechanism of compression bending specimens
1.4 材料性能试验
朱晶[19]根据《金属材料 拉伸试验 第1 部分:室温试验方法》(GB/T 228.1—2010)[20]对该Q500GJ高强钢材20 mm 及32 mm 板进行了材料性能试验,结合南京钢铁集团公司提供的相应板材的材料性能试验数据,得到材料屈服强度fy、抗拉强度fu、屈强比fy/fu、断后伸长率δ5等结果,见表2.

表2 Q500GJ 钢板静力拉伸力学性能参数(综合)Tab.2 Mechanical properties of Q500GJ steel plate
2 试验现象
试验中试件破坏前后形态如图5 所示.试件YWZHH-45-1 加载到3Δy时,翼缘出现轻微外鼓.翼缘局部屈服,构件耗能开始明显,滞回环面积加大.加载到5Δy时,北侧底部翼缘外鼓严重,南侧加劲肋往上0~500 mm 范围内,翼缘呈蛇形鼓曲,平面外呈S 形.试件端部形成塑性铰,水平承载力及刚度降低明显,试件耗能能力达到最大,滞回曲线饱满,停止加载.
试件YWZHH-45-2 加载到6Δy时,北侧底部翼缘外鼓严重,加劲肋往上0~500 mm 范围内,翼缘呈蛇形鼓曲,平面外呈S 形.试件端部形成塑性铰,水平承载力及刚度降低明显,试件耗能能力达到最大,滞回曲线饱满,停止加载.
试件YWZHH-60-2 加载到4Δy时,南侧底部0~250 mm 范围翼缘外鼓严重,试件向南倾,平面外呈反S 形.局部屈曲严重,水平承载力及刚度降低,滞回曲线饱满,停止加载.

图5 试件破坏前后比较Fig.5 Comparison before and after failure of specimens
试件YWZHH-90-3 加载到6Δy时,除强度及刚度降低明显外,未出现明显屈曲,试件全截面屈服形成塑性铰.滞回曲线饱满,停止加载.
3 试验结果分析
3.1 滞回性能
根据试验数据,可得出H 形截面柱的水平荷载和位移滞回曲线(H-Δ),如图6 所示.
随着位移幅值增大,试件YWZHH-45-1、YWZHH-45-2、YWZHH-60-2 底部翼缘均先出现局部屈曲.该试件均为绕截面强轴滞回加载,随着塑性变形的充分发展,柱底形成塑性铰,试件失去承载能力,试件破坏表现为板件的局部弹塑性失稳破坏,而试件YWZHH-60-3、YWZHH-90-3 均未出现明显局部屈曲,该试件均为绕截面弱轴滞回加载,试件材料进入塑性后,塑性充分发展至全截面塑性破坏,滞回曲线相对更为饱满.材料的高强度得到充分的发挥.5 个试件滞回曲线基本对称,各试件曲线较饱满,滞回性能较好.

图6 试件滞回曲线Fig.6 Hysteretic curves of specimens
3.2 骨架曲线
图7 给出了所有试件的水平荷载-侧移骨架曲线.所有骨架曲线正、反向基本对称,走势相似,从弹性变形到屈服点,达最大荷载后,开始下降直至塑性破坏.对同一长细比,如图8(a)所示,截面越大,试件的刚度越大,峰值荷载越大.
对同一种截面,同时绕强轴(见图8(b))或同时绕弱轴(见图8(c))加载时,长细比越小,试件的峰值荷载越大,侧移越小,峰值过后刚度退化越快.
对同一种截面,同一长细比,见图8(d),绕弱轴刚度大于绕强轴刚度.
3.3 位移延性系数及位移角
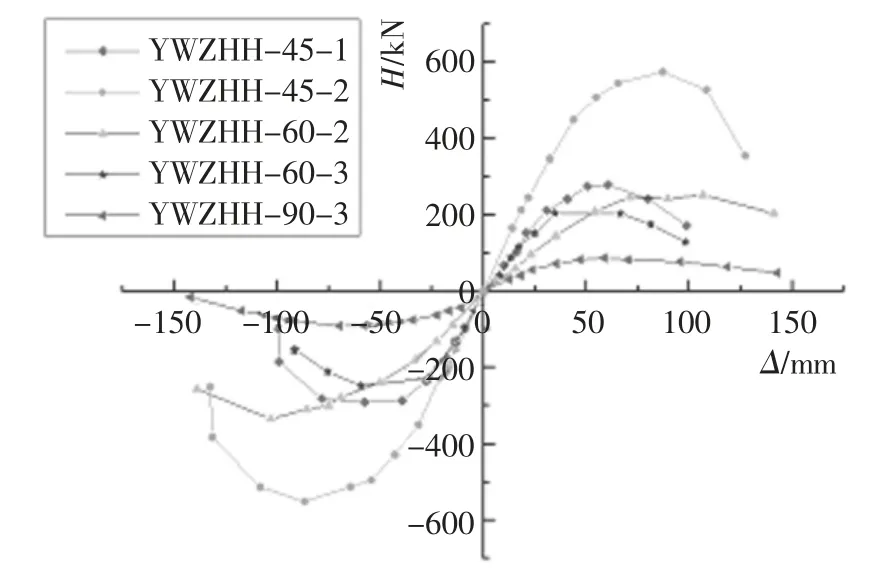
图7 试件荷载-位移骨架曲线Fig.7 Lateral load vs.displacement curves

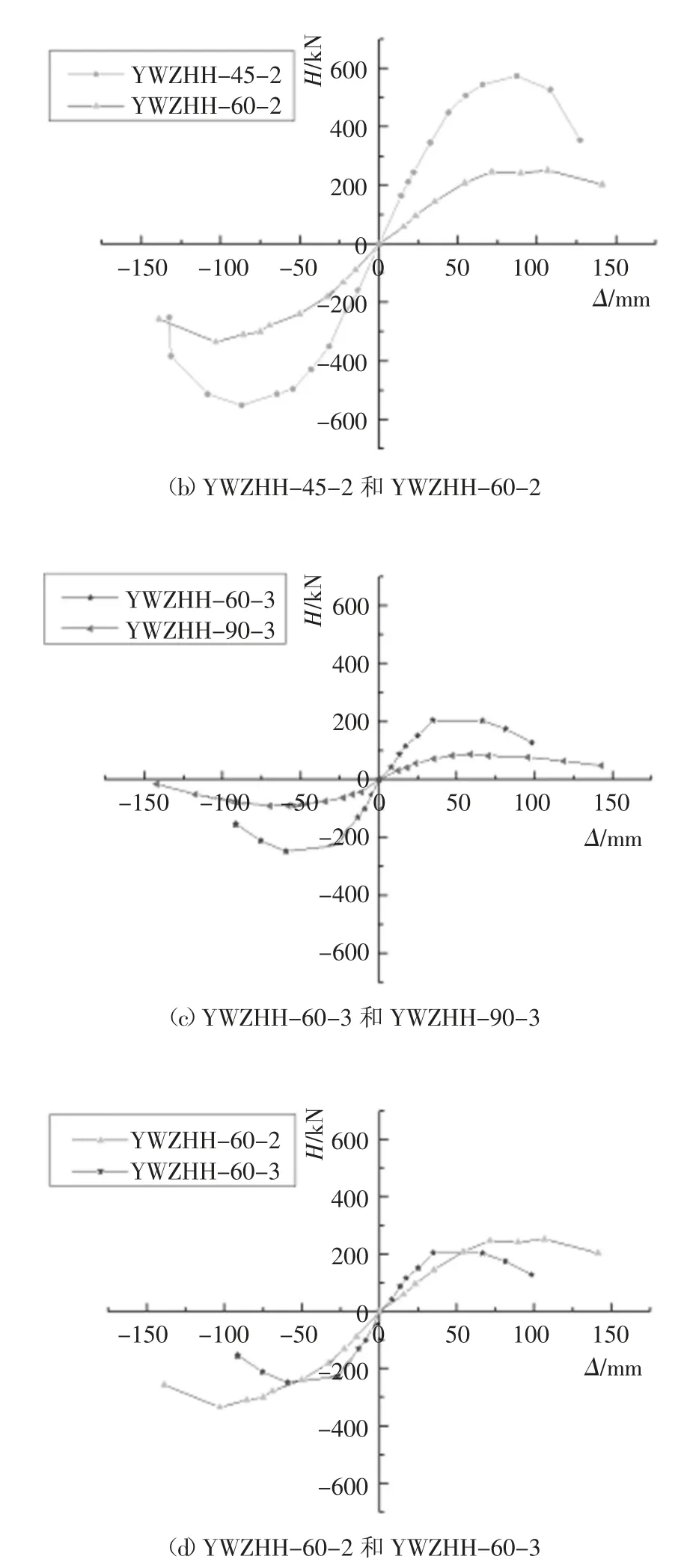
图8 骨架曲线对比Fig.8 Lateral load vs.displacement curves comparison
延性是衡量材料、构件或结构变形能力的重要参数,是指构件(材料或结构)破坏之前,在承载力无明显降低的条件下,经受塑性变形的能力.本文采用位移延性系数m 表达构件的延性,计算公式为:m=Δu/Δy.式中,Δu为构件的极限位移,取骨架曲线峰值荷载下降15%时对应的位移,对应的极限荷载为Hu;Δy为构件的屈服位移,采用等能量法[21]由骨架曲线计算得到,对应的屈服荷载为Hy;Δm为骨架曲线峰值荷载时对应的位移,峰值荷载为Hmax;等能量法的原理如图9 所示,计算原则如下:通过坐标原点O点作H-Δ 曲线的切线,过最高水平荷载点作一斜线相交于A 点,使得OAB 阴影面积与BCB 阴影面积相等,则A 点所对应的横、纵坐标即为屈服位移Δy和屈服荷载Vy.
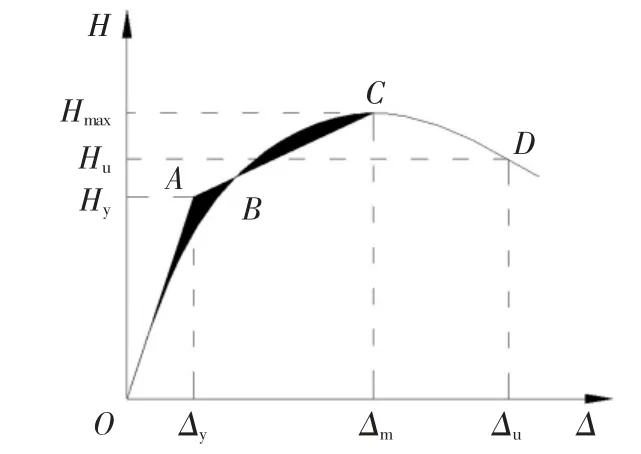
图9 等能量法Fig.9 The equal energy method
根据以上计算方法,表3 给出了各试件的延性系数.从表中延性数据可看出,试件绕弱轴反复荷载下延性系数要高于绕强轴反复荷载下的延性系数.这也与前面试件反复荷载下的破坏模式对应起来.试件YWZHH-45-1、YWZHH-45-2、YWZHH-60-2绕截面强轴滞回加载,表现为板件的局部弹塑性失稳破坏,截面的塑性发展不充分;而试件YWZHH-60-3、YWZHH-90-3 绕截面弱轴滞回加载,均未出现局部屈曲,试件全截面进入塑性后,塑性充分发展至破坏.

表3 试件延性系数及位移角计算Tab.3 Calculation of ductility coefficient and inter-story drift ratio of specimens
按照《建筑抗震设计规范》(GB 50011—2010)对多、高层钢结构层间位移角的限值要求,试件最大层间位移角θu=Δu/L,计算结果见表3.其中计算长度L 按照销轴中心至柱脚底部加劲肋上部位置计算.总体来看,5 根构件塑性发展和延性发展充分,具有很好的抗震性能,层间位移角均满足《建筑抗震设计规范》中对多、高层钢结构弹塑性层间位移角大于1/50 的限值要求.其中构件最大层间位移角为5.1%.
3.4 耗能能力
根据《建筑抗震试验方法规程》(JGJ 101—1996)[22]计算试件的能量耗散系数E,其随加载过程的变化如图10 所示.可以看出,对于同一个试件,随着水平位移加载幅值的增大,其塑性变形量增大,因此能量耗散系数不断增大.

图10 各试件能量耗散系数E 与循环次数曲线Fig.10 Energy dissipation coefficient vs.load cycle number curve
图11 给出了以水平位移Δ 为横坐标的各试件能量耗散系数.相同位移下,试件YWZHH-90-3、YWZHH-60-3 明显比试件YWZHH-45-2、YWZHH-60-2 耗能能力强,这也印证了前面绕弱轴滞回比绕强轴滞回延性好的结论.试件YWZHH-90-3 与试件YWZHH-60-3 的耗能能力以及试件YWZHH-45-2 与试件YWZHH-60-2 的耗能能力规律不明显,限于本文样本数量较少,不能说明长细比对试件耗能能力影响的规律.

图11 能量耗散系数与水平位移曲线Fig.11 Energy dissipation coefficient vs.horizontal displacement curve
3.5 不同等级高强钢构件位移延性对比
本文列举了其他学者关于高强钢抗震性能试验数据,见表4.本文H 形截面延性系数平均值为3.38,周峰等[14]的H 形截面延性系数平均值为3.8,陈素文等[12]的H 形截面、箱形截面延性系数平均值分别为3.32、2.84,施刚等[8]的箱形截面延性系数平均值为2.35.可以看出,相较于箱形截面,H 形截面的延性更好.各试验是在不同轴压比、不同长细比下的结果,总体来看,并没有出现强度等级越高,构件的延性系数越低的结论.Q500GJ 试验轴压比为0.4,轴压比越高,二阶效应的影响越大,Q500GJ 试件的延性系数及位移角结果处于中上水平,表明Q500GJ 有较好的抗震性能.
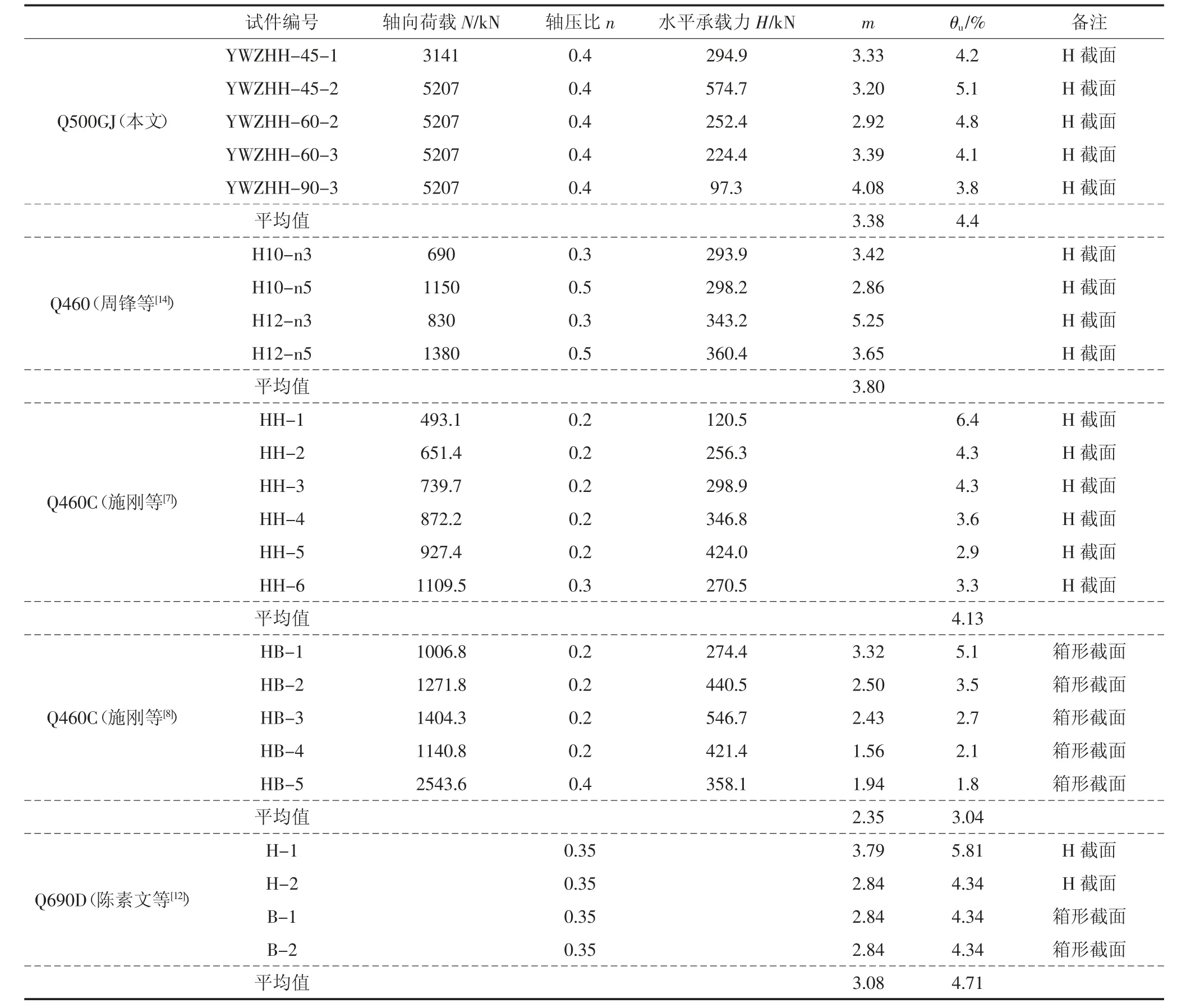
表4 不同等级高强钢延性对比Tab.4 Ductility comparison among different grade high strength steels
4 结论
对5 个Q500GJ 焊接H 形钢试件进行了低周反复荷载试验研究,主要结论如下:
1)3 个绕强轴滞回的试件均出现了底部板件局部屈曲,随着位移幅值增大,形成塑形铰直至破坏.2个绕弱轴滞回的试件均未出现明显的局部屈曲,随着位移幅值增大,全截面进入塑性形成塑形铰直至破坏.材料的高强度得到充分的发挥.绕弱轴荷载的试件截面的塑性发展比绕强轴荷载更充分.
2)所有试件荷载-位移滞回曲线饱满,滞回性能良好.骨架曲线正、反向基本对称,走势相似.试件具有良好的变形能力、耗能能力及抗震性能.
3)试件绕弱轴反复荷载下延性系数要高于绕强轴反复荷载下的延性系数.试件最大层间位移角为1/20,最小层间位移角为1/26,均满足《建筑抗震设计规范》(GB 50011—2010)中多、高层钢结构弹塑性位移角1/50 的限值要求.

