基于AnyLogic的我校校园行人流研究

程冉冉，张生晖

(华北科技学院 理学院, 北京 东燕郊 065201)

0 引言

众所周知，行人密度的大小、周围环境复杂程度以及安全性设计等方面的限制极大地阻碍了行人的紧急疏散。由于对高峰时段行人流数据的估计不足，导致设计者在道路设计中存在一些不安全因素，以致在紧急情况下，行人无法得到有效的逃离与避险，因此经常会产生严重的人员伤亡和重大的经济损失事件。

近年来，人们已经开始关注校园道路安全问题。随着社会教育程度的提高，高等教育的普及，源源不断的大学生来到大学校园学习生活，给校园道路交通带来了一定的压力。对此，为我校校园道路设计提供数据支持和优化，减少道路安全风险及安全隐患，是非常必要的。

目前对于道路等的优化问题，常用AnyLogic软件[1]进行模拟，它是一个专门用来模拟现实环境 ，设计行人交通灯等行为的复杂系统。现已有众多学者运用此软件进行行人流的研究[2-17]。

孙宇[3]对基于AnyLogic的地铁站优化方案进行了研究，考虑了乘地铁站的实际情况，并从改造工程的角度中提出三种可优化方案。文献[4]用AnyLogic模拟山坡社区泥石流灾害疏散，面对自然灾害和救灾运动后的内容，考虑到安全性和及时性，建立合理的疏散方案。刘栋栋[5]等研究了北京南站的行人特征参数，分析了关于疏散行人的相关影响因素；梁宪莹[6]对交通量特性及其道路规划设计进行了相关研究，阐述了交通量的含义与表达方式，探讨了交通量在时间和空间上的不均匀特性以及对交通的观测、换算方法和预测方法，总结了交通量的类型以及在道路规划和设计阶段的作用，并对拟建快速路进行实例分析；田郝青[7]等通过AnyLogic软件对地铁车站复杂场景行人流仿真进行了研究。

本文通过调查学生课后运动行为的集散情况得到所需数据，建立学生流模型，运用MATLAB进行可视化拟合。然后用AnyLogic软件中的行人库建立学生流微观仿真模型，分析学生的动态流向，观测并获取学校周围建筑物体的数据，得到热力图，进而分析人流拥堵情况，最后对学校道路优化及建设给出建议。

1 基本理论

在实际生活中，大部分学生课后选择先去食堂吃饭，然后回宿舍。考虑到教学楼、食堂、建筑物设计等因素，我们选择以1号楼(博观楼)和2号楼(致远楼)为研究对象。

1.1 校园行人调查地点及调查时间

为了收集到具有代表性的数据，我们选择了1号楼和2号楼。调查时间：由于下课时间是11：40，我们选择在11:35至11:50调查。具体操作如下：从出口向外扩张7米，形成矩形区域。我们用 N来代表矩形区域的人数，S代表矩形面积，v代表学生平均运动速度，σ代表学生密度，单个学生走出设置区域的时间为t，

(1)

σ=N/S

(2)

通过式(1)与式(2)得到学生的基本数值，整理后对1号楼和2号楼的调查中，共获得处理样本7493条，其中20条由于下课后学生来回穿插未能收集全，经剔除后剩余7473条可用样本数据。

1.2 学生流模型的建立与拟合

我们以交通行人流模型为基础，把每个学生想象为一辆行走的汽车。学生运动时的模型主要由密度、流量、速度三个参数因素构成，这三个因素相互影响、相互制约、相互联系。相同条件的车辆，流量、密度、速度模型具有一致性。在这些相互关系中，最重要的是速度-密度模型，其中格林希尔治模型和对数模型应用更加广泛。

1.2.1 格林希尔治(Greenshields)模型

1935年，格林希尔治(Greenshields)通过实测数据的分析提出了第一个速度—密度模型。虽然该模型在最初研究时所使用的数据存在一些问题，但格林希尔治速度—流量抛物线模型还是具有开创性意义的。他提出的速度—流量抛物线关系基本上反映了这两个参数的变化趋势，多年来一直被广泛使用。此外，该模型还提出一种重要思想，即只要确立了速度—密度关系模型，速度—流量、流量—密度关系模型也可相应确定。模型如下：

(3)

式中，uf为自由流车速；kj为阻塞密度。

在对应的学生流模型中，格林希尔治模型如式(4)，线性估计模型如图1。

u=b0+b1p

(4)

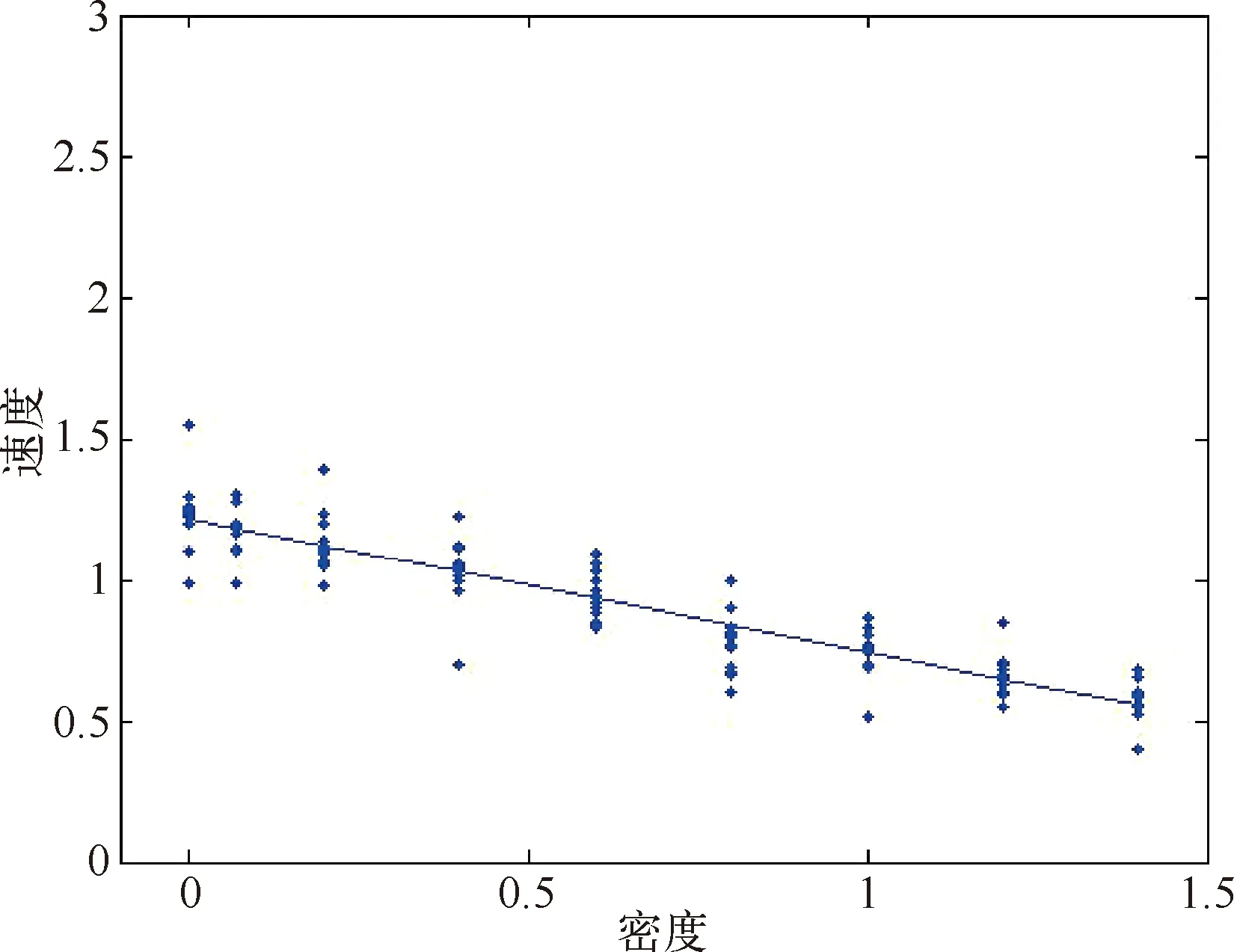
图1 格林希尔治线性模型

曲线估计结果为b0=1.2155，b1=-0.4729；即得到学生步行速度与学生密度p模型如下式：

u=-0.4729p+1.2155

1.2.2 格林伯(Greenberg)对数模型

(5)

式中，um为对应交通最大量的速度，最佳速度。模型如图2.

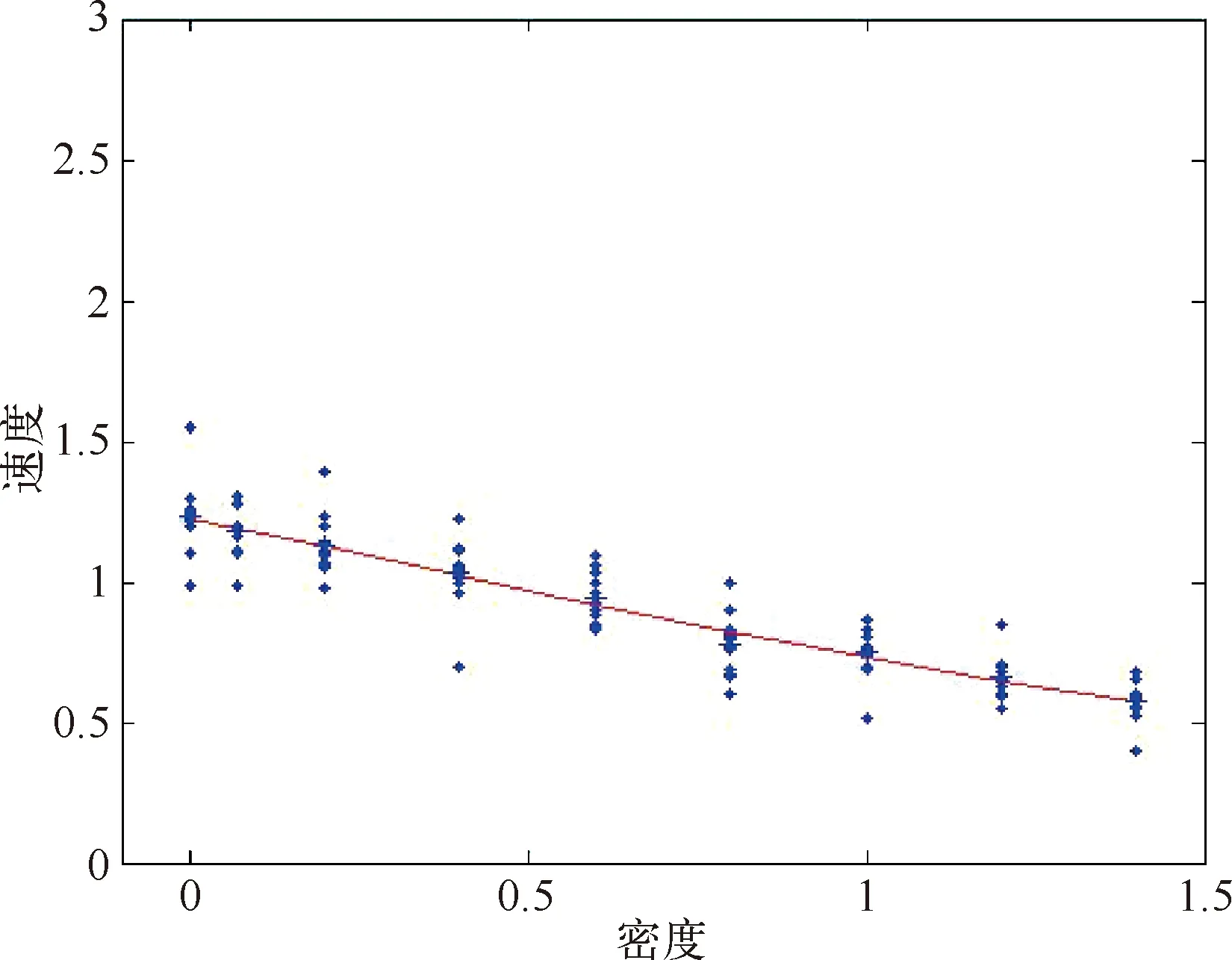
图2 Greenberg对数模型

当交通密度较大时，可使用此模型，但当密度较小时，此模型误差较大。我们校园学生流中，课后学生行走密度相对较小，所以我们得到的拟合效果不佳。

2 AnyLogic行人仿真

AnyLogic是一个专业虚拟原型环境，用于设计包括离散、连续和混合行为的复杂系统。AnyLogic可以帮助我们快速地构建被设计系统的仿真模型(虚拟原型)和系统的外围环境，包括物理设备和操作人员。软件中的行人是按照社会力模型移动，他会分析当前环境，选择一条最短路径，还可以避免与其他物体相撞，并进一步决定运动。

2.1 AnyLogic行人库模型建立

在利用AnyLogic创建相应的微观仿真模型之前需要分析学生下课后的流向，以及我们学校的建筑物几何参数，分析学生在下课后应该会选择的道路以及需要绕开的建筑。在获得建筑物及道路的几何数据后，将AnyLogic模型中的相应目标线长度按比例设置数值，设置目标线产生智能体的速率，智能体自动选择道路的方式，概率，初始速度，舒适速度，以及智能体的随机分布方式等。设置完成之后，将目标线与学生选择，学生分布流程连接，如图3所示。

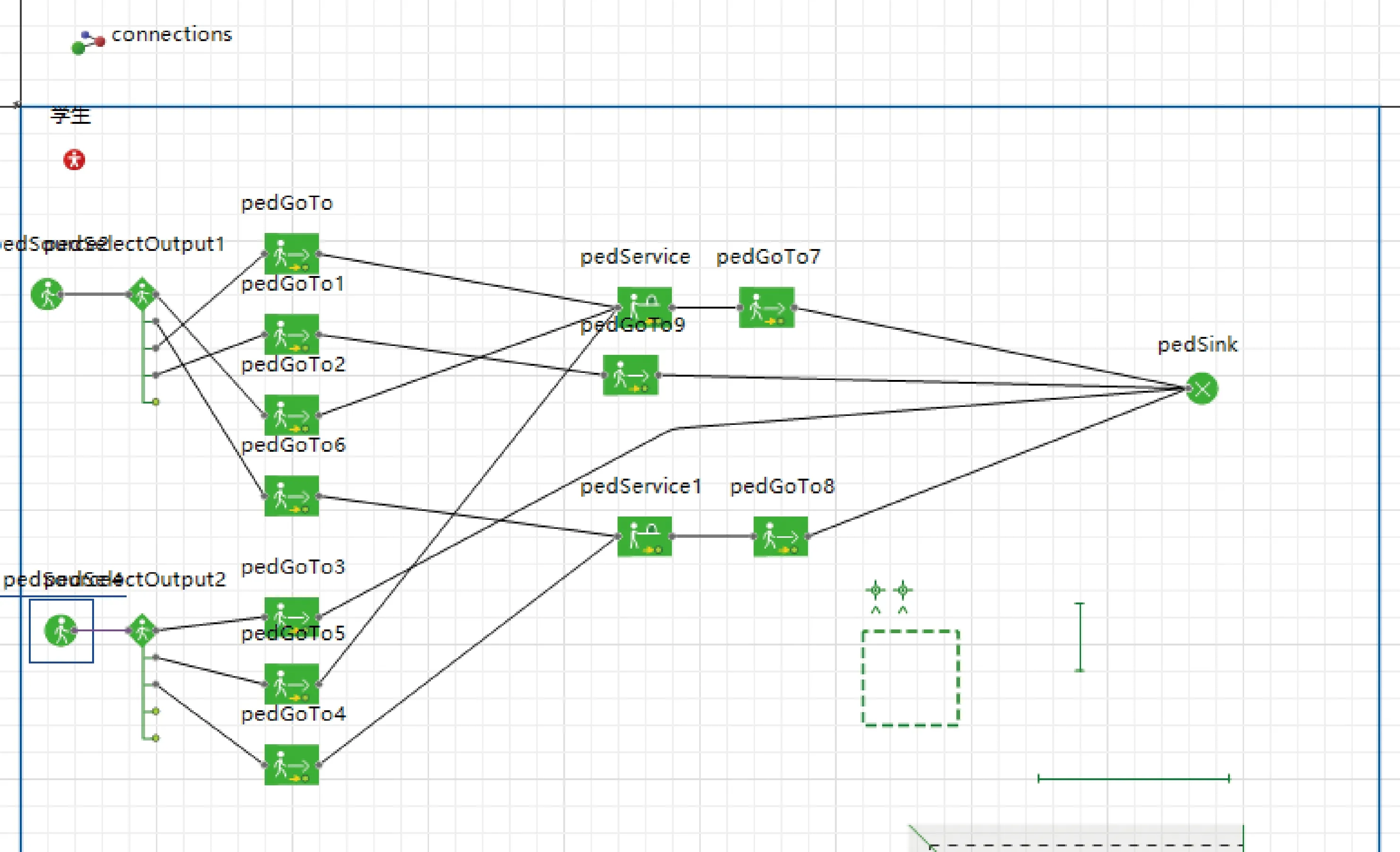
图3 AnyLogic行人库

在校园生活中，学生通常过着三点一线的生活，在教室-食堂-宿舍之间来回穿梭。实际上，还伴随着一些其他的行为如出校门、坐车等。通过分析，校园学生课后的主要行走路线如下图4所示。

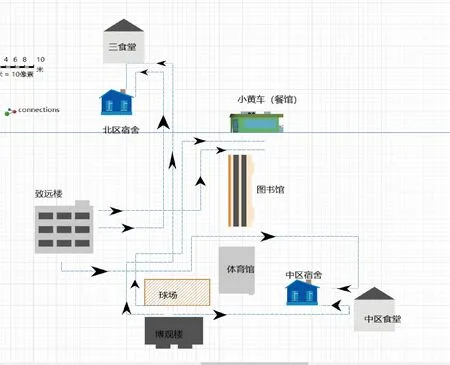
图4 学生行走主要路线图

2.2 仿真结果分析

由于下课铃响后，学生从教学楼出来需要一定的时间，故我们将录制时间定为下课前5分钟，即11:35开始，结束时间11:55。这样可以确保教学楼内的大部分学生都已经出来，并且路过我们所设定的地点，提高数据的准确度。经过调查统计得到的数据为学生走出教学楼的累计数量-时间关系如图5和图6所示。

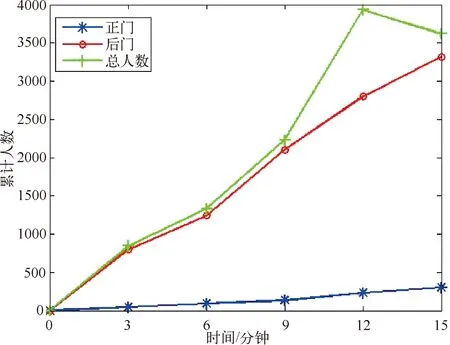
图5 1号楼学生累计数量—时间关系

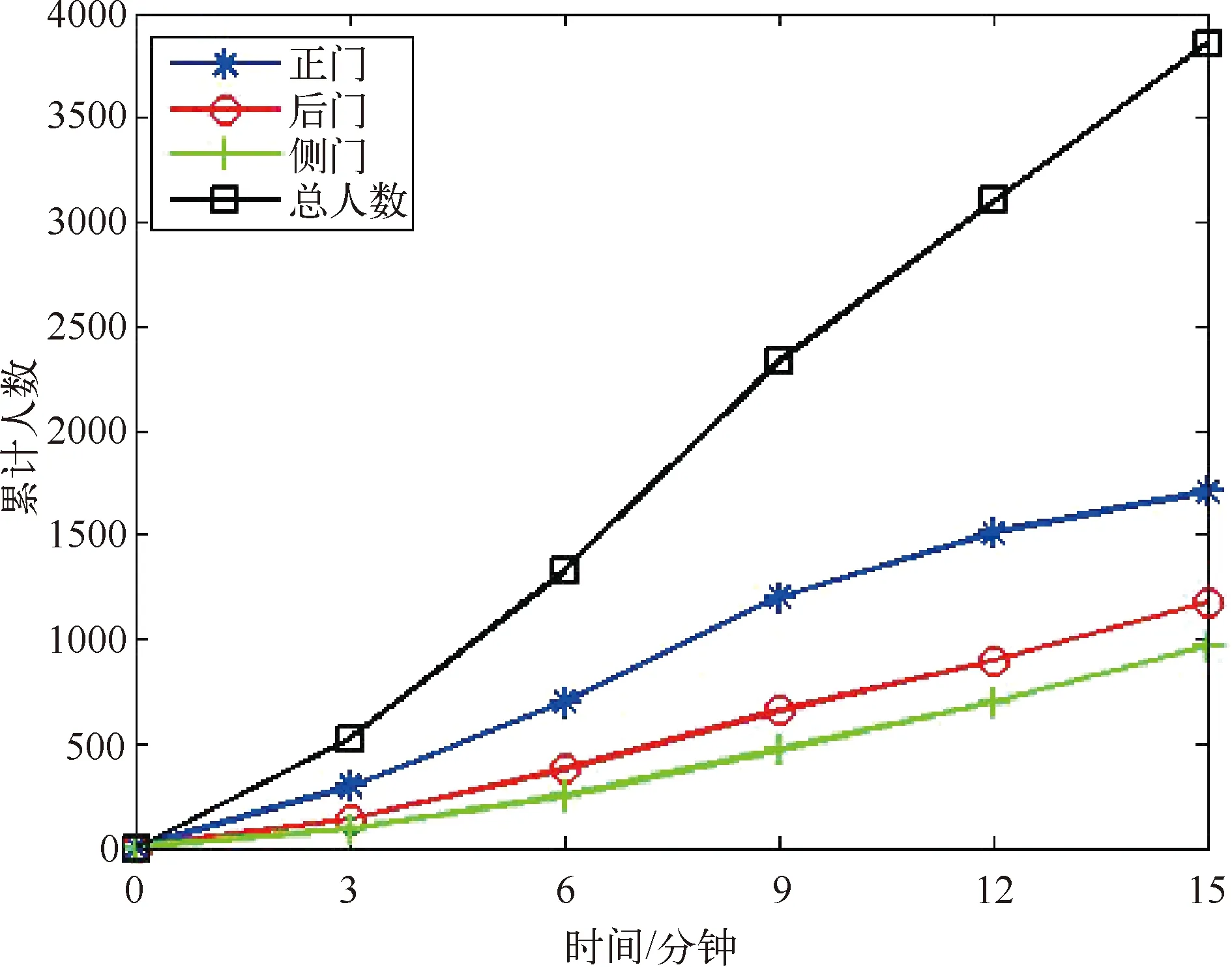
图6 2号楼学生累计数量—时间关系

图中曲线的前部分比较平缓，数值偏小，表示在下课后开始的几分钟里，大部分学生还未到达教学楼门口。随着时间的推移，数据开始上升，这个时间内学生大量走出教学楼。这些数据表明，下课后5～10分钟迎来峰值，以该时间段为仿真模拟中的时间节点，在这个时间段里，我们可以分析行人的分布情况和区域显示的热力图以便直观感受到下课后人潮峰值时道路的拥挤程度。

从教学楼走出，经过学校道路，走到食堂、宿舍等区域的最终热力图的呈现结果如图7所示：

图7 行人路线热力图

根据此图我们选择一个拥挤程度最突出的区域作为我们的研究对象。热力图中，大面积的呈深红色区域的代表着该出行人密度已经接近了或者超过了1.5 ρ/m2(比较舒适的密度为0.75 ρ/m2)。图中区域行人多已处于拥挤状态，且沿着道路的宽度方向逐渐密集分布。

由于1号楼(博观楼)正门直对学校南门，中午很少有学生去南门那边，所以博观楼后门会比较形成较大规模的拥堵。这写学生分别去往北区食堂、宿舍，小黄车和中区食堂等区域，所以下课后这个位置会出现人群十分密集现象，博观楼学生流热力图8如下所示：

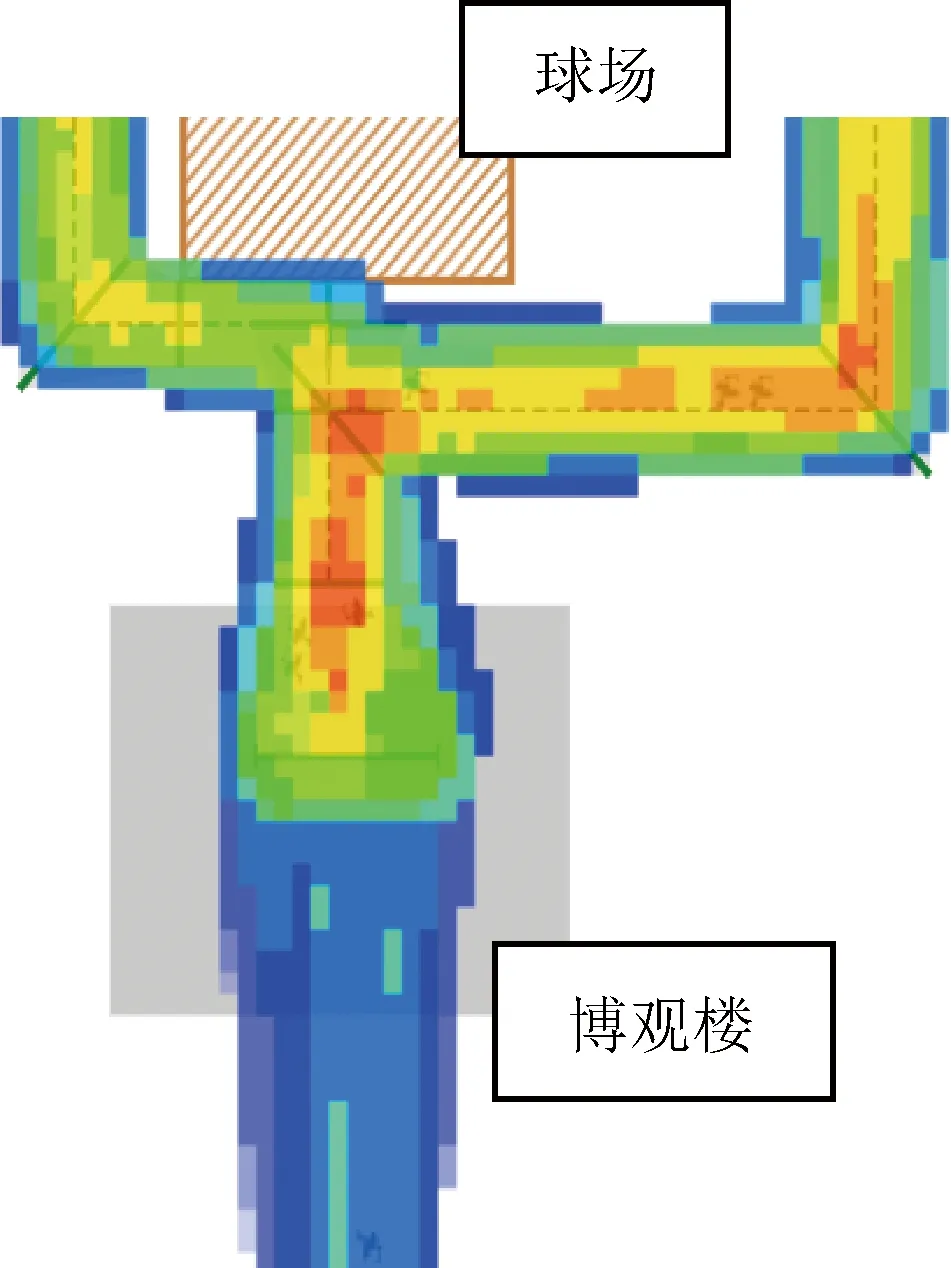
图8 1号楼学生流热力图

2号楼(致远楼)情况也是一样， 2号楼有正门，后门及侧门，侧门宽度较小，所以侧门出来的人数也就相对比正门和后门的少，选择从前门走的人占2号楼累计出来人数的大多数。2号楼的上课人数众多，教学楼有三条道路使学生分散，但是随着学生行人的扩散，周围几条道路很快被学生占用挤满，在没有得到充分疏散的同时，1号楼以及3号楼(明德楼)的学生又补充上来使得道路更加拥堵起来，于是便形成了较大规模的道路拥挤。其中还有部分汽车和自行车从中驶过，占用了一部分道路空间，路面紧张的情况进一步加剧。另一方面去北区需要经过马路红绿灯，红灯的时候，拥挤会更加明显，这使得道路情况更加拥挤不堪。因此对想去中区吃午饭而从后门出入的学生来说，这些都是不明智的道路选择。2号楼下课时的楼门区域热力图9如下所示。

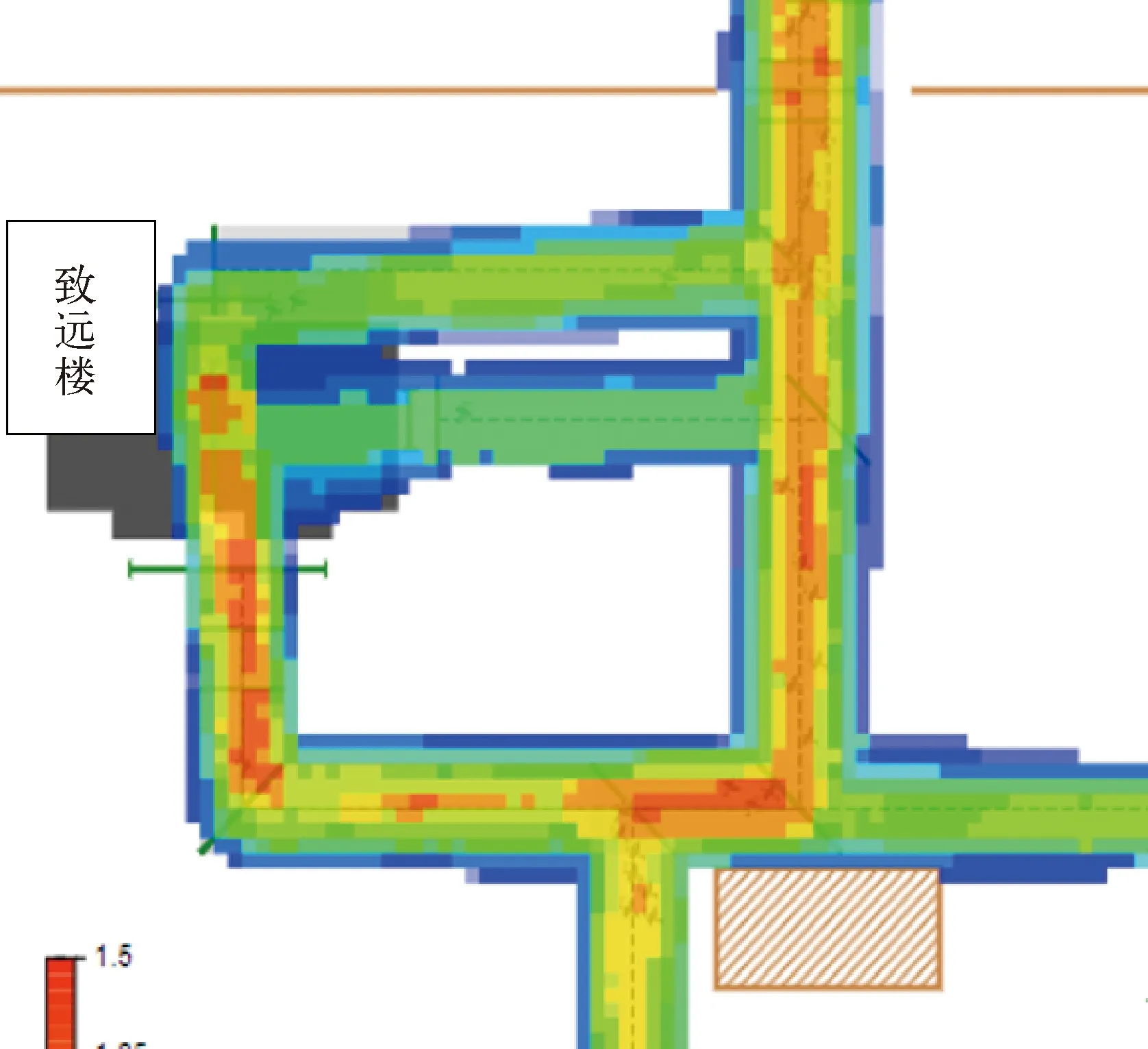
图9 2号楼学生流热力图

道路上的拥挤时间大约是在5～10分钟内，学生大量从教学楼出来是在下课后3分钟，由此可以推算出学生从教学楼走到道路拥堵区域的时间大约为3分钟左右。在这段时间内，学生离开教学区域前往食堂、宿舍等地所要经过的道路会逐渐变得拥挤起来，学生空间流动给道路状况带来不断的冲击。两股人流互相交叉，道路交汇的地方就成为了拥挤区域，而且随着人流的增加学生的移动速度也随之变得缓慢，有的地方甚至需要停下脚步等待前面的人先走。

校园道路部分区域在下课后，学生流密度大，道路处于拥挤状态，这些与学校道路宽度不无关系，如果想要加宽某条校园道路，这所要支出的经济花费和道路施工情况不但会给校方造成压力，且在施工时道路拥挤情况会更加明显且拥堵时间更长。但是可以从学校安排与管理方式上改善现状，首先，可以尽可能的分散学生上课地点，从而实现分流学生，以减轻下课时学校道路的压力，但在现实中，大部分课程需要先进行理论课接着再进行其他实验环节课程，理论课程是必不可少的一份，所以通过这种方式来减轻校园道路压力的方法达不到预期效果；其次可以在下课时管理私家车出行的方式来减轻道路压力，每当下课时，部分私家车也会随着学生流一起进入道路，而且私家车占地较大，每当私家车经过时学生不得不为其让路，这使得学生在道路的滞留时间更长，更加剧了现实中的拥堵。针对这些问题，我们还可以拉长两座教学楼下课时间的差值，相应的也可以减轻学校校园道路的压力。

教学楼各个出口宽度及目标线的上限数据值如表1所示。

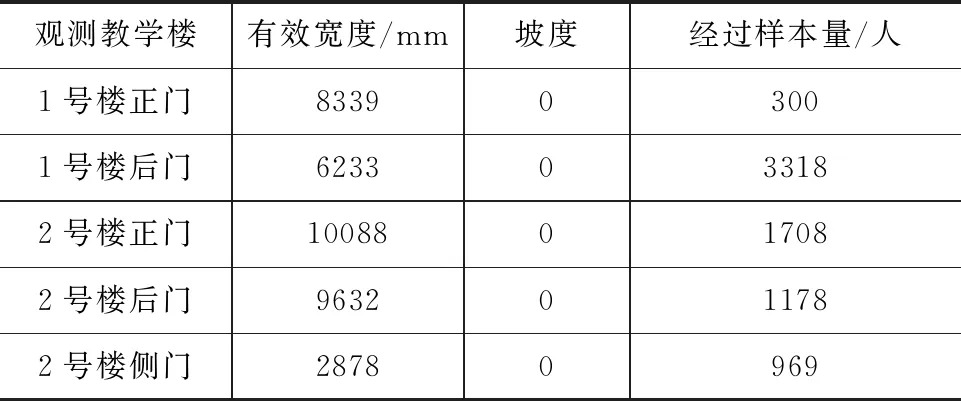
表1 被观测教学楼几何参数

3 结论

(1) 通过热力图分析，找到拥堵的主要区域，有针对性的分散学生上课地点，从而实现分流学生，以减轻下课时学校道路的压力；

(2) 可以在下课时管理私家车出行的方式来减轻道路压力，每当下课时，部分私家车也会随着学生流一起进入道路，而且私家车占地较大，加剧拥堵；

(3) 我们还可以拉长两座教学楼下课时间的差值，如可以让一个年级大部分学生在一个教学楼里上课，这样可以实现教学楼下课时间的不同。这样也可以减轻学校校园道路的压力。