IG-LSTM模型在空气质量指数预测中的应用

陈 岑，田晓丹，武文星

(华北科技学院 计算机学院，北京 东燕郊 065201)

0 引言

空气与人类的生产生活息息相关，但伴随着空气污染加重，人类生活所面临的危害也是与日俱增。研究表明，吸入过多的污染空气会导致呼吸道和肺部疾病，还会损害心血管系统和肝脏，从而严重可夺去人的生命。

目前对于空气污染预测，国内外都做了不少的研究。国内方面，张珺、王式功等[1]人利用BP神经网络结合变量筛选的方法对不同城市分季节建立了空气污染物浓度的预测模型。蒲国林，刘笃晋等[2]提出了一种由改进人工蜂群算法与反向传播算法相结合的预测方法(KABC-BP)，为空气质量评价提供了新思路，为空气污染预测提供了新的预测方法。康兵兵、党鑫等[3]使用深度栈式自编码模型进行了空气质量预测，该模型基于Java平台构建，具有良好的精度。王宝英、杨丰玉等[4]将气象因素应用于我国南昌、南京、合肥三座城市环境空气质量的监测中，并对产生的问题提出了相应的改进建议。国外方面，Ji Degang和Xie Xiaoxian等[5]利用BP神经网络与FCM对空气质量进行了预测和分析，结果表明吻合度较高。ZhongshanYang和JianWang等[6]用模糊综合评价法评估了最主要的空气污染物，提出了混合模型MCSDE-CEEMD-ENN来预测六种主要污染物的浓度。HongZheng、HaibinLi和XingjianLu等[7]针对香港和北京的PM2.5提出了一种多核学习(multiple kernel learning，MKL)模型，并使用5个指标进行了预测，结果表明预测精度均高于ARIMA和随机森林。

鉴于LSTM神经网络善于利用空气的时间相关性特点，对中长期预测的准确率较高，与其他的机器学习算法相比在处理时序数据上有明显优势，因此，文中引入LSTM神经网络对空气污染进行预测研究。通过LSTM神经网络构建空气污染预测模型，会为政府环境保护部门提供当地污染的变化趋势，有助于城市规划与建设、污染控制，对公共管理事业发展均有重要的理论意义与实用价值。

1 理论基础

1.1 LSTM模型

LSTM神经网络是基于循环神经网络(Recurrent Neural Network，RNN)的变体，对处理长期依赖问题有很好的效果[10]。LSTM神经网络继承了RNN的递归优点，可以解决RNN的梯度消失与梯度爆炸问题，其结构示意图如下：

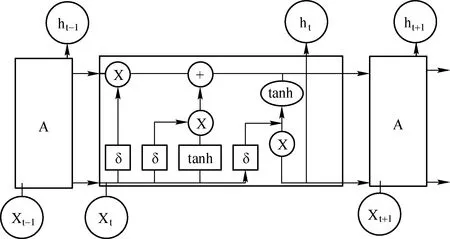
图1 LSTM结构示意图

该结构的核心思想是引入了一个叫单元状态的连接，其中最后的状态不再简单地存储，而是通过LSTM神经网络地训练机制来选择状态更新。LSTM神经网络的训练机制，就是通过“门”来控制删减或增加信息。一个LSTM单元包含3个门，分别是忘记门、输入门和输出门。

(1) 忘记门

忘记门是用来决定模型会从上一个单元丢弃什么信息，该门会读取上一个单元的输出ht-1与本单元的输入xt，输出一个0与1之间的数值ft并赋值给当前的单元状态Ct-1，数值0代表“完全丢弃”，数值1代表“完全保留”，其计算公式如下：

ft=σ(Wt[ht-1,xt]+bf)

(1)

式中，Wf是忘记门中的系数矩阵；σ表示运算函数，一般选用sigmoid函数；[ht-1，xt]表示将其中的两个向量ht-1、xt连接成一个更长的向量；bf是忘记门偏置向量。

(2) 输入门

输入门的作用分为两部分，一是在单元中找到那些需要更新的状态，二是把需要更新的状态进行迅速的更新。输入门中tanh隐层作用是要创建新的状态向量Ct，忘记门在找到需要忘掉的信息之后还需要将它与旧状态相乘，确定需要丢弃的信息。最后，将结果加上it·ct使得状态获得新的信息，其计算公式如下：

(2)

it=σ(Wi[ht-1,xt]+bi)

(3)

(4)

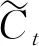
(3) 输出门

输出门，使用sigmoid隐层来确定哪个部分将输出，进而通过tanh进行处理(得到-1～1之间的值)并将它和sigmoid的输出相乘，得出想要输出的部分，其计算公式如下：

ht=Ottanh(Ct)

(5)

式中，σ是sigmoid函数；Wo表示输出门中的系数矩阵；bo表示输出门偏置向量。

1.2 信息增益

信息增益(Information gain)是非对称的，用以度量两种概率分布的差异。在信息增益中，衡量标准是特征能够为分类系统带来多少信息。对一个特征而言，系统是否拥有它的信息量将会发生变化，而前后信息量变化的差值就是这个特征给系统带来的信息量。所谓信息量就是熵(entropy)[14]。

假如有变量y，其可能的取值有n种，每一种取到的概率为pi，那么y的熵为：

(6)

式中，p(yi)代表事件发生的概率；logp(yi)代表概率分布的对数。由式(5)可知，y可能的变化越多,x所携带的信息量越大，熵也就越大。对于分类和聚类问题，属于哪个类别的变化越多，类别的信息量越大。所以特征T给分类或者聚类C带来的信息增益为：

IG(T)=H(C)-H(C|T)

(7)

式中，H(C|T)是条件熵的C给属性的值T，H(C|T)包含2种情况：一种是特征T出现，记为t；一种是特征T不出现，记为t,所以有：

H(C|T)=P(t)H(C|t)+P(t，)H(C|t，)

(8)

再由熵的计算公式便可推得特征与类别的信息增益。

2 LSTM网络模型的构建

2.1 选择模型拓扑结构

LSTM网络模型一般包含：输入层，输出层和隐含层三个部分。根据想要达成的目标与需求不同，中间隐含层的层数是不固定的，可以动态的变化，隐含层的层数越多，模型的非线性转换能力越强，但同时，也会增加模型的复杂度。因此，为了降低模型复杂度，常见的LSTM模型一般只有一个隐含层[8]。本文模型设计中选择了一个隐含层的形式。

2.2 确定各层维数

各层维数即是各层处理的数据变量的个数，输入输出层的维数大小取决于实际问题的数据维度。例如若设定影响空气质量指数(AQI)的主要因子包括CO、SO2、CO2、O3四个，则输入层维数设置为4，若输出层只需输出下一个时刻的空气质量指数(AQI)，则输出层维数设置1。而隐含层维数确定相对复杂，通常根据经验公式与逐步试错法结合的方法确定。首先利用经验公式确定隐含层维数的大概范围，再利用逐步试错法，比较不同节点数情况下隐含层预测性能，选择误差最小、性能最好的模型维数为隐含层的维数，可通过如下经验公式计算[12]。

(9)

式中，a表示输入层的节点个数；b表示输出层的节点数；c为1～10之间的正整数；q为隐含层节点数。

2.3 学习速率的确定

LSTM中确定学习速率的方法主要有两种：固定学习速率法和退化学习率法。其中固定学习速率法则主要依据经验选择，选取的范围在0.05～0.5之间。退化学习率法一般在起始阶段设置一个较大的学习速率，通过训练不断的调整学习速率，可保证训练初期的效率，又可以通过调整实现训练精度的提升。在此学习速率的衰减速度由迭代循环计数变量(global step)和衰减步长(decay steps)来决定，具体的计算公式如下[12]：

p=x·yz

(10)

式中，p为所求学习速率；x为初始的学习率；y为衰减系数；z为迭代循环计数变量与衰减步长的比值。

3 LSTM网络在C市空气质量预测上的应用

3.1 C市空气质量的污染特征

结合C市的地理位置、气候特征等环境因素，并根据2014年到2018年C市空气质量的总体情况进行简要分析。

(1) C市地形、气候特征

C市位于河北省中部、华北平原中东部，北临首都北京，东与天津交界，地处京津冀城市群核心地带和环渤海腹地[9]。受地质构造的影响，该市大部分处于凹陷地区；由于地处中纬度地带，长期受到温暖带大陆性季风气候影响，因此四季分明。夏季炎热多雨，冬季寒冷干燥，春季干旱多风沙，秋季秋高气爽。根据历史资料显示，年平均气温为11.9℃，年平均无霜期为183天左右，全市年平均降水量为554.9毫米。

(2) C市空气质量总体概况

使用Python对C市2014年1月1日至2018年12月31日的空气质量AQI指数进行对比分析，得到基于时间序列的分析折线图，如图2所示：

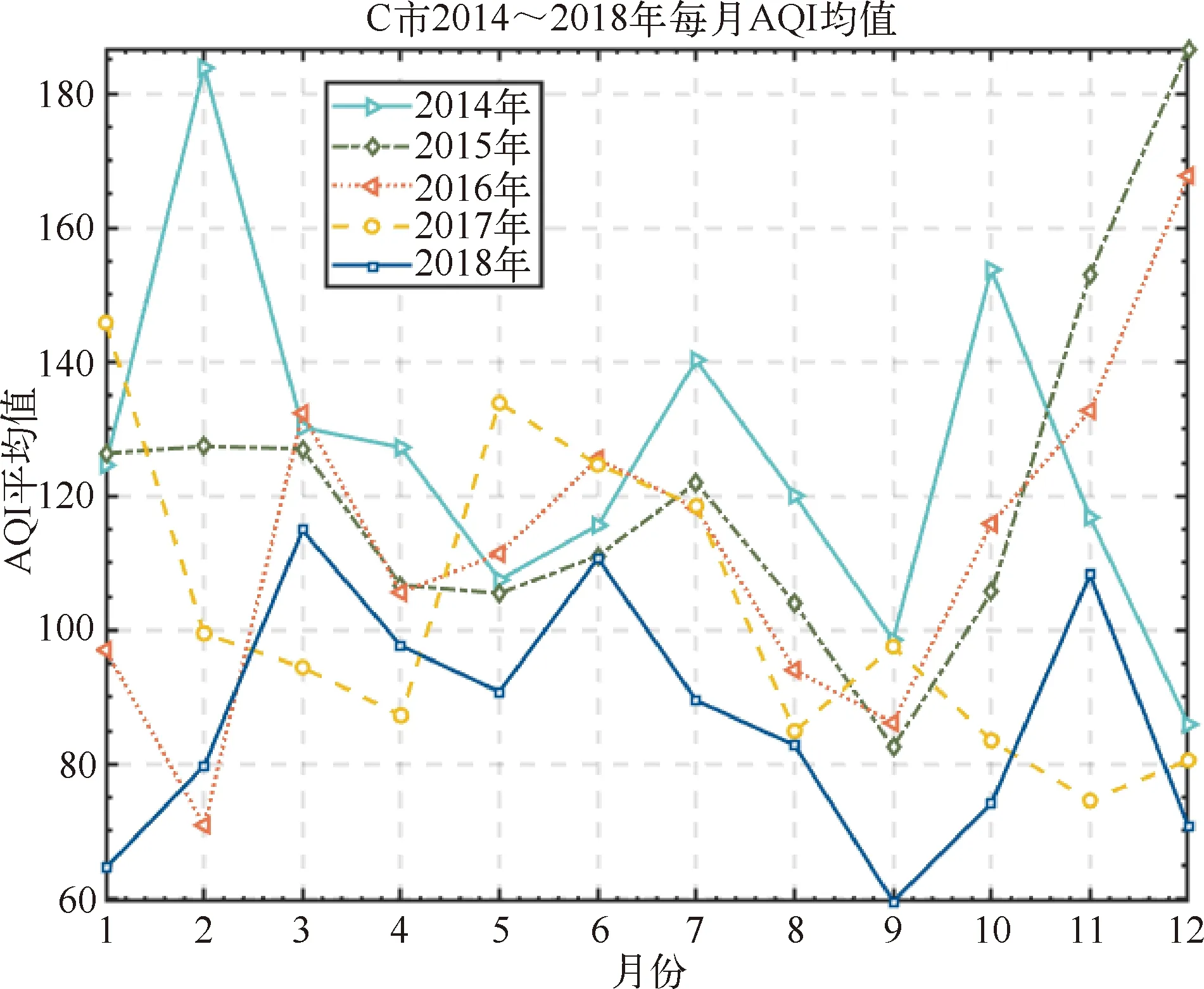
图2 C市5年月度空气质量指数均值比较

从图2中可以看出，C市空气质量AQI指数的分布有一定的季节性波动，每年的冬季AQI指数较高，空气质量较差。通过分析发现，主要是因为C市冬天天气寒冷，居民的取暖需要燃煤，大量的煤炭燃烧导致空气中的污染物增加，并且C市冬季天气干燥，降雨量少，使得地表植被覆盖率低，水土的固着能力差，空气中扬起的细颗粒物增多，进而导致C市冬天的空气质量较差。从图中还可以发现，该市历年10月份的AQI指数也存在偏高的问题，分析研究后，发现主要是因为每年的10月假期较多，节假日出行车辆增加，造成污染物排放量增加，因此2014年10月中度污染及以上有19天、2015年有20天、2016年有16天、2017年有18天、2018年有19天。从C市空气质量的同比来看，2014～2018年，空气质量没有很明显改善。

3.2 利用信息增益筛选输入因子

在使用LSTM建模之前，需要对数据进行分析，判断各特征(AQI、质量等级、PM2.5、PM10、SO2、CO、NO2、O3_8h)的数据分布及其之间的关系，本文首先利用信息增益方法(Information gain)计算出8个输入特征变量对输出特征变量AQI的贡献，其次利用Pandas散布矩阵函数(scatter_matrix)及相关系数函数(corrcoef)对数据集特征及其关系进行了辅助分析验证。

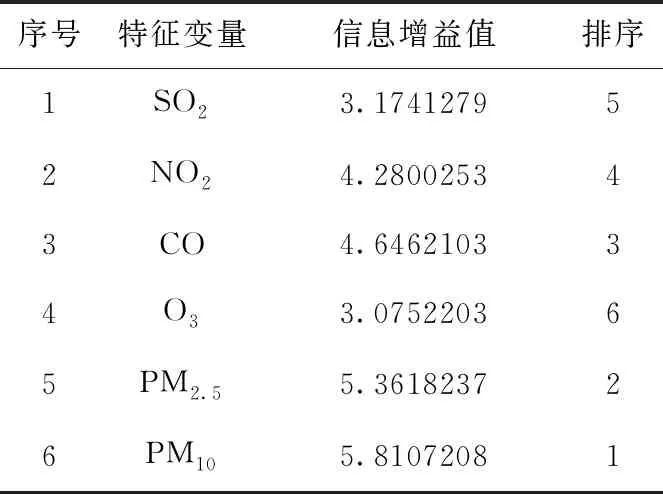
表1 输入特征变量的信息增益值比较

从表1可以看出，PM10、PM2.5对输出变量AQI的影响力最大，其次为CO、NO2，对输出变量AQI影响力最小的为SO2、O3。通过对输入特征变量的信息增益值比较，可选取PM10、PM2.5、CO、NO2作为预测模型的输入特征。为了保证实验的准确性，下面采用Pandas散布矩阵函数(scatter_matrix)及相关系数函数(corrcoef)进行辅助分析。

图3是SO2，NO2，CO，O3，PM2.5，PM10变量散布矩阵分布图。如图中所示，SO2，NO2，CO，O3，PM2.5，PM10散布矩阵图呈对称结构，除对角上的密度函数图之外，其他子图分别显示了不同特征列之间的关联关系。如AQI与质量等级、PM2.5和PM10之间近似成线性关系，说明这些特征之间线性关联性很强；AQI与SO2、CO、NO2之间关系次之；相反地，AQI与O3_8h特征列之间的散布状态比较杂乱，基本无规律可循，说明各特征之间的关联性不强。分析数据集各特征(列)之间的关系时，散布矩阵能以图形的形式“定性”给出各特征之间的关系，如要进一步“定量”分析，则需要使用皮尔逊相关系数。图4皮尔逊(Person)相关系数定量显示了各变量之间的皮尔逊相关系数的值。综合图3和图4可以得到：

图3 Pandas散布矩阵函数

图4 Person相关系数

(1) AQI与质量等级、PM2.5和PM10之间相关系数的值均在0.9以上，相关性较大；

(2) AQI与SO2、CO、NO2之间相关系数的值均在0.6以上，相关性较为居中；

(3) AQI与O3_8h的相关系数为负数，负相关性较小。

这与信息增益方法(Information gain)分析基本一致。因此，O3_8h特征应予舍弃。虽然每种污染物与空气质量AQI指数相关性存在差异，但都有一定的关联，故将质量等级、PM2.5、PM10、CO、NO2作为模型的输入特征，AQI指数作为测试标签(label)。

3.3 数据标准化方法

在数据训练之前需要对数据进行标准化处理，数据标准化即将原始数据按照一定的比例缩放到更小的区域中，例如[0,1]或者[-1,1]区间[11]。数据标准化主要目的是为了数据处理的方便，消除变量之间的量纲关系，从而使数据具有可比性。常见的数据标准化方法包括Z-score(正规化方法)和Min-max(规范化方法)等，本文采用Z-score标准化处理，具体算法和公式如下所示：

y=(x-mean(x))/std(x)

(11)

式中，y是归一化之后的数据；x是原始数据；mean(x)表示原始数据的均值；std(x)表示标准差。

3.4 确定网络的拓扑结构与参数

本文模型采用三层网络拓扑结构(即一层为输入层，一层为输出层，中间包含一个隐藏层)实现C市未来空气质量指数的预测。根据3.2中的因子筛选分析，剔除了O3_8h，将PM2.5、PM10、SO2、CO、NO2作为模型的输入特征，故输入层维数设置为5。输出层维数设置为1。

由于隐含层维数对模型的预测误差影响较大，首先根据公式(5)确定隐含层维数的试凑范围[13]，在本文中，模型输入层的维数a取值为5，输出层维数b取值为1，c为1～10之间的整数，故最终隐含层维数q区间为4～13，表2列举了隐含层维数取不同数值时，平均绝对误差MAE(Mean Absolute Error)的取值情况。

表2 隐含层维数对预测性能的影响

表2所示，C市空气质量指数预测模型的隐含层维数取值为10时，预测误差最小，故在本文中隐含层维数取值为10。

4 实验设计及结果分析

本实验将LSTM模型和信息增益模型相结合，这就是AQI混合预测模型，其框架如图5所示。首先将输入特征变量进行信息增益计算，然后通过对比筛选出信息增益值较大的输入特征变量，然后利用Pandas散布矩阵函数(scatter_matrix)及相关系数函数(corrcoef)对数据集特征及其关系进行了辅助分析，最后将挑选出的输入特征变量输入LSTM模型预测空气质量指数AQI。实验数据使用C市2014年至2018年真实监测数据，将该数据集分成两部分，分别用于模型训练和测试。其中选择前80%作为训练集，后20%数据为测试集。设定每批次训练样本数(batch_size)为10,时间步长(timesteps)设置为3，学习速率采用退化学习率法，初始化学习速率为0.15，衰减系数为0.9，衰减速度为50。

图5 AQI混合预测研究框架

使用PM2.5、PM10、CO、NO2作为预测AQI空气质量等级的强关联因子，模型经过多次训练后，得到预测值(绿色)与真实值(红色)的曲线对比图，如图6所示。模型损失(loss)变化趋势如图7所示。

图6 真实值与预测值曲线对比图

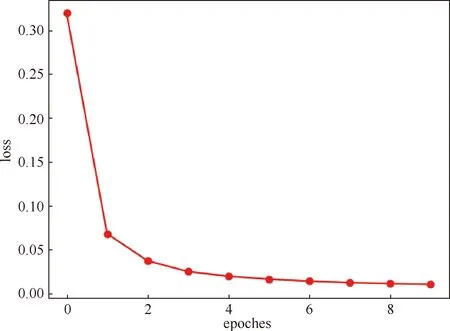
图7 损失变化趋势图

此时，得到如表3的C市空气质量指数AQI在IG-LSTM模型下的误差分析：

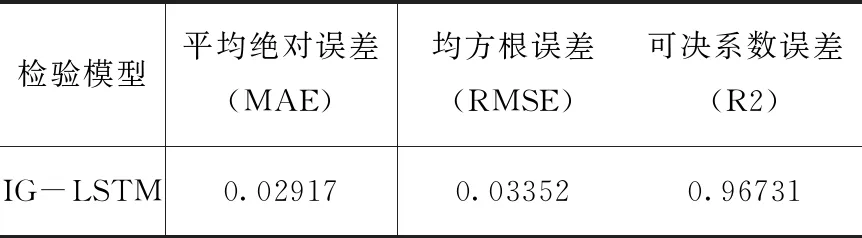
表3 AQI指数误差分析

从图5和表3可以看出，该模型的拟合度较高，IG-LSTM模型的平均绝对误差与均方根误差均在0.1之间，可决系数误差趋近于1，虽然在个别点的四周有较大的误差，但AQI的展望值与现实值在整个趋势上基本保持一致，并且网络训练结果的精确度与网络检验的结果差别不大。此外，图6中横坐标表示时间，但由于数据单位为天，数据量较多，若全部显示会导致真实值与误差值对比不明显，所以这里做了简化处理，取时间间隔为半年来显示对应的均值AQI。图7为模型训练过程中的损失变化，从图中可以看出在模型刚开始训练时损失值较大，达到了0.33。大约在epochs取1时出现第一个拐点，此时损失值较初始值有较大幅度下降，下降到了0.06左右，由此可以看出误差收敛速度迅速。而在epochs=2与epochs=4期间，训练误差仍有缓慢下降趋势，训练过程误差收敛域更窄，最终趋向于平缓，无限趋近于0。由此说明，本文模型收敛速度快，优化过程稳定性好。

为了验证IG-LSTM模型处理时序性指标的有效性，本文将IG-LSTM算法与BP神经网络算法、LSTM神经网络算法进行了对比分析。在实验中，BP神经网络同样采用了3层网络结构，隐含层维数为10，对比结果如表3所示。

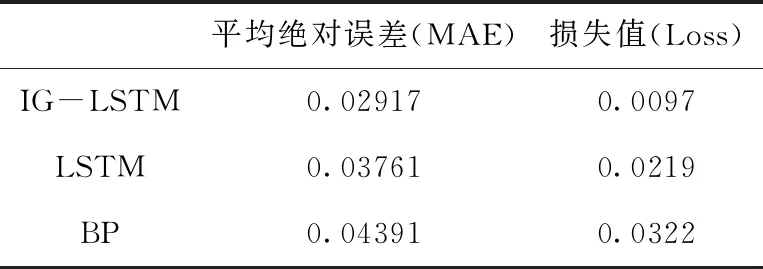
表4 三种方法的预测模型性能比较

从表4可以看出，采用IG-LSTM算法的预测模型在平均绝对误差和损失值上都优于BP算法和LSTM算法。

5 结论

(1) 通过对C市空气监测数据的分析入手，进而引入IG-LSTM模型实现C市空气质量指数AQI的预测，并与采用BP神经网络、LSTM神经网络的预测模型进行了对比研究。实验结果表明，利用IG-LSTM的空气质量预测模型与传统BP预测模型、LSTM预测模型相比，在预测结果与迭代时间等方面都具有明显优势，具有更低的预测误差和损失值。本文的研究成果为空气质量指数AQI的预测研究提供了一种新的思路，对提升C市空气质量的预测水平，为空气质量的预测报警提供辅助。

(2) 由于空气质量指数AQI的影响因素较多，在预测C市未来的空气质量状况时，没有考虑到除了SO2、NO2、CO、O3、PM2.5、PM10污染物以外的天气环境的影响，以及节假日车流量的大小，国际会议的举行，风速的变化等因素。因此，要进一步提高精准度，应该考虑这些因素的影响，这将是下一步研究方向。