基于贝叶斯决策的超密集异构网络切换研究*

（重庆金美通信有限责任公司，重庆 400001）

0 引言

由于用户需求的不同和网络构建成本的差异等，目前通信网络的组成不再是一个单一的系统，而是由多种不同性质（包括WiFi、WiMAX、UTMS、WLAN、Bluetooth、3GPP 以及Advanced LTE 等）的网络融合而成的一个通信系统[1-3]。因此，将各种网络资源融合并充分发挥各自的优势，将是下一代通信系统发展的一个必经阶段。各种不同的网络通过全IP 的设计实现网络融合，从而给用户提供随时随地的接入，以满足用户的不同需要。但是，这造成了网络复杂度的增加和网络管理难度的增大[4]，也造成了移动用户在不同覆盖区域的网络之间的切换问题。

针对该问题，结合已有研究成果，提出了一种利用区域感知的贝叶斯策略[4]，以解决不同网络之间切换的设计方案。该方案通过用户在网络中的位置计算用户接入各个网络的概率，并依据贝叶斯定理计算接入的贝叶斯概率，然后选择贝叶斯概率大的作为移动用户要切入的网络。该方案降低了用户在超密集异构网络中切换错误的概率，提升了网络性能。

1 系统模型

假设有A 和B 两个异构网络，且A、B 相邻，M 表示移动用户，移动用户切换到A、B 两个网络的概率表示为P(A)和P(B)，则移动用户M 切换到A、B 两个网络的条件概率则为P(M|A)和P(M|B)。移动用户M 在当前位置切换的概率为P(M)[4-5]，则有：

可知，用户M 进行网络切换时有A、B 两个网络可以选择。用户M 到底切换到哪个网络，则可以用贝叶斯定理进行决策。

根据贝叶斯定理，得：

也就是说，当移动用户M 进行网络切换时，如果概率P(A|M)＞P(B|M)，则移动用户切换到A 网络；反之，用户切换到B 网络。

2 算法设计

假设X为某一时刻需要进行切换的用户，X=[x1,x2,…,xn]T，X∈Rn。B表示用户所在区域内部署的基站，B={w1,w2,…,wn}。建立移动用户X和所处的网络的切换映射Rn→B。

按照基站的覆盖区域计算，P(ωi,j)表示在基站j的覆盖范围内移动用户i的切换概率，表示为：

在基站j的覆盖范围内用户i发生网络切换的概率可以表示为[6-7]：

用户X为需要切换的用户，依据贝叶斯推理得到需要切换到可能服务网络的概率，可以表示为：

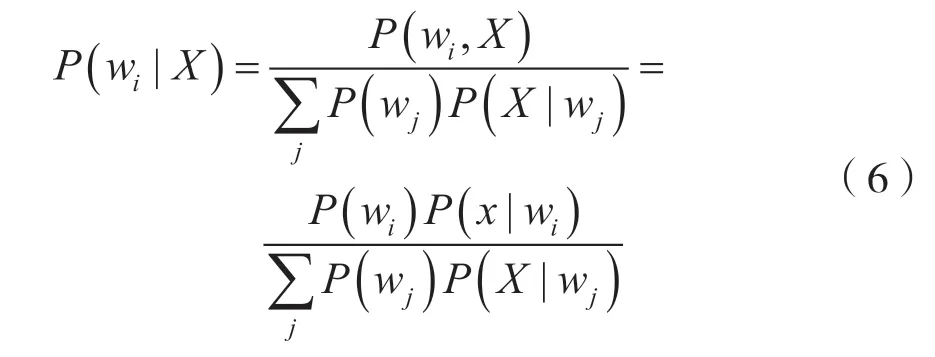
3 超密集异构网络切换的贝叶斯决策

将N个异构基站随机部署在区域S内，其中5G 基站位于该区域中心，5G 基站的覆盖半径为R0，集合R={R1,R2,…,Rn} 表示异构基站的覆盖半径。异构基站在覆盖区域内坐标集合为(X,Y)={(x1,y1),(x2,y2),…,(xn,yn)}。假设用户MS 坐标为(x,y)，则用户MS 同第i个基站的距离表示为：

假设部署的N个异构基站的集合用{H1,H2,…,HN}表示，第i个网络表示为Hi，i∈(1,2,…,N)。根据式（4），Hi基站覆盖下移动用户M 的概率可以表示为[8]：

式中，移动用户M 到基站i的直线距离表示为di，基站i的覆盖半径表示为Ri。基站Hi下移动用户切换的条件概率表示为P(X|ωi)，i∈(1,2,…,N)。那么，在所有基站覆盖区域下移动用户M 切换的全概率表示为：

根据式（9），用贝叶斯定理计算移动用户M在各网络之间切换的概率为：

依据式（10）得到超密集异构网络的决策函数（Decision Function，DF）为：

DF的最大值即用户MS 要选择接入的网络。

文中采用最大似然估计设计其中的参数。假设P(X|wi)服从独立的指数分布，由于参数θ未知，故建立θ同条件概率P(X|wi)的关系，用P(x|wj,θj)，j=1,2,…,m表示。由于在基站的覆盖区域移动用户M 的位置是独立的，故建立θ的似然函数为：

式中，参数θ是用户MS 在基站覆盖区域内的位置X的函数。

4 仿真场景设计

仿真场景的网络模型如图1 所示。在仿真场景内，各异构网络有重叠。在此场景中，di表示移动用户M 到基站的距离，Ri表示各基站的覆盖半径，基站覆盖区域面积是500 m×500 m。本文的仿真采用定量分析，基站数为9 个。

图1 仿真场景及用户移动轨迹

如图1 所示，当移动用户M 沿着图1 中的轨迹穿过覆盖范围不同的基站时，假如移动用户M 从位置1 移动到位置4，当移动用户M 在位置1 时，完全在H1的覆盖范围。基站切换概率P(X|ωi)最大的是H1，表明基站覆盖范围内距离用户越近，基站切换的概率越大。同理，用户在位置2 和位置3 时切换概率P(X|ωi)最大的是H4。

5 仿真及结果分析

根据公式计算用户MS 在不同位置的切换概率，结果如表1 所示。

表1 不同位置的切换概率

可以看出，当用户移动到位置4 时，处于H4的边缘上，但是在H3和H7两个基站的重叠覆盖范围内。根据运行轨迹可知，此时移动用户M 离开了基站H4的覆盖范围，进入到基站H3和H7的覆盖范围，且已经触发切换机制。

根据表1 画出MS 在不同位置时基站的切换概率P(X|wi)的变化情况。当用户MS 在位置4 时，根据式（8）计算切换概率P(X|w4)=0.59 最大。当移动用户M 离开H4基站，引发基站切换后进入到其他的服务基站内。此时不能再包含H4，而基站H3和H7是要选择切换的基站。利用贝叶斯决策概率，得P(w7|X)＞P(w3|X)。因此，选择贝叶斯决策概率值最大的基站作为目标服务基站进行切换，因此应该切换到基站H7。

从图2 中可以看出，基于区域感知的超密集异构网络在切换时，引入贝叶斯模型作为判据能够使移动用户M 在切换时选择最优的服务小区。

图2 用户在不同位置时基站的切换概率

6 结语

针对用户在超密集异构网站中的切换问题，提出了一种基于区域感知的贝叶斯策略。首先在计算超密集异构网络的切换概率时引入贝叶斯决策，建立基于区域感知的贝叶斯数学模型，其次详细介绍超密集异构网络在切换时引入贝叶斯决策的规则，最后搭建仿真环境对其进行仿真。通过对场景中移动用户位于不同位置的切换概率分析可知，在超密集异构网络进行切换时，引入贝叶斯决策提高了网络之间切换的准确性。仿真结果表明，提出的切换策略不但能够确保移动用户在进行网络切换过程中选择最优网络，而且降低了切换出错的概率和能耗。综上所述，基于超密集异构网络切换问题使用贝叶斯原理是一种新的探索，具有很高的实用价值。