基于稀疏图码的混合稀疏线性回归参数估计*

（陆军工程大学，江苏 南京 210007）

0 引言

稀疏线性回归和混合分布学习在统计、信号处理和机器学习中都是非常流行的问题。混合稀疏线性回归是混合模型和稀疏线性回归的合成。目前高斯混合和子空间聚类等在混合模型和隐变量模型具有良好的表达性和灵活性，被广泛应用于背景建模[1]、说话人识别[2]和推荐系统[3]等问题。稀疏线性回归与稀疏表示和压缩感知[4]都紧密相关。作为一种新的信号表示和采集框架，它可以通过信号的稀疏表示从低维线性测量中恢复高维原始信号。在稀疏信号重构的领域中，通常需要从信道采样数据中恢复原始信号，这个过程可以被称作“回归重构”。可以通过稀疏学习找到一个满足稀疏特性的映射矩阵，然后可以通过重构算法对原始信号进行精确地重构，使信号的原始特征在低维度的样本中恢复出来。回归重构过程需要从测量值矢量y和稀疏矩阵H恢复原始高维信号x，对应的线性系统为y=Hx。

可以将这个问题进行适当建模转化为混合稀疏线性回归的参数估计问题。混合模型的参数估计通常需要较大的样本量，并且需要对算法进行多次重新初始化才能获得可接受的精度。该问题的大部分工作是提出新的算法从不同的角度对混合模型进行参数估计，并有效降低时间复杂度和样本复杂度。在文献[5]中，通过研究使用期望最大化（Expectation-Maximization，EM）算法来进行混合模型的参数估计。文献[6]针对稀疏的性质提出了一种“ ℓ1-惩罚项EM 算法”。由于似然函数的非凸性，EM 算法的理论分析比较困难。文献[7]采用EM 算法对参数估计进行了研究。对EM 算法、分类EM 算法和随机EM 算法这三种方法在模拟数据集上性能(计算量、估计量的统计特性和拟合优度)的模拟研究进行了比较。结果表明，不同方法的选择在本质上取决于算法初始化时参数的正确配置。文献[8-10]证明了给定EM 算法合适的初始化，然后进行混合模型的参数估计，可使样本的复杂度为O(npolylog(n))。该算法主要使用网格搜索初始化的步骤来确保EM 算法可以找到全局最优解。文献[11]中的算法利用张量分解技术，但是存在O(n6)的高样本复杂度的问题。利用编码理论进行参数估计的方法在近年来也被相继提出，许多现代信息论的纠错码，例如通信问题中用于纠错的低密度奇偶校验码（Low-density Parity-Check，LDPC）和极性码[12]，它们利用样本的冗余来实现鲁棒性，并使用对稀疏矩阵的结构化设计，根据LDPC 码在擦除信道中的PD 译码算法[13]来实现快速解码。

然而这些算法在稀疏信号回归重构的过程中会存在硬件上难以实现、存储空间耗费大以及重构时计算复杂度高等问题。因此，本文基于信息论的相关知识来进行查询矩阵的构造和重构算法的设计。以测量的效率、重构算法的复杂度、噪声鲁棒性等方面为研究点来对基于稀疏图码理论的混合稀疏线性回归参数估计问题展开研究。

1 基于稀疏图码的查询矩阵构造及重构算法设计框架

本节内容研究了基于稀疏图码的混合稀疏线性回归参数估计问题。首先介绍了该问题的模型，然后基于稀疏图码的理论进行查询矩阵的构造以及重构算法的设计。

1.1 问题模型

混合稀疏线性回归是混合模型和稀疏线性回归的合成。混合稀疏线性回归模型的参数估计问题模型如下：

对于混合稀疏线性回归模型，有α(1),…,α(s)∈Cn这样S个未知稀疏参数向量，一共有K个非零元素。线性测量值yi由公式(1)形式获得，每一个都是从未知类别si的稀疏参数向量中随机产生，这里的类别指代不相同的参数向量α(s)。当S=1 时就是前面提到的稀疏线性回归系统模型。

式中，xi表示查询向量，每个查询测量对(xi,yi)是从S个可能的模型中以概率qs,s∈[S]随机选择的稀疏线性模型(1)生成，概率qs称为α(S)的混合权重，满足。假设参数向量中非零元素的总数为K。在本文的后续工作中，目标是在低样本和计算复杂度的情况下有效地估计参数向量。这个问题需要同时解决从不同的S中恢复类别si以及恢复稀疏向量α(s)的非零元素的位置和值。

1.2 基于稀疏图码的查询矩阵构造和重构算法设计

混合稀疏线性回归参数估计的过程是通过精心设计的查询矩阵x来检测具有S个稀疏参数向量α的所有K个非零元素的位置和值。查询矩阵x可以通过精心设计的总和校验和比值测试来完成，然后通过逐步迭代分离算法可以恢复出所有非零元素。

总和校验。假设独立于Cn上的某个连续分布生成两个查询向量x1和x2，以及第三个形式为x1+x2的查询向量。则可以获得(x1,y1)(x2,y2)(x1+x2,y3)三个查询测量对，y1,y2,y3为对应的测量值。通过检查测量的总和，如果y3=y1+y2，那么可以得出这三个测量值是由相同的参数向量α(s)产生。在这种情况下，可以将{y1,y2}视为一组测量值对。

比值测试。该过程通过对查询向量的结构化设计来查找α(s)中非零元素的位置和值。考虑求和检查中提到的一组测量对{y1,y2}和对应的查询向量x1,x2。通过对查询向量进行设计，使α(s)中非零元素的位置信息编码在y1和y1的相对相位中。具体地，根据傅立叶矩阵变换的几何解释的思想，首先生成n个独立同分布的随机变量bj，j∈[n]均匀分布在单位圆上。让W=ei×2π/n，设置第j个查询向量的x1和x2如下：

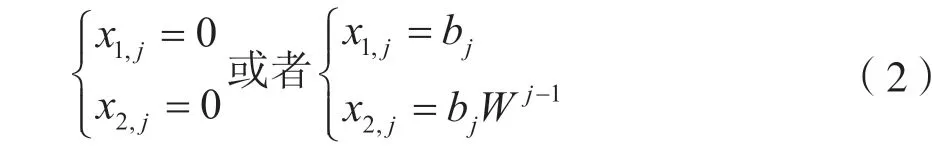
接下来，通过一个简单的例子来阐述如何利用这种设计的查询向量来查找非零元素的位置和值。假设α(1)是一个具有三个非零元素的稀疏参数向量，α(1)=[* 0 * 0 0 * 0]T，根据公式(3)的运算结果，可知测量值y1和y2的结果只与参数向量α(1)中的第四个非零元素有关。此时，这组测量值对{y1,y2}称为单节点，可以通过比值测试y1/y2的相对相位的完整性来检测单节点。

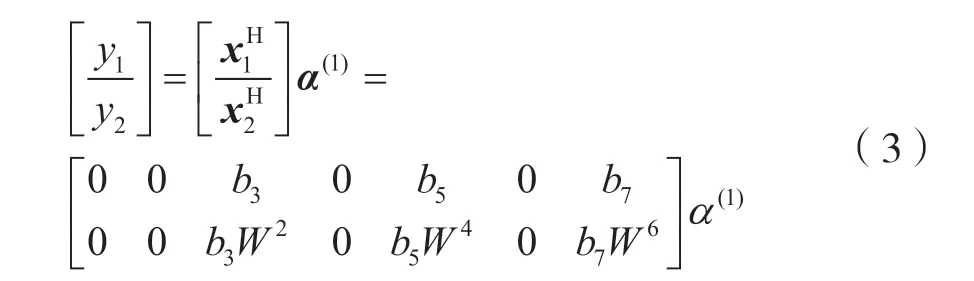
逐步分离。经过比值测试，已经发现了一些单节点，然而要找到所有的非零元素的位置，要通过迭代减少问题，减去已经恢复的元素，并找到其他非零元素。剥离的过程如图1 所示：

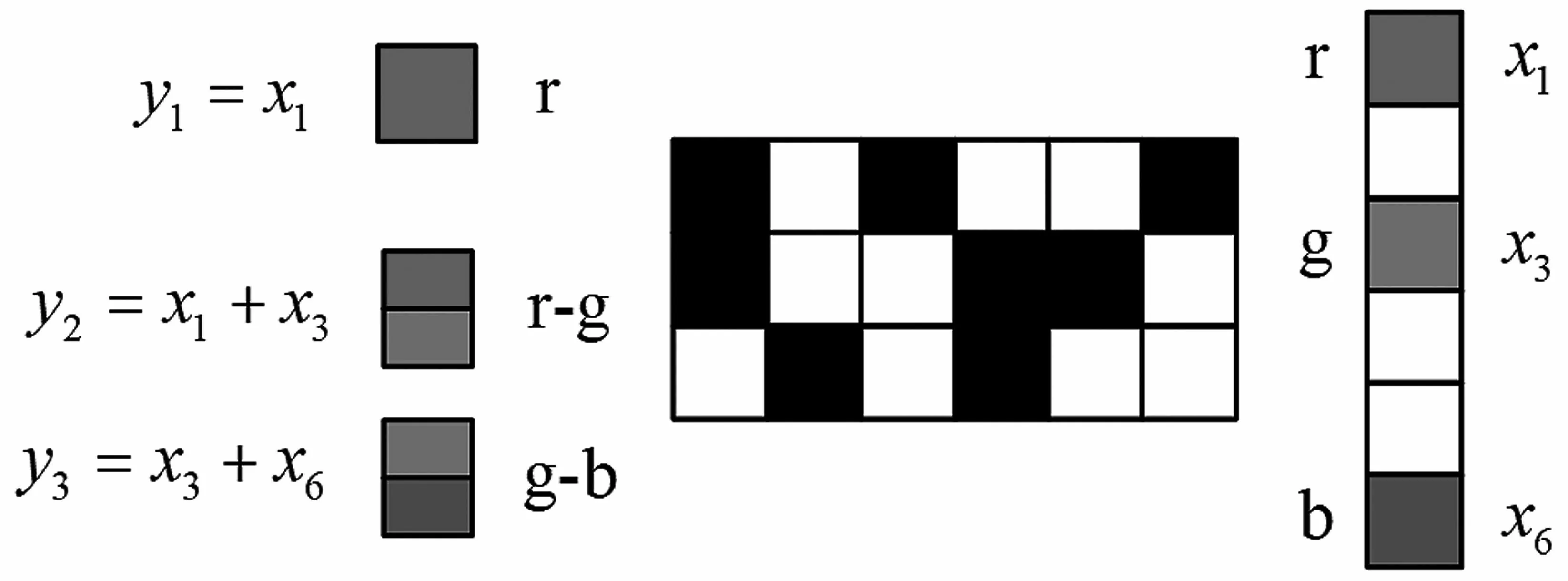
图1 逐步迭代分离示意

图1 给出了一个简单的例子，简要说明了逐步迭代分离算法如何在公式(1)中恢复参数向量α(s)，其中参数向量维数为N=6，查询向量维度M=3，α(s)中的非零元素为x1,x3,x6，查询矩阵x如下：

如图1，α(s)是含有三个非零元素的参数向量，表示为最右边方块x1,x3,x6，分别表示为r,g,b。此外，在查询矩阵x中，零元素为白色，非零元素为黑色，运用比值测试检测到测量值y1=x1。然后，从测量值y2中减去y1中对应的x1，从而检测到x3。同理，x6在x3被移除后也能被检测到。至此，参数向量α(s)中所有的非零元素均已找到。

在图2 中，给出了一个基于稀疏图码构造查询矩阵的具体例子：n=5，m=3，d=2。在图2 中，a表示d-左正则二分图，b表示查询矩阵中第一行的查询向量的设计，得到的查询矩阵如下：

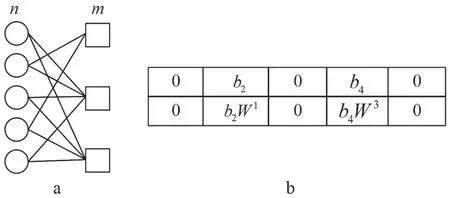
图2 基于稀疏图码的查询矩阵构造示例

通过逐步的迭代分离算法可以实现混合稀疏线性回归的参数估计。该算法的伪代码如表1 所示。

表1 基于稀疏图码的逐步迭代分离算法

2 实验结果分析

通过仿真实验测试逐步迭代分离算法的样本和时间复杂度。该实验的主要目的在于验证之前提出的基于稀疏图码的查询矩阵构造及重构算法设计的有效性。通过设置每一个稀疏参数向量α(s)具有相同的稀疏度，即它们具有的非零元素的个数相等，qs=1/S。该实验参数向量中的非零元素由高斯分布产生，具体地，通过随机产生信号长度为N，稀疏度为K的原始混合稀疏信号，对应于长度为N的稀疏参数向量，然后通过设计的算法对原始信号进行恢复。

在第一个实验中，根据不同测量值对的总数m和原始信号的稀疏度K，将采样率表示为L=m/K，分别在S=2，S=3，S=4 的稀疏参数向量中进行参数估计，根据d-左正则二分图构造的查询矩阵，设置不同的d和采样率L，来测试成功重构信号（恢复出每一个α(s)中的非零元素）的成功率。图3 展示了在100 次实验下不同采样率对应的成功重构信号的概率。从图3 中可以发现，随着稀疏参数向量的个数S的增大，成功重构信号所需的采样率也会逐步增多，并且对于有相同的稀疏参数向量个数S，其成功重构信号的概率随着稀疏度K的增大并不会有太大的变化。

图3 成功恢复概率

在第二个实验中，通过设置不同信号长度N的原始混合稀疏信号和不同的d-左正则二分图，分别在S=2，S=3，S=4 的稀疏参数向量个数下验证基于稀疏图码的混合着色算法，重构信号所需要的测量维度和时间复杂度。图4 展示了在100 次实验下不同信号长度成功重构信号所需要的测量值对的数量。图5 中，展示了在100 次实验下不同信号长度成功重构信号所需要的平均运行时间。从测量维度和时间复杂度来看，成功重构信号时，两者均与信号的长度N无关。因此，该算法仅需要Θ(K)的测量维度和时间复杂度就可以成功进行混合稀疏线性回归的参数估计。

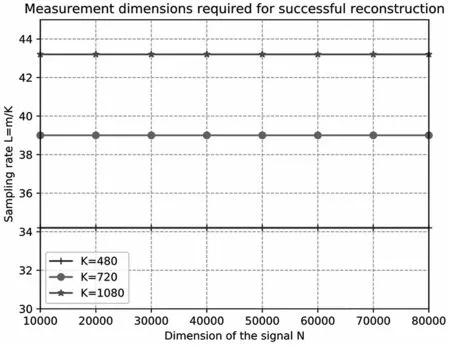
图4 成功重构信号所需测量维度

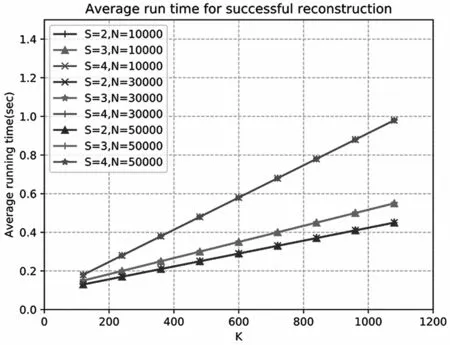
图5 成功重构信号所需时间复杂度

3 结语

在信号处理的重构稀疏信号领域，本文以构造实用、高效的查询矩阵以及设计低复杂度的稀疏信号回归重构算法为出发点，针对混合稀疏线性回归的参数估计问题，利用现代编码理论和稀疏线性回归系统之间的关系，提出一种基于稀疏图码思想来构造查询矩阵并进行参数估计的逐步迭代分离算法，该算法框架主要包括总和校验、比值测试和迭代剥离三个部分。然后，根据所提出的理论方法进行仿真实验，分别从测量维度、算法复杂度以及测量性能三个方面来验证理论设计。最终得出对于固定个数的稀疏参数向量，逐步迭代分离算法可以达到顺序最优样本和时间复杂度Θ(K)。在后续的工作中将对含有噪声的混合稀疏线性回归参数估计问题设计具有鲁棒性的快速重构算法。