关注儿童“数学现实”,构建“以生为本”的数学课堂——以北师大版数学五年级上册“组合图形的面积”为例
福建泉州市实验小学 王明滨
所谓儿童的数学现实,是指儿童的生活经验、认知经验、思维方式、解题策略以及有关的数学知识结构。只有关注儿童的数学现实,才能准确把握学情,抓住学生认知的起点,构建以生为本的数学课堂。本文以北师大版数学五年级上册“组合图形的面积”一课为例,谈谈如何根据学生已有的数学现实,构建以生为本的数学课堂。
一、问卷访谈厘清学生现实的起点
这节课学生的数学现实是什么呢?光靠猜测和主观经验的判断是不够的。于是笔者采用了问卷和访谈的方式进行调查。五年级学生抽样52份,六年级学生抽样60份,这部分内容对于五年级学生来说是新知,属于前测阶段;对于六年级学生来说,则是旧知,属于后测。
问题:
想一想,算一算:
新买住房客厅平面图(如图1),需要买多少平方米的地板?
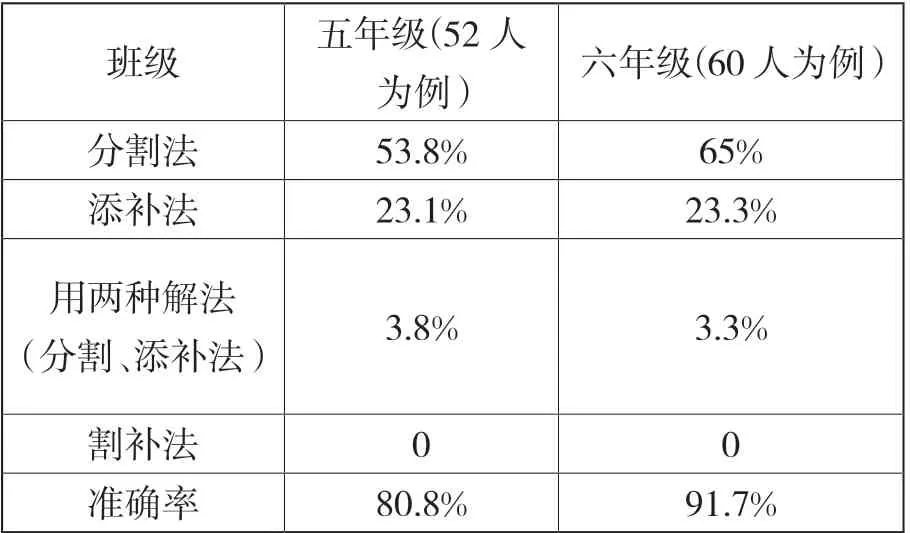
抽查的结果:
?
五年级学生所犯错误:①6人采用分割法,但数据提取错误;②2人采用添补法,不会计算;③1人计算周长;1人把所有线段相乘。六年级学生所犯错误:5人均采用分割法,都是数据提取错误。
1.学生偏爱“分割法”
分割法属于顺向思考,添补法属于逆向思考。割补法则是两种方法的综合运用,要求更高。分割法运用的是加法,只需要观察,所见即所得;添补法运用的是减法,需要将观察和想象相结合,对图形先进行扩充,再考虑整体和部分之间的联系。割补法,还涉及图形的旋转与平移、补特殊数据等。这些对学生来说是一大挑战,因此大部分学生偏爱“分割法”。
2.简化和优化的思想已初步形成
大部分学生把图形分割成两个图形,学生已经意识到图形分割越少,计算就越简单。同样的,在分割成两个图形的方法中,大部分学生选择分割成长方形和正方形,说明学生的优化意识已经初步形成。
3.计算分割后的图形时,数据提取容易出错
图形分割后,需要寻找新的数据,而新数据需要根据所提供的条件进行分析与判断,甚至需要重新计算才能得到,学生很容易在这里出错。
二、分析总结确定教学方向的依据
从前测中,我们发现只有10%的人不会计算这个组合图形的面积。那么,我们的教学仅仅只是满足这近百分之十的人要求吗?肯定不是!因此,这节课的教学目标应该体现以下两点:
1.灵活
灵活是指学生能根据组合图形的条件,灵活运用割补法正确计算其面积。例如:
图2是一个零件的横截面,计算它的面积。
根据题目所提供的数据,学生只能采用添补法,用大梯形的面积减去空白部分梯形的面积,如果生硬地把这个组合图形分割成三个小梯形,就会出现条件不足的情况。
2.多样
多样则是要求学生能感受解题策略、方法的多样性。
例如,如图3,计算中队旗的面积。(单位:cm)
这道题既能分割成两个梯形进行计算,也能选择添补法,用长方形的面积减法一个三角形的面积;个别的学生甚至能运用割补法,转化成两个长方形后,再把面积相加。通过这节课的学习,学生要能感受到组合图形解题策略和方法的多样性。
三、动态生成构建以生为本的课堂
1.留白,提高学生思维的灵活性
试教时,为了让学生理解什么是组合图形,笔者一开始创设了如下情境(如图4):
让学生先通过分类,再进行比较,从而知道什么是组合图形。但是,在接下来探索客厅的面积时,学生却只呈现一种教学资源——分割法。为什么只有一种算法?其实,刚才出示的这些组合图形,具有很强的暗示性,已经把组合图形分割成一个个基本图形,学生受思维定式的影响,再也想不到其他的方法了。这种教学,用教师的方法替代了学生的思考,遮蔽了学生应有的视野,影响了学生思维的灵活性和深刻性。
因此,只要去掉组合图形内部的分割线,仅留下图形的轮廓,就可以避免以上的问题。如图5:
这种教学上的留白,能够动态生成不同的分割法和添补法,有效培养学生的空间想象能力,提高学生思维的灵活性。
2.比较,加深学生思考的深刻性
(1)估算引路
智慧老人准备给客厅铺上地板,请根据图6中的数据估一估,大约需要买多少平方米的地板?
(2)激发内需
思考:如果按照估计的数据去买,行吗?为什么?
学生通过讨论交流,明白:数据是估计出来的,按这些数据去买,可能多了,也可能少了,因此应该算出准确的面积才行。
(3)分类比较
展示学生四种计算方法:
方法1:分割成两个长方形(如图7)。
方法2:分割成一个长方形和一个正方形(如图8)。
方法3:分割成两个梯形(如图9)。
方法4:补上一个小正方形,使它成为一个大正方形(如图10)。
对以上四种方法,引导学生在分类中了解常用的组合图形面积的计算方法:分割法与添补法,同时感受转化的数学思想。
(4)算法优化
引导学生思考:为什么在分割时都把组合图形分成两个基本图形,为什么不分成三个、四个呢?在对比分析中,知道:分割的方法越简洁,计算起来越简单。同时指出:为了避免出现转化后的图形数据不足或提取数据出错的现象,要先观察图形中所提供的数据,再根据数据的特点灵活地转化成已学的图形。
在课堂生成的教学资源中,通过分类比较有利于学生观察不同分法的共性,区别出分割法与添补法的不同,同时感受到无论是分割还是添补,目的都是为了转化成已学过的图形。在这过程中,学生感受到的不只是方法,还有转化的数学思想,从而提高学生思维的深刻性。
3.取舍,关注动态生成的多样性
如果在教学的过程中没有出现“割补法”,教师是否要主动呈现?如果呈现,这是学生已达到的水平吗?为什么后测中,再也没有出现这种解法呢?首先,要用割补法,必须要具备数据的特殊性;其次,其操作的难度之大,注定只属于少数的人。如果课堂上自然生成,可以作为一种代表性资源展示;如果没有,教师应站在以学生和学习为中心的立场上,根据课堂生成灵活地展开教学。
总之,我们只有基于学生的数学现实,才能有的放矢地展开教学,让教师的教更好地服务于学生的学,从而真正构建以生为本的数学课堂。

