Indu-Bala乘积图的广义距离谱

卢鹏丽，刘文智

(兰州理工大学 计算机与通信学院，甘肃 兰州 730050)

距离谱理论[1]作为图论的一个重要研究方向，主要是通过图的各类矩阵(距离矩阵、距离拉普拉斯矩阵等)、特征根及其特征向量来研究图的拓扑结构和代数性质，广泛应用于计算机、复杂系统、化学、物理等学科中。关于距离谱和距离(无符号)拉普拉斯谱的研究现状如下：学者们已经计算得到了圈图[2]、路图[3]和完全二部图[4]等简单图的距离谱；Stevanovic和Indulal[5-6]得到了正则图的联图的距离谱，距离正则图和完全图的簇图的距离谱；Barik和Sahoo[7]得到了距离正则图和正则图的冠图的距离谱和距离(无符号)拉普拉斯谱；其他研究成果见文献[8-11]。在此基础上，本文计算了一类组合图的广义距离谱。通过简单地参数赋值，就可以得到距离(无符号)拉普拉斯谱，大大减少了距离矩阵相关谱的计算量。

1 基本概念和引理

2013年，Aouchiche和Hansen[1]受拉普拉斯矩阵和无符号拉普拉斯矩阵的启发，提出了图的距离拉普拉斯矩阵和距离无符号拉普拉斯矩阵的概念，并研究它们的谱。图G的传递矩阵记为Tr(G)，是对角线元素为Tr(vi)的n×n维对角矩阵。图G的距离拉普拉斯矩阵和距离无符号拉普拉斯矩阵分别记为L(G)=Tr(G)-D(G)和Q(G)=Tr(G)+D(G)，相应的特征值分别为λ1L(G)≥λ2L(G)≥…≥λnL(G)=0，λ1Q(G)≥λ2Q(G)≥…≥λnQ(G)，相应的特征值及其重数所构成的集合称为图G的距离拉普拉斯谱和距离无符号拉普拉斯谱，记为L-谱和Q-谱。

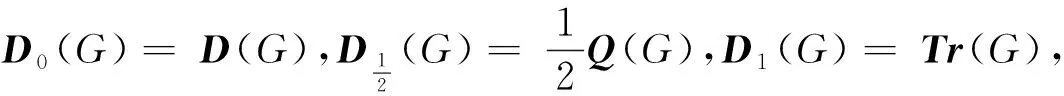
受到Ligong Wang[12]和G. Indulal[13]论文的启发。文献[12]中，图Kn,n+1≡Kn+1,n是将Kn,n+1复制2次，然后将2个复制图中的n+1个对应顶点相连接，其中Kn,n+1是完全二部图，作者证明了Kn,n+1≡Kn+1,n是邻接整谱图。文献[13]中，作者将图Kn,n+1≡Kn+1,n一般化到图G1G2，是将G1和G2的联图复制2次，然后将2个复制图中G2的对应顶点相连接所得到的图，计算了其距离谱。明显地，图Kn,n+1≡Kn+1,n是图G1G2的一种特殊图在此基础上计算了G1G2的广义距离谱，进而求得距离(无符号)拉普拉斯谱。

引理1[15]设图G的距离拉普拉斯谱为{λ1L(G)≥λ2L(G)≥…≥λnL(G)=0}，平均传递为t(G)，则图G的距离拉普拉斯谱能量定义为:

引理2[15]设图G的距离无符号拉普拉斯谱为{λ1Q(G)≥λ2Q(G)≥…≥λnQ(G)}，平均传递为t(G)，则图G的距离无符号拉普拉斯谱能量定义为:

2 图G1G2的广义距离谱

定理1设图Gi是有ni个顶点的ri-正则图，其邻接矩阵Ai对应的邻接谱为{ri,λi2,λi3,…,λini}，i=1,2。那么图G1G2的广义距离谱为:

1)(5n1+3n2-r1+λ1j)α-λ1j-2，j=2,3,…,n1,每一个重数为2；

2)(3n1+5n2-2r2+2λ2j)α-2λ2j-4，j=2,3,…,n2；

3)(3n1+5n2-2r2-4)α，重数为n2-1；

4)方程组的解

其中，B*=(3n1+3n2)α+2n1-r1-2，C*=(3n1+3n2-r2-2)α+2n2-r2-2。

证明：对图G1G2的顶点进行适当编号，图G1G2的距离矩阵可以表示为:

根据距离矩阵，得到图G1G2中每个顶点的传递Tr(u)=5n1+3n2-r1-2，u∈V(G1)；Tr(v)=3n1+5n2-2r2-4，v∈V(G2)。因此，图G1G2的广义距离矩阵可以表示为:

式中：M*=(3n1+5n2-2r2-4)αI+(1-α)(2J-2I-A2);N*=(5n1+3n2-r1-2)αI+(1-α)(2J-2I-A1);J是全1矩阵;I是单位矩阵。

因为Gi是ri-正则图，所以Ai的特征值ri所对应的特征向量是全1向量1，其他特征向量都和1正交。设Ai的特征值λi≠ri所对应的特征向量为Xi，则AiXi=λiXi，1TXi=0，i=1,2。

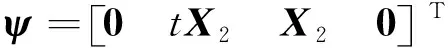
求解方程组可得：

μ=(3n1+5n2-2r2+2λ2j)α-2λ2j-4，j=2,3,…,n2；μ=(3n1+5n2-2r2-4)α，重数为n2-1。

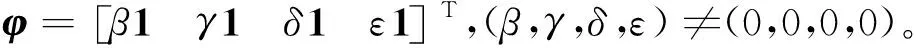
设σ是矩阵Dα(G1G2)的特征向量φ所对应的特征值，根据Dα(G1G2)φ=σφ和Ai1=ri1，i=1,2可得:

式中:B*=(3n1+3n2)α+2n1-r1-2，C*=(3n1+3n2-r2-2)α+2n2-r2-2。

假设β=0代入上面方程组，化简得γ=δ=ε=0，矛盾。因此，不失一般性，假设α=1求解上面方程组可得定理中的第(4)部分，证毕。

3 图G1G2的距离拉普拉斯谱

定理2设图Gi是有ni个顶点的ri-正则图，其邻接矩阵Ai对应的邻接谱为{ri,λi2,λi3,…,λini}，i=1,2。那么图G1G2的距离拉普拉斯谱为:

1)5n1+3n2-r1+λ1j，j=2,3,…,n1,每一个重数为2；

2)3n1+5n2-2r2+2λ2j，j=2,3,…,n2；

3)3n1+5n2-2r2-4，重数为n2-1；

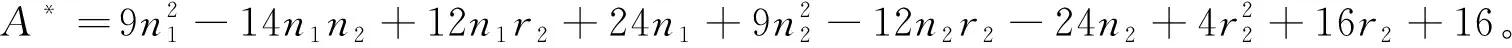
证明：已知Dα(G)-Dβ(G)=(α-β)L(G)，取α=1，β=0得L(G1G2)=D1(G1G2)-D0(G1G2)，则由定理1可得定理2，证毕。

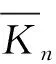
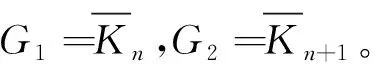
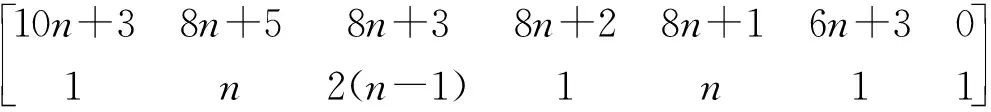
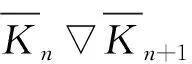
4 图G1G2的距离无符号拉普拉斯谱

定理3设图Gi是有ni个顶点的ri-正则图，其邻接矩阵Ai对应的邻接谱为{ri,λi2,λi3,…,λini}，i=1,2。那么图G1G2的距离无符号拉普拉斯谱为:

1)5n1+3n2-r1-λ1j-4，j=2,3,…,n1, 每一个重数为2；

2)3n1+5n2-2r2-2λ2j-8，j=2,3,…,n2；

3)3n1+5n2-2r2-4，重数为n2-1；

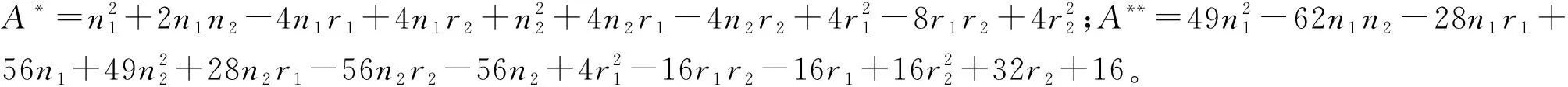
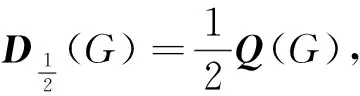
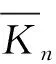
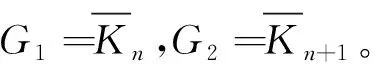
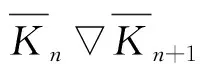
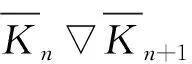
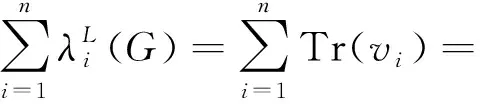
5 结论

1)主要研究了2个正则图经过Indu-Bala乘积这一图操作之后所形成的合成图的广义距离谱，揭示了合成图的广义距离谱、距离(无符号)拉普拉斯谱与原图的邻接谱之间的关系，不仅拓宽了组合图广义距离谱的研究范围，而且大大减少了距离(无符号)拉普拉斯谱的计算量；

2)得到了一类特殊的距离(无符号)拉普拉斯整谱图；

3)得到了特殊图的距离(无符号)拉普拉斯谱能量公式。