标记关联的多声呐多目标航迹融合方法

生雪莉，陈洋，郭龙祥，郝豪言，周媛媛，殷敬伟

(1.哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨 150001； 2.海洋信息获取与安全工信部重点实验室(哈尔滨工程大学)，工业和信息化部，黑龙江 哈尔滨 150001； 3.哈尔滨工程大学 水声工程学院，黑龙江 哈尔滨 150001)

水声目标跟踪一直都是声呐领域中重要研究的课题。近几十年来，随着海洋船舶技术和舰船降噪技术的快速发展，以及人类海洋活动的频繁，目标输入信号的信噪比不断下降，导致水声目标跟踪技术朝着分布式融合方向进行了发展[1]。目前，传统的目标跟踪算法，如多假设跟踪(multiple hypotheses tracking, MHT)算法、联合概率数据关联(joint probabilistic data association, JPDA)等算法通常需要进行复杂的关联计算，因此当量测个数较多时，算法的计算复杂度大幅增加，严重时可能无法进行计算[2-3]。然而，基于RFS理论的概率假设密度(probability hypothesis density, PHD)滤波器由于不需要进行关联计算，因此计算效率大幅提高。例如高斯混合概率假设密度(gaussian mixture probability hypothesis density, GMPHD)滤波器[4]，其计算复杂度与量测个数和次数均呈线性关系[5]。因此，这类方法在假目标干扰严重的场景中解决水声目标探测问题具有重要的应用价值[6]。例如，洛马公司的反潜多目标跟踪识别系统和海军研究办公室的被动声呐反潜信息融合和目标识别系统[7]。但是，这种方法也存在一个明显的缺点，那就是只能生成点迹估计，而无法提供目标的航迹信息，这给后续的航迹融合、航迹管理等工作带来了困难。

在解决PHD算法航迹问题的方法中，主流的做法有2个方向[8]。一类是通过关联算法来解决PHD的目标航迹生成问题。文献[9-10]利用数据关联算法对序贯蒙特卡洛概率假设密度(sequential monte carlo probability hypothesis density, SMCPHD)滤波器进行改进，解决了SMCPHD滤波器的目标航迹生成问题。文献[11]则对比了SMCPHD和MHT算法性能，并发现SMCPHD生成的航迹相比传统MHT算法生成的航迹效果更好。Clark还对SMCPHD和GMPHD跟踪滤波器的航迹生成问题给出了多种解决方案[12-13]，并成功解决了基于声呐图像数据的多目标跟踪问题[14]。

另一类是给PHD滤波器的目标状态增加一个标记，通过标记信息确定目标的航迹。例如文献[16]通过增加一个额外的标记来区分不同的航迹，解决了航迹生成问题。文献[17]不仅利用标记信息解决了航迹问题，还提高了PHD滤波器剪枝算法的效率。文献[18]则利用高斯项的标记集进行标记的假设关联，并采用匈牙利算法寻求最优的假设关系，为GMPHD滤波器提供一个更加稳定的目标航迹。文献[19]则对GMPHD滤波器中的高斯项进行标记，并利用树状结构传递这些标记，完成目标航迹标记的更新，解决航迹生成问题。此外，Karl[20]和Han[21]等则在扩展目标的航迹问题进行深入研究，并提出了相应的解决方法。

借鉴上述方法经验，本文以GMPHD滤波器为基础，通过将数据关联方法与标记法相结合，提出了一种适用于多声呐多目标航迹的生成融合方法，旨在解决单传感器受时空非均匀传播问题，降低环境噪声的影响。此外，本文还利用标记信息构建了一种简易的延时滤波器，解决了PHD滤波器估计遗漏的假目标问题。

1 PHD理论

在目标跟踪问题中，贝叶斯滤波方法是当今最为常用的方法。令fk|k-1(xk|xk-1)表示状态x从k-1时刻到k时刻的马尔可夫转移密度，gk(·|·)表示似然函数，pk表示k时刻的后验概率密度，z表示量测，那么根据贝叶斯滤波理论有:

(1)

(2)

将其推广到在多目标的探测环境下，首先根据RFS理论，可以将k时刻的目标状态和传感器的量测分别建立为一个随机有限集，即：

Xk={xk,1,xk,2,…,xk,N(k)}∈F(χ)

(3)

Zk={zk,2,zk,2,…,zk,M(k)}∈F(Z)

(4)

式中：x表示目标状态；z表示传感器的量测；F(Z)和F(χ)为单目标量测z和状态x的全部有限子集的集合。

考虑到k时刻的目标状态可能有3种：新生、衍生以及灭亡，那么目标状态集Xk还可以表示为：

(5)

式中：Sk|k-1、Bk|k-1和Γk分别表示为从k-1时刻存活、衍生到k时刻的目标和k时刻新生目标。

同时，在量测过程中还可能伴随漏检、错误量测以及干扰的影响，则k时刻的量测集可表示为：

(6)

式中：Kk和Θk分别表示为第k时刻的错误量测和干扰。

因此，可将单目标的贝叶斯滤波推广到多目标随机有限集的贝叶斯滤波，即:

(7)

(8)

式中μs为F(X)的一个参考指标。

最后，通过MMSE(minimum mean squared error)或MAP(maximum a posteriori)准则便可估计出目标k时刻的状态。可见，PHD滤波器避免了传统跟踪算法中的关联过程，提高了计算性能，但其递推公式却存在解析解难求的问题。为此，Ba-Ngu Vo提出了采用粒子近似的SMCPHD滤波器和采用高斯混合近似的GMPHD滤波器。本文假设系统服从高斯模型，因此选用计算效率更高的GMPHD滤波器作为本文的核心滤波器，其具体实现过程可参见文献[4]。

2 标记关联的多声呐航迹融合

2.1 分布式多声呐数据融合结构

如图1所示，在分布式多传感器融合方法框架下，本文首先利用GMPHD滤波器为每个声呐的量测进行独立滤波，得到局部估计(点迹)。其次，为局部估计增加一个特殊的标记，并利用关联算法确定局部估计间的关联关系，完成标记更新并形成局部航迹。再次，利用关联算法确定不同声呐局部估计之间的关联关系，并利用标记关联关系优化关联计算过程以及对错误标记进行纠错。最后，根据关联关系，通过多传感器融合算法完成航迹融合，得到融合后的全局航迹。此外，利用全局航迹中的标记信息，本文还给出了一种简易的延时滤波器，可以滤掉存活时间较短的假目标航迹，令全局航迹估计结果更加可靠。

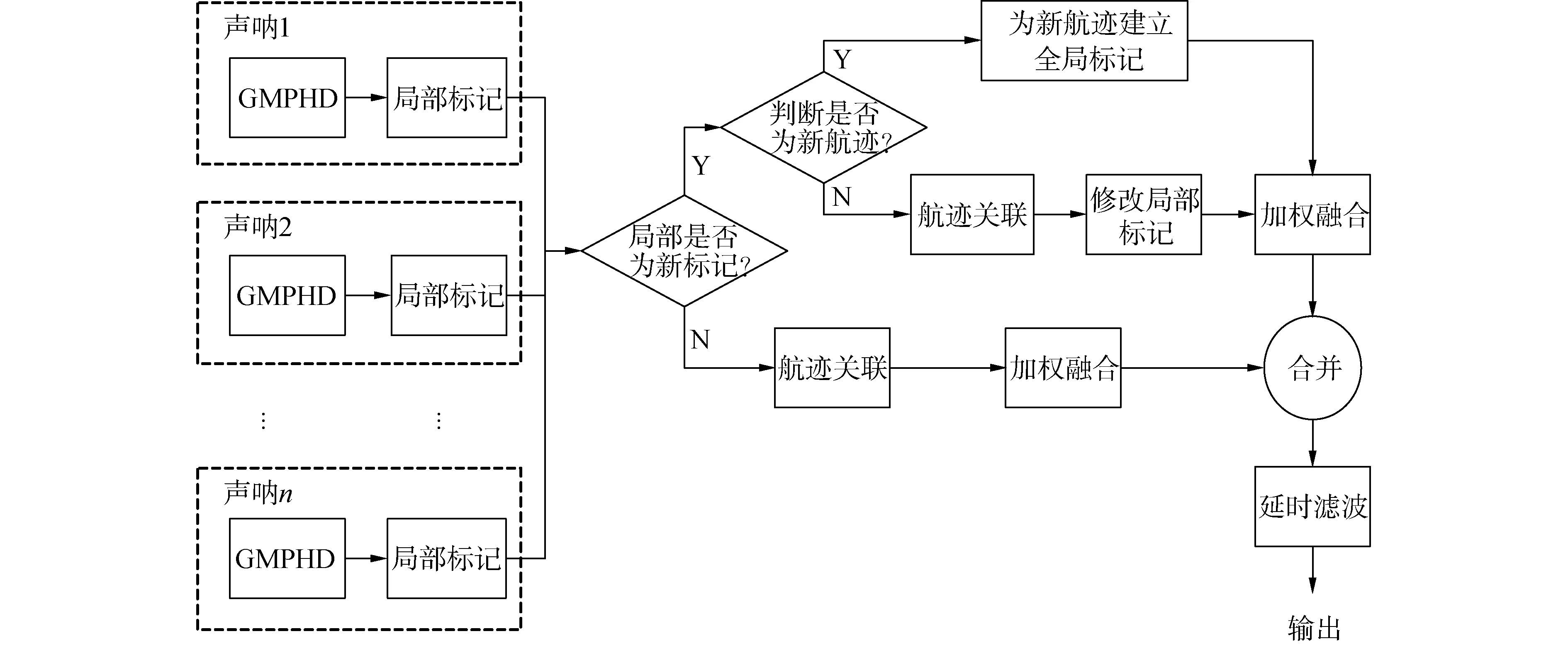
图1 分布式多声呐数据融合结构Fig.1 Distributed multi-sonar data fusion structure diagram

2.2 基于标记的航迹关联方法

在本文中，主要选用一种基于马氏距离的最近领域法(nearest neighbor，NN)来解决数据关联问题，即确定点迹与点迹、点迹与航迹以及航迹之间的关联关系[22]。若用x1和x2表示待关联的2个状态，p1和p2表示其对应的误差协方差矩阵，则可以计算出2个状态之间的马氏距离α：

α=(x1-x2)T(p1+p2)(x1-x2)

(9)

那么，通过设立门限Tα，当α小于门限Tα时，则认为2个状态是相互关联的，其中α值越小，2个状态的关联程度越高。

2.2.1 标记的局部声呐航迹关联

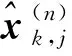
(10)

(11)

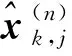
2.2.2 标记的全局多声呐航迹关联

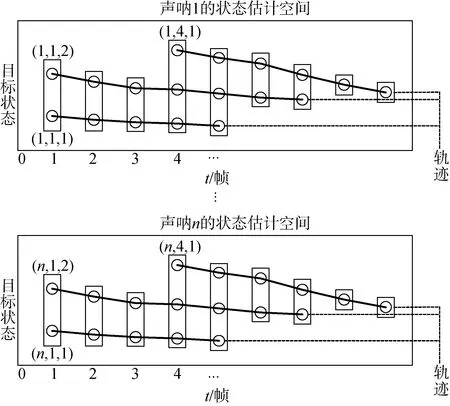
图2 分布式多声呐航迹关联示意Fig.2 Distributed multi-sonar track association diagram

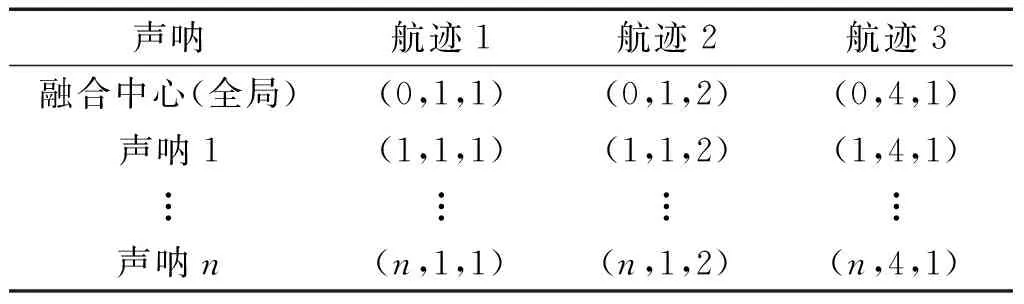
表1 全局关联表AHTable 1 Globally associated table AH

可以看出，利用AH表可以优化关联计算问题，提高关联计算效率，即通过“行”排列便可找出同一声呐(包含融合中心)中各个航迹的标记；通过“列”排列便可找出同一航迹对应不同声呐中的局部航迹标记的关联关系。

再次，若局部估计为一个新目标的标记(即AH表中未确定该标记与全局标记间的关联关系)，则可以利用式(9)～(11)，采用多次外推的方法确定该新生目标的局部标记与全局标记间的关联关系。若无法找到对应的关联关系，则认为系统检测到一个新生的目标航迹，并对AH表的记录进行更新;否则，则根据AH表进行标记纠正。

最后，由于在全局航迹中，其标记的第2项参数已经记录了多声呐第1次检测到该目标航迹的起始时刻，因此，仅需要为该全局航迹添加一个结束时刻的标记，即可实现对该航迹存活时间的记录，即每当存在该航迹时，则对该航迹的结束时刻进行更新。

2.3 基于标记的多声呐数据融合和延时滤波器

在多传感器数据融合方法中，简单凸组合融合算法是一种容易工程实现，且当两传感器局部估计误差不相关时，可以得到最优估计的融合方法[23]。但是，该方法并没有考虑声呐漏检等问题。因此，本文主要根据AH表中的关联关系，将加权融合策略和简单凸组合融合方法相结合，完成多声呐的数据融合，得到全局航迹估计。

2.3.1 简单凸组合融合技术

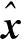
(12)

将式(12)推广到多声呐(n>2)的情况时，则有：

(13)

2.3.2 加权融合策略

为了实现整个探测系统具有最大的检测能力，本文的加权融合策略为：若多个声呐的局部估计可以相互关联且关联程度最小时，则利用简单凸组合融合方法进行数据融合，得到全局航迹估计；否则，由于无法判断该目标状态是否为其他声呐漏检的目标，因此本文将所有没有关联上(α>Tα)的局部航迹也保留作为全局航迹估计。需要说明的是，这个加权融合策略可能会导致全局航迹中存在假目标航迹，因此需要进行后续的滤波处理。

2.3.3 基于标记的延时滤波器

通常，真实目标的航迹应该是相对连续的，而干扰的假目标的航迹是相对孤立的。因此，本文借助全局航迹的标记信息，通过计算每个全局航迹的存活时间和被检测到的次数，便可以比较为容易地滤除掉假目标。例如，可以统计第k到第k-s帧内，同一目标航迹被检测到的次数。若统计的次数少于aPd·s，则判定为假目标，直接滤除即可，其中a为常数，Pd为检测概率。

3 数值仿真

本文将借助OSPA(optimal sub-patten assignment)指标对本算法性能进行检验。根据OSPA的定义，若令X={x1,x2,…,xn}和G={g1,g2,…,gm}分别表示估计出的目标状态集和目标状态真值集。其中，x和g分别代表目标状态和真值，那么，OSPA指标可以被定义为[24]：

(14)

式中:dc(x,x′)=min{c,d(x,x′)}为相关程度的截止距离度量;c为关联截至半径;p为一个无量纲实数。

3.1 常规观测场景

在[-1 000 m,1 000 m]×[-1 000 m,1 000 m]的监视场景下，假设2声呐均可以对该范围所有的出现的目标进行探测。其检测概率为Pd=0.9。目标状态用xk=[px,kpy,kvx,kvy,k]T来表示，其中(px,k,py,k)为目标在k时刻的位置状态，(vx,k,vy,k)为对应的矢量速度。在连续观测100帧数据的试验条件下，共模拟3个匀速直线运动的目标。其中，目标1在第1帧位置(-900,-900)出现，在第80帧终止在位置(600,600)处；目标2在第1帧位置(-900,0)出现，在第100帧终止在位置(500,-900)处；目标3在第60帧以速度[-20;0](m/s)在位置(300,0)处进行移动。算法考察近5帧的历史数据，即s=5。

假设在监视范围内，共模拟2个声呐进行联合探测。其中，每个声呐的探测过程都是相互独立的，并且声呐的量测数据中每帧最多包含50个假目标干扰，且假目标位置服从均匀分布。马尔可夫转移状态矩阵F、过程噪声协方差矩阵Q和量测噪声协方差矩阵R分别为：

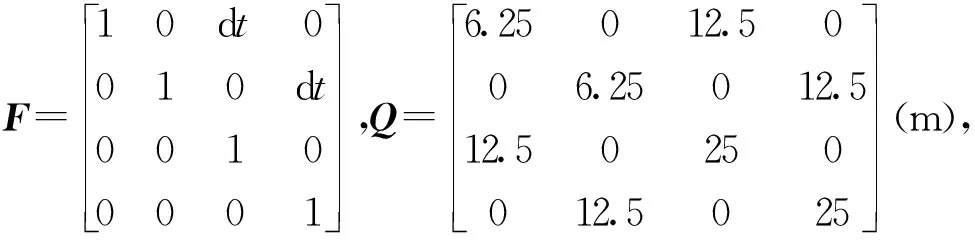
R=diag(100,100,100,100)(m2)。

式中dt=1 s为观测周期。

如图3所示为本次仿真试验结果。可以看出，图3(a)和(b)体现了GMPHD具有良好的目标跟踪滤波能力；图3(c)的仿真结果不仅证明了本方法能够实现多声呐的数据融合，得到全局估计结果，还很好地形成了目标航迹；图3(d)的OSPA分析结果则表明了全局估计结果相比任意局部声呐的估计跟踪结果更加精确、稳定(均值更小、方差更小)。

图3 常规观测场景下的仿真结果Fig.3 Simulation results under conventional observation

3.2 间断观测场景

在3.1节的仿真场景下，本文还考察了一种间断的观测场景。其中，假设声呐1从第20帧～第70帧受到海洋信道等因素影响，导致该声呐无法探测到目标1，形成对目标1的间断观测，其仿真结果如图4所示。

对比图4(a)和(c)可以看出，虽然声呐1在一段时间内都无法探测到目标1，但是当该声呐再次探测到目标1时，理论上会判定为一个新目标的航迹(长时间未检测到该目标)。但是，由于本算法在航迹生成融合过程中，借助AH表对航迹的标记进行了纠错，因此可以得到一个正确的局部航迹，如图中4(c)航迹1所示。从图4(b)、(e)和(f)中可以发现，当2个声呐至少有一个声呐可以探测到目标时，本方法便可以得到一个相对稳定、连续的目标航迹。

3.3 延时滤波器

由于本文的加权融合策略可能会导致全局航迹中存在比较明显的假目标航迹。为此，在本节中主要通过仿真验证延时滤波器的作用。在上一节仿真条件下，延时滤波器的检测常数a=0.5。其仿真结果如图5所示。

在图5(a)中，声呐1在(-450,-150)处附近产生了一个明显的错误估计。由于本文的加权融合策略，导致了全局航迹估计中产生了对应的错误航迹(如图5(c)所示)。但是，利用本文的延时滤波器，可以滤掉将这种存活时间较短的假目标航迹，降低了加权融合策略所导致的全局估计中存在假目标的可能性，进一步保证了算法估计的正确性。当然，也可以利用MHT或JPDA方法进行二次滤波来滤掉这种存活时间比较短的假目标，但是，这种做法显然没有统计航迹标记个数简单、易实现。

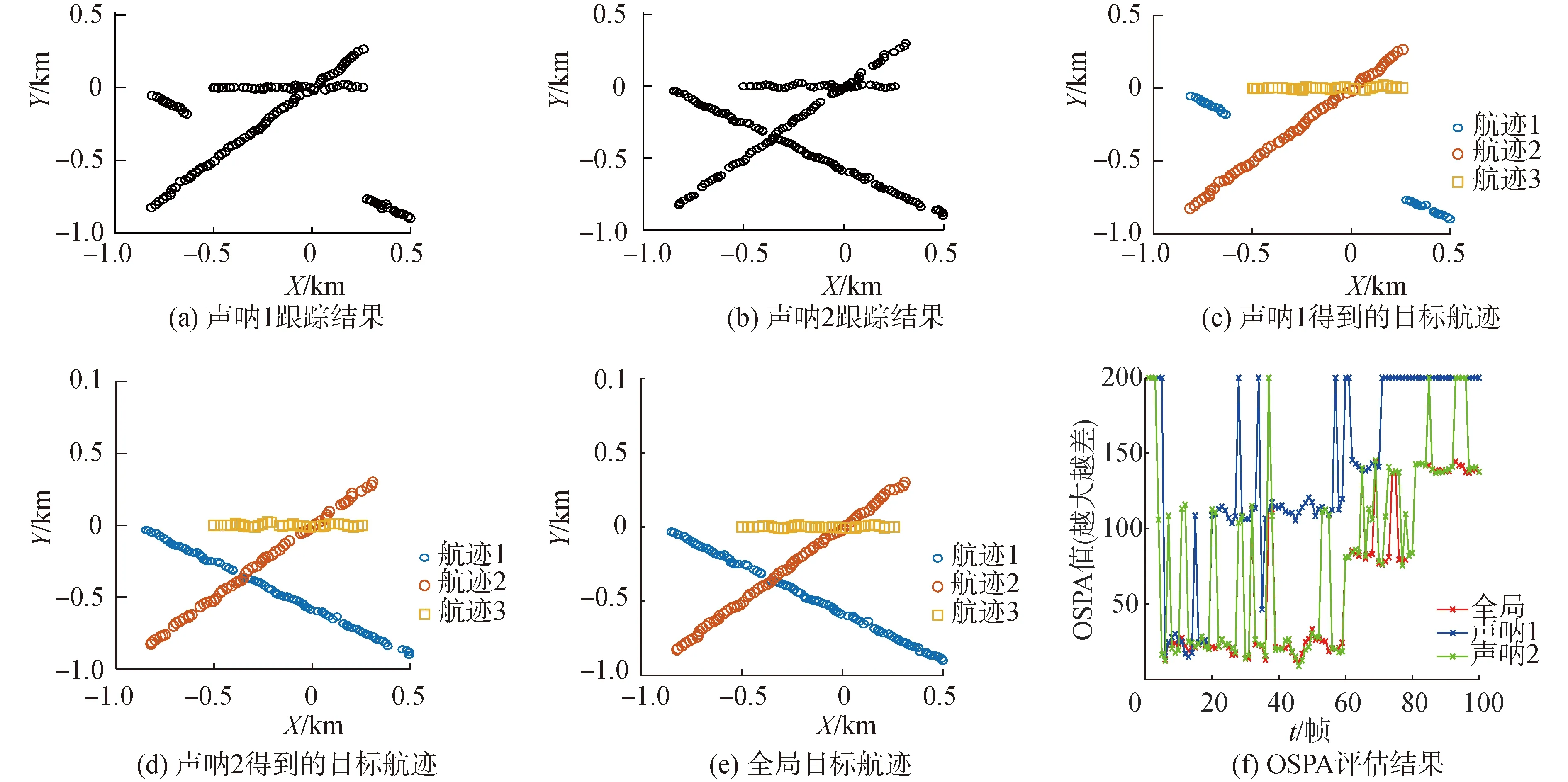
图4 间断观测场景下的仿真结果Fig.4 Simulation results under intermittent observation scene

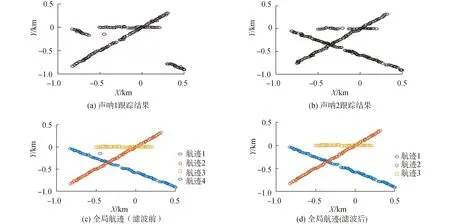
图5 延时滤波仿真结果Fig.5 Simulation results of delay filtering

4 结论

1)即使某个声呐无法对目标进行连续观测，也可以正确地确定该目标航迹信息。

2)基于标记的延时滤波器不仅可以进一步滤除局部声呐中的假目标干扰，还具有工程易实现等优点。在OSPA评估算法的帮助下，仿真试验从常规观测和间断观测2个场景检验了该方法的性能，证明了该方法具有形成准确、连续目标航迹的能力。此外，延时滤波器的仿真也说明了这种滤波器能够有效地滤除存活时间较短的假目标干扰。