有压输沙管道脉动压强特性试验研究

李 岩，张金良，白玉川，万占伟，罗秋实，胡文励

（1.天津大学 河流海岸工程泥沙研究所，天津 300072；2.黄河勘测规划设计有限公司，河南 郑州 450003）

1 研究背景

黄河是一条多沙河流，自西向东流经九省（自治区），干流全长5464 km，流域面积79.5万km2，进入下游河道泥沙多年平均为16亿t，平均含沙量高达35 kg/m3[1]。为了促进黄河流域生态保护和高质量发展，对黄河的水沙资源进行重配置，确保实现水沙资源的有效利用。管道输送是实现黄河水沙资源重分配重要工程措施之一，因其造价低廉，易安装，对环境危害小等优点被广泛用在黄河流域，如上游水库泄洪排沙，沿黄河道引水引沙与下游滩区淤沙等。高含沙管道输送对于恢复水库库容，维持河槽稳定，提高滩区土壤肥力，改善滩区生态环境具有重要的作用。

图1 年均含沙量与高含沙水流输沙比例关系

张金良[2]通过统计黄河流域30余条重要支流，绘制出年均含沙量与高含沙水流输沙比例的关系，提出了高（年均含沙量10～100 kg/m3）、超高（年均含沙量100～200 kg/m3）、特高（年均含沙量200 kg/m3以上）含沙量河流分级标准，如图1所示。高含沙水流因细颗粒含量的增多改变了流体性质，其输沙特性和紊动特性均发生质的变化，高含沙运动所消耗的能量主要来自于水流紊动动能，而泥沙的存在一定程度上抑制了紊动的发展，紊动强度随着含沙浓度的增加而逐渐减小[3-4]。壁压脉动是湍流脉动的一种特殊表现形式，是湍流拟序结构对边壁作用的反映[5-6]，而泥沙颗粒的运动也反映了湍流动力的特征，白玉川等[7]通过分析明渠沙纹床面湍流结构和特点，对脉动强度、湍流动能等特征量进行了计算，后来白玉川等[8]开展弯道水流紊动特性试验，研究了弯道水流紊动的脉动强度。随着河流流域水库的修建，对泄水和消能建筑物脉动压强特性研究[9-18]进入快速发展阶段，而天津大学在很早之前就对水流运动引起的脉动压强进行过深入的研究，从早期赵耀楠等[19]研究高坝下游水流脉动压力沿缝隙峰传播，到后来高学平等[20]按照重力相似准则设计模型模拟水电站有压管道的水击现象等。不过以往的研究多是基于清水工况，没有考虑泥沙因素的影响，泥沙存在会导致水流运动不稳定引起脉动压强变化，而高含沙、超高含沙、特高含沙的出现会诱发建筑物振动、过机破坏，影响泄洪洞、排沙洞、输水隧洞等稳定性与运行安全。

本试验基于以往的研究基础，按照高、超高、特高含沙划分标准，构建管道输沙模型，通过改变不同含沙浓度，研究不同工况下管道流量和含沙浓度变化对壁面脉动压强特性的影响，进一步剖析泥沙运动引起的管道脉动复杂行为及其背后的物理特性，为泄洪输沙隧洞（管道）等水工建筑的稳定安全运行提供技术参考。

2 试验概况

2.1 试验系统试验在总长度约30 m，直径80 mm 的封闭管道进行，试验装置布置如图2所示。管道水平布设，离地面约30 cm，其中试验段采用长12 m 的有机玻璃管，沿管壁布设一排压强传感器探头，测点编号从1#—6#，间隔2 m，采样频率为125 Hz，采样间隔0.008 s，采样点数2000。管路与离心泵之间采用0.5 m 的软管相连，在进出口附近设置阀门，用于流量控制和管道含沙浓度测量，并配置电磁流量计监测管中流量，辅以体积法加以检验。

图2 模型试验系统

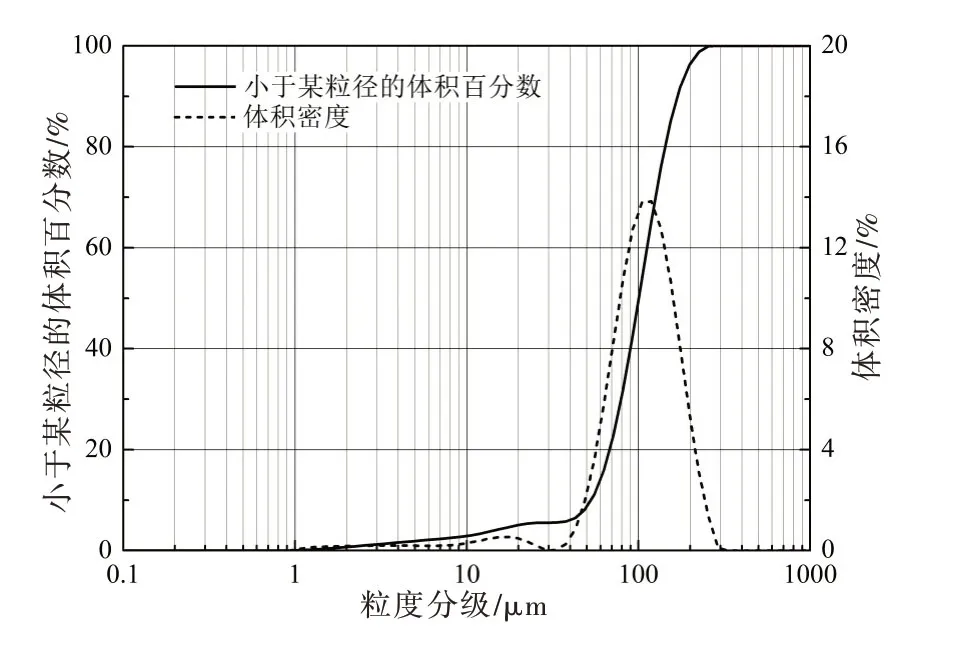
图3 泥沙粒度分析

试验选用山东济阳滩区的黄河细沙作为试验对象，沙样密度约为2650 kg/m3，采用超高速智能粒度分析仪（Ultra-high speed intelligent particle size Analyzer）对泥沙样品进行粒度分析，分析结果如表1所列，粒径级配曲线和不同大小的颗粒体积密度分布如图3所示。从表1和图3结果可知，该泥沙粒径分布范围较窄，非均匀程度泥沙粒径组成比较均匀，中值粒径d50=107μm，均值粒径=112 μm。

表1 泥沙粒径级配

2.2 试验工况为研究水平管道中流速变化、含沙浓度的差异对脉动压强的影响，在控制流量为10（±0.91）、15（±0.28）、20（±0.28）、30（±0.99）m3/h条件下配置不同含沙浓度（Cv=0～21.75%）等24组工况进行试验。在试验过程中，管中泥沙会对电磁流量计产生一定的影响，通过阀门很难调整到完全相同的流量，管中测量含沙浓度跟水池含沙浓度有一定的误差，因此本试验采用的含沙浓度为管中实测数据，为了保证测量数据是在管中含沙浓度相对稳定情况下获得，采取以下措施：（1）水池中装有螺旋搅拌器，不间断搅拌浑水，确保泥沙能够充分进入循环管道；（2）含沙水流进入管路运行一段时间后，在管道进口和出口位置通过阀门接取管中浑水，量测含沙浓度并进行对比，如果数值相差较大，重新进行该组试验；（3）在管道试验段中间位置设置一个皮托管，可通过分层取样法获得管道垂线泥沙浓度，与进出口测量的泥沙浓度进行对比。本试验详细工况如表2所列。

表2 试验工况

3 结果与讨论

3.1 时均压强试验过程中采集每组工况下壁面压强随时间的变化值，其瞬时值由两部分构成，即时均值和脉动值，表达式可写为′，脉动压强变化是一个随机过程，图4是1#位置在清水工况下（Cv=0%）流量分别为10.06 m3/h和30.45 m3/h 对应的实测瞬时压强波形图。

水平管道输沙的主要驱动力是压力，前后压差的存在驱动管中泥沙向前输移，有压管道输沙过程中，时均值变化是反映水沙运动引起管壁压强变化的重要参数。图5是在流量10（±0.91）、15（±0.28）、20（±0.28）、30（±0.99）m3/h条件下不同含沙浓度引起的沿程时均压强变化情况。横坐标以测点在试验段的相对位置（x为该测点距第一个测点的距离，L为试验段总长度），纵坐标为时均压强值（kPa）。由图5可知，管道输送清水或不同含沙浓度的浑水时，时均压强都是沿程逐渐降低的。

图4 实测瞬时压强波形（1#）

图5 沿程时均压强分布

图6为沿程时均压强降低幅度与含沙浓度关系，当输送清水时，随着流量增大，时均压强沿程下降幅度也越大；当输送含沙水流时，在相同流量条件下，沿程时均压强下降幅度随着含沙浓度的增加呈增大趋势，说明管道中泥沙浓度的增加需要消耗更多的能量。

图6 沿程时均压强降低幅度与含沙浓度关系

3.2 峰值压强在有压输沙管道中，因水流运动引起的脉动压强会对管道稳定性与安全性产生重要影响，其中峰值压强也是一个很重要的参数，管道输沙引起的峰值压强会在一瞬间对管壁造成强烈的压力，严重者会破坏管道结构，造成输沙受阻，峰值压强变化可作为管道稳定安全分析中一个参考参数。本次对采样时长内管道每个测点的最大瞬时峰值和脉动峰值压强进行了统计，分析含沙浓度变化对峰值压强的影响，如图7（a）所示，从图7（a）可知，最大瞬时峰值压强的变化总趋势是随着管中含沙浓度的增加呈逐渐增大的。图7（b）最大脉动峰值压强与含沙浓度的关系，（1）当流量为10 m3/h 左右时，含沙浓度小于Cv=17%情况下，脉动峰值压强受含沙浓度影响较弱，含沙浓度Cv大于17%后，脉动峰值压强呈增大趋势。随着含沙浓度的增加，管底沉积厚度也逐渐增加，减小了管道过流面积，在保持流量不变的情况下，管道上部区域流速会有所增大，水流脉动流速增强，引起的管顶脉动峰值压强随之变大。（2）当流量为20 m3/h 左右时，脉动峰值压强随着含沙浓度增加呈增大趋势。该流量条件下管道水流动力较强，由于泥沙颗粒自重作用，浓度呈上小下大分布，下部区域泥沙浓度大，最大流速会向上部区域偏移，导致上部水流脉动增强，引起的管顶脉动压强增大。（3）当流量为30 m3/h 左右时，管道水动力条件明显增大，管道水流垂向脉动很大，细泥沙颗粒较难沉降，脉动峰值压强随泥沙浓度增加变化较弱。当含沙浓度增大到一定程度后，垂线泥沙浓度从上小下大型趋向均匀分布，泥沙颗粒之间间距减小，抑制了水流紊动发展，垂线流速分布较均匀，相较于流量为20 m3/h脉动峰值压强是减小的。

图7 瞬时峰值压强、脉动峰值压强与含沙浓度关系

3.3 压强脉动强度和相对脉动强度在紊流流场中，任一点的瞬时压强表示为时均值与脉动值之和，即压强均值的大小用表示，脉动压强的均方根可以表示压强脉动强度，而压强相对脉动强度为表征流体紊动程度强弱的另一个指标。在流量分别为10、20、30 m3/h条件下，不同含沙浓度引起的压强脉动强度和相对脉动强度如图8所示。

图8 压强脉动强度、相对脉动强度与含沙浓度关系

图8（a）为压强脉动强度与含沙浓度关系，在管道中含沙浓度Cv小于20%情况下，管道顶部的压强脉动强度随流量增大而变大。（1）流量为10 m3/h 左右和20 m3/h 左右时，在含沙浓度Cv小于10%情况下，脉动强度受含沙浓度影响较弱；含沙浓度Cv大于10%后，脉动强度随含沙浓度增加呈增大趋势。在浓度相对较低情况下，管道垂线泥沙浓度呈上小下大分布，随着含沙浓度的增加，管底区域浓度逐渐增加甚至出现泥沙沉积或滑动底床现象，在保持流量不变的条件下，管道上部区域流速会有所增大，水流脉动流速增强，引起的管顶脉动压强随之变大。（2）当流量为30 m3/h 左右时，压强脉动强度随含沙浓度增加波动幅度较大，但总趋势呈缓慢下降的。流量为30 m3/h 左右时，管道水动力条件较强，细泥沙颗粒较难沉降，当含沙浓度逐渐增大到一定程度后，垂线泥沙浓度从上小下大型趋向均匀分布，泥沙颗粒之间间距减小，抑制了水流紊动发展，脉动强度呈下降趋势。

图8（b）为相对脉动强度与含沙浓度关系，由图可知相对脉动强度随着含沙浓度增加其总趋势是降低的。流量10 m3/h和流量30 m3/h 的相对脉动强度如表3和表4所列，当流量为10 m3/h时，1#位置的相对脉动强度：含沙浓度Cv=0%时为1.240，Cv=21.75%时降到0.957，减少了0.283；4#位置的相对脉动强度：含沙浓度Cv=0%时为0.979，Cv=21.75%时降到0.537，减少了0.442。当流量为30 m3/h时，1#位置的相对脉动强度：含沙浓度Cv=0%时为0.729，Cv=20.89%时为0.530，减少了0.199；4#位置的相对脉动强度：含沙浓度Cv=0%时为0.842，Cv=21.75%时为0.374，减少了0.468。综上所述，在均匀平顺管道中，脉动壁压强度主要受水流来流条件和含沙量的控制，泥沙的存在会对水流紊动起到一定程度的削弱，含沙浓度越高削弱效果越明显，相对脉动强度值越小。根据王尚毅有效悬浮功观点[21]，含沙浓度越高泥沙的悬浮功越大，水流提供的有效势能也随之增大，则总能量转化为紊动动能的分量就相应减少，因此高含沙浓度水流紊动比清水要弱。

表3 流量10（±0.91）m3/h 的相对脉动强度

表4 流量30（±0.99）m3/h 的相对脉动强度

3.4 脉动压强的概率密度壁面的脉动压强是一种随机荷载，平顺水流的脉动壁压，主要是由紊流边界层内区的垂直于边壁的脉动分速引起，目前一致的认识是：水流脉动压强振幅分布密度符合正态分布[22]。脉动压强的振幅分布密度按正态分布，可用下式计算：

式中：f（p）为概率密度函数；μ为期望；σ标准差；σ2为方差。μ是正态分布的位置参数，描述正态分布的集中趋势位置。σ也称为是正态分布的形状参数，σ越大，曲线越扁平，σ越小，曲线越瘦高。当μ=0；σ=1 时是为标准正态分布，记为N（0，1）。

标准差是任意随机变量偏离其平均值程度的一种度量，脉动压强的均方根又称为压强脉动强度，可以度量压强脉动的强弱，与水流的雷诺数Re密切相关。本次试验流量范围10～30 m3/h，雷诺数Re=4.4×104～1.3×105，从图9可以看出，雷诺数越高，压强脉动强度越大。

图9 压强脉动强度与水流雷诺数关系（清水工况）

通过计算获得管壁1#和4#两处位置脉动压强概率密度函数，如图10—图12所示，横坐标为脉动压强p′，图中表格数据分别为流量Q、期望值μ（即均值压强）、方差σ2。图10是清水工况（Cv=0%）流量分别为10、15、20、30 m3/h 时对应的脉动压强概率密度分布曲线，根据瞬时压强=脉动压强+时均压强，则脉动压强的均值为0，即脉动压强的概率密度分布为脉动压强均值接近于0 的正太分布。当流量为10.06 m3/h时，1#位置的方差为0.959和4#位置的方差1.066 均接近1，趋近于标准正太分布。同时发现，随着流量的减小，概率密度分布从矮胖型向瘦高型发展，脉动压强的振幅逐渐降低，向均值压强靠拢。图11和图12 是流量为10、30 m3/h条件下不同含沙浓度的脉动压强概率密度曲线，在相同流量情况下，随着含沙浓度的增大，方差σ2呈逐渐增大的趋势，脉动压强的概率密度分布从瘦高型逐渐发展成矮胖型，由原来的接近标准正态向一般正态分布发展。

为了进一步研究流量和含沙浓度的变化引起脉动压强概率密度分布规律，可以采用偏度（skew⁃ness）CS与峰度（kurtosis）CK检测脉动压强数据集是否符合正态分布。偏度系数CS是相对于平均值不对称程度的度量，能够判定脉动压强数据不对称程度及方向，而峰度系数CK是判定数据相对于正态分布而言是更陡峭还是平缓。

偏度和峰度计算公式如下所示：

图10 清水脉动压强概率密度分布

图11 不同含沙浓度下的脉动压强概率密度分布（1#）

图12 不同含沙浓度下的脉动压强概率密度分布（4#）

式中：p为瞬时值压强；为均值压强；σ为标准差。

本试验计算了流量为10 m3/h和30 m3/h条件下含沙浓度变化引起的压强偏度和峰度变化值，如表5和表6所示。

由计算结果可知，清水工况下的管壁脉动压强偏度值CS在-0.18～0.098之间，峰度值CK在-0.276～0.262之间，偏度值和峰度值接近于0，清水条件下的脉动压强概率密度分布接近正态分布。浑水工况下，流量为10 m3/h时，偏度值变化范围在-0.876～0.234之间，峰度值变化范围在-0.266～0.611之间；流量为30 m3/h时，偏度值变化范围在-0.18～0.234之间，峰度值变化范围在-0.438～0.527之间。为了更形象直观展现偏度和峰度与含沙浓度关系，把表中数据绘制成图13所示。

表5 流量10（±0.91）m3/h脉动压强的偏度系数与峰度系数

表6 流量30（±0.99）m3/h脉动压强的偏度系数与峰度系数

图13 偏度和峰度与含沙浓度相关关系

若偏度等于0，分布形态与正态分布相同，偏度大于0为右偏，即分布形态长尾在右；若偏度小于0为左偏，即分布形态长尾在左；偏度的绝对值越大，分布形态偏移程度越大。若峰度大于0，分布形态陡峭（瘦高），若峰度小于0，分布形态平缓（矮胖）。从图13可以看出，随着含沙浓度的增大，偏度值会有略微的增大，而峰度值围绕零上下波动，总体来说偏度和峰度与含沙浓度相关性较弱，故脉动压强概率密度分布接近正态分布。

3.5 脉动压强的频谱特性水流的脉动现象是有许多大小不一、不同幅值、不同频率、不同脉动强度的涡旋运动所引起的，壁面压强的脉动也是这些涡旋运动的反映[5]。对采集管道脉动压强的连续波动信号进行快速傅里叶变换（FFT），可以得到脉动压强的振幅谱、相位谱和功率谱，从而获得有压输沙管道脉动压强的频率分布。

非周期性连续时间信号（ft）的傅里叶变换可以表示为：

图14 清水工况下脉动压强功率谱

有压管道输沙过程中所产生的脉动压强是由具有一定能量的频率分量组成的，而功率谱密度则表征了这些频率分量所具有的能量平均值。以往的研究表明：清水湍流的紊动能量主要集中在0～20 Hz范围内，通常将0～2 Hz 称为低频范围，2～20 Hz 称为主频范围，而将大于20 Hz 称为高频范围[23-24]。本次试验在2～20 Hz范围出现次数最多，功率谱总能量占50%以上。图14为清水工况下管道上1#和4#位置的脉动压强功率谱分布，随着管中流量的增大，0～20 Hz范围内的脉动能量分量明显增多。

图15和图16 分别为流量10 m3/h和30 m3/h条件下不同含沙浓度引起的脉动压强功率谱分布情况，在相同流量条件下，随着含沙浓度的增加，脉动压强能量在0～20 Hz范围的分量逐渐增多，而大于50 Hz 的能量非常微弱。脉动压强波动与湍流能量衰减密切相关，泥沙颗粒与水流相互作用，改变了水流紊动结构。随着含沙浓度增高，浑水容重和黏度增加，紊流结构发生变化，小尺度旋涡明显减少，大中尺度旋涡增多，所产生的脉动压强周期长、振幅大、频率低[25]。

图15 流量10m3/h脉动压强能量谱（1#）

图16 流量30m3/h脉动压强功率谱（4#）

4 结论

通过设计水平有压输沙管道试验模型，根据高、超高、特高含沙量划分标准，以黄河细沙（d50=107 μm）为研究对象，配置不同含沙浓度（Cv=0～21.75%）的浑水，模拟流量分别为10（±0.91）、15（±0.28）、20（±0.28）、30（±0.99）m3/h条件下的管道输沙引起的脉动压强，得到以下结论：（1）相同流量下的时均压强沿程下降幅值随含沙浓度增大而增大，最大瞬时峰值压强也随含沙浓度增大而增大。泥沙存在对水流有一定的制紊作用，在相同流量情况下，随着含沙浓度的增加，相对脉动压强总趋势是降低的。（2）脉动压强概率密度接近正态分布，偏度和峰度系数与含沙浓度相关性较弱。清水条件下，随着流量的减小，其概率密度分布从矮胖型向瘦高型发展，脉动压强振幅降低，逐渐向均值靠拢，压强脉动强度随雷诺数增大而变大。均值压强和方差受含沙浓度影响较大，相同流量条件下，随着含沙浓度增加，均值出现不同程度偏移，而方差逐渐增大，概率密度分布从瘦高型发展成矮胖型。（3）脉动压强波动与湍流能量耗散有密切关系，泥沙与水流相互作用影响着管壁脉动压强的波动。含沙浓度增高，大中尺度旋涡增多，产生的脉动压强振幅大、频率低。在清水条件下随流量的增大，压强振幅逐渐增大，中低频能量有明显增加。相同流量条件下，随着含沙浓度增加，脉动能量在0～20 Hz范围的分量增多，大于50 Hz 的能量则非常微弱。