基于U肋横向影响线的轴重识别算法研究
马鹏飞, 安家禾, 张 斌, 朱 平, 赵 华
(湖南大学 风工程与桥梁工程湖南省重点实验室, 湖南 长沙 410082)
正交异性钢桥面作为钢箱梁普遍采用的一种桥面体系,已经被广泛地应用到了实际桥梁结构中[1]。但是,由于正交异性钢桥面本身是各组件(加劲肋、隔板和桥面板)焊接而成。焊接本身会对组件局部材料特性带来改变,正交异性钢桥面在连接焊缝处易产生疲劳开裂。此外,因为钢桥面直接承受车轮荷载,在重载车辆的反复作用下,其引起的应力变幅可能会很大。横隔板的存在导致内力影响线较短,在重型车辆荷载引起的应力变幅次数还会增多,这会增大疲劳开裂的可能性[2]。在正交异性钢桥面常见的破坏形式中,疲劳裂缝占比最大且疲劳开裂后的修检会给政府和管理部门带来一定的经济负担[3~4]。因此,有必要对正交异性钢桥面的车辆进行监控管制以延长其使用寿命。
为了对OSD桥面的车辆荷载进行识别,引入桥梁动态称重(Bridge Weigh-in-Motion: BWIM)的概念。 BWIM作为对桥梁结构车辆荷载有效识别工具,目前已经在钢梁桥、混凝土梁桥和斜拉桥等桥梁中得到了验证[5-10]。BWIM系统在OSD中的应用可以追溯到本世纪之初。早在1990年代末期就有诸多学者开展了关于BWIM系统在正交异性桥面中应用的可行性及其适用性的研究[9,12]。LCPC(法国国家路桥中心)于1996年第一次提出对正交异性钢桥面应用BWIM系统的概念[8];与此同时,OJIO[8]等也开展了BWIM在钢桥正交异性桥面中应用的可行性研究并且对实桥进行相应试验; DEMSPEY[9]等开启了BWIM在正交异性桥面板的应用中整体优化识别算法的研究以提高其在OSD中应用时的车轴识别精度(1999年);LAW[10]等通过有限元模拟钢梁桥并利用模态叠加的方法获得桥梁动力应变,最后依据运动方程求解得到车辆轴重信息;之后,有学者对OSD的受力性能开展研究,以探求BWIM 在OSD应用时的更多可能性。ZHU[11]通对正交异性桥面在动力荷载下的受力特性研究发现正交异性桥面的纵向U肋由于横隔板的加劲作用在动力荷载下其受力特点与多跨连续梁相似;XIAO[12]等根据正交异性桥面U肋的受力特点,首次提出利用去除整体效应成分的应变对车辆轴重进行识别 ;SUZUKI[13]通过对隔板、纵肋同时标定计算轴重,也得到了满意的识别结果。为了探索BWIM系统在OSD应用的更多可能性,对现有算法改进以提高算法的稳定性、降低识别误差是可行的途径,这为其能够应用到更多实际桥梁提供条件。
1 试验桥梁
根据研究内容,对实桥开展试验获得试验数据。该研究的试验基于广东省佛山佛陈新桥。佛陈新桥是一座三跨变截面连续梁桥,其主梁形式采用正交异性桥面板钢箱梁,该桥梁跨径布置在纵向上对称(58.51 m+112.8 m+58.51 m,总长229.82 m),主桥立面见图1。箱梁主截面为单箱单室,单幅桥宽15.75 m,在横向上单向三车道布置。具体的横向布置为:3.25 m(人行道+非机动车道)+3×3.75 m(机动车道)+1.25 m(路缘带),其箱梁具体形式见图2。佛陈新桥总共两幅,其主要的区别在于桥面铺装形式。其中一幅桥面铺装采用4.5 cm UHPC+3.5 cm沥青磨损层的薄层轻型组合桥面,另一幅桥采用4 cm+4 cm改性沥青SAM-13沥青铺装。本文所选取的试验桥梁为沥青铺装幅。

图1 主桥立面图(单位: cm)Figure 1 Elevation of fochen bridge (Unit:cm)
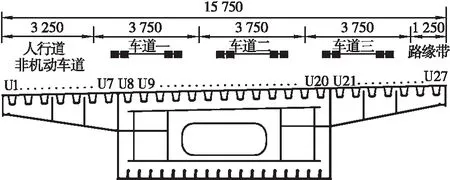
图2 一般横断面图(单位: mm)Figure 2 Cross section of the main girder (Unit:mm)
1.1 实桥试验-标定试验
该试验主要目的在于研究利用正交异性钢桥面板U肋的横向影响线识别桥面车辆的可行性。依据实际算法需求,对该桥面开展标定试验。
标定试验位置选取在桥梁中跨的等截面段,具体位置见图3的EF。选择该四分点的等截面段主要原因是有两点: ①减小桥梁整体效应对试验的影响;②有效避开连续梁桥支点变截面段。标定试验会在车道一和车道二进行,原因是车道三U肋在翼缘内,不能布置传感器。称重传感器的布置与试验车道在横向上相协调,因此,车道一纵肋U8~U13下缘处布置了应变传感器,车道二对应的在U14~U20布置传感器,具体布置情况见图4。车轴识别传感器的布置关于称重传感器对称,即在称重传感器前后2.5 m处各布置一排FAD传感器用于识别车辆车速、轴距等信息。

图3 标定截面具体位置图(单位: mm)Figure 3 Location of calibrated section (Unit:mm)

图4 传感器平面布置图(单位: mm)Figure 4 Layout of sensors on plane (Unit:mm)
在标定试验中,传感器所采集的皆为U肋的动态响应,动态应变的采集仪器是日本公司TML的DC-204,仪器的采样频率设置为512 Hz。动态应变的采集元件为扬州科动公司制造的KD4001。
此外,该试验所采用车辆为三轴车,见图5。试验分成2个工况进行,当标定车辆在车道一行驶时,记为工况1(共10趟有效数据);当标定车辆在车道二行驶时,记为工况2(共9趟有效数据)。
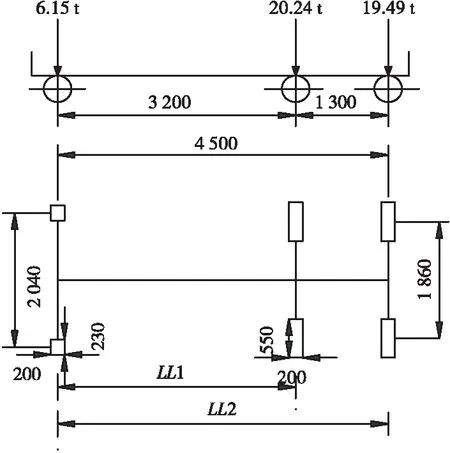
图5 标定车示意图(单位: mm)Figure 5 Figure of calibration trucks (Unit: mm)
1.2 实桥试验-静力试验
U肋横桥向上应力(纵向应力)的影响线是该方法求解辆轴重的必要条件。为了求得U肋的横向分布影响线,对该桥面板开展了静力试验。考虑到实桥横向加载难以控制其加载精度,拟采用本文的静力加载试验数据验证有限元模型,从而利用有限元模型的精准加载求得U肋横向分布影响线。
根据本文的需求,关注两个测点A5和B5处的静力加载试验数据,测点的具体位置如图6所示。A5为两相邻隔板中间(跨中截面)处U肋底部测点;对应地,B5为隔板截面(支点截面)处面板U肋底部测点。
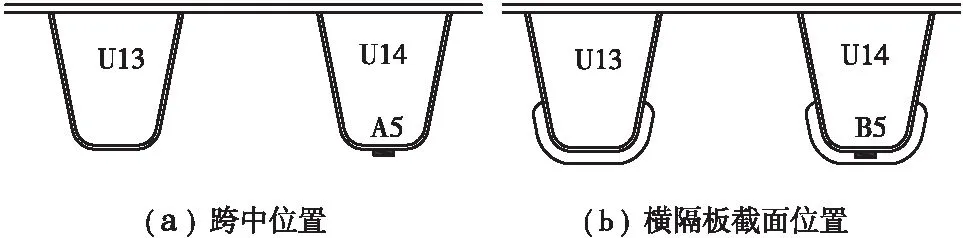
图6 测点布置图(单位: mm)Figure 6 Layout of the measuring points (Unit: mm)
试验的加载位置主要围绕U14(第二车道)展开,由于正交异性钢桥面的局部受力特性,测点的应力对加载位置比较敏感。因此,在开展该试验时拟采用6个工况进行加载,试验工况在横向上由3种不同的分布形式,即正U肋、骑U肋和U肋间;纵向上两种加载方式,即车辆两后轴(联轴)的中心线依次对齐横隔板和跨中,见图7。

(a) 横向加载方式
在静力试验中,采用日本TML的应变计作为采样元件,读取应变的仪器是江苏东华生产的DH3818静态应变测试仪。
2 基于U肋横向分布的轴重算法
正交异性钢桥面具备明显的局部的受力特性,当U肋在承担车辆轮载时在横向上产生明显的差异,即当车轮正压在U肋上方时,该U肋产生明显挠曲。当车轮偏离该加载位置时,相邻U肋的响应就会发生明显的变化。当车辆荷载在横向上移动时,U肋之间的应变变化存在一定的规律性。因此,可以通过研究车轮作用下相邻U肋之间的响应关系来确定该车辆的轴重情况。
当采用横向分布计算法对车辆的轴重进行计算时,首先要获得车辆在桥面上的位置。在已知横向位置条件下,换算得到车辆在理想加载位置时参考U肋的应变数据。在实际加载位置时,车辆在U肋上引起的应变响应是SN;假定将该车辆荷载在横向上移动横向距离D至理想记载位置(当车辆的轮载正压在U肋上方),此时车辆能够在U肋上产生的应变为PN。一般情况下,车辆的加载位置会偏离理想加载位置,所以需要借助钢桥面板的受力特性,换算求得该车辆在理想加载位置时的响应。计算过程参考下文,图8为某车辆轮载在理想加载位置下和非理想加载位置下U肋的应变关系。
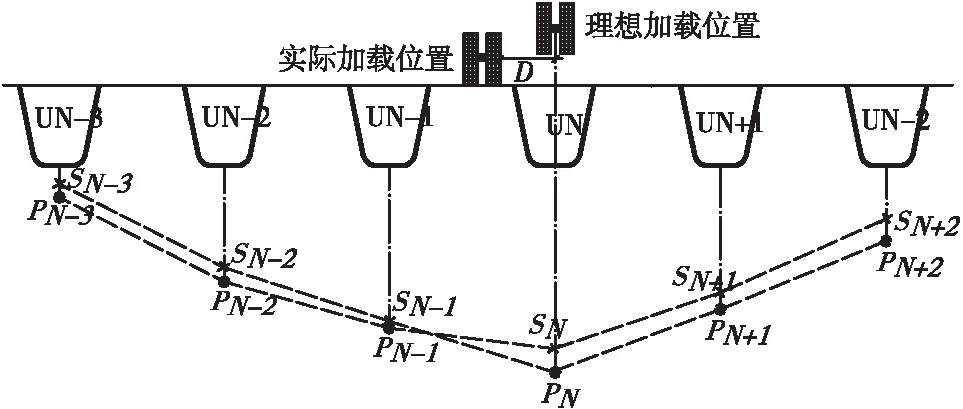
图8 U肋在不同加载条件下的应变Figure 8 Strain response of the U-ribs on different load cases

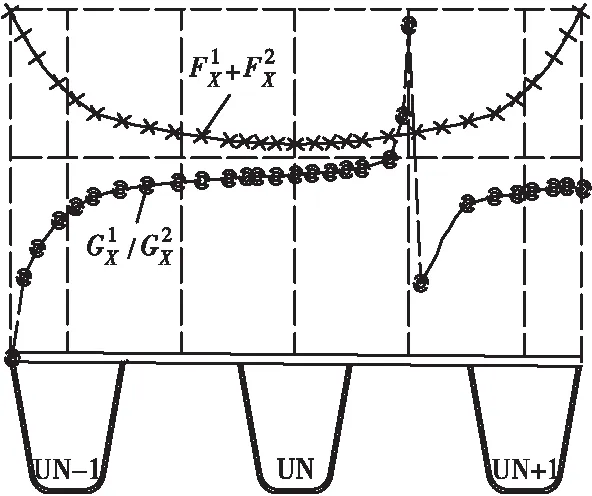
图和的横向变化Figure 9 Variation of laterally

(1)
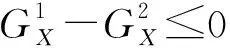
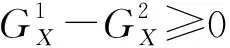

因此,车辆的横向位置可以由车辆在过桥时在不同U肋上所引起的应变大小数值关系求得。
当获得车辆横向位置时,就可以利用U肋的横向影响线求得U肋在理想加载位置下的应变响应。该应变与单位荷载下对应U肋上应变大小求比值就可以直接得到车辆的轴重信息。
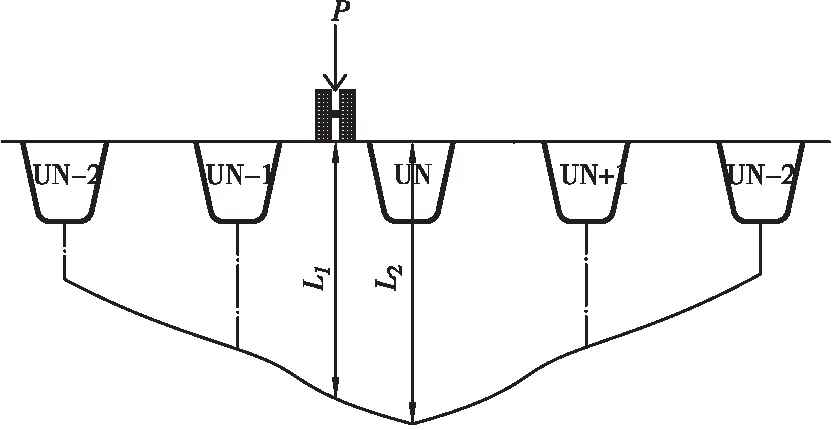
图10 车辆轴重求解示意图Figure 10 Calculation of axle loads
SN=PL1/W
(2)
式中:P为加载车辆的轮载;W为该截面上U肋下缘处的截面模量。
当荷载位于理想加载位置时,该轮载在横向分布影响线上对应的影响线数值是L2,此时U肋的应变大小可以表示为:

(3)
式中:L2为理想记载位置时U肋影响线数值。
所以,上述U肋由于加载位置的改变所引起的ΔN响应变化可以表示为:

(4)
所以,
(5)
由以上即可求得车轮荷载在理想加载条件下N#U肋上应变大小。通过对该应变与单位轮载加载所引起的应变求比值就可以得到该车辆的轮载大小。
Ws=PN/PS
(6)
3 轴重计算
根据第2节横向分布计算方法的算法理论可知,该算法在进行轴重计算的过程中大致分为两步:车辆在桥面上横向位置的确定和换算在理想加载位置下该车辆在参考U肋上所引起的应变响应。在求解车辆的横向位置时,需要事先获得参考U肋在横向上的应力影响线。因此本节将按照以下顺序展开:求解参考U肋在横桥向上应力(纵向应力)影响线、计算横向位置和求解轴重。
3.1 U肋横向影响线的计算
根据第2节横向分布算法的介绍,在对桥面车辆进行横向位置探测时需要事先求得U肋横向上的应力影响线。根据第1节的试验安排,拟采用本文的静力加载试验数据验证有限元模型。利用有限元模拟车辆横向加载的位置,即可实现理想车辆在理想位置的加载,从而求得U肋的横向分布影响线。
在采用有限元软件模拟车辆加载位置时,利用ANSYS建立该试验桥梁的钢主梁的节段模型,如图11所示。根据张龙威[16]等的研究成果,正交异性钢桥面板在静力加载情况下,其实际受力影响范围在纵向上不会大于两隔板之间的间距。因此,在对桥梁的静力试验进行模拟时,该有限元模型大小在纵向上拟采用4个隔板间距长度,两相邻隔板之间的间距为2.5m。出于对模型的边界约束的考虑,本文中对模型梁段两端各预留0.2m,模型中该箱梁节段的实际长度是10.4 m (0.2 m+2.5 m×4+0.2 m=10.4 m)。

图11 梁节段模型Figure 11 FE model of steel box girder
对该主梁节段进行有限元模拟时,主要采用实体、单元和壳单元,见图1和表1。模型中的钢梁部分均采用shell63壳单元模拟,桥面铺装的沥青材料则是利用solid45实体单元进行拟合。因为沥青铺装层分为两次摊铺,假定材料均为连续的各向同性的弹性材料,则沥青层之间利用节点耦合模拟。对于钢桥面板和桥面铺装层之间的连接,在此界面上,两层节点在连接处考虑其层间的滑移,故只对竖向的自由度进行耦合。此外,在对桥梁节段进行模拟时,不考虑焊缝。

表1 桥梁的结构几何和材料参数Table 1 Structural geometry and material parameters of bridges结构参数/mm材料参数面板厚横隔板厚腹板厚底板厚U肋厚钢板弹模/GPa沥青弹模/MPa钢材泊松比沥青泊松比1612242882101 0000.30.2
试验模型在具体的加载会在第2~第3道隔板的范围内进行,测点的位置距离实际模拟的边界较远。依据Saint Venan原理,有限元模型的边界条件对于测点处的结果影响较小,因此在实际模拟过程中对该节段模型的边界进行固结处理。
在建立有限元节段模型后,按照第1节静力试验方案对模型进行加载。表2为实际加载工况下的测点应变大小与有限元模拟的结果对比。由表2可知,有限元模拟的各个工况下参考点处的应变大小与实际加载工况下的数值大小接近,误差均在可接受范围内,说明该有限元模型能够有效地模拟该钢梁节段静力加载情况下U肋的实际应变大小。这也为通过有限元模型模拟静力加载试验求解U肋的横向分布影响线提供了可靠的依据。
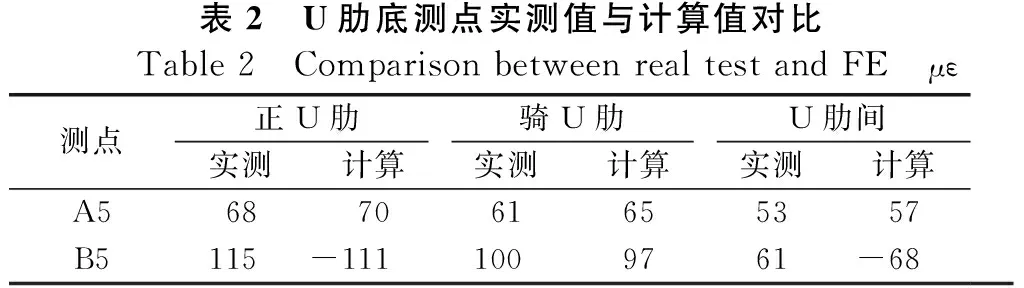
表2 U肋底测点实测值与计算值对比Table 2 Comparison between real test and FEμε测点正U肋骑U肋U肋间实测计算实测计算实测计算A5687061655357B5115-1111009761-68
根据上述有限元加载结果和实际加载结果的对比,证明有限元模型能够有效反映U肋测点的实际应变大小。在计算U肋的横向影响线时,同样采用有限元的加载方式,这样可以有效控制加载点的位置以便真实反映U肋纵向应力影响线在横向上的影响线。当选择截面上不同位置的标定U肋时,其横向的影响线之间也会有差异,因为标定截面上的腹板会对U8和U20进行局部加劲,导致其U肋上的应变会减小,不能够反映一般U肋作为承力构件时的实际横向影响线。给模型加载求解U肋在横向上的应力影响线时发现,能够对U肋造成明显影响的加载位置基本会在两个相邻U肋间距的范围内,所以在实桥试验中U9~U19的任何一条U肋的实际应变响应均能够作为横向分布算法求解轴重的依据。在计算U肋的横向影响线时,本文以U14作为参考。基于实际的模型的网格化划分,在求解U肋的横向影响线时,在标定截面的横向按顺序上选取了73个加载点设置荷载步,并计算每个荷载步下的参考U肋下缘处的应力。U14的横向上的应力影响线如图12所示,在静力加载条件下,U肋在横向上的影响会在两个U肋间距范围内。当在距离标定U14肋中心1000mm以后加载时,对U14的影响几乎可以忽略不计。此外,当加载的中心在U肋(-150,+150)范围内时,U14对加载位置不敏感,影响线的下降幅度较小;但是当加载在U14以外时,横向影响线的数值迅速下降,当加载位置到相邻U肋中心时对U14的影响只有0.3左右。

图12 U肋横向上的应力影响线(单位: mm)Figure 12 IL of U-ribs laterally(Unit: mm)
3.2 横向位置求解
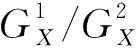
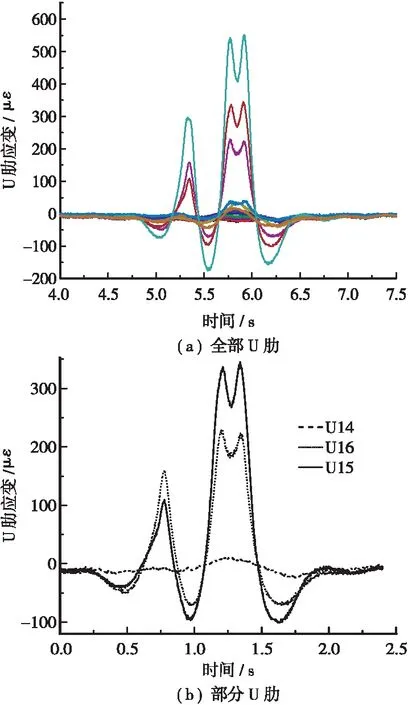
图13 工况二条件下第一趟跑车部分U肋试验数据Figure 13 response on the U-ribs based on load case 2
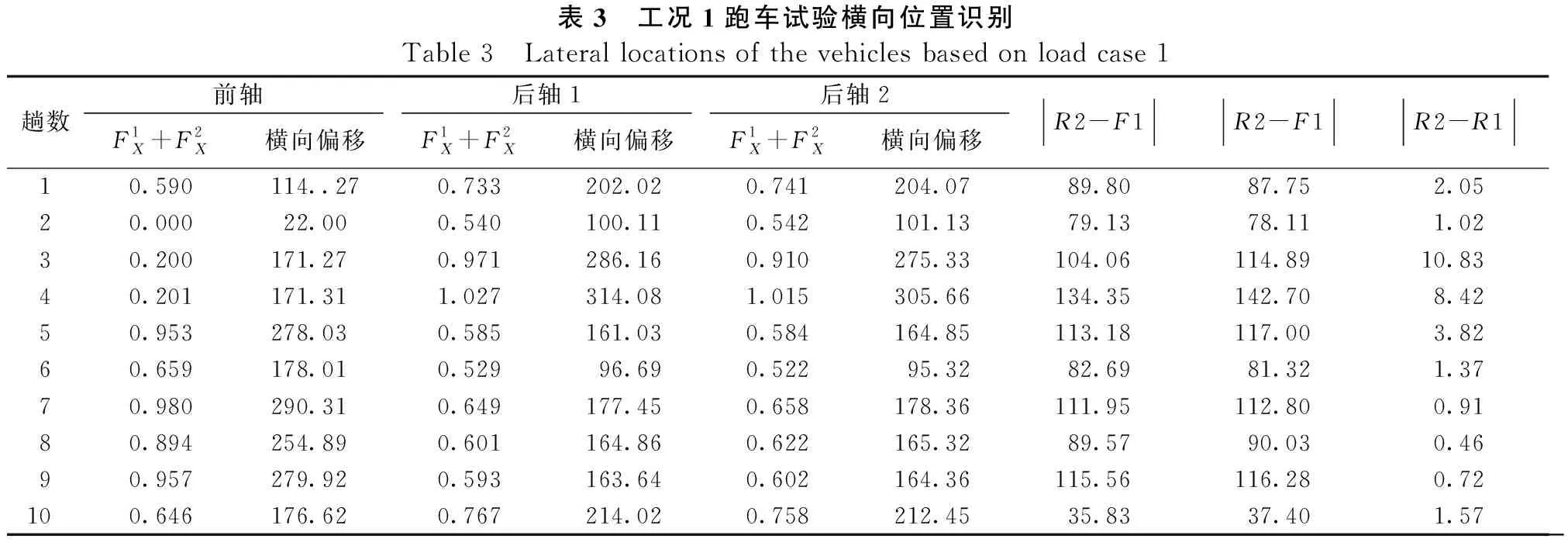
表3 工况1跑车试验横向位置识别Table 3 Lateral locations of the vehicles based on load case 1趟数前轴后轴1后轴2F1X+F2X横向偏移F1X+F2X横向偏移F1X+F2X横向偏移R2-F1R2-F1R2-R110.590114..270.733202.020.741204.0789.8087.752.0520.00022.000.540100.110.542101.1379.1378.111.0230.200171.270.971286.160.910275.33104.06114.8910.8340.201171.311.027314.081.015305.66134.35142.708.4250.953278.030.585161.030.584164.85113.18117.003.8260.659178.010.52996.690.52295.3282.6981.321.3770.980290.310.649177.450.658178.36111.95112.800.9180.894254.890.601164.860.622165.3289.5790.030.4690.957279.920.593163.640.602164.36115.56116.280.72100.646176.620.767214.020.758212.4535.8337.401.57

表4 工况2跑车试验横向位置识别结果Table 4 Lateral locations of the vehicles based on load case 2趟数前轴后轴1后轴2F1X+F2X横向偏移F1X+F2X横向偏移F1X+F2X横向偏移R2-F1R2-F1R2-R110.736203.190.51592.320.50990.30112.89110.872.0220.575158.310.24817.320.25518.87139.44140.991.5530.938258.510.611167.350.618169.1489.3791.161.7940.21012.110.423128.050.436131.43119.32115.943.3850.53298.060.862242.160.857541.89143.83144.100.2760.10057.080.780216.850.793220.96163.88159.774.1170.29650.180.614168.120.601164.86114.68117.943.2680.00025.000.390118.000.381114.7989.7993.003.2190.00022.000.400118.300.380114.7292.7296.303.58
3.3 车辆轴重求解
依据第2节的轴重计算算法介绍,横向分布轴重计算法在计算车辆轴重时通过对假定理想加载位置下的U肋应变和单位荷载条件的U肋应变求比值。假定理想加载位置下的U肋应变计算依据车辆跑车试验的U肋数据和车辆在桥面上的横向位置关系即可确定,单位荷载作用下的U肋应变计算求解借助于有限元ANSYS来求解。单位轮载在理想记载位置加载时的计算结果如图14所示,该图显示梁节段模型的应力结果。

图14 单位轮载在理想记载位置加载时的计算结果Figure 14 FE modeling result under unit single axle load
标定跑车试验时动力加载试验,标定车辆在经过桥梁标定断面时在U肋的应变对应的是动态应变。根据算法,实际的轴重计算是采用两个应变的比值:即车辆在假定理想加载位置处的应变比值和上述单位荷载在理想加载位置处对应U肋上产生的应变比值。对于前者的取值,由上节所述,采用每个车轴引起的波峰位置周围的35个应变值去平均值求得;后者的计算结果可以通过上述有限元模拟得到。由于有限元模拟的应变结果是静力加载试验下的应变值,而试验中的U肋应变时包含了车辆行驶对桥梁的冲击效应。本节对该主桥的车辆冲击系数不展开详细的讨论,而是直接采用张龙威的计算结果数值[17]。根据张的研究成果:桥梁在不同车速作用下的车辆对主桥结果的冲击效应存在差别。张研究了3个不同速度,即20、40和70 kM/h条件下车辆对主桥结构的冲击系数,计算结果分别是:1.062、1.103和1.137。根据试验中实际计算所得的车辆速度,本节在计算轴重时的车辆冲击系数采用1.069[18]。
横向分布计算方法的轴重识别结果汇总见表5。分析两个工况下的轴重识别结果: ① 两个后轴的轴重识别误差均在合理范围内,工况1的后轴识别误差在-3.94%~12.47%,工况2的识别误差在-2.79%~ 10.95%,只有个别趟跑车试验的识别结果误差较大,如工况1第1趟和工况2第6趟。② 前轴的轴重识别结果离散性较大,识别结果不稳定,主要原因可能是前轴横向位置识别结果不准确;横向位置的不准确会直接导致其在横向上的实际位置对参考U肋的影响计算不准确,可能原因分析见3.2。③ 总体上,后轴的轴重识别结果总优于前轴。④ 对比两个工况的识别结果,其识别结果误差很相近。

表5 轴重识别结果Table 5 Result of axle identification趟数工况1工况2A1/t误差/%A2/t误差/%A3/t误差/%A1/t误差/%A2/t误差/%A3/t误差/%15.61-8.7320.414.6822.7612.476.8010.5519.44-0.2819.67-2.7926.211.0319.44-0.2919.53-3.945.71-7.0919.46-0.1521.616.7536.485.4520.645.8721.837.906.180.4619.42-0.3321.576.5746.261.1819.47-0.1520.481.186.647.9620.887.1421.184.6456.9513.1521.639.5921.596.676.658.0619.932.2721.455.9766.404.1220.625.7621.435.916.01-2.2520.746.4322.4610.9576.221.2418.29-6.3819.77-2.346.251.6420.505.1820.501.2886.11-0.5119.43-0.3519.72-2.557.1115.6420.525.2920.511.3297.3118.0420.485.0121.154.516.043.6619.09-2.0521.275.06106.8710.8020.062.8919.881.75//////均值/4.58/2.66/3.16/3.68/2.61/4.41STV/7.69/4.53/2.27/7.28/3.45/3.98
4 结论
a. 结合车辆在正交异性钢桥面上时其纵向U肋的响应,提出了关于利用U肋横桥上的影响线计算车辆轴重的算法,并在理论上证明其可行性。
b. 提出利用有限元模型标定U肋横向影响线的方法,计算结果表明有限元模拟的影响线能够真实反映U肋的受力,且该方法能够精确控制加载位置。
c. 基于U肋横桥上的影响线轴重识别计算算法能够有效地对车辆过桥时的横向位置进行识别,利用该方法对车辆轴重进行识别的结果表明:该方法有效地识别桥面车辆荷载,总体上识别结果较为理想,为OSD的轴重识别提供了一种可能性。但是,前轴的结果总是劣于后轴的识别结果。

