基于无应力正装迭代法的大跨混凝土斜拉桥合理施工状态分析
吴月星,张博恒,周建庭,严仁章
(1.重庆交通大学 土木工程学院,重庆 400074;2. 重庆市设计院,重庆 400015)
从1955年瑞典修建主跨为182.6 m的现代第一座斜拉桥—Stromsund桥[1]至2019年1月9日正式开工建设的目前世界最大跨斜拉桥—主跨1 176 m常泰过江通道主航道桥,斜拉桥取得飞越式发展。混凝土斜拉桥同样如此,1962年世界第一座现代混凝土斜拉桥—马拉开波湖桥[2]的出现揭开了混凝土斜拉桥的序幕,而目前世界上最大跨径的混凝土斜拉桥Skarnsunder桥[1]主跨已达530 m,坐落于挪威。混凝土斜拉桥具有诸多优点:拉索受拉,混凝土承压,发挥各自优势;恒载效应较活载效应所占比例大,由活载引起的下挠值较小,全过程应力变化幅较小。然而,当混凝土斜拉桥跨径超过300 m时,作为复杂高次超静定结构体系的混凝土斜拉桥设计与施工变得复杂。
大跨混凝土斜拉桥包含合理成桥状态与合理施工状态[3]。在大跨混凝土斜拉桥计算分析中,首先应确定合理成桥状态,再确定施工各个阶段的中间状态—合理施工状态。合理成桥状态容易获取,最小弯曲能法结合影响矩阵法最为快速高效。合理施工状态的确定难度较大,常见的计算方法有前进分析法、倒退分析法[4]、正装迭代法、倒拆 — 正装交互迭代法、无应力状态法[5]等。现有单一的计算方法都有一定局限性,如前进分析法无法确定斜拉索的初始张拉力及立模标高;倒退分析法与正常施工工序相反,且无法考虑混凝土时变效应及几何非线性的影响;倒拆—正装交互迭代法迭代过程过于繁琐,每次迭代需建立一套倒拆分析模型,且需要考虑混凝土时变效应的影响,反复迭代,计算量较大;正装迭代法收敛速度过慢,求解时间较长;无应力状态法更适用于无需考虑混凝土时变效应的钢结构桥梁。
综上所述,单一的计算方法均无法完美确定斜拉桥合理施工状态。针对大跨混凝土斜拉桥合理施工状态确定难度大的问题,依托某主跨300 m的大跨混凝土斜拉桥,利用Midas软件建立空间有限元模型,提出将无应力状态法与正装迭代法相结合,以确定大跨混凝土斜拉桥合理施工状态。
1 工程概况
本桥为主跨300 m的预应力混凝土分离式双箱斜拉桥,桥跨组合为150 m+300 m+150 m,主桥长600 m,采用双塔、双索面、密索、对称扇形布置、塔梁分离的漂浮体系结构。为了提高主梁刚度、改善结构动力特性,两岸各设一辅助墩,辅助墩距交界墩75 m。主梁采用预应力砼分离式倒梯形断面,梁中心高3 m,箱梁全宽31.5 m。主桥标准段的桥面路幅分布形式为:2.5 m人行道+1.5 m锚索区+11.5 m车行道+0.5 m分隔带+11.5 m车行道+1.5 m锚索区+2.5 m人行道。索塔采用“H”形索塔、空心薄壁箱型截面。上塔柱高44.571 m,中塔柱高43.379 m,下塔柱高22.4 m。斜拉索采用高强低松弛镀锌钢绞线。大桥总体布置及主梁典型断面如图1、图2所示。
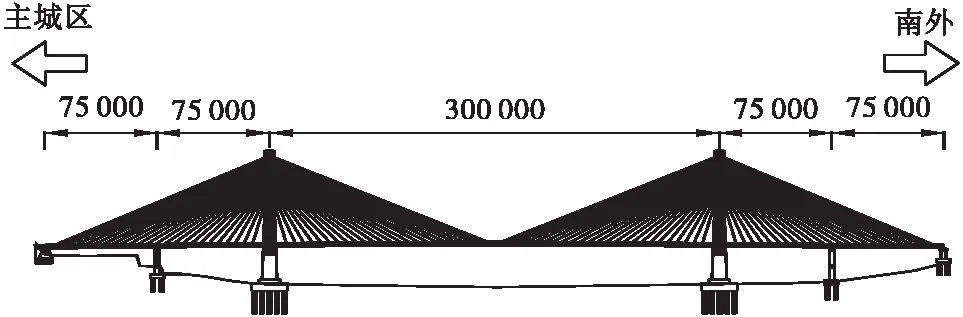
图1 大桥总体布置图(单位:mm)Figure 1 General layout of bridge (Unit: mm)

图2 主梁典型断面图(单位:mm)Figure 2 Typical section of main girder (Unit: mm)
2 无应力正装迭代法相关理论总结及实现流程
2.1 无应力状态法基本理论
对于结构本身,外荷载、边界情况给定,不论施工过程如何,只要保证构件激活时是以无应力状态量进行,最终结果与一次落架结果相同。对于斜拉桥结构,在施工过程合理的前提下,不管中间过程如何施工,拉索如何张拉调整,只要其最终状态的无应力状态量与一次落架无应力状态量相同,则两者最终内力与位移一致[6-9]。
2.2 无应力状态量计算
2.2.1拉索无应力索长计算
拉索以无应力索长控制。拉索无应力索长是指斜拉桥拉索单元两端的几何长度同拉索单元由轴力引起伸长量之间的差值。当制造拉索所配置无应力长度比设计长度长,施工过程中会出现拉索施工张拉力不能达到设计值;而拉索制造无应力长度比设计长度短时,拉索的有效锚固长度将无法得到满足。常用的拉索无应力索长计算方法是基于悬链线理论的精准算法。索力对应的水平分力是求解拉索无应力长度的关键因素,需要迭代才能得到精确结果。
2.2.2主梁、主塔无应力曲率计算
主梁、主塔以无应力长度与无应力曲率控制。Midas软件中可通过勾选“切线拼装”保证主梁、主塔构件以无应力状态拼装。特别是为了满足主梁线形的连续性,合龙段合龙时也应以无应力状态激活,通常可采用调索或施加临时荷载的方式,使合龙段两侧最大悬臂端不出现转角位移与水平位移,满足无应力安装条件。
2.3 考虑收缩徐变效应的无应力正装迭代法实现流程
2.3.1索力迭代
根据斜拉桥实际施工过程,建立分阶段施工有限元模型,考虑混凝土收缩徐变效应,采用无应力状态正装分析,拉索以合理成桥状态时拉索对应的无应力长度进行激活,主梁、主塔以无应力状态进行拼装。经过一次无应力正装分析,斜拉桥最终成桥状态与一次落架内力、线形不闭合。由无应力状态法基本原理可知,收缩徐变效应改变了结构构件无应力状态量。若要实现闭合,必须调整施工过程中的无应力状态量,可通过迭代分析解决不闭合问题,具体流程如图3所示。
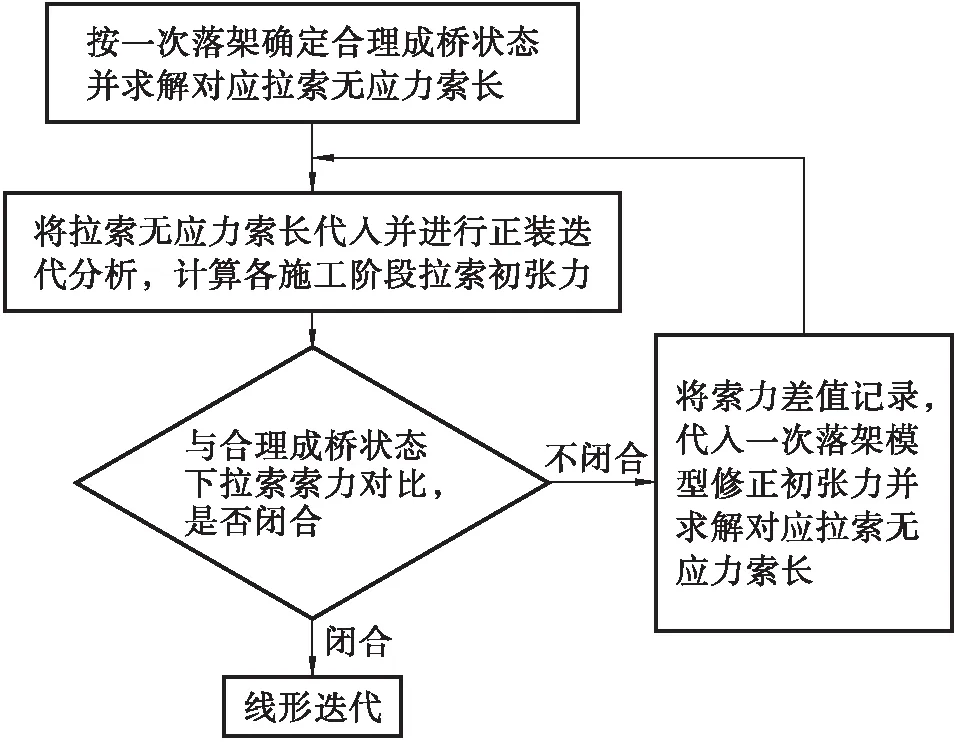
图3 索力迭代流程图Figure 3 Iterative flow chart of cable force
按照上述步骤,采用差值迭代调整无应力索长的方法,将第一次前进分析得到的成桥索力值与合理成桥状态的索力值做差,将该差值修正到成桥索力中,重新计算斜拉索无应力索长,以新的无应力索长进行下一轮计算。
2.3.2线形迭代
为了保证成桥后桥面线形合理、平顺,需在各主梁节段施工时,通过立模抛高的方式赋予梁体抛高值,以此来抵消施工变形,使施工完毕后达到设计线形,该过程需进行线形迭代计算。线形迭代实质是对建模坐标考虑预拱度的修正,使斜拉桥成桥后的主梁标高达到设计标高。具体流程如图4所示。

图4 线形迭代流程图Figure 4 Iterative flow chart of alignment
在进行线形迭代的时候,对建模坐标进行修正迭代,以此保证收缩徐变完成后且在考虑二分之一活载工况下,主梁线形达到设计线形。计算公式为:
H第一次修正=H施工预拱度+H成桥预拱度
(1)
H第二次修正=H第一次迭代线形-H设计
(2)
3 工程应用
依托某主跨300 m大跨混凝土斜拉桥,以最小弯曲能量法结合影响矩阵法确定的合理成桥状态为基础,基于无应力正装迭代法相关原理,以该状态下拉索对应的无应力长度做施工阶段正装分析消除收缩徐变效应产生的影响,并获取分阶段施工的关键控制参数。无应力正装迭代法完整迭代流程如图5所示。

图5 无应力正装迭代法完整迭代流程Figure 5 Complete iteration process of stress-free forward iteration method
3.1 有限元模型
主桥采用前支点挂篮工法悬臂浇筑施工,由索塔朝两侧对称施工。主桥施工顺序为:完成下部结构施工后,然后进行索塔上部施工;主梁0#~2#节段采用搭支架平台,现浇方式施工;主梁从3#(3'#)节段开始采用前支点挂篮悬臂施工,直至悬臂施工结束;先边跨合龙,再中跨合龙;合龙后进行全桥二次索力调整;进行桥面二期铺装、安装桥面附属设施。为分析各不闭合因素对斜拉桥最终成桥受力影响程度,建立Midas倒拆、正装有限元模型,主梁、索塔采用梁单元模拟,斜拉索采用桁架单元模拟。悬臂按照施工节段分成24个节段,每个边跨现浇段长3.5 m,划分为2个单元,每个边跨合龙段为1个单元,中跨合龙段为2个单元,主梁一共划分为206个单元,每个桥塔按照施工节段及其截面变化情况分为108个单元。每个前支点挂篮采用前后两个集中力进行模拟,边、中跨配重也采用集中力进行模拟。主塔与大地采用一般支撑,约束全部自由度;辅助墩处支座模拟为一般支撑,释放Dx、Ry、Rz方向自由度;永久支座模拟为一般支撑,释放Dx、Rx、Ry、Rz方向自由度;斜拉索与主梁、主塔的连接用主从约束(约束所有自由度)进行模拟;主梁受到主塔的侧向约束用弹性连接中的受压,模型如图6所示。

图6 全桥有限元模型Figure 6 Finite element model of cable-stayed bridge
3.2 计算结果及分析
由图7~图10可知:无应力状态法计算斜拉索合理施工状态时,在考虑混凝土收缩徐变效应的情况下,会出现最终成桥状态与目标状态(合理成桥状态)不闭合现象。基于无应力状态基本原理可知,不闭合的实质是施工时混凝土收缩徐变效应改变了构件的无应力状态量,收缩徐变发生以后,结构无应力状态量己经与设计时结构无应力状态量不同,即考虑与不考虑收缩徐变后的结构将为两个不同的结构。
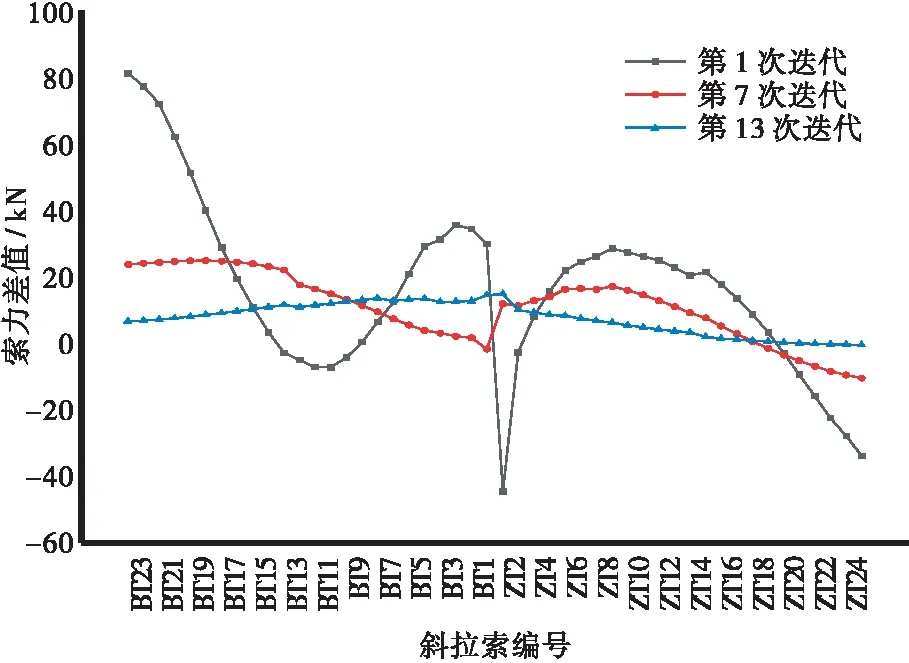
图7 不同次数迭代后成桥索力与目标索力差值对比Figure 7 Comparison of the difference between completed bridge cable force and target ones after different iterations

图8 不同次数迭代后成桥弯矩与目标弯矩对比Figure 8 Comparison of completed bridge moment and target moment after different iterations

图9 13次迭代后成桥主梁应力与目标应力差值对比Figure 9 Comparison of stress difference between main girder and target stress after thirteen iterations
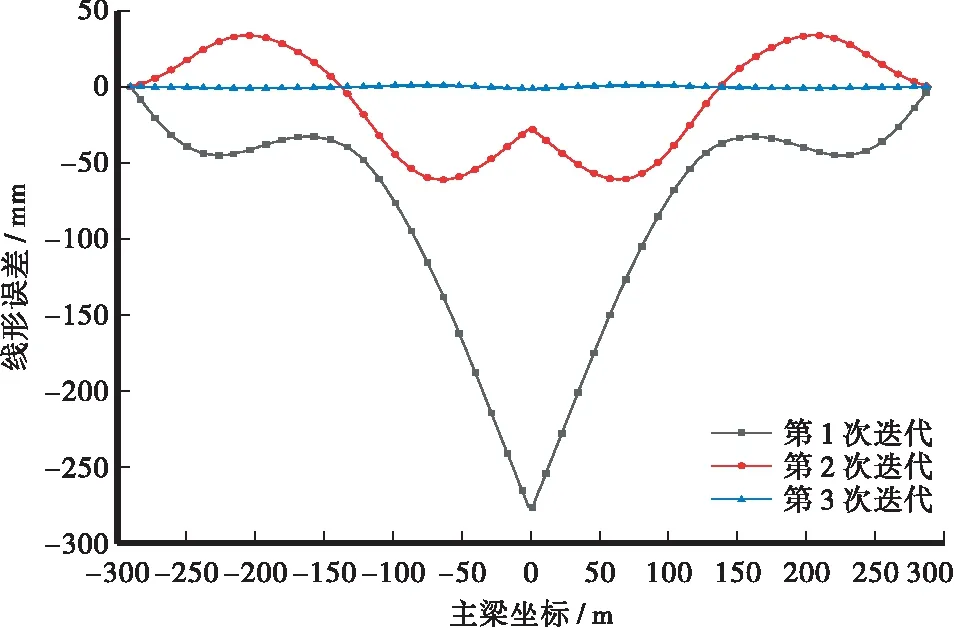
图10 不同次数迭代后线形差值对比Figure 10 Comparison of alignmentdifferences after different iterations
采用无应力正装迭代法,经过13次迭代分析后,成桥索力与目标闭合,最终索力差值可控制在0.5%以内。13次迭代过程中,主梁弯矩逐渐向目标弯矩靠近,迭代分析结束后,两者差值无法达到完全闭合。虽然主梁成桥弯矩与目标弯矩仍存在一定差值,但主梁作为轴向压弯构件,拉索提供的强大轴向力下,主梁主要以轴向受压为主。13次迭代后,主梁上缘应力值与目标上缘应力值相比,最大增量为0.38 MPa;主梁下缘应力值与目标下缘应力值相比,最大增量为-0.21 MPa,差值较小,对斜拉桥主梁受力影响较小,在工程可接受范围内。主梁线形经过3次迭代后,线形差值可完全消除。线形迭代速度较索力、弯矩迭代速度更快。
综上所述,可采用无应力正装迭代分析消除大跨混凝土斜拉桥索力、线形不闭合问题,但索力、弯矩、线形无法同时实现闭合,须作出取舍。成桥弯矩虽与目标弯矩有偏差,但应力变化值较小,在工程许可范围以内。
3.3 合理施工状态关键控制参数获取
3.3.1施工阶段拉索索力及无应力长度
在分阶段张拉施工过程中,为保证张拉过程中索的安全,对拉索进行分批次张拉,终张拉采用无应力长度进行调索,以合理成桥状态的无应力长度为目标状态,将拉索调至目标无应力长度。施工阶段拉索索力与无应力长度是在索力与线性计算闭合后的基础上提取。
由无应力状态法基本理论可知,无应力索长的改变值对应唯一索力改变量,施工过程索力控制可按锚头拔出量作为索力控制的依据。无应力状态法是按各构件的无应力状态量,以求解中间状态拉索的初张力。在实际施工控制中以索力值为主,锚头拔出量为辅。
本桥采用前支点挂篮悬臂浇筑施工方法,为保证浇筑过程中挂篮受力安全将对拉索采用分阶段张拉形式。张拉分3次,第1次张拉为混凝土浇筑前,索力一般为对应施工阶段拉索索力的30%~40%;第2次张拉为混凝土浇筑一半后,索力一般为对应施工阶段拉索索力的60%~70%;第3次张拉为混凝土浇筑完成后,达到对应施工阶段拉索索力100%。
斜拉索第1次张拉与第2次张拉以索力值控制即可,无须精确计算拉索的锚头拔出量。经两次索力张拉后,按施工阶段索力值张拉,并记录锚头拔出量的原始数据作为张拉是否到位的判断依据,以索力与锚头拔出量双控。
3.3.2预拱度设置
由于斜拉桥结构在活载和恒载的长期作用以及材料本身的收缩徐变影响将产生较大挠度,从而逐渐影响主梁运营,而主梁线形是影响斜拉桥运营过程中行车安全、稳定以及舒适的重要因素。
为了保证成桥后桥面线形平顺,运营状态良好,需给予主梁各个节段相应的抛高值,该抛高值可在立模标高时赋予预拱度加以考虑。因此,在施工过程中,立模标高需设置一定的预拱度,以此抵消施工中产生的各种因素引起的变形,使建成后的桥梁线形达到理论标高。
设计标高是指桥梁结构在正常运营下,收缩徐变基本完成(竣工5 a后)并考虑二分之一静活载时对应的标高。立模标高是为控制了施工状态主梁线形所设置的标高,本桥主梁采用悬臂浇筑施工的立模标高计算公式为:
(3)

因此,基于无应力正装迭代法确定的合理施工状态,获取施工过程拉索索力、无应力索长、锚头拔出量以及立模标高等施工控制关键参数,指导现场施工。
4 结论
针对大跨混凝土斜拉桥合理施工状态确定难的问题,依托某主跨300 m的大跨混凝土斜拉桥,利用Midas软件建立空间有限元模型,基于无应力状态法与正装迭代相结合的计算方法,确定其合理施工状态,得出考虑收缩徐变效应后无应力正装迭代收敛本质及相关迭代规律。基于确定的合理成桥状态,获取施工控制关键参数,即拉索初张力、无应力索长、锚头拔出量、主梁立模标高等,以指导本桥施工。主要结论如下:
a.再次验证了无应力状态法理论。即不考虑收缩徐变效应时,只要保证斜拉桥结构无应力状态量一致,一次落架成桥的目标状态与分阶段施工成桥最终状态的内力、位移、索力能够较好的吻合;不考虑收缩徐变时,无应力状态法可完全解决不闭合问题。在考虑混凝土收缩和徐变效应后,构件无应力状态量会随施工过程发生变化,导致最终成桥状态与目标值状态不闭合。实质上,考虑与不考虑收缩徐变的成桥状态下结构的最终状态的无应力状态量是不一样,即两者结构是不同的结构,要实现闭合,需调整无应力状态量进行迭代分析。
b. 采用无应力正装迭代法,经过13次迭代分析后,成桥索力与目标闭合,最终索力差值可控制在0.5%以内。13次迭代过程中,主梁弯矩逐渐向目标弯矩靠近,迭代分析结束后,两者差值无法达到完全闭合。虽然主梁成桥弯矩与目标弯矩仍存在一定差值,但主梁作为轴向压弯构件,拉索提供的强大轴向力下,主梁主要以轴向受压为主。13次迭代后,主梁上缘应力值与目标上缘应力值相比,最大增量为0.38 MPa;主梁下缘应力值与目标下缘应力值相比,最大增量为-0.21 MPa,差值较小,对斜拉桥主梁受力影响较小,在工程可接受范围内。主梁线形经过3次迭代后,线形差值可完全消除。线形迭代速度较索力、弯矩迭代速度更快。可采用无应力正装迭代分析消除大跨混凝土斜拉桥索力、线形不闭合问题,但索力、弯矩、线形无法同时实现闭合,须作出取舍。成桥弯矩虽与目标弯矩有偏差,但应力变化值较小,在工程许可范围以内。
c.经过无应力状态正装迭代法进行迭代计算,使斜拉桥索力达到了闭合,通过对主梁线形预拱度进行修正,抵消混凝土单元的无应力长度和曲率变化的影响,使线形达到设计线形,内力与设计值靠近以达到设计要求。在索力、线形闭合基础上,提取拉索索力、无应力索长、锚头拔出量以及立模标高等施工过程参数,以此指导现场施工。
本研究可为类似大跨混凝土斜拉桥施工(控制)提供有益借鉴。

