桥梁结构地震响应的接触效应及影响因素分析
王桂萱, 葛政青, 尹训强, 秦建敏
(大连大学 土木工程技术研究与开发中心,辽宁 大连 116622)
桥梁工程中经常会遇到结构之间动力相互作用的情况,比如桥墩或桩与地基、土体与结构交界面,以及桥梁上部结构关键构件间,都存在复杂的接触非线性问题。目前科研工作者们对于接触效应问题的分析,主要集中于桥墩或桩与地基土之间[1-5],而对于桥梁上部结构关键部位的接触非线性研究成果较少。已有的研究大多数没有考虑到接触面之间可能发生的滑移或者分离状态[6-8],此种情况会使得桥梁的地震响应计算分析产生偏差。因此,在数值模拟中,研究接触连接特性对桥梁上部结构间的规律与影响程度具有重要的理论与现实价值。本文采用通用有限元软件ANSYS,首先对Goodman单元的刚度系数进行率定及验证,然后对上部结构地震响应的接触效应以及影响因素分别进行分析。
1 桥梁结构地震响应有限元模型
1.1 上部结构间界面接触问题的实现
接触问题属于典型的非线性问题,对于非线性问题的计算常有不收敛的情况发生。ANSYS中具有较多的接触问题的数值计算方法,比如拉格朗日乘子法、罚方法、MPC算法以及增广的拉格朗日乘子法等,其中,增广的拉格朗日乘子法是拉格朗日乘子法与罚方法的有机结合,能够用于解决约束条件下的优化问题,增加了接触计算时的鲁棒性,使其更容易收敛。因此本文选取增广的拉格朗日乘子法用于接触问题的计算。
1.2 Goodman单元的使用
考虑接触效应问题自然要建立相应地接触单元来进行分析,有限元软件ANSYS中接触单元选用Goodman单元(无厚度单元)来模拟接触面的非线性行为。Goodman单元是Goodman[10]在1968年基于弹簧刚度的概念提出的应用于岩土力学的节理单元,该单元假定没有厚度只有长度,具有4个节点,两接触面是充分接触的,如图1所示。它是由两片长度都为L的接触面12和接触面34组成,且两接触面12和34之间有无数微小的弹簧所连接[11]。
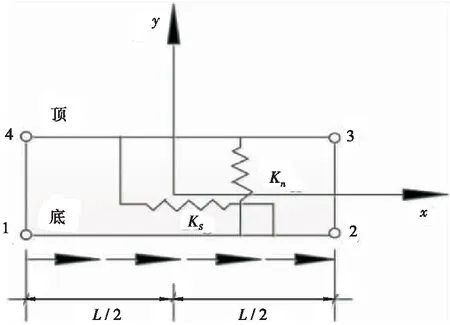
图1 Goodman单元Figure 1 Goodman element
1.3 单元参数的率定及验证
1.3.1Goodman单元刚度系数的率定
使用Goodman单元进行接触面模拟时,需要定义3个重要的参数[12]:法向刚度系数Kn、切向刚度系数Ks和接触摩擦系数Mu。其中需要对Kn和Ks进行率定。率定的主要思路是有限元模型在有接触单元时关键节点的位移与无接触单元时的位移进行比较,当位移误差较小时可以认为此时的刚度系数取值使得有限元模型在有接触单元时也没有发生滑移、分离等行为,为率定的合理取值。在此,提出一个率定式:Kn=αEc,其中α为比例因子,取1、10、20、50、100、200进行率定;Ec为混凝土弹性模量(数值模拟与振动台试验均用C40混凝土),取值根据《混凝土结构设计规范》(GB50010-2010)[13]见表1。

表1 混凝土的弹性模量 Table 1 Elastic modulus of concrete ×104 MPa混凝土强度等级C15C20C25C30C35C40C45C50Ec2.202.552.803.003.153.253.353.45
率定过程中选取有限元模型关键节点的位移进行计算,分别选取峰值加速度为0.1g、0.2g、0.3g的El centro波作为输入地震动,位移峰值变化情况整理如表2~表4所示。
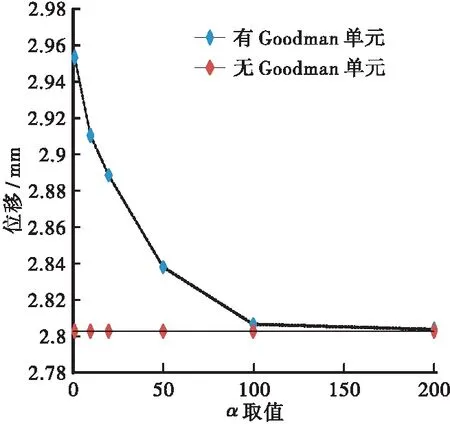
根据表2、表3和表4将不同地震动峰值加速度下有限元模型有无Goodman单元时的位移峰值绘制成折线图,如图2所示。
分析表2~表4和图2中3张变化图所得:α在0.1g、0.2g、0.3g下取值小于100时,位移峰值变化都很明显,此时Goodman单元的法向刚度不是一个定量,根据Goodman单元的物理定义可知此时因为刚度取值较小使得设置Goodman单元的两接触面之间发生了相互嵌入的现象;α取值大于100时,有无Goodman单元位移变化差距都很小,此时可认为两接触面之间不会发生嵌入现象,所以α取100时,即C40混凝土弹性模量的100倍是Goodman单元法向刚度Kn的较合理取值。对于Goodman单元切向刚度Ks的率定,我们根据混凝土材料特性关系式(1)求得。
2004年部署在洼陷构造低部位的车66井完钻,在沙三下首获高产工业油气流,继而在其南部部署车660井,又喜获成功。随后向北、西、南三面快

表2 0.1g下位移峰值变化Table 2 Peak displacement variation under 0.1g地震动峰值加速度比例因子α位移峰值/mm12.953 67102.910 37202.889 210.1g502.838 461002.807 152002.803 98无Goodman单元2.802 849
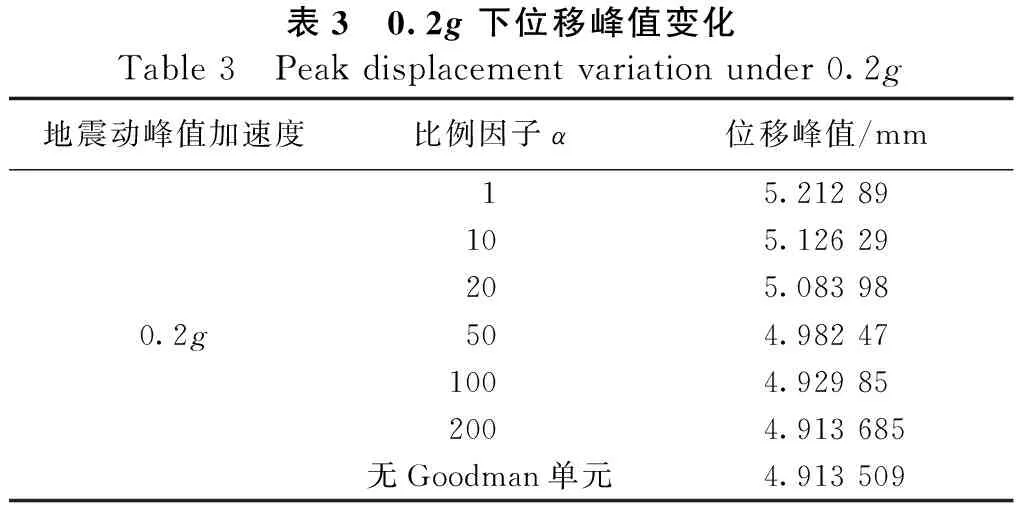
表3 0.2g下位移峰值变化Table 3 Peak displacement variation under 0.2g地震动峰值加速度比例因子α位移峰值/mm15.212 89105.126 29205.083 980.2g504.982 471004.929 852004.913 685无Goodman单元4.913 509
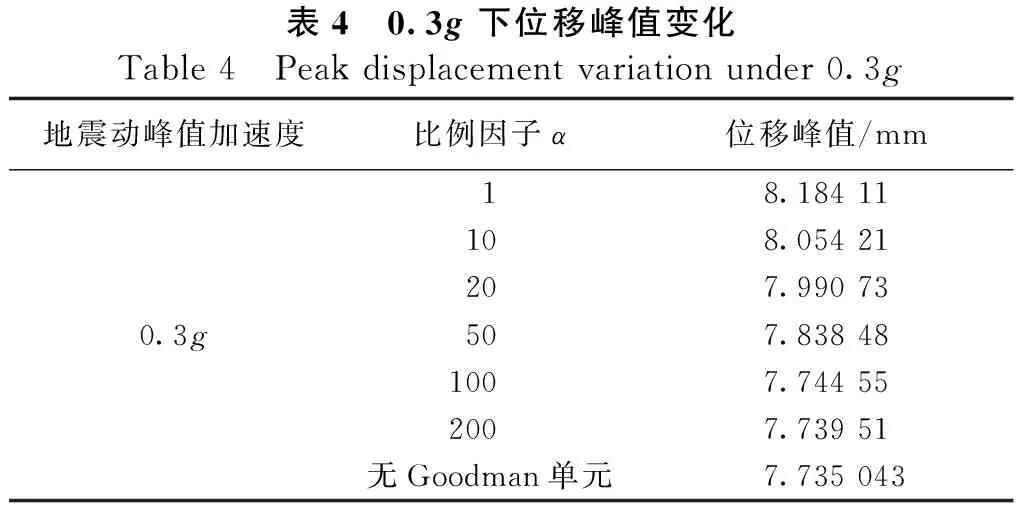
表4 0.3g下位移峰值变化Table 4 Peak displacement variation under 0.3g地震动峰值加速度比例因子α位移峰值/mm18.184 11108.054 21207.990 730.3g507.838 481007.744 552007.739 51无Goodman单元7.735 043
(a)0.1g (b)0.2g (c)0.3g
(1)
式中:G为混凝土的剪切模量;E为混凝土的弹性模量;ν为混凝土的泊松比,C40混凝土取0.24。
由式(1)计算可得:E=2.48G,此时Goodman单元的法向刚度与切向刚度的关系式大致为Kn=2.48Ks,即Ks取1.31×106N/mm2(较合理值)。
1.3.2验证Goodman单元刚度系数率定的准确性
验证的主要思路是:地震动依旧选取Elcentro波通过增大地震动峰值加速度的方式进行有限元数值计算(有接触单元)获取关键节点的加速度、位移及应变峰值与振动台试验实测(无接触单元)所得的加速度、位移及应变峰值进行误差比较分析。
a. 振动台试验介绍。
以某实际高架桥梁结构选取其中两跨作为研究对象,跨径组合为2×21 m,上部结构为钢筋混凝土箱梁,采用HPB400钢筋,C40混凝土,其截面形式为单箱单室截面,如图3所示。下部结构为混凝土矩形单墩,1#~3#桥墩高度均为9 m,截面尺寸均为3 m×1.5 m。桥梁与墩之间设置橡胶活动支座,桥墩底部将底座与振动台台面锚固连接。本试验采用1∶10的缩尺比例进行建模,图4给出了其实物图。

图3 混凝土主梁横截面图(单位:cm)Figure 3 Cross-section of concrete girder(Unit:cm)

图4 缩尺模型Figure 4 The scale model of continuous girder bridge
试验是在中国地震局工程力学研究所(北京东燕郊园区)恢先地震工程综合实验室进行的,原型桥与模型桥的相似关系如表5所示。由于比例缩尺的影响,需要在模型桥梁上部设置一定的配重,共放置52块20 kg的配重块。试验的加载工况如表6所示。
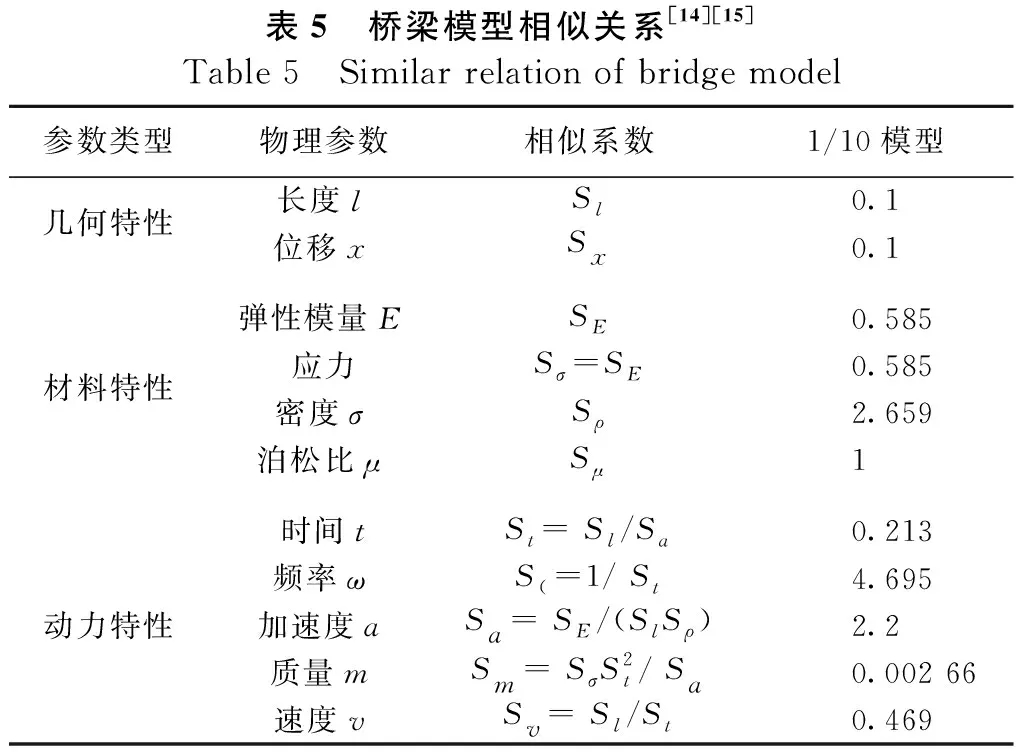
表5 桥梁模型相似关系[14][15]Table 5 Similar relation of bridge model参数类型物理参数相似系数1/10模型几何特性长度lSl0.1位移xSx0.1弹性模量ESE0.585材料特性应力Sσ=SE0.585密度σSρ2.659泊松比μSμ1时间tSt= Sl/Sa0.213频率ωS(=1/ St4.695动力特性加速度aSa = SE /(SlSρ)2.2质量mSm= SσS2t/ Sa0.002 66速度vSv= Sl/St0.469

表6 加载工况[16]Table 6 Condition of loading试验内容工况输入波形峰值加速度(×g)扫频试验1白噪声0.07一级加载2El centro波0.2扫频试验3白噪声0.07二级加载4El centro波0.3扫频试验5白噪声0.07三级加载6El centro波0.4扫频试验7白噪声0.07四级加载8El centro波0.5扫频试验9白噪声0.07五级加载10El centro波0.6
b. 模型试验结果对比分析。
地震动峰值加速度选取了0.4g、0.5g、0.6g这3组进行验证。有限元数值计算结果及振动台试验结果(测点选择中间跨接触位置)分别如表7和表8所示。
对比表5和表6,不同地震动峰值加速度的加速度、位移及应变峰值试验实测结果与数值计算结果对比误差整理如表9所示。

表7 不同地震动峰值加速度下的数值计算各参数值Table 7 Numerical calculation parameters under different peak acceleration of ground motion地震动峰值加速度(×g)加速度/(×g)位移/mm应变/με0.40.652 4110.608 3601.1710.50.833 1414.322 6730.4120.60.879 6516.852 2829.403
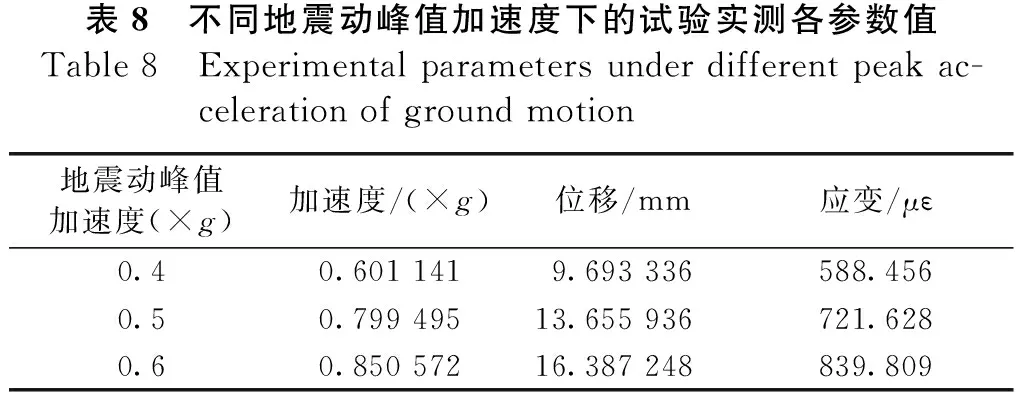
表8 不同地震动峰值加速度下的试验实测各参数值Table 8 Experimental parameters under different peak ac-celeration of ground motion地震动峰值加速度(×g)加速度/(×g)位移/mm应变/με0.40.601 1419.693 336588.4560.50.799 49513.655 936721.6280.60.850 57216.387 248839.809
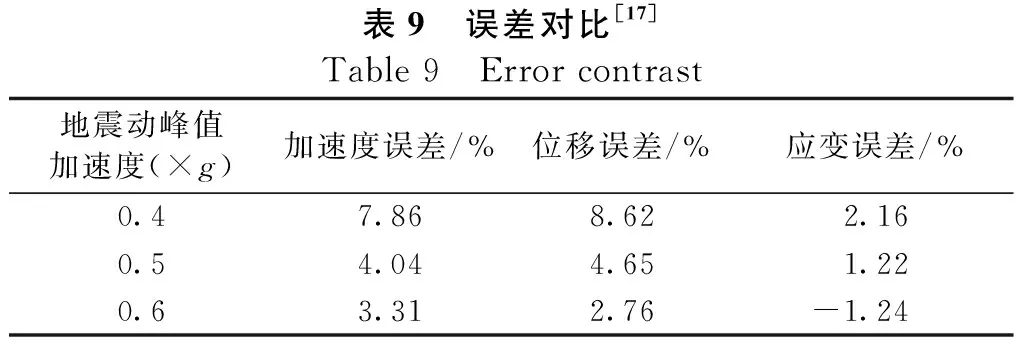
表9 误差对比[17]Table 9 Error contrast地震动峰值加速度(×g)加速度误差/%位移误差/%应变误差/%0.47.868.622.160.54.044.651.220.63.312.76-1.24
分析表7可得:加速度误差较小,都在5%左右;位移误差也都在5%左右,最大也不超过10%;应变误差全都在5%以内。结合3个参数综合分析来看,Goodman单元法向刚度Kn与切向刚度Ks的率定具备较高的准确性。
1.4 有限元模型的建立
依据上文振动台试验介绍利用有限元软件ANSYS建立三维有限元模型,其中模型材料特性的选取要与实际试验的材料统一,该有限元模型的主梁与桥墩均采用Solid185单元进行模拟,密度取2 500 kg/m3,弹性模量取3e11 Pa,泊松比取0.24;桥墩底部全部约束,支座部分用Combin14一维无长度的弹簧单元来模拟。接触部位分别用Targe170单元和Conta174单元模拟目标面和接触面。完整的有限元计算模型及网格划分如图5所示。
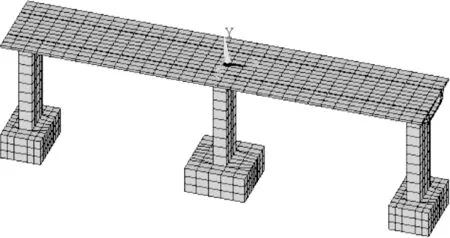
图5 三维整体有限元模型Figure 5 3D integrated finite element model
1.5 地震动的输入
选取符合实际桥梁工程地质条件(Ⅱ类场地)的Elcentro波作为输入地震动,该地震波的加速度时程曲线如图6所示,X向和Y向的加速度峰值均为0.99g,Z向的加速度峰值为0.66g;其持续时间为12 s,X向加速度峰值时刻为t=4.02 s。

(a) X向
2 桥梁结构的接触效应分析
计算桥梁在地震作用下的上部接触部位的位移变化分析桥梁上部结构的接触效应,主要通过提取桥梁模型的位移云图及其时程曲线来实现。使用如图3所示峰值加速度为0.1g的Elcentro波作为输入地震动进行计算,某步时位移云图(第50步、100步、150步、200步)如图7所示,位移及相对位移时程曲线(接触部位)如图8所示。
(a) 第50步
分析图7可得:桥梁与桥墩发生明显的位移差别,桥梁位移较大,桥墩位移较小,一是因为桥墩较桥梁受约束大,二是因为桥梁与桥墩之间设置的支座减少了地震发生时传递给桥墩的荷载,因而产生的位移较小;某时刻桥梁自一跨向另一跨的位移变化逐渐减小,这是由于桥梁受到的地震力不完全一致。
分析图8(a)可得:两个节点发生的水平向位移趋势基本一致,大小有差别,证明两节点之间有相对滑移,不是一致行为;这通过图8(b)可以更直观地看出两节点之间发生相对滑移的大小,在t=4.24 s时相对滑移达到最大,为1.376 mm。从图8(b)中还可以看出相对滑移大小随着时间无明显规律性变化,但在同一地震波作用下相对滑移先增大后减小为零。

(a) 两节点的水平向位移时程
3 桥梁结构接触效应的影响因素分析
基于本文标准模型(地震动峰值加速度为0.1g,混凝土弹性模量为32.5 GPa,接触摩擦系数保持缺省值),通过分别改变各影响参数(地震动峰值加速度、混凝土的弹性模量、接触摩擦系数)以接触面滑移距离(Contact sliding distance)为评价指标分析对桥梁结构的接触效应影响,接触面滑移距离取地震动加速度峰值时刻对应的滑移值,某一参数改变时其它参数保持不变。
3.1 地震动峰值加速度对接触效应的影响
选取地震动峰值加速度为0.1g、0.2g、0.3g、0.4g这4种工况,以接触滑移距离为评价指标分析对桥梁结构的接触效应影响,提取各工况在地震动加速度峰值时刻t=4.02 s的接触滑移值,如表10所示。图9给出了地震动加速度峰值时刻接触面滑移随地震动峰值加速度的变化规律曲线。

表10 各工况的接触滑移值Table 10 Contact sliding distance in each working condition工况地震动峰值加速度(×g)接触滑移距离/mm10.19.70920.214.19930.323.21240.441.488

图9 加速度峰值时刻接触面滑移随地震动峰值加速度变化Figure 9 Variation of contact surface sliding with peak acceleration of ground motion at peak acceleration time
分析表10可得:接触滑移距离随着地震动峰值加速度的增大而增大,这从图9中能更加直观地看出。且从图9中还可以看出:地震动峰值加速度从0.1g增大到0.4g时,3段直线的斜率逐渐增大。可得结论:地震动峰值加速度越大,接触面滑移距离越大,且影响程度越大。
3.2 材料的弹性模量对接触效应的影响
选取混凝土强度等级为C20、C25、C30、C35、C40相对应的弹性模量,以接触滑移距离为评价指标分析对桥梁结构的接触效应影响,提取各工况在地震动加速度峰值时刻t=4.02 s的滑移值,如表11所示。图10给出了地震动加速度峰值时刻接触面滑移随混凝土弹性模量的变化规律曲线。
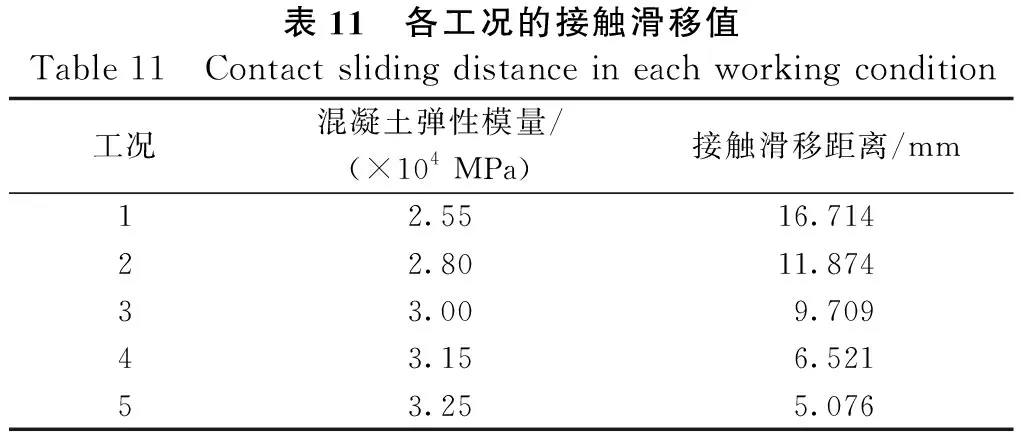
表11 各工况的接触滑移值Table 11 Contact sliding distance in each working condition工况混凝土弹性模量/(×104 MPa)接触滑移距离/mm12.5516.71422.8011.87433.009.70943.156.52153.255.076

图10 加速度峰值时刻接触面滑移随混凝土弹性模量变化Figure 10 Variation of contact surface sliding with elastic modulus of concrete at peak acceleration time
分析表11可得:接触滑移距离随着混凝土弹性模量的增大而减小,这从图10中能更加直观地看出。结合表11和图10中还可以看出:弹性模量从2.55×104MPa增加到3.25×104MPa时,4段直线的斜率变化不大,几乎可以看作是一条斜直线。可得结论:混凝土弹性模量对桥梁接触效应的影响成线性关系。
3.3 接触摩擦系数对接触效应的影响
选取接触面摩擦系数为0.1、0.2、0.3、0.4、0.5、0.6这6种工况,同样以接触滑移距离为评价指标分析对桥梁结构的接触效应影响,提取各工况在地震动加速度峰值时刻t=4.02 s的滑移值,如表12所示。图11给出了地震动加速度峰值时刻接触面滑移随接触摩擦系数的变化规律曲线。
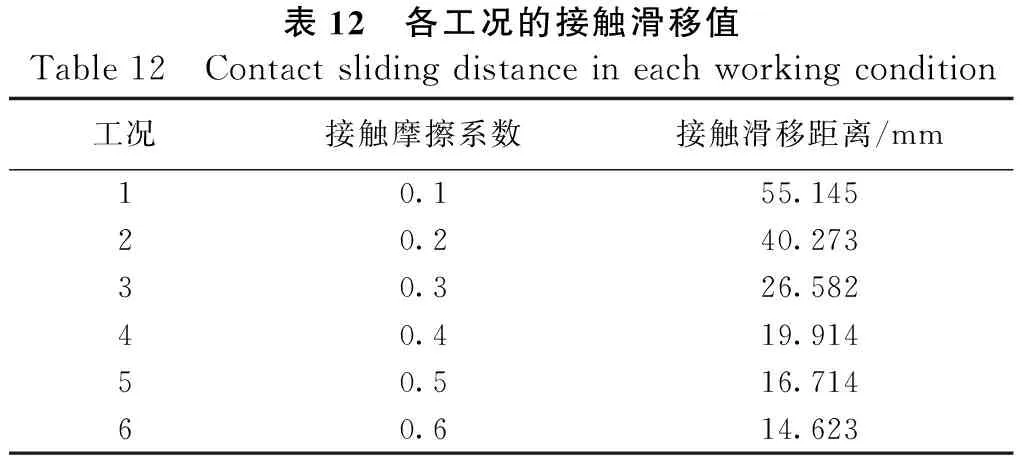
表12 各工况的接触滑移值Table 12 Contact sliding distance in each working condition工况接触摩擦系数接触滑移距离/mm10.155.14520.240.27330.326.58240.419.91450.516.71460.614.623
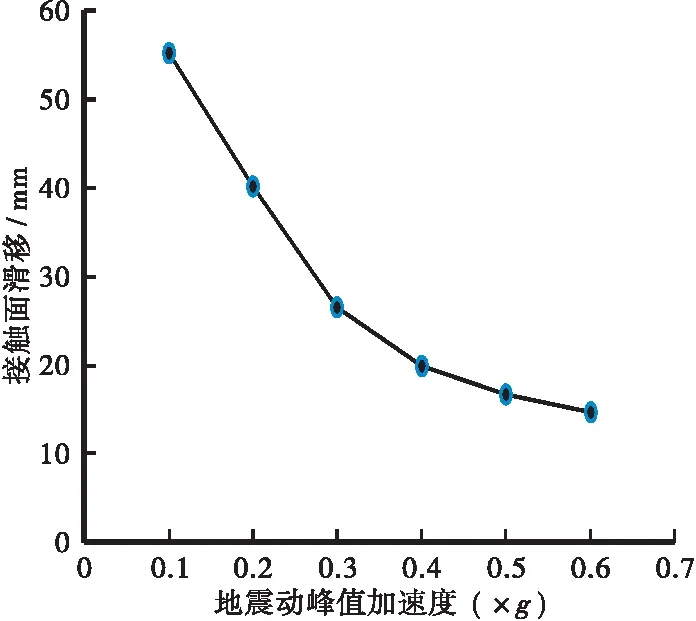
图11 加速度峰值时刻接触面滑移随接触摩擦系数变化Figure 11 Variation of contact surface sliding with contact friction coefficient at peak acceleration time
分析表12可得:接触滑移距离随着接触摩擦系数的增大而减小,这从图11中能更加直观地看出。从图11中还可以看出:接触摩擦系数从0.1~0.6时,5段直线的斜率趋势逐渐平缓。可得结论:接触摩擦系数越大,接触滑移距离越小,且影响程度越小。
4 结论
a.Goodman单元的法向刚度系数率定取试验所用混凝土弹性模量的100倍较为合理;法向刚度系数与切向刚度系数关系式为:Kn=2.48Ks。
b.接触部位两节点位置在同一地震波作用下会发生明显的相对滑移,且总体趋势为先增大后减小为零,在t=4.24 s时达到最大;其大小随着时间变化无明显规律。
c.接触面滑移距离随着地震动峰值加速度的增大而增大,且影响程度也增大;接触面滑移距离随着混凝土弹性模量增大而减小,但影响程度变化不大,可以看作是线性关系;接触面滑移距离随着接触摩擦系数的增大而减小,且影响程度也减小。

