基于激光视觉的分瓣形封头坡口自动分层切削方法
刘源泂,宋 建,袁文新,薛海浪
(1.武汉科技大学 冶金装备及其控制教育部重点实验室,武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室,武汉 430081;3.宜兴市九洲封头锻造有限公司,江苏宜兴 214212)
0 引言
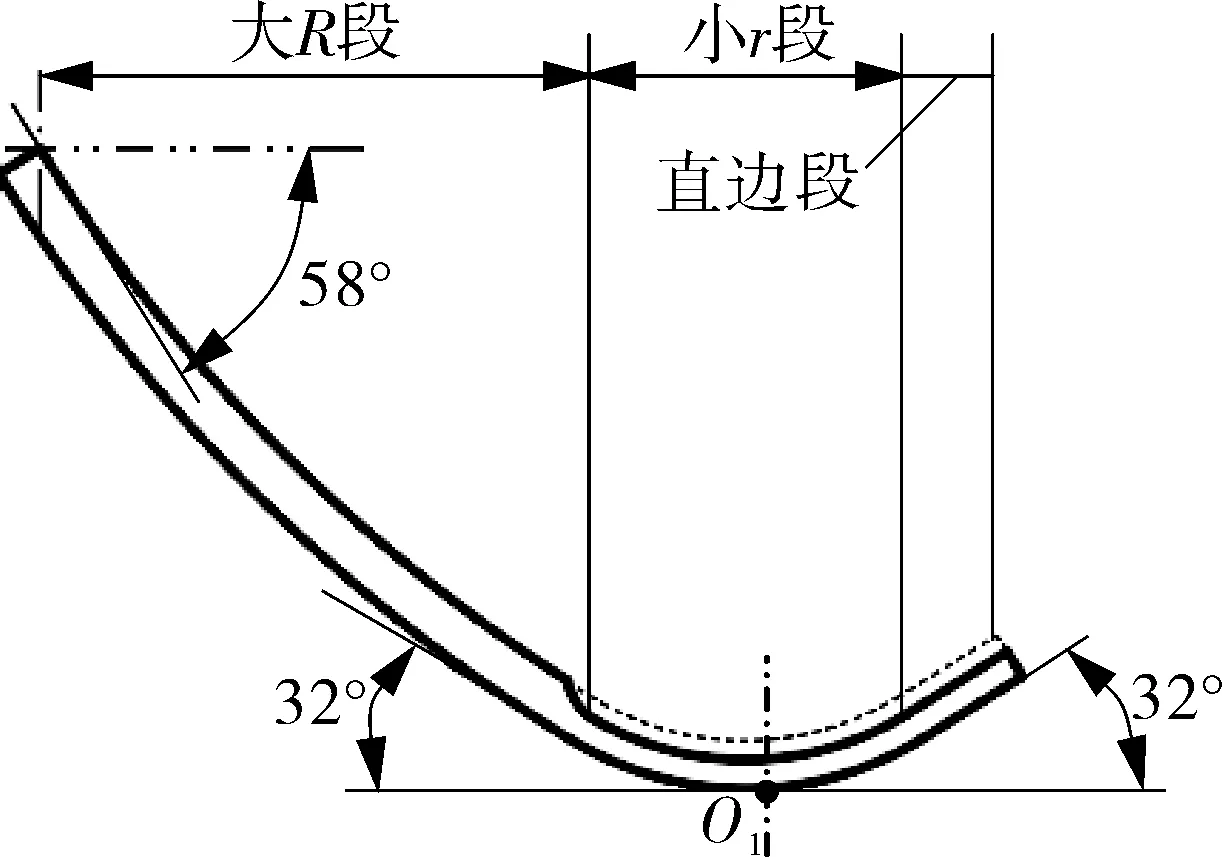
分瓣形封头[1-2]是由顶圆板、多个瓣片冲压组焊成形的一种大尺寸变曲率曲面的工件,是压力容器的重要组成部分,广泛应用于能源化工等领域。分瓣形封头有防腐等特种要求时要采用复合板材质,复合板一般由基层和覆层两层材料组成[3-4]。如图1(a)所示,对分瓣形碟形封头组装焊接时,由于材质焊接性质不同,需先去掉瓣片对接焊缝处的覆层,露出基层(图1(b)切削部分1),再开坡口(图1(b)切削部分2,3)形成对接焊缝[5-6]。目前该类封头分层切削采用人工打磨或盘铣床铣削去掉覆层等方式,存在打磨碎屑、噪声污染等问题,且铣削时需人工实时观察并调整刀具高度,劳动强度大、加工效率低。因此,提高该类变曲率工件表面分层加工的自动化程度具有重要应用价值。

(a)分瓣形碟形封头结构

(b)瓣片轴向坡口加工图
采用激光三角法的线结构光视觉测量构架,具有结构简单、非接触、响应快等优点[7],广泛用于缺陷检测[8]、精密测量[9]、三维重建[10]等方面。常用的光路构架包括单线、双线及多线结构光[11-14],其中双线结构光方案兼顾了测量视野、灵活性及算法效率。如实时检测双线间距反馈焊缝高度变化,实现自动调节焊枪高度[15];基于双线结构光测量模型实现大型卫星对接环捕获姿态测量[16];配合双目视觉点云频域配准算法,利用双线结构光实现列车轮对检测[17]。本文针对分瓣形封头瓣片轴向坡口(见图1(a))定深度铣削工况,构建变曲率下双线结构光与刀具铣削深度测量模型,将两个线激光器和一个面阵相机搭建成激光视觉系统,并与盘铣刀的轴心相对位姿固结(见图2),设计标定算法实现精确求解位姿关系,搭建曲率表面测量实验台,分析切削倾角变化、切削步长及铣削精度关系,提出一种分瓣形封头的变曲率表面自动分层加工方法。

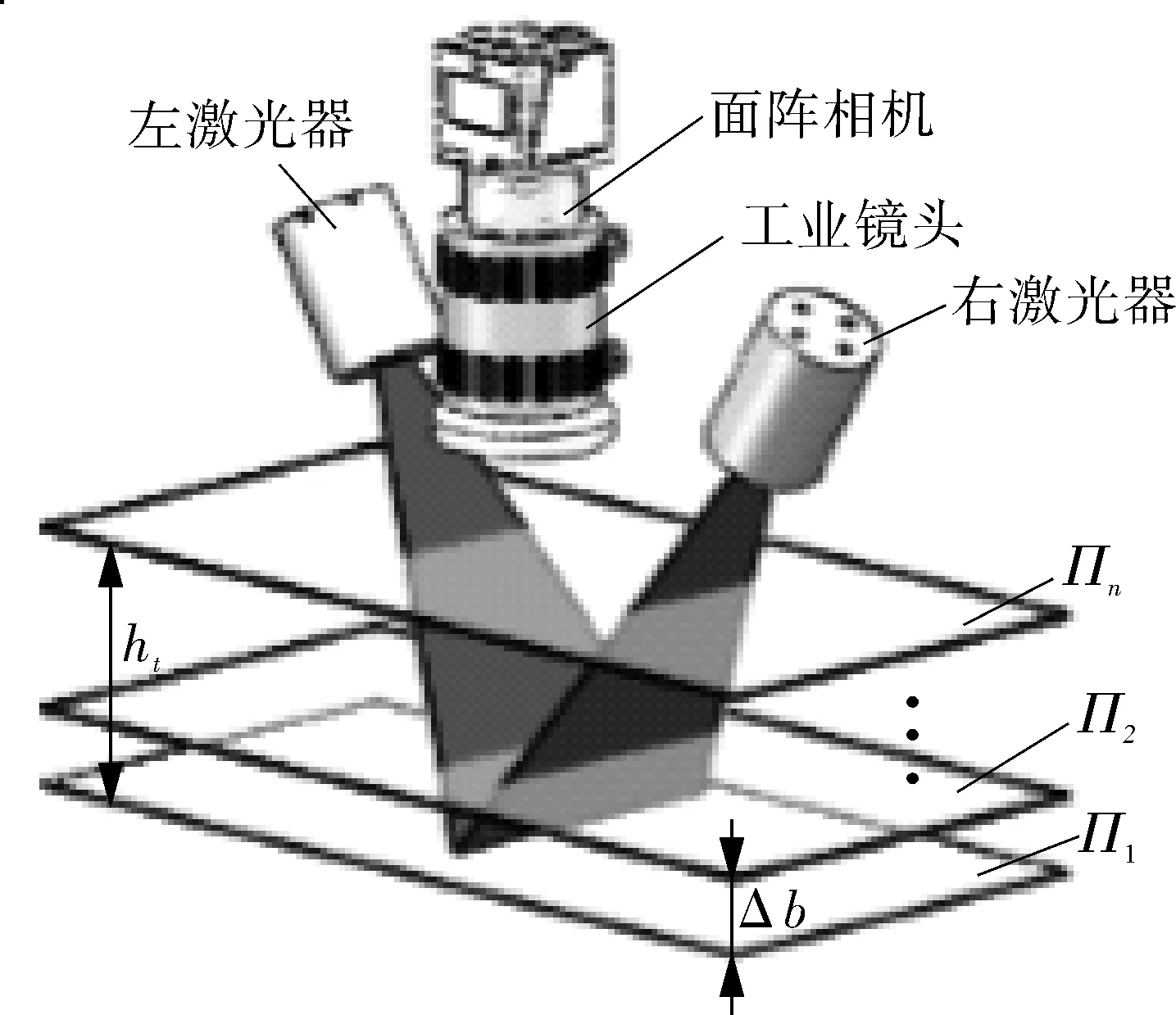
图2 激光视觉系统结构
1 曲面深度信息提取原理
1.1 激光视觉系统结构
激光视觉系统由两个线激光器、面阵相机、镜头及角度调节座等组成,如图2所示。视觉系统检测点位于铣刀切削点一侧,两激光器与竖直方向夹角分别为β1和β2(见图3)且对称安装于相机两侧,相机视场内两激光线相互平行,两激光线共线时与图像中心重合。

图3 曲面切削深度信息提取模型
1.2 变曲率表面切削深度测量模型
1.2.1 曲面切削深度信息提取模型
d=hcosθ
(1)
其中:
(2)
(3)
式中Ll——AB的像素距离;
Lr——BC的像素距离;
ye——当前位置的系统空间分辨率,mm/pixel。
1.2.2 刀具切削过程分析
刀具切削过程如图4所示。刀具的切削增量(进给量)为Δh;T和T1是刀具在竖直方向上的切削起点;B和B1是刀具在竖直方向上切削终止点;θ1和θ2分别是切削点M和M1处的切削倾角。刀具先由T点到B点,h1为TB处的竖直切削深度,其中h1=TB,当达到要求切削深度后,曲面工件沿X轴负半轴方向移动一个步长s,进入T1B1位置切削,h2为刀具由TB位置运动到T1B1位置处后刀具的竖直切削深度,其中h2=T1B1,he和de分别为刀具任意位置的竖直切削深度和法向切削深度,ht为刀具竖直方向待切削深度,dt为法向待切削深度。
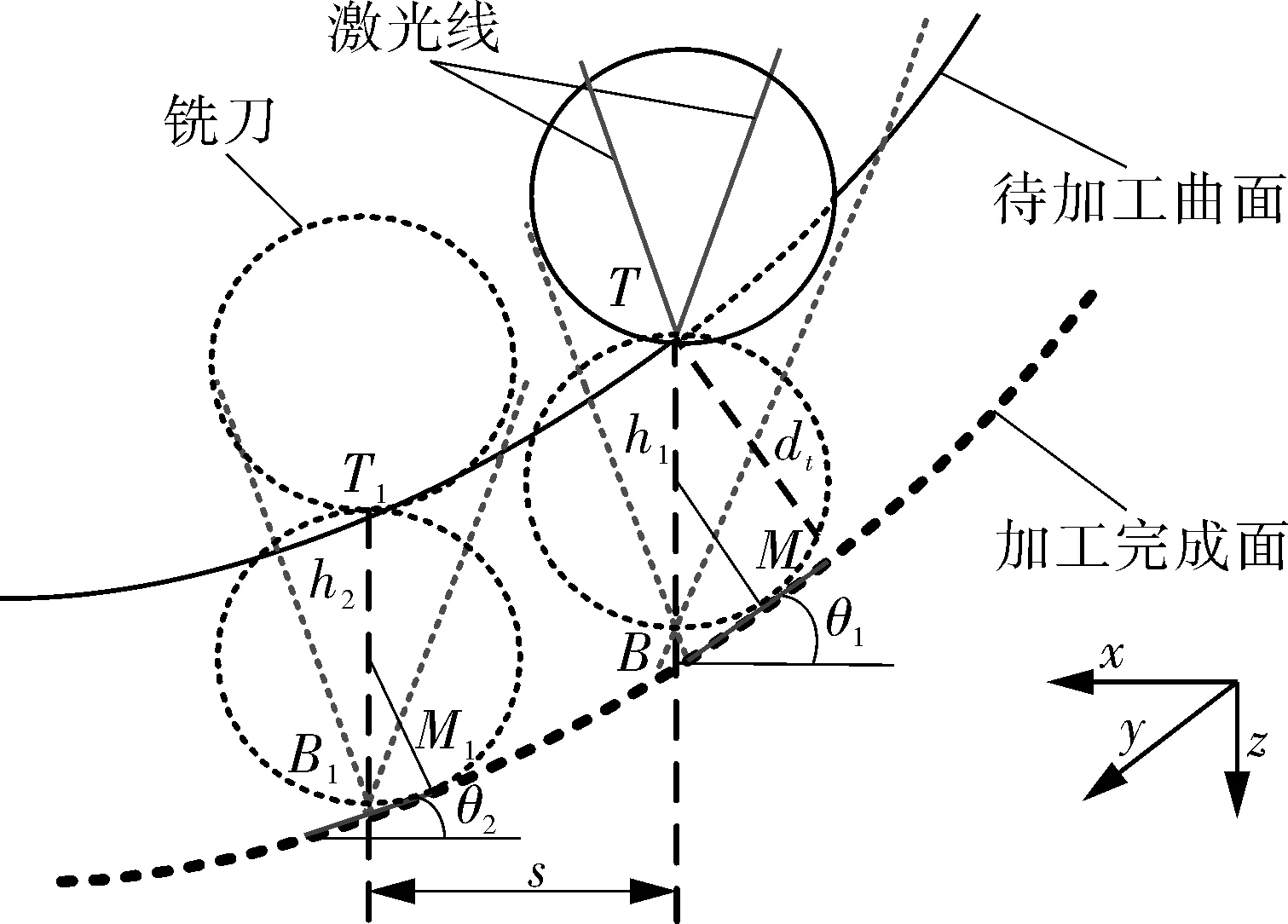
图4 连续切削过程示意
通过数学模型计算刀具运动到B处的高度h1(L1与L2是TB处的光条纹间距):
(4)

(5)
由式(1)(2)可得:
(6)
判断de与dt的关系,若de 双线结构光测量实验平台(如图5所示)包括2个高精度直线模组①⑨,1个角度调节器⑧,2个角度旋转平台④⑦,1个面阵相机②,1个工业镜头⑤,2个线激光器③⑥,变曲率表面工件⑩,实验架。2个高精度直线模组用于模拟刀具的切削运动和曲面工件的进给;2个角度旋转平台用于调节激光器的入射角度;面阵相机用于捕获线激光图像信息;2个线激光器用于向曲面投射线结构光;角度调节器调节曲面工件的倾斜角度。 图5 双线结构光测量实验平台 线结构光视觉系统标定[18-20]分为相机标定、双线结构光标定、激光条纹中心提取。本文采用张正友标定法[21]完成图像畸变矫正和标定平面外参矩阵的获取。相机标定完成后,通过式(7)空间坐标系中的特征点和图像坐标系中像素点的对应关系式,可获取任意像素点的空间坐标。 (7) 双线结构光标定分为双线视场中心标定、空间分辨率标定和激光入射角标定。标定原理如图6所示,由高精度模组调节待标定面的间距Δb,ht为刀具竖直方向上设定的切削深度(即需要标定的深度),ht=nΔb(n∈Z),Πn(n∈Z)为待标定平面。 图6 线结构光测量系统标定 2.2.1 双线视场中心标定 固结激光视觉传感器,拍摄一幅双线光条纹完全重合的图像作为基准图像,默认基准图像中光条纹重合时的位置为此标定系统拍摄的双线光条纹图像的中心线。设图像的大小为(M,N),利用Steger法[22]提取光条纹中心并计算光条纹重合中心的纵坐标MC与相机视场中心(图像中心)的纵坐标MV,并计算其差值Δb=∣MV-MC∣,双线视场中心标定结果如图7所示。 图7 双线视场中心标定 2.2.2 空间分辨率标定 在刀具切削过程中,随着物距的改变双线结构光条纹的空间分辨率在一定范围内也发生了改变,但满足小孔成像原理。 (8) 式中S——图像传感器单位物理尺寸,mm/pixel; a——像素坐标系中双线结构光条纹间距,pixel; A——空间中双线结构光条纹间距,mm; f——相机标定后的焦距,mm; u——相机标定后的物距,mm; he——刀具竖直切削深度,mm。 对式(8)变形可得: (9) 利用高精度模组调节不同的切削增量完成切削模拟,利用式(7)(9)计算不同切削深度处的空间分辨率,为了降低试验误差的影响,用最小二乘法拟合出空间分辨率和切削深度的关系式ye=-0.0009027he+0.0559(ye为任意竖直切削深度he对应的空间分辨率),拟合结果见图8。 图8 切削增量与空间分辨率拟合线 2.2.3 激光入射角标定 调整2个线激光器支座,使标定平面上的两激光条纹平行,且双线重合时与图像中心重合,设定线激光的入射角为30°后,紧固线激光器支座的粗调旋钮,模组调节待标定面至不同的竖直切削深度he,对双线结构光条纹成像,利用改进灰度重心法提取光条纹中心,并计算条纹间距(图3中AB,BC),由下式计算左右激光入射角β1和β2: (10) 线激光入射角标定结果如表1所示。 表1 线激光的入射角度标定结果 线结构光条纹中心提取是线结构光视觉测量中的一个关键技术。常见的光条纹提取方法有方向模板法[23]、Steger法、灰度重心法[24]。由于方向模板法在精确提取光条纹中心时需要增加模板数量;Steger法则需要消耗较多的计算时间,因此这两种方法都不适合光条纹中心的在线快速提取。灰度重心法是以能量提取法为基础的光条纹提取算法,根据光条纹在每一行横截面区间内灰度值的排列,计算该截面的光条纹灰度重心并将其作为当前行的激光条纹的中心,但传统灰度重心法易受噪声影响,条纹提取精度较低。本文利用改进灰度重心法提取光条纹有效区域内光条纹的中心,满足提取精度要求且能实时在线提取,具体算法实现如下。 2.3.1 图像预处理 利用双线视场中心标定的条纹中心Mc将双线结构光条纹分割为单线结构光条纹,随后对单条纹图像进行灰度化处理,利用灰度邻域属性法[25-26]提取光条纹中心,沿着光条纹延伸的方向从光条纹中心向两端各取13个像素作为光条纹的有效区域,采用中值滤波对光条纹的有效区域进行降噪,结果如图9所示。 图9 光条纹预处理结果 2.3.2 光条纹中心提取 设需处理的图像大小为(M,N),其中某个像素的大小为I(i,j),左线单条纹每行的中心点为Pl(ilc,jlc),右线单条纹每行的中心点为Pr(irc,jrc)。 (1)计算有效区域内线结构光条纹每一行的灰度重心坐标,记Glj(xlj,yj)为左线结构光条纹每一行的灰度重心点,Grj(xrj,yj)为右线结构光条纹每一行的灰度重心点。 (11) (12) 式中xlj——左边光条纹的第j行灰度重心纵坐标; xrj——右边光条纹的第j行灰度重心纵坐标。 (13) (14) (3)计算双线结构光条纹的距离。 (15) 可得: (16) 式中L1——左边结构光条纹到中心线的距离; L2——右边结构光条纹到中心线的距离。 双线结构光条纹中心提取结果如图10所示。 图10 双线结构光条纹中心提取结果 步长S是刀具切削过程中一个重要参数。适宜的步长可以满足不同位置处曲面工件的切削要求,过大则引起光条纹失真;过小则影响加工时效性。将连续变化的曲面切削倾角θ离散为0°,10°,20°,30°的斜面(平面)进行试验。由刀具的切削倾角θ,竖直方向切削深度高度he,空间分辨率ye,以及激光入射角β1和β2,可得光条纹分离误差率δ的计算公式。 (17) (18) (19) 式中LC1——左线光条纹分离距离; LC2——右线光条纹分离距离; Lc——双线光条纹的实际分离距离; La——算法计算的双线光条纹距离; δ——光条纹分离误差率。 试验通过比较不同的步长S和光条纹分离误差率δ的关系,寻找不同角度下的合适步长S,结果如图11所示。 图11 变曲率下条纹间距提取值与理论值的误差率 切削0°~20°斜面(平面)时,随着步长增加,双线光条纹的间距提取误差率逐渐降低,对于0°~10°斜面(平面),当步长达到8 mm后,误差率开始上升,选择7 mm左右的步长可以保证条纹间距提取误差率1%左右;对于20°斜面,当步长达到4 mm后,误差率开始上升,选择用4 mm左右的步长可以保证条纹间距提取误差率为4%左右;切削30°斜面(平面)时,随着步长增加,双线光条纹的误差率逐渐增加,选择1.5 mm左右的步长可以保证条纹间距提取误差率为5%左右;当曲面切削深度为3~10 mm时,光条纹提取误差为0.025 9~0.375 mm,满足工件加工要求;对于0°,10°,20°的斜面(平面),当切削增量为1~3 mm时会有较大的误差,这是由于受到图像处理算法和视觉硬件的限制,导致双线光条纹发生近距离散射,致使光条纹提取精度较低,针对这种情况,采用较大的切削增量即可保证曲面加工精度。 将连续变化的曲面切削倾角θ离散为0°,10°,20°,30°斜面(平面),并将其作为试验斜面的理论倾角θt,算法计算的倾角记为θa,ε为误差角。将标定后的β1和β2代入式(2)可得: (20) ε=∣θa-θt∣ (21) 调节不同的切削增量Δh对理论倾角为θ的斜面进行切削,通过以上公式计算θa,ε,分析算法误差角ε,以验证切削倾角计算的可靠性,结果如图12所示。 图12 切削倾角误差计算结果 采用相同切削增量Δh进行切削时,ε随着θ的增大而增大,30°斜面的最小切削倾角误差为3.4°,最大倾角误差为8°,由倾角误差造成的切削误差为0.084~0.61 mm;采用不同的切削增量Δh进行切削时,随着刀具切削增量的增加,误差角也逐渐增加。由于受到噪声的影响,当斜面倾角为20°,切削增量Δh=1 mm时,ε发生了异常,但是总体上,ε随着Δh增大而增大,对于异常情况,通常采用多帧图像平均的方法即可消除。合理地选择刀具的切削增量能够有效地控制误差角,保证切削精度。 文中提出的基于激光视觉的曲面工件自动定深度切削方法,通过试验表明该方法对一定曲率变化率较小(对应切削倾角±30°)的曲面,测量的最大切削倾角误差为8°,加工误差在5%以内;切削深度为3~10 mm时,步长变化引起的条纹提取误差为0.025 9~0.375 mm,最大切削倾角误差引起的切削误差为0.084~0.61 mm,满足分瓣形封头的加工要求。对于常见的分瓣形球形封头、分瓣形椭圆形封头以及分瓣形碟形封头,在允许刀具切削的范围内,通过调整变曲率工件(单瓣)的装夹位姿来调节其最大切削倾角,以满足文中所提出的加工倾角范围要求。其中,对于分瓣形碟形封头瓣片存在的小r处(曲率变化大),通过调整瓣片在加工过程中的位姿,可将其最大切削倾角调整为32°,如图13所示。结合图12可知,采用较小步长即可完成小r处的加工。 (a)小r段和直边段 (b)大R段 本文方法较传统分瓣形封头的加工方式具有较高的精度和效率,并替代人工,提升自动化程度。2 曲面切削实验平台搭建
2.1 实验平台简介

2.2 双线结构光视觉系统标定

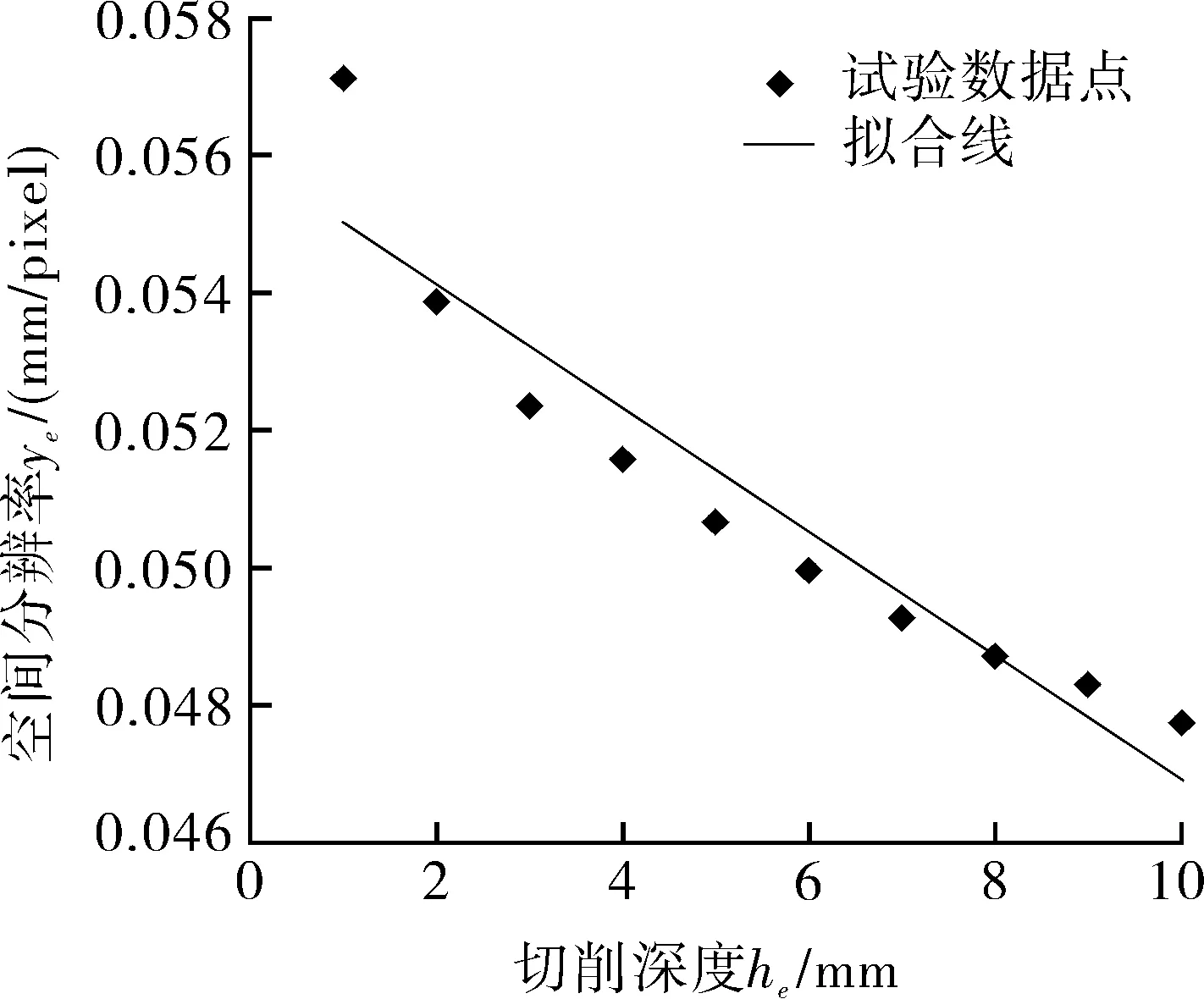
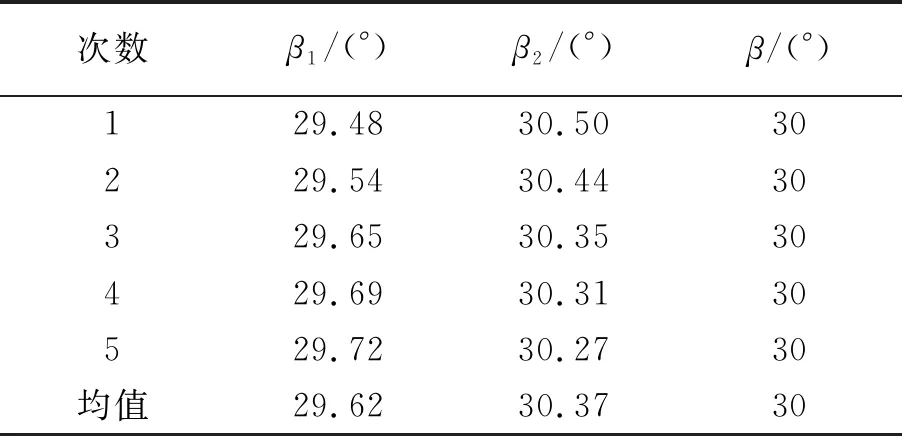
2.3 激光条纹中心提取


3 结果分析
3.1 光条纹提取精度
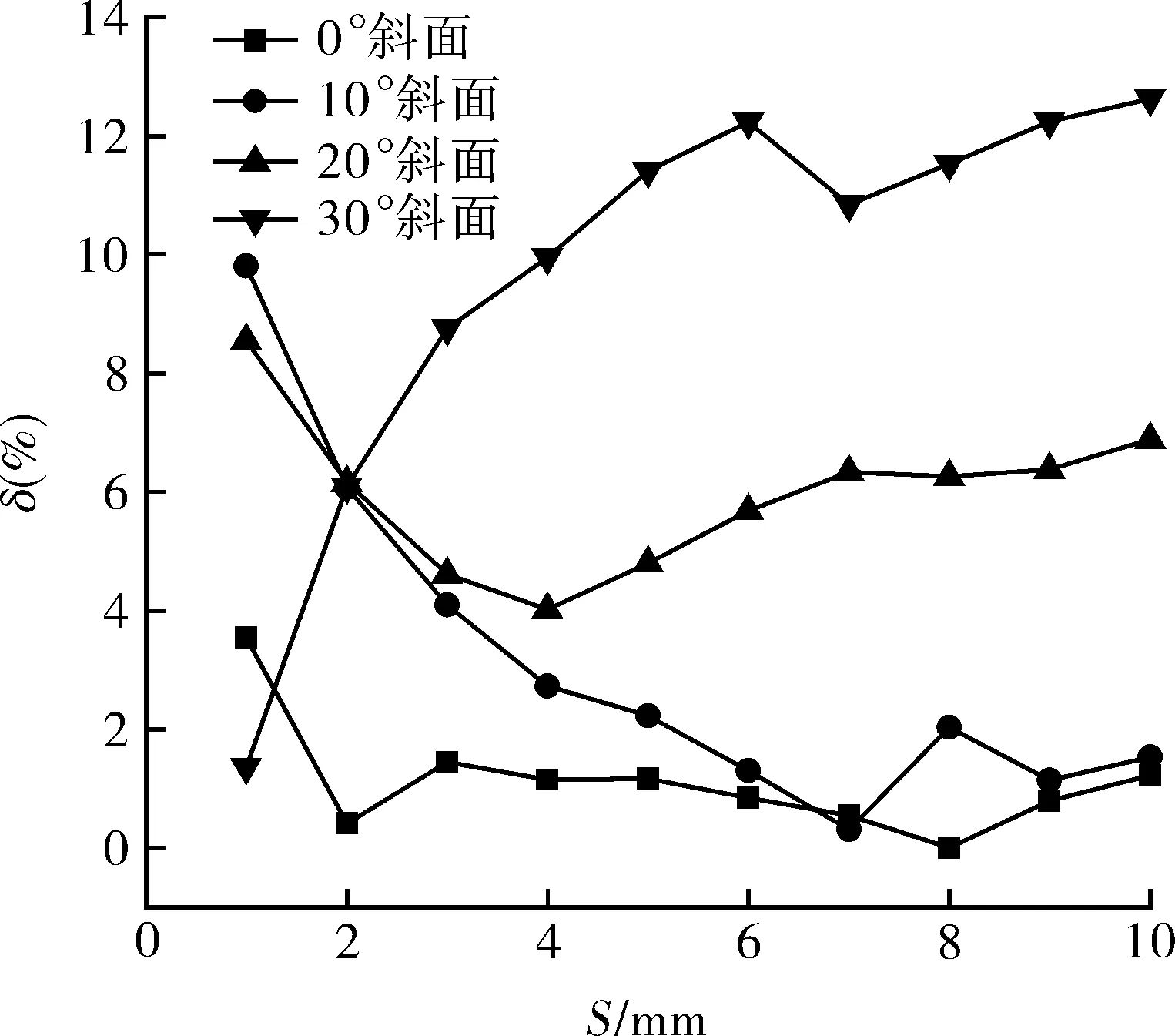
3.2 切削倾角测量精度

4 结语