关节臂式测量机动态误差分析与补偿

李少芝，杨凯

（马鞍山市特种设备监督检验中心，安徽马鞍山243000）

0 引言

三坐标测量机因精度高、环境适用性好，广泛应用于汽车装配、机械加工制造、精密仪器检测等领域。但随着智能制造的发展和工业生产加工过程中对精度、实时性及机动性需求的不断提高，三坐标测量机的发展受到了制约。关节臂式坐标测量机（Articulated Arm Coordinate Measuring Machine，AACMM）因其机械结构简单、体积小、重量轻、运行效率高、可测范围广、能够进行现场测量等优势，成为了新的研究重点。关节臂测量机通常具有6自由度，采用非笛卡尔坐标系［1］实现空间内的广域测量，通过类似关节机器人的串联式空间开链式连杆机构［2］模拟人体手臂进行工作。受结构影响，该种测量机在工作过程中会产生误差的逐级累积、传递、放大的问题，影响最终测量准确度。其静态参数误差主要为所选用模型内的结构参数误差，属于模型本身的固有误差，通常为定值，可通过自标定法或外部标定法进行校准［3-4］。而对于关节臂测量机动态误差补偿的理论研究由于其本身参数的多样性与过程的复杂性，成为了国内外学者研究的重点。

胡毅［5］等人针对温度因素，建立了基于神经网络的热变形误差修正模型，实现了对温度影响的量化补偿。于浩［6］等人针对关节臂测量机在齿轮方面的应用，分析了关节臂从测头到基座的坐标传递模型，并讨论了测量平台与被测工件之间的位姿关系。朱嘉奇［7］等人针对柔性臂坐标测量机误差溯源及不同误差之间呈现非线性化的问题，提出将模拟退火融入BP神经网络的方法，实现了对动态误差的补偿。

文章在众多学者的研究基础上，进一步分析关节臂坐标测量机各误差的来源，对测量过程中动态误差部分相关参数进行研究，并提出一种模糊神经网络（Fuzzy Neural Network，FNN）与模拟退火算法相结合的误差补偿方法，通过与补偿前的实验数据进行对比，论证该方法的可行性。

1 关节臂测量机误差来源及分析

1.1 测量机工作原理

关节臂式测量机由3个关节臂和1个测头通过6个旋转关节组合而成［8］，其结构如图1所示。

图1 关节臂式测量机结构图

本研究采用接触式测头，由牵拉测量机测头联动整个测臂的移动，通过测量关节的转角获得被测点的三维坐标，以角度测量基准取代长度基准，从而建立完整的测量空间系统。

1.2 测量误差来源及分析

由于关节臂测量机结构上可动点较多，整个关节臂的运动包含旋转、定轴转动等，有些型号还包括受力较复杂的管壁活塞运动，因此测量机的误差来源也复杂且广泛。目前研究认为对测量结果影响较大的误差主要分为［8］：

1）测量系统固有误差

测量系统固有误差包括由于设备的结构件参数在生产制造过程中与真实值存在一定偏差而引起的结构参数误差，以及工作过程中测臂自身重量导致测头发生少许位移而产生的力变形误差。

2）测量过程环境误差

测量过程环境误差主要包括由于外界温度变化引起测量机测头、测臂、圆光栅等关键部件受热产生的热变形误差，在精度要求更高的场合，还包括由于湿度变化导致的测量误差。

3）测量过程动态误差

测量过程动态误差包括测量力误差（即由于测量过程中测头与被测物体接触所产生的测头或测臂形变导致的误差）、测头系统误差及角度编码误差，其中角度编码误差中最重要的误差来源是关节角度传感器的安装偏心误差［8］。

4）测量随机误差

随机误差在测量过程中总会出现，可以通过多次重复测量减小其影响。如运动误差、数据采集误差等。

1.3 测量机数据传递建模

针对系统固有的静态误差，可以通过D-H模型［9］配合标定法对其进行控制。在单点固定站位的测量中，定义σs为末端传感器坐标系，σp为测头基准坐标系，σT为测臂工具坐标系，σBM为底座基准坐标系，四个坐标系的坐标变换构成了整个关节臂的位姿调整环节，如图2所示。

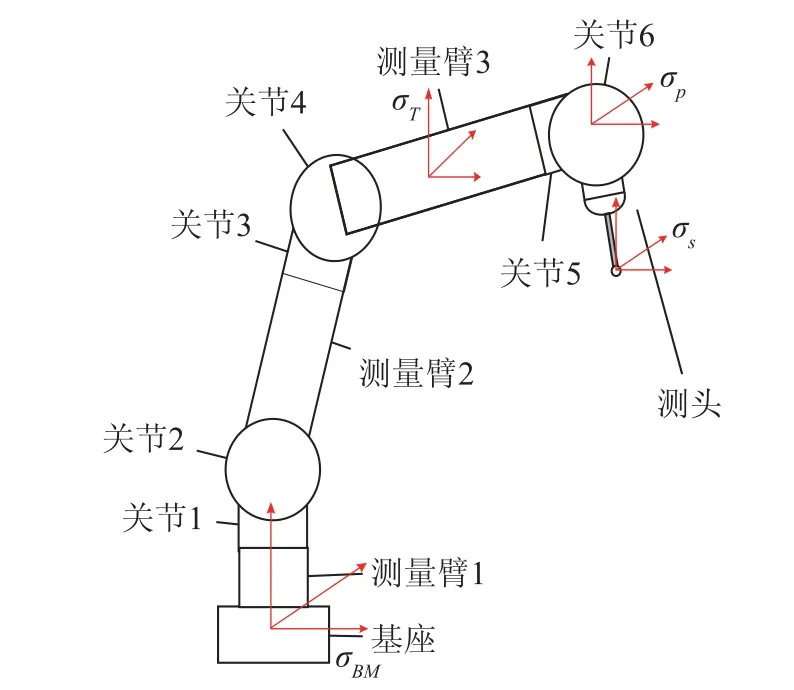
图2 固定站点数据传递模型

关节臂测量机各部分之间的位姿关系均可由其坐标系与基准坐标系σBM之间的平移与旋转来表示，即相差一个转移矩阵

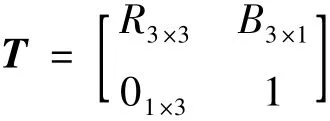
该矩阵表示坐标由N到M的转换。其中，R为旋转量，B为平移量。

对于传感器坐标系σs测得的数据点P0=（x0y0z0）进行上述位姿调整之后，在底座基准坐标系σBM下的点就转换为

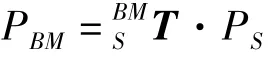
式中：PBM和PS分别为坐标系σBM和σs下的点坐标；为两坐标系间的转移矩阵。

此时，测头传感器到测量机基座之间的数据传递过程建立为一种理想的数学模型，静态测量误差得到了有效补偿。但是考虑到测量过程的复杂性，动态误差使用这种方式补偿显然是不合适的。针对关节臂式测量机动态误差，选取热变形误差、测量力误差与角度编码误差三个最主要的影响因素进行分析。

1.4 动态误差补偿预实验

环境温度是影响测量准确度的一个重要因素，由于关节臂式测量机的活动点较多且相互间没有更多的支撑，因此相较于传统的测量机，其测量结果更容易受到温度变化的影响。在研究测量力误差与角度编码误差这两个核心因素之前，通过实验分析确定最理想的测量环境，使热变形误差的影响降到最低。

在进行温度变化预实验时，选取固定长度作为对象，以0℃为起点，1℃为测温步长，记录0～40℃范围内的测量误差变化曲线。每个温度值点都选取100个测量值，取平均记为L′，真实值记为L，则该点误差为误差曲线如图3所示。

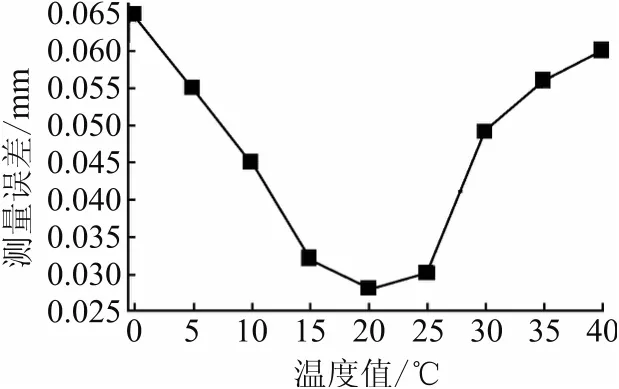
图3 热变形误差曲线图

从图3中可以看出，热变形误差在约20℃时为明显极小值点，低于或高于20℃时均单调变化，因此20℃是此关节臂式测量机的理想工作温度。

后续实验中，为使关节臂测量机在理想温度环境下工作，在其6个活动点处安装温度传感器，由四个恒温出风口对关节臂进行加热恒温，使其温度保持为20℃。且所有实验均在精密实验室内进行，所有仪器使用前均经过标准预热。

2 模糊神经网络与模拟退火算法

模糊理论与神经网络相结合诞生了模糊神经网络（Fuzzy Neural Network，FNN），即采用神经网络结构实现模糊理论的功能，将二者的优势相互融合且达到互补。单一模糊系统难以表示明确特征量，如学习、信息处理、视觉识别等，而通过模糊神经网络则可以解决此问题［10-11］。

Takagi-Sugeno（T-S）模糊神经网络采用了融合神经网络与模糊推理的独特结构。成功实现了模糊理论中模糊规则的自动生成，能够在自动调整模糊隶属度函数的同时，通过神经网络的部分实现原本不具备的大规模运算能力以及自学习能力［12-16］。

在非线性动力学中引入T-S模糊神经网络是解决测量准确度问题的重要方法之一，而关节臂式测量机动态误差由动力学引起，具备高度复杂的非线性特征，因此，T-S模糊神经网络适用于关节臂测量机动态误差的模型建立。

2.1 T-S网络动态误差补偿模型输入量分析

设计模拟神经网络模型时，需要先对测量力误差与角度编码误差的影响因素进行分类，从众多因素中筛选出最主要的因素作为补偿模型的输入量。

对于测量力误差而言，测头从起始处移动至被测物体的运动过程是测头产生形变的最大误差来源。在此过程中测头先加速达到最高速度点，再减速到达被测物体，最终与物体接触。为了方便分析接触力的大小，将整个运动过程与测头的受力大小建立联系，利用测头运动的最大定位误差（MPE）和残余定位误差（RPE）表征测头受到并使之产生形变的力的大小，MPE与RPE越小，测头定位越准确，物体对测头施加的力也就越小，产生形变也相应较小。

影响关节臂测量机角度编码误差的因素通过6个关节转角值（JA）来表征［7］。

2.2 T-S网络动态误差补偿模型结构设计

T-S模糊神经网络的输入量模糊划分决定了系统的复杂程度，过多的划分会使得学习时间呈指数型增长。根据实际需要，本文将影响结果的最简化8个动态参数构造T-S网络模型，其结构如图4所示。其中，P为各后件网络输入节点；μ为对应模糊分量的隶属度；α为前件网络中与层各节点；y为后件网络中m个独立节点的模糊规则。

图4 T-S动态误差网络模型

1）前件网络设计

前件网络共分为四层：输入层、隶属度层、“与”层和归一化层。其中，输入层将8个动态误差因子输入量X=［x1，x2，x3，x4，x5，x6，x7，x8］传给隶属度层，故包含8个输入节点；隶属度层接收到输入变量后，按照模糊规则对其进行模糊化，并同时赋给每个模糊分量相应的隶属度函数值，对于本文的8个输入维度，设计3个模糊分割层次，即负、零、正，使用高斯函数赋予隶属度值，因此本层的节点数应为N2=3×8=24；“与”层的功能是计算模糊规则的隶属度，其节点数应与设计的模糊规则总数相等，为N3=m=∏i=1mi=38=6561；最终通过归一化层加快训练网络的收敛性得到前件输出，其节点数N4=6561与前层相等。

2）后件网络设计

后件网络由三层构成，其中8个影响因子加上一个为模糊后件提供常数项的x0=1共同构成第一层，即后件网络的输入层。输入变量通过输入层传递给第二层计算模糊规则下的后件。该层中每个节点都表示一个独立的模糊规则，共计m个节点，即

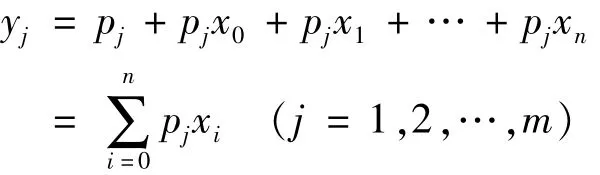
将第二层的计算结果传递给第三层输出层，同时引入前件网络的计算结果作为该各项规则后件的加权系数，该系数称为模糊规则的激活度，因此整个网络的输出为各项规则后件的加权和y为

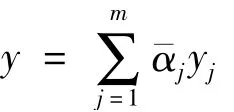
对需要辨识的后件网络连接权值pj，模糊隶属度函数的中心值cij以及宽度σij（j=1，2，…，6561；i=1，2，…，8）三个参数进行算法设计。

算法中误差函数取为

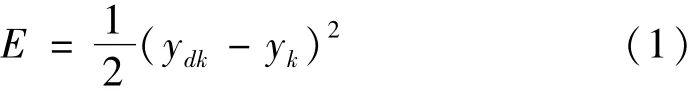
式中：ydk为期望输出；yk为实际输出。

具体参数辨识步骤如下：

①为三个辨识参数pj，cij，σij随机赋起始值。

②对训练样本数据按照如下方式进行迭代：

式中：β为训练模型的学习率；k为迭代次数；t为迭代的当前值。

③当训练结果单组数据的误差小于预设误差时，则误差准确度达到了要求，停止该组数据的迭代训练，否则继续进行。

④误差准确度达标的实验组，停止迭代。转入②将下一组训练样本继续迭代，直至整组样本集完成训练。

2.3 融合模拟退火算法优化的T-S模糊网络模型

模拟退火（Simulated Annealing，SA）算法起源于蒙特卡洛算法，并于1953年由Metropolis等人提出，是一种主要应用于大空间中寻找最优解的概率算法。传统的爬山算法也能够快速地寻找临近解的极大值，但当遇到函数极大值非最大值点时，爬山算法对比极值点两端数据大小之后，极易将该点误认为最大值点，从而陷入局部最优的僵局。而SA算法在局部寻优的基础上随机性地加入一定扰动，有一定几率让这个局部最优解跳出局部解空间，从而继续对全局最优解进行搜寻，在多次于函数最值周围振荡徘徊后，最终确定该最值点为函数的全局最优解，可巧妙避开局部最优的陷阱。

给定初始温度T0，令初始最优解w*=w0，根据干扰产生的新解为wβ，可通过ΔE=E（wβ）-E［w（k）］求优化函数指标。接受判定的条件为：①若ΔE≥0，计算接受概率r=exp［-ΔE/T］，若r＞pp，则w（k+1）=wβ，否则w（k+1）=w（k），pp为区间［0，1］上的随机数；②如果ΔE＜0，则w（k+1）=wβ，w*=wβ。每次过程令k=k+1，如果k大于设定值N，则开始降温，最终当达到预设检验误差范围内或者预设终止温度时，输出当前值w*作为最终最优权阈值。融合SA算法的网络基本步骤如图5所示。

设计算法补偿过程中的各连接点权值Pj时，通过模拟退火算法找到神经网络权阈值的全局最优解，利用突跳特性避免陷入局部极小值的问题，使得网络输出更好的逼近真实值，提高神经网络的预测准确度。

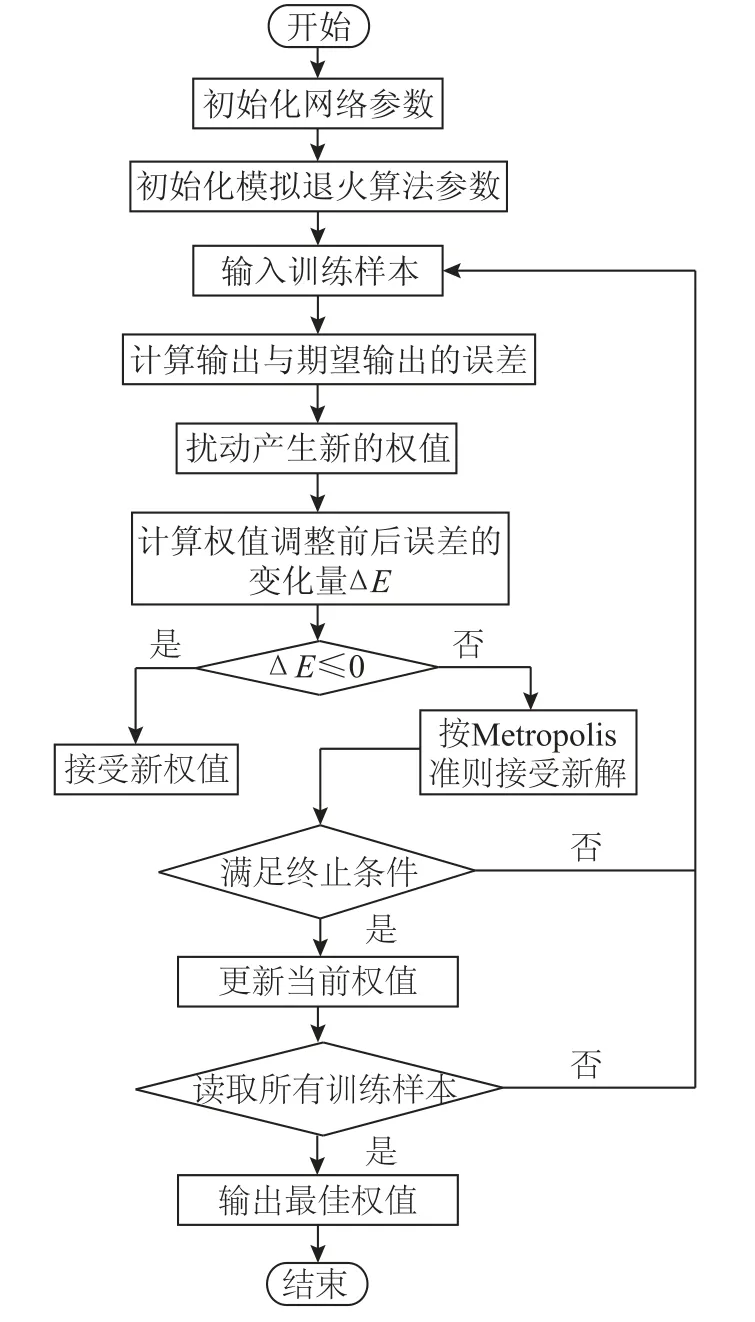
图5 模拟退火算法优化神经网络流程图

3 实验设计与结果分析

该动态补偿模型取训练次数为500，学习率定为0.002，训练的理想化目标定为0.03。为避免输入量相差过大导致预测误差过大进而影响实际结果，训练的初始阶段就应对所有样本数据进行归一化处理。数据预处理完成后，根据正交实验L18（27），将前三次实验所得的数据作为训练样本，再针对实际结果验证模型的有效性，可随机采集270组结果数据作为测量样本。随机选取50组动态误差参数经模糊神经网络补偿效果如图6所示。

图6 （a）和图6（b）为最大定位误差和残余定位误差补偿效果图，因为6个关节转角值在补偿时独立、随机且相互没有耦合，因此在做结果分析中仅以一个关节的补偿效果为例，即图6（c）所示。

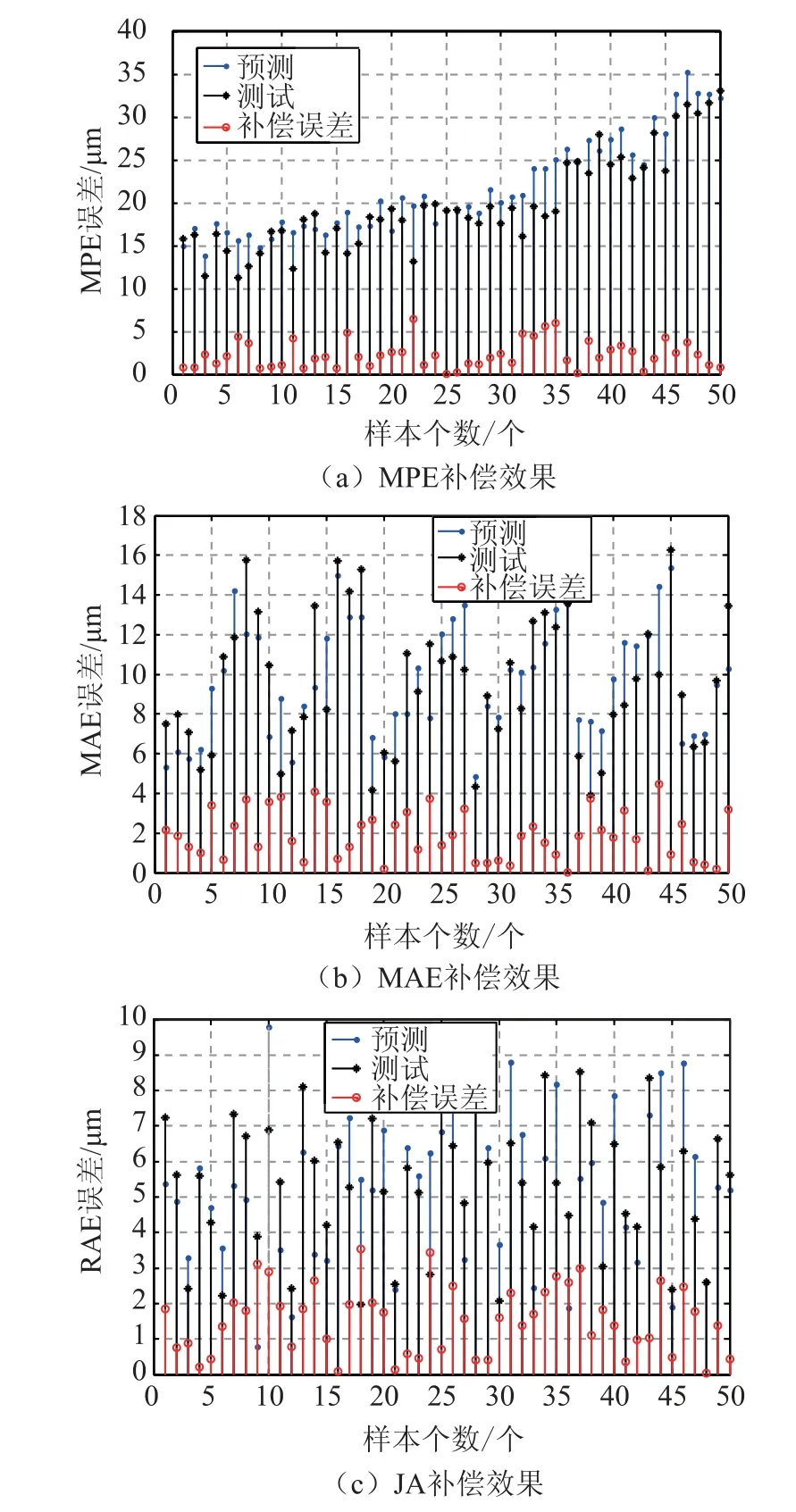
图6 动态误差参数模糊神经网络补偿效果

图6 中的蓝色点表示将样本数据中的输入数据导入动态误差模型后计算出的不同组合下动态误差的预测值；与样本数据作比较得到补偿误差，用红色点表示；再计算出测量样本输出数据补偿前的误差值，用黑色点表示。观察图6发现，预测值与测量值契合度很高，3幅图像的最大预测误差均小于6.3μm，异值出现的概率分别为2%，0%和0%（以±5μm为界），所以基于该预测值是切实可行的。同时用测量值和补偿后误差值之间的差与补偿前的测量值相比，即可得出该模型的误差补偿效果，如表1所示。由表1可知融合了模拟退火算法的模糊神经网络建立的动态误差参数模型具有良好的补偿效果。

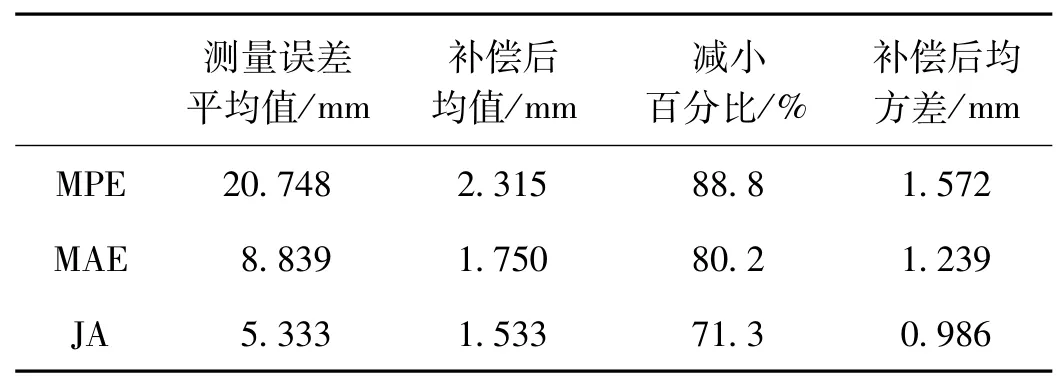
表1 SA-T-S模糊神经网络模型误差对比

实验结果表明，经模型补偿后动态过程误差分别减小了88.8%，80.2%，71.3%，证明该模型能够有效提高测量机的动态测量准确度，可为工业现场提高测量效率提供有力保障。

4 结论

1）本文讨论了关节臂式坐标测量机结果误差的众多影响因素中最主要的三个部分，即热变形误差、测量力误差与角度编码误差，并分别进行分析。

2）针对关节臂式坐标测量机动态误差参数的三个主要影响因子进行分析，即最大定位误差（MPE）、残余定位误差（RPE）和关节转角值（JA），采用正交实验探究了各个影响因素对3项动态误差参数的影响程度，为建立动态误差补偿模型奠定了基础。

3）将T-S模糊神经网络与模拟退火算法相结合，应用于三坐标测量机动态测量过程误差补偿，以3个影响因子为输入向量，3项动态误差参数作为输出建立动态误差模糊神经网络模型，经实验证明该模型具备良好的补偿效果，拓展了关节臂式测量机动态误差补偿技术，为提高关节臂式测量机动态准确度与测量效率提供了保障。