基于改进烟花算法的传感器动态特性补偿方法研究

郑德智，吴钧明，樊尚春

（1.北京航空航天大学前沿科学技术创新研究院，北京100191；2.北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引言

现代企业生产与科学研究对传感器的测试精度与测试环境要求越来越高，尤其是在动态测量领域，现有的传感器动态性能已不能满足实际测试需求，因此，进行了大量的改善传感器动态特性的研究工作。目前，改善传感器动态特性的途径主要有两种：一是改变传感器的结构和设计参数；二是从算法角度对传感器进行动态补偿。受限于材料、工艺及生产技术水平，目前动态补偿方式是改善传感器动态特性的主要研究方向［1］。

在改善传感器动态特性研究过程中，涌现出许多优秀的补偿动态算法，如零极点配置方法［2-3］、反卷积法［4］、神经网络法等［1，5-6］。随着群体智能算法的不断深入研究应用，也有部分研究学者将群体智能方法应用于动态补偿的研究中，其中的烟花算法（Fireworks Algorithm）具有机理简单、精度高、收敛快、不易陷入局部最优值等优点［7］，被广泛应用于不同类型问题的优化求解中，且取得较好的效果。由于烟花算法应用在传感器动态补偿时存在一些问题，使其不能取得相对理想的补偿效果。本文在标准的烟花算法基础上进行研究改进，并将其应用于传感器的动态补偿中，以改善传感器的动态性能，提高传感器动态测试的精度。

1 烟花算法传感器动态补偿原理

通常，传感器系统是低通特性，传感器系统的有效通频带（对数幅频特性曲线上±3 dB幅值内所对应频率范围）没有覆盖输入信号的高频部分，高频信号的幅值分量会有所衰减，且频率越高的信号，衰减得越严重，导致输出信号波形出现失真现象。静态测试过程中，低频信号为测试信号的主要组成部分，可以获得较高的测试精度，但在动态测试过程中，高频信号为测试信号的主要组成部分，因此需要对传感器进行动态补偿，即拓宽传感器的通频带。经动态补偿后的传感器测试系统整体呈低通特性，但是相比原传感器系统，其通频带得到了有效的拓宽，如图1所示，因此可以有效减小因高频信号衰减所造成的动态响应误差且提升动态响应时间。

图1 传感器动态补偿前后系统的通频带示意图

传感器动态补偿原理是在传感器系统之后串接一个补偿器，形成一个单位复合系统，拓宽原传感器的通频带，减少因高频信号衰减引起的动态测试误差，使得补偿后的系统输出信号尽可能接近传感器的输入信号。传感器动态补偿原理如图2所示，其中，u（n）为传感器输入信号；y（n）为传感器输出信号；u′（n）为补偿后输出信号。

图2 传感器动态补偿原理示意图

以差分方程形式描述补偿器系统，补偿器的输入输出差分方程为

式中：A（z）与B（z）分别为补偿器模型输入项与输出项的系数。

补偿器系统H（z）表示为

图3 给出基于改进烟花算法的传感器动态补偿的原理图，将传感器输出信号y（n）作为补偿器系统的输入信号，r（n）为参考模型的输出信号，u′（n）为补偿后的输出信号。a1，a2…an，b1，b2…bn为补偿器模型参数。采用改进的烟花算法不断优化调整补偿滤波器模型参数，获得相对小的适应度值，即补偿后的输出与参考模型输出误差达到一个较小的值。根据获取的补偿器模型参数构建符合要求的补偿滤波器，串接在原传感器系统之后，达到改善其动态特性的目的。

图3 基于改进烟花算法的传感器动态补偿的原理图

2 基于烟花算法的补偿算法

2.1 烟花算法的算法流程

烟花算法是谭营等人受到烟花在夜空中爆炸产生火花点亮夜空现象的启发而提出的算法，其核心思想简单，但具体实现相对复杂［8］。烟花算法尽管提出时间较晚，但经过众多研究学者的不懈努力，近年来已有了不少的改进方案和较为全面的应用。

烟花算法流程图如图4所示。

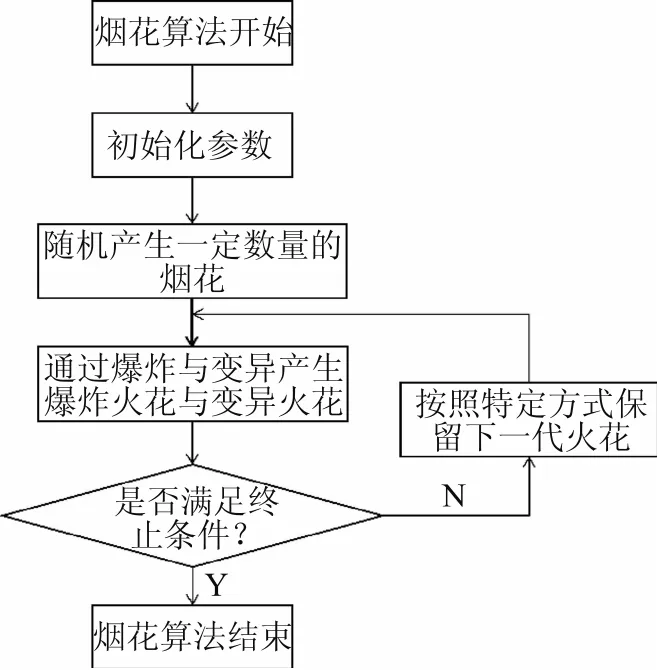
图4 烟花算法流程图

烟花算法主要包括以下几个步骤：①初始化参数，包括最大迭代次数、爆炸火花的数量、变异火花的数量、火花维度大小、每次迭代保留的火花数量等；②在求解区域随机产生一定数量的烟花，每一个烟花都代表着最优化问题的一个可行解；③根据适应度函数计算每一个烟花的亮度适应度值，根据适应度值的大小，区别不同火花的亮度。适应度越好，即火花越亮，使会在较小的求解区域内产生更多的火花；而亮度越低的火花会在较大的求解区域内产生较少的火花。即较差位置大范围少量搜索，较好位置小范围大量搜索，不从众；④产生的爆炸火花与高斯变异火花中按照相应的策略保留一定数量的火花进入下一轮迭代搜索；⑤判断是否达到最大迭代次数或者当前最佳火花的适应度值是否低于设定值，如果满足条件即停止迭代搜索，否则进入下一轮迭代搜索。

2.2 烟花算法的动态补偿应用与改进

2.2.1 火花的爆炸与变异改进

在标准的烟花算法中，根据每个烟花的适应度值，可以计算其爆炸半径R（求解搜索区域的大小）以及产生的爆炸火花数目N，以最佳适应度值为最小值的优化问题为例，其计算公式为

式中：Vi为第i个烟花的适应度值；Vmin为烟花种群中最小的适应度值；Vmax为烟花种群中最大的适应度值；Rmax为最大的爆炸半径；Nmax为爆炸火花数目的最大值；ζ为一个极小的值，用于避免分母为零的情况。

传感器的动态补偿器的最优参数求解时，因存在反馈环节，会出现某些火花的适应度值异常大的情况，按照上述的方式进行计算，会出现暗的火花爆炸半径接近最大爆炸半径，且产生的爆炸火花数量极少。而较亮的火花爆炸半径趋于无穷小，且产生较多的爆炸火花，会导致大部分的求解区域没得到有效的勘探，为避免类似情况的发生，可以限制种群中最大的适应度值的方式，如果种群中某个火花的适应度值高于限定值Vlimit，则令其等于限定值，即

烟花爆炸会产生两种火花：一种是正常爆炸火花；另外一种是高斯变异火花。每个火花在爆炸后都会产生一定数量的正常火花，而爆炸火花存在一定几率发生变异生成高斯变异火花。从爆炸火花中随机选择一定数量的火花进行变异操作，具体流程如下，对于进行变异的火花，首先随机选择k个维度数量进行变异（k≥1且k≤火花最大维度L）。对于第i个火花的某一个被选择的维度h执行高斯变异操作如下

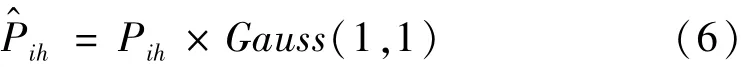
式中：pih为第i个火花的位置坐标的h维度的值；Gauss（1，1）表示均值为1，方差为1的高斯分布。

2.2.2 火花选择策略改进

烟花算法中，每一代产生的爆炸火花与高斯变异火花中只能保留一定数量的火花，以避免种群数量膨胀导致计算资源崩溃。火花的保留采用的是轮盘赌的方式，对于每个候选火花pi，其被选择保留的概率P（pi）计算公式为

式中：R（pi）为第i个火花pi与其他当代火花之间距离总和；sum为除火花pi外的所有火花个体集合。

该方法虽然可以减少求解区相对集中的个体的选择的概率，但是计算量庞大，在实际操作时，浮点数的运算会占用较大的计算资源，而采用上述方式进行操作，会占用烟花算法优化求解的大量时间。本文改进的方案是采用一种适者生存的思想对选择火花策略进行改进，对所有火花的适应度值按照从小到大进行排序，选择占保留火星总数的1/10至1/5的前n个火花保留到下一代，其余的火花则采用随机选择的方式进行选取，此方式既可以保留当前种群中适应度较好的火花，可以对适应度较好的火花区域进行更深一步搜索，而随机选择的一部分则使其具有更好的探索能力。

2.2.3 火花适应度函数改进

烟花算法中，根据计算每一个火花个体的适应度值，在N个维度的空间中，不断迭代搜索更新当前最优火花的位置信息pbest=［a0，a1…aN］。烟花算法的适应度函数一般选择均方误差的形式，即

式中：V为适应度值；N为数据长度；u′（n）为补偿后的输出；r（n）阶跃输入的模型参考输出。

按照以上的方式，在对传感器进行补偿时，有可能会出现瞬时大超调的现象，如图5所示。

瞬时大超调的现象的出现是由于烟花算法在迭代搜索时是朝着适应度值V→0的趋势进行的，占据时间比例更大的稳态环节成为影响适应度值的主导部分，而维持时间较短的瞬态环节对适应度值的计算影响较小，但实际测试过程中，即使维持时间很短，但这种较大瞬态的测试误差也有可能对测试造成较大影响。因此本文采用了一种可调整的适应度函数为

图5 动态补偿瞬时大超调现象

式中：w1，w2为权重系数；δ为超调量。

其中w1主要影响稳态精度，而w2主要影响超调量的大小，在实际测试过程中，对不同的传感器，即不同的优化求解模型，w1，w2的影响有所不同，在实际过程中可根据多次实验测试得到合理的权重系数，以提高动态性能参量对适应度值计算的影响，避免瞬态大超调现象，同时获得相对较好的稳态输出。

2.3 仿真实验测试

常见的传感器多为高阶系统，而高阶系统通常可简化为二阶系统进行分析研究，因此本文对传感器的动态补偿研究采用二阶系统进行仿真分析。

其阶跃响应如图6所示，可以看出，原传感器系统稳态误差较小，但动态性能较差，单位阶跃响应稳态时间2 s左右（允许误差范围为±5%），超调量超过60%。

图6 传感器模型的阶跃响应

采用改进后的烟花算法对其进行动态补偿，首先选择补偿滤波器的阶数，理论上，动态补偿滤波器阶数越高，其补偿效果越好，但是阶数达到一定数量后，再增加补偿滤波器的阶数对补偿效果的改善并不明显。而一味增大滤波器的阶数，会带来额外的计算工作量，增加实现难度，综合考虑，补偿滤波器模型阶数选择四阶，构成的补偿滤波器系统传递函数为

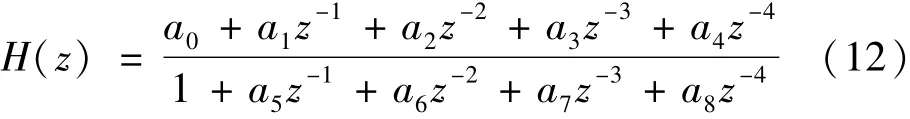
以传感器的测试输出信号为补偿器的输入，输入信号为参考输出，采用改进后的烟花算法进行补偿器参数优化求解，实验中，理论上火花数量越高在相同迭代次数下可获得更快的收敛速度，但实际上，火花数量到了一定值，其数量的影响不再显著，经过多次实验，选定迭代火花初始火花数量为1000，高斯变异火花为500，爆炸产生火花数量最大值为100000，迭代训练次数为500次，适应度值的权重系数w1，w2分别设定为0.7和0.3时，（经多次实验，一般在训练次数达到300～400次时，适应度值逼近最优解，而权重系数w1，w2则是通过多个不同传感器模型多次实验确定的一个合理参数）得到的补偿滤波器为

将该动态补偿器与原系统串接，形成单位复合系统I（z）

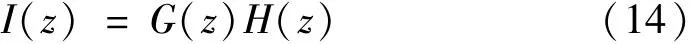
其单位阶跃响应结果如图7所示，动态补偿前后系统部分动态指标如表1所示。

图7 传感器动态补偿结果

表1 动态补偿前后系统部分动态指标

由对该二阶传感器系统的仿真结果可知，动态补偿后系统的超调量明显减少，其稳态调节时间大幅度减少，原传感器系统的动态性能得到了一定程度上的提升，同时验证了该补偿算法的可行性。

3 实验验证

为进一步验证算法的补偿效果，将用改进前后的烟花算法对科氏质量流量计变送器的动态性能进行提高。科氏质量流量计是一种基于谐振原理和科氏效应的直接质量流量传感器，由传感器的基本敏感单元和二次仪表组合而成，测量准确度高，测量流体范围广，是当前发展最为迅速的流量计之一［9-10］。现阶段对科氏质量流量计的研究主要以静态特性为主，但随着对流量动态测量准确度要求的提高，其动态性能变得至关重要。根据现有的研究表明，限制科氏质量流量计动态响应速度的是二次仪表，即变送器部分［11］。

在实际测试过程中，科氏质量流量计的敏感单元部分作用是将测量管腔中流体的质量流量转换为两路具有相位差的正弦信号，变送器部分对这两路信号进行运算处理，求取其相位差。被测流体的质量流量与该相位差具有一定比例关系。本文由于只考虑对变送器进行动态补偿，因此使用模拟信号源来提供两路相位差可调的正弦信号，用于模拟流量阶跃变化信号。利用模拟信号源对模拟生成不同相位差的正弦信号，获取变送器的等效阶跃输入信号和输出信号的实测数据如图8所示。

图8 科氏质量流量计输入输出数据

采用改进前后的烟花算法对其进行动态补偿对比分析，补偿滤波器模型阶数选择二阶，在获取的科氏质量流量计变送器的测试数据之后，通过烟花算法获取补偿器的系数。实验时，设置好所有的训练参数后，同时采用改进前后的烟花算法对数据进行迭代训练，500次迭代训练后得到的补偿器的模型参数。其中标准的烟花算法由于采用轮盘赌的选择概率方式，500迭代运算耗时超过7 h，得到最终适应度值为0.439；而改进后的烟花算法同样参数设定情况下，500迭代运算耗时仅63 min，得到最终适应度值为0.0538。

经试验，标准的烟花算法模型为

改进后的烟花算法模型为

采用差分方程形式，动态补偿滤波器可表示为

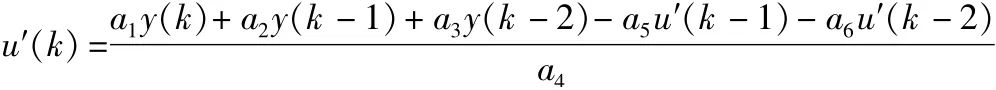
将得到的动态补偿滤波器编程写入硬件系统中，运行算法程序从存储空间中调用数据进行实时解算以及动态补偿滤波，将实时采集的科氏质量流量计变送器输出与实时动态补偿的输出数据通过串口读入计算机中，然后分析计算补偿前后的阶跃响应参数，动态补偿前后结果如图9、图10所示。

图9 动态补偿输出效果

图10 动态补偿输出效果局部放大图

由实验结果来看，经过改进前后的烟花算法动态补偿后，科氏质量流量计变送器的输出的数据曲线基本与阶跃响应输入数据曲线相贴合，但对比改进前后的烟花算法补偿结果可以发现，经标准烟花算法补偿后，其响应时间（误差±2%）由0.718 s缩短至0.056 s，但同时存在着5.4%的局部瞬时超调。而改进后的烟花算法在训练耗时上有了明显的减少，其补偿后的响应时间（误差±2%）由0.718s缩短至0.08 s，且不存在局部瞬时超调的情况，在保证稳态精度的同时极大提高了变送器的响应速度，动态性能有了大幅度的提升，进一步验证了改进后算法的可行性。

4 结论

为了改善传感器动态性能，尝试将烟花算法用于传感器的动态补偿研究。根据所获取的传感器的测试数据，使用改进的烟花算法对补偿滤波器进行优化求解。将该方法应用于科氏质量流量计变送器的动态补偿，由实验结果可知，该方法达到98%稳态输出的时间为0.08 s，远小于补偿前的0.718 s，同时补偿后稳态准确度提升，误差保持在0.5%以内。采用改进后的烟花算法的动态补偿方式，可以有效拓宽传感器测试系统的工作带宽，改善其动态特性，进而提高传感器的响应速度与计量准确度。