求素数新法的研究

李 高，史万红

(1.山西大同大学 数学与计算机科学学院，山西 大同 037007；2.尚义县红土梁镇中心小学，河北 尚义 075760)

人们对整数性质的研究开始很早,对数的性质的研究也越来越深入和精细,并逐渐形成了数学的一个分支——数论。

定义：对于一个整数只有1和本身是它的约数，则该整数称为质数或素数。

素数尽管人们耳熟能详，它的出现使一个个貌似简单的问题，如算术基本定理、素数定理、素数等差数列、哥德巴赫猜想、黎曼猜想、孪生质数猜想等，令多少代数学家一生追寻与探索，且一直困惑着，而终身无果。

早在公元前6世纪,古希腊的数学家毕达哥拉斯和他的学生研究了数的整除性问题。公元前3世纪,欧几里得就提出了用辗转相除法求最大公约数的方法。中国在整数性质方面的研究也比较早，约在公元前100年到公元100年间成书的《九章算术》里讲到约分,方法是“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求共等也,以等数约之”[1]。就是分子、分母都是偶数时,应该都用2除；如果不都是偶数，那么用辗转相减的方法,从较大的数里减去较小的数,最后得到一个余数和减数相等,这就是所求的最大公约数。这种辗转相减求最大公约数的方法和欧几里得算法异曲同工,理论上是完全一致的。

1 素数的无穷性

素数的独特形式吸引着众多数学家，关于素数有无穷多个问题,早在公元前300多年,就被古希腊数学家欧几里得在《几何原本》中证明了。但是,由于数越大,发现素数就越困难。因此,目前人类已知的素数还是为数有限的。

17世纪法国费尔马(Pierrede Fermat)曾经猜测形如22n+1(n>0)的数都是质数。其实这个猜测是错误的，例如,当n=5时,21+1=22并不是质数。但是费尔马的猜测却给了后人很大的启发,以后发现的大质数都与这个公式相近。1876年数学家卢卡斯发现了当时最大的质数2127-1,是37位数,这个纪录保持了75年,直到1951年,由于计算机的出现,才发现具有7个数位的更大质数180×(2127-1)2+1。此后,纪录不断被刷新,1979年美国劳伦斯·利莫费尔实验室的两位计算机专家发现了目前最大的质数24497-1,这个数是1395位数[2]。

17世纪法国数学家马林·梅森猜测形如2P-1的正整数都是素数，(其中P是素数)。若2P-1是素数，则称为梅森素数，简称梅森数。当P=2、3、5、7时，2P-1都是素数，但P=11时，211-1=2047=23×89不是素数，是否存在无穷多个梅森素数是数论中未解决的难题之一。

2016年1月美国柯蒂斯·库珀发现世界上迄今为止最大的梅森质数257885161-1，长达2 233万位，如果用普通字号将它打印出来长度将超过65 km。至今累计发现49个梅森素数，人们在寻找梅森质数的同时，对其重要性质——分布规律的研究也一直在进行着。英、法、德、美等国的数学家都曾分别给出过有关梅森质数分布的猜测，但都以近似表达式给出，与实际情况的接近程度均难如人意。中国数学家、语言学家周海中是这方面研究的领先者，他于1992年首次给出了梅森质数分布的精确表达式。这一成果后来被国际上命名为“周氏猜想”。

素数貌似简单，但研究难度却极大。由于梅森素数珍奇而迷人，它被人们誉为“数论中的钻石”。这种素数历来是数论研究的一项重要内容，众多科学家认为梅森素数的研究成果是一个国家科技水平的体现，不仅推动了数论的研究，而且促进了计算机技术、程序设计等技术的发展。一些素数已经被用于加密和其他实际应用任务，因此成为当今科学探索的热点和难点之一。威斯康辛州立大学(University of Wisconsin)的数学家Jordan Ellenberg就曾说：“发现一个梅森素数就像是在干草堆里找一根针那么困难。这项发现在计算机工程领域的价值要远大于数学领域的价值。”

2 埃拉托斯特尼筛

2.1 埃拉托斯特尼筛法

最初的若干素数为2、3、5、7、11,13、17,19、23、31、37、41、43…，如果N不太大,求小于N的素数并非难事。

公元前3世纪,希腊学者埃拉托斯特尼找到一种求1 000以内质数的方法:依次写出2到1 000的自然数,第一个数2是质数,把2留下,把所有2的倍数即偶数划去；2后面第一个未划去的数是3,而3是质数,把它留下,再把剩下的数中所有3的倍数都划去；3后面第一个未划去的数是5，而5是质数,把它留下,再把剩下的数中所有5的倍数都划去。这样继续下去划到37以前的一个质数为止,最后留下的数就组成了1 000以内的质数表。此法称为求素数的埃拉托斯特尼筛法。

2.2 埃拉托斯特尼筛由来

因为希腊人是把数写在涂腊的板上,每要划去一个数,就在上面记以小点,寻求质数的工作完毕后,这许多小点就象一个筛子，所以就把埃拉托斯特尼的方法叫做“埃拉托斯特尼筛”,简称“筛法”。

另一种解释是当时的数写在纸草上,每要划去一个数,就把这个数挖去,寻求质数的工作完毕后,这有许多孔的纸草就象一个筛子。

2.3 判断一个正整数是素数的方法

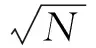
3 一种新的求素数的方法

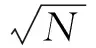
第一步：首先素数3自乘得9,则5和9之间的奇数7必为素数。

因为,如果5和9之间的奇数7不是素数的话,那么就应该有比5和3还小的素数自乘、相乘或和3、5相乘的积中包含7,但这样的素数显然是不存在的，故5和9之间的奇数7必为素数。因此，比9小的所有素数3、5、7已求得。

第二步：求比9大的素数

在3、5、7的自乘或互乘的乘积中,比9大的最小数是3×5=15,则9和15间的奇数11、13必为素数。因此，比15小的所有素数2、3、5、7、11、13已求得。

第三步：求比15大的素数

在3、5、7、11、13的自乘或互乘的乘积中,比15大的最小数是3×7=21，则15和21之间的奇数17、19必为素数，因此，比21小的所有素数2、3、5、7、11、13、17、19已求得。

第四步：求比21大的素数

在3、5、7、11、13、17、19的自乘或互乘的乘积中,比21大的最小数是52=25,于是21和25之间的奇数23必为素数。又33=27是紧挨着25的奇数,比25小的素数,当然比27小的素数也就求得了，即比21小的所有素数2、3、5、7、11、13、17、19、23已求得。

第五步：求比27大的素数

在3、5、7、11、13、17、19、23的自乘或互乘的乘积中,比27大的最小数是3×11=33,于是27和33之间的奇数29、31必为素数。因此，比33小的所有素数2、3、5、7、11、13、17、19、23、29、31已求得。

…… …… …… ……

继续不断地照此进行下去,就能一个不漏地求得越来越大的素数。

这个过程可无限进行下去，其过程如下